涡轮增压器转子模态测试研究

金艳秋

涡轮增压器转子模态测试研究

金艳秋

（辽宁省交通高等专科学校 汽车工程系，辽宁 沈阳 110122）

采用锤击法对某涡轮增压器转子进行模态测试，并对其自由模态进行模态拟合和模态验证．在采集频率范围内相干系数趋于1，频响函数FRF清晰，且激励信号的功率谱密度衰减平稳，无骤变；通过LMS测试系统直接对9个测点的频响函数进行模态拟合，拟合曲线与采集数据误差低于1%；涡轮增压器转子前两阶模态频率测试，1阶弯曲频率1081．7Hz，2阶弯曲频率3565．6Hz．表明测试得到涡轮增压器转子前两阶固有频率和模态振型具有较高的测试精度和可信度．对有限元数值计算结果进行了模态频率和振型校核，误差满足工程应用需求．

涡轮增压器转子；固有频率；模态振型；模态验证

涡轮增压是发动机实现节能减排、日益小型化的关键技术之一．它利用发动机排出废气驱动涡轮机膨胀做功，带动与其同轴的压气机旋转，压缩进空气实现增压的目的．随着发动机排量的减小，强化程度的不断提高，涡轮增压器向着高压比、高效率、高可靠性的方向发展，同时其转速最高可达20～30万转每分．［1］因此，涡轮增压器转子部件工作的稳定性和可靠性越来越备受关注．

如图1所示，涡轮增压器转子由涡轮转轴、叶轮、轴端螺母以及轴封套等组成，叶轮大径56mm，涡轮大径48mm，转轴直径7mm，总长130mm．涡轮与转轴通常采用摩擦焊或电子束焊接一体，叶轮和轴封套穿在转轴上，再由轴端螺母锁紧，在涡轮增压器工作过程中，涡轮带动叶轮做功．对涡轮增压器高速旋转转子的固有特性进行研究分析，是对涡轮增压器转子－支承系统进行动力学设计分析的第一步，对转子－支承系统工作的稳定性和可靠性有着重要影响．［2］本文对某涡轮增压器转子进行模态测试研究，并与有限元计算分析结果进行对比，完成计算方法的校核．

图1 涡轮增压器转子组件

1 测试装置

试验采用多点锤击单点拾振的测试方法，激励采用PCB力锤，LMS Test．Lab动态信号采集分析系统，振动加速度传感器粘贴于转子中部敲击点5处，避开可能的转子振型节点处（如图2所示）．［3］组合安装好的涡轮增压器转子用弹性绳悬挂，悬挂长度不小于0．5 m，并保证被测件水平状态．用力锤对转子作竖直方向敲击，从而测得转子自由状态下的频率和振型．

模态是机械与结构固有的振动特性，每一阶模态都具有特定的固有频率和模态振型．通过模态分析可以得到结构体在某一频率范围内各阶主要模态的特性．模态参数识别方法大体上可分为时域法和频域法两类．其中频域法是使用较广泛和成熟的方法［4］，也是本文采用的方法．

敲击点位置的选取要考虑到转子自身的结构，是否便于力锤敲击，敲击点数的选择则要求能够准确表现转子前两阶弯曲模态振型，若取点过少则会造成模态振型失真．因此，本文对于此涡轮增压器转子，沿转子轴向取9个敲击点比较合理，转子模型及测点分布见图3，加速度传感器固定在第5点，模态分析仪的采样频率取为6400Hz．

图2 测试系统

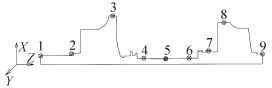
图3 转子模型与测点分布

2 测试原理

将采集的各通道时域信号滤波后进行FFT变换，可得到频域信号．如果把系统的激振力f（t）看作输入，振动的位移响应x（t）看作输出，则系统的传递函数［5］为

对多自由度系统，其在任意激振力下的运动方程［6］为

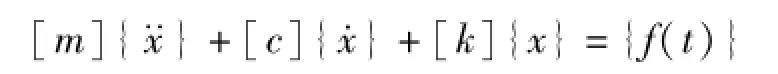
对方程作拉普拉斯变换，并令所有坐标的初值位移和初始速度为零，则

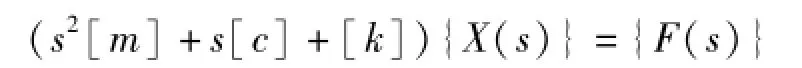
其中，［m］为质量矩阵，［k］为刚度系数矩阵，［c］为阻尼系数矩阵，X（s）和F（s）分别为x（t）和f（t）的拉普拉斯变换．［7］

通过变换可以得到各自由度下的频响函数．仅以第1点为例进行说明，当相干系数、激励信号功率谱密度和频响函数输出三者同时满足相应评判条件时，则表明力锤选择合适．如图4，第1敲击点的频响函数及相干曲线是一典型的频响函数幅值、相干系数及激励信号功率谱密度（PSD）曲线图．在采集频率范围内相干系数是趋于1的，频响函数FRF清晰，且激励信号的功率谱密度衰减平稳，无骤变，表明力锤选择合理．在频响函数的基础上，通过最小二乘法可以得出模态的参数．［8］

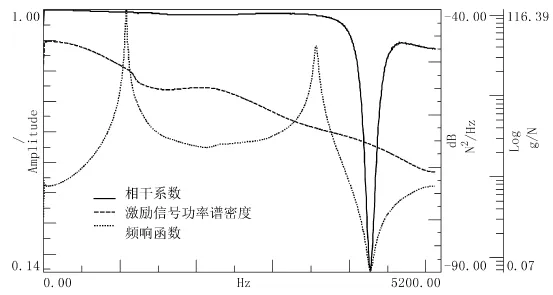
图4 第1敲击点的频响函数及相干曲线图

3 测试结果评判

9个测点按编号顺序依次完成敲击试验，每个测点敲击5次取平均，开启采集系统自动判断功能，剔除双击、超载等错误数据．模态测试结果必须进行模态拟合和模态验证，确保测试结果合理有效．

3．1 相干系数

对涡轮增压转子这种比较简单的转子进行模态测试，一般要求大部分敲击点共振频率处的相干系数要大于0．9，各个测点模态拟合相关系数如表1和图5所示，前7个敲击点的相干系数在共振频率处全部满足要求，敲击点8和9的相干系数在二阶模态频率处分别为0．72和0．84，略低于0．9．因此总体看来，相干系数基本满足要求，测试过程合理．

图5 9各个敲击点的相干系数

表1 各个测点模态拟合相干系数

3．2 模态拟合

LMS测试系统直接对9个测点的频响函数进行模态拟合（Modal Synthesis），9个点的拟合误差统计如表2所示，拟合曲线与采集数据误差均低于1%．如图6所示，第1敲击点模态拟合得到的频响函数曲线与实测结果的幅值和相位都具有很高的一致性．表明测试结果准确可信．

表2 各个测点模态拟合误差

图6 敲击点1的频响函数曲线

3．3 模态验证

涡轮增压器转子前两阶模态频率测试结果如表3所示，1阶弯曲频率1081．7Hz，2阶弯曲频率3565．6Hz，相应的振型见图7．因为一是转子的工作转速最高250000r／min（4167Hz），更高的阶次频率已远超过工作范围，结合实际应用应重点关注前两阶模态频率；二是不同力锤适用不同的频率测试范围，频率由低到高依次为：橡胶＜金属＋橡胶＜金属．本试验选用橡胶＋金属的力锤，通过多方面分析表明结果合理，而其适用的频率范围也不能达到更高阶的需求．所以对测试结果进行模态验证分析不考虑更高阶次．

表3 模态测试结果及验证

表4 模态置信判据（MAC）

图7 前2阶弯曲模态振型测试结果

模态模型的参数为固有频率、阻尼比、模态振型和模态参预因子．文章采用模态置信判据（MAC）、模态相位共线性（MPC）和平均相位偏差（MPD）来验证模态模型的精度．［9］响应的模态置信判据（MAC）表示模态的可信程度，同时检验模态振型被质量加权时的正交性．［10］

比较相同试验数据按不同的模态参数估计方法得到的模态振型，对于相似的模态振型而言，MAC的值应接近于100%．此涡轮增压器转子模态测试MAC如表4所示，矩阵对角MAC为100%，说明2阶模态为主模态．

对于实正则模态，模态相位共线性（MPC）指数应很高，接近100%．若MPC指数有低值，表明在一定程度上是复模态，其原因或是试验结构上存在局部的阻尼元件，或是有不良的测量或分析处理．平均相位偏差（MPD）指数指示出模态振型在相位上的分散程度，对于实正则模态，MPD值应很小．测试系统通过数据处理分析得出前两阶模态的相位共线性指数．该测试的MPC指数大于95%，较高；MPD指数低于15%，说明测试方法及数据处理合理，分散度低．

在测点5处粘贴传感器后，附加质量会引起模态频率的降低，模态超复性（MOV）反映了固有频率确实降低的这种测点所占的加权百分比．在测点5处粘贴传感器主要降低了该涡轮增压器转子的2阶模态频率．

4 转子固有频率计算

转子自由模态的计算采用有限元计算方法，建立涡轮增压器转子实体三维模型，进行网格划分，各部件内孔与转轴绑定连接，侧面定义为接触面．有限元分析计算结果见表5和图8．

对比试验与计算结果可以看出，计算和测量的模态振型一致，计算得到的固有频率较实际测量值略微偏高，误差约5%，可能是由于传感器附加质量提高了涡轮增压器转子刚度所致，但属于工程计算可接受范围内．表明验证试验方法和结果合理有效．

表5 涡轮增压器转子模态计算结果

图8 前2阶弯曲模态振型计算结果

5 结论

1）采用锤击法测试得到的涡轮增压器转子自由模态的前两阶固有频率分别为1081．7Hz和3565．6Hz．

2）对测试结果进行模态验证分析，表明测试结果精度高，准确可信．

3）涡轮增压器转子有限元数值计算模态频率和振型与测试结果基本一致，表明验证试验方法和结果合理有效．

4）传感器粘贴测点5与2阶弯曲模态振型节点接近，故可调整传感器粘贴位置，以提高2阶弯曲模态的测试精度．

［1］ CHOUKSEY M，DUTT J K，MODAK S V．Modal analysis of rotor－shaft system under the influence of rotor－shaft material damping and fluid film forces［J］．Mechanical＆Machine Theory，2012，48（1）：81－93．

［2］ 钟一谔，何衍宗，王 正，等．转子动力学［M］．北京：清华大学出版社，1987．

［3］ 比利时LMS国际公司北京代表处．LMS Test．Lab中文操作指南－Impact锤激发模态测试与分析［M／OL］．北京：比利时LMS国际公司北京代表处，2009：3－18［2016－06－13］．http：／／http：／／max．book118．com／html／2015／1107／28795083．shtm．

［4］ LMS振动／噪声测试与分析系统理论基础［M］．刘馥清，编译．北京：机械工业出版社，2000．

［5］ 朱大鑫．涡轮增压与涡轮增压器［M］．北京：机械工业出版社，1992．

［6］ CHEN W J．Rotor dynamics and bearing design of turbocharge［J］．Mechanical Systems＆Signal Processing，2012，29（5）：77－89．

［7］ 田文凯，房桐毅，王澄宇，等．涡轮增压器转子系统的模态分析和临界转速计算［J］．柴油机，2014，36（2）：27－30．

［8］ 杨永锋，任兴民，徐 斌．国外转子动力学研究综述究［J］．机械科学与技术，2011，30（10）：1775－1780．

［9］ 叶帅奇，方 沂，王旭龙，等．新型机械增压器转子系统模态分析［J］．机械工程师，2013（8）：142－144．

［10］ 杨 帆，胡国良，黄幼林．增压器涡轮叶片设计及模态分析［J］．内燃机与配件，2012（1）：4－5，12．

Testing Research on the Mode of Turbocharger Rotor

JIN Yanqiu
（Department of Automotive Engineering，Liaoning Provincial College of Communications，Liaoning 110122，China）

The modal test was carried out by impact method while the rotor of the turbocharger free modal validation proceeded．Within the scope of the sampling frequency correlation coefficient tends to 1；the frequency response function FRF is clear；excitation signal power spectral density of attenuation is smooth and not change．Through LMS test system directly modal fitting frequency response function of nine points，the error of fitting curve and data is less than 1%．The first two order modal frequency rotor of the turbocharger test，1 order bending frequency is 1081．7Hz while 2 order bending frequency is 3565．6Hz．The results indicated that the first two order natural fre⁃quency and modal vibration mode of the turbocharger rotor were both reliable and accurate．Compared to the natural frequency and mode shape results by numerical analysis，they were consistent and the error was acceptability．

turbocharger rotor；natural frequency；mode shape；modal validation

TK403

A

2095－4476（2017）05－0024－05

（责任编辑：饶 超）

2016－12－22；

2017－02－22

沈阳市科协科技创新智库项目（2016－45C）

金艳秋（1983— ），女，辽宁凌源人，辽宁省交通高等专科学校汽车工程系讲师．