雅可比迭代法求解稀疏矩阵

江苏省南京林业大学理学院信息与计算科学系 钱耀飞

雅可比迭代法求解稀疏矩阵

江苏省南京林业大学理学院信息与计算科学系 钱耀飞

本文在求解大型稀疏线性代数方程组时，通过Mathematica软件，判断雅可比迭代法的谱半径和迭代精度达到的迭代次数。

雅可比迭代；稀疏矩阵；谱半径；迭代次数

给定n阶线性代数方程组Ax=b，其中：

当n=5，10，20，50，100，200时，判断雅可比迭代法的谱半径和迭代精度达到时的迭代次数。

对于本题中给定的三对角线性方程组Ax=b，雅可比迭代法的迭代格式为：

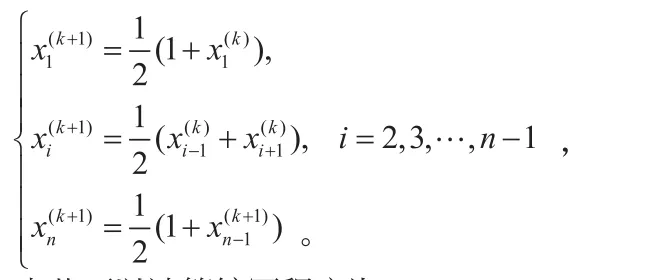
由此可以计算编写程序为：

n=10；

b=ConstantArray[0，n]；

b[[1]]=1；b[[n]]=1；

x0=ConstantArray[0，n]；

x1=x0；err=1；k=0；

While[err＞10^(-8)&&k＜25000，

x1[[1]]=(b[[1]]+x0[[2]])/2；

Do[x1[[i]]=(b[[i]]+x0[[i-1]]+x0[[i+1]])/2，{i，2，n-1}]；

x1[[n]]=(b[[n]]+x0[[n-1]])/2；

err=Max[Abs[x1-x0]]；

x0=x1；

k++]；Print[“k=”，k，”err=”，N[err]]；N[x1]

k=375err=9.74235＊10^-9(＊迭代次数以此迭代的误差＊)

{1.，1.，1.，1.，1.，1.，1.，1.，1.，1.}（＊求得的解＊）

我们可以看到，当n=10时，雅可比迭代法在迭代了k=375次后，达到了题目给的精度要求。我们假设A=D-L-U，其中D，-L，-U分别为A的对角线元素，严格下三角部分和严格上三角部分，则可以得到雅可比迭代法的迭代矩阵为J=D-1(L+D)。

给出下面的程序，计算上述雅可比迭代的迭代矩阵的谱半径。

n=10；

A=SparseArray[{Band[{2，1}]-＞-1，Band[{1，1}]-＞2，

Band[{1，2}]-＞-1}，n]；

d=Diagonal[A]；

（＊构造矩阵A，对角线元素为2，下次和上次对角线元素均为-1＊）

Diag=DiagonalMatrix[d]；

（＊Diag表示构造的对角矩阵＊）

L=-A＊SparseArray[{i_，j_}/；j＜i-＞1，{n，n}]；

U=-A＊SparseArray[{i_，j_}/；j＞i-＞1，{n，n}]；

A==Diag-L-U(＊检验矩阵分解是否正确＊)

True(＊结果为True，说明矩阵分解是正确的＊)

J=Inverse[Diag].(L+U)；（＊计算雅可比迭代矩阵＊）

Max[Abs[Eigenvalues[N[J]]]]（＊计算雅可比迭代矩阵的谱半径＊）

0.959493

当n等于其他值时，雅可比方法的迭代次数和迭代矩阵谱半径如下表所示：

雅可比迭代法的迭代次数和迭代矩阵的谱半径与方程组阶数n的关系

?

由上表可知，当雅可比迭代法的迭代次数随着n的增大而急剧增加，误差也越来越小，原因在于迭代矩阵半径越来越小，接近于1。因此我们现在核心的问题就是减少谱半径，从而减少迭代的次数。

[1]李庆阳，王能超，易大义.数值分析[M].北京：清华大学出版社，2008.

[2]王同科，张东丽，王彩华.Mathematica与数值分析实验[M].北京：清华大学出版社，2011.

book=38,ebook=40