源于基础 深入思考——从椭圆焦点三角形谈起

山东省微山县第一中学(277600) 朱广军

源于基础 深入思考
——从椭圆焦点三角形谈起

山东省微山县第一中学(277600) 朱广军

一个顶点在椭圆上,另两个顶点为椭圆焦点的三角形叫椭圆的“焦点三角形”.与“焦点三角形”有关的问题可以综合地考查三角形中的正(余)弦定理、面积公式及圆锥曲线的定义和标准方程等知识.涉及焦点三角形面积、弦长问题多次出现在试题中,直接解答一般较复杂,若我们能合理而又灵活地运用椭圆的焦点三角形的面积公式、焦半径、焦点弦弦长公式,在解决这类有关问题时,可避免冗长的推理和运算,大大降低难度,从而使问题得以巧妙简单地解决.因此很有必要对椭圆的焦点三角形、焦半径、焦点弦弦长公式等问题进行系统地研究.

此结论在教学中重点讲到,此处不再证明,只给出举例应用

点评一般方法运用定义和勾股定理|PF1|2+|PF2|2=4,解得|PF1|·|PF2|=2,S△F1PF2=1.运用面积公式大大简化了运算过程.思考在结论1中,若已知∠PF1F2=θ,那么是否有类似的焦点三角形面积公式呢?经过推理证明得到以下结论.

(2)证明与(1)相仿,从略.

点评利用结论2,可以省略复杂的思考过程,提高解题速度.在结论1及结论2的证明过程中得到以下椭圆的焦半径公式的三角形式.

结论3 设椭圆方程左右焦点分别为F1,F2,点P为椭圆上一点,PF1与x轴所成的角为θ,PF2与x轴所成的角为α,c为椭圆的半焦距,则

例3 设椭圆的左右焦点分别为F1,F2,过F1作椭圆的长轴的垂线交椭圆于点P,若△F1PF2为等腰直角三角形,则椭圆的离心率为____.

点评例3根据公式可以直接计算三角形边长|PF1|,进而得到a,c关系式,求出离心率.一般方法可以先求出点P坐标,再有两点间的距离公式计算|PF2|.例4利用公式直接计算出假设满足条件的两个焦半径长度.再根据椭圆定义直接给出满足条件的解的个数.而一般方法通过勾股定理和椭圆的定义解得|PF1|=|PF2|=4.比较而言,我们的方法更为节时而精准.由结论3可得到过焦点弦的弦长公式.

证明如图(1),考虑AB所在直线倾斜角为直角或锐角且该直线经过F1的情形,对于其它情形可以相仿地讨论.由结论

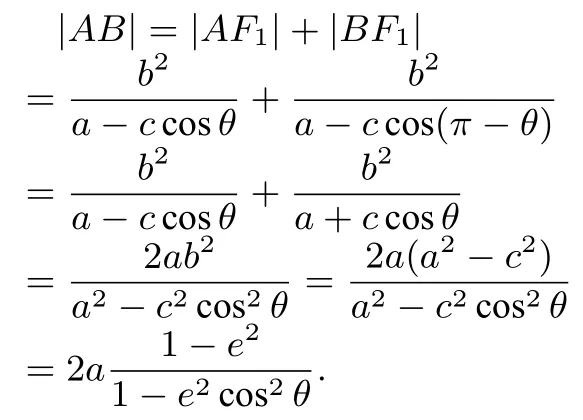
图1

(1)求椭圆的方程;

证明如图2,考虑AB过F1且θ为直角或锐角的情形,其它情形证明相仿.由结论 4得则焦点F2到直线AB的距离d=

图2

点评以上例5—7都可以用联立直线、椭圆方程组化为二次方程,利用根与系数、弦长公式计算弦长、点到直线的距离公式等知识点求解.但比较而言,这里给出的方法更为简洁.