一道高考题引发的思考*
●周杭敏
(萧山区第六高级中学 浙江杭州 311261)
一道高考题引发的思考*
●周杭敏
(萧山区第六高级中学 浙江杭州 311261)
在高中数学中,我们常见的是已知初始值,且函数f(x)或数列{an}满足三阶递推式子,求当x或者n取较大值时函数f(x)或数列{an}的值.解决这个问题的关键是求出此时函数或数列的周期.平时解题中一般都是通过列举法求出周期,这种方法运算量较大,而且不太适用周期较大的函数,因此一种较为简单且利于学生计算的方法迫在眉睫.文章讨论函数f(x)或数列{an}满足三阶递推式子时求其周期性的一种新方法,并给出了最小正周期.
三阶递推;周期性;最小正周期
函数在高中数学中有着举足轻重的地位,也是高考压轴题考查的重点,周期性是函数的一个重要性质.而数列又是一种特殊的函数,利用函数的思想方法类比函数的周期性解决周期数列的有关问题,实现函数思想方法的正迁移,有利于知识的构建与重整.函数f(x)或周期数列{an}因其优美的周期性常常受到高考和竞赛的青睐.
题目 定义在R上的函数f(x)满足
求f(2 016)的值.
(2016年浙江省杭州市高三名校第1次模拟考试题)
分析 本题考查对数的运算性质和函数周期性,以及归纳推理的能力.根据函数的表达式,利用题中递推式子推导得出“当x>0时函数的周期”,再根据f(x)的周期性,求解f(2 016)的值.
解 对任意的x>0,由
f(x+6)=f(x+5)-f(x+4)=
f(x+4)-f(x+3)-f(x+4)=
-f(x+3)=-[f(x+2)-f(x+1)]=
-[f(x+1)-f(x)-f(x+1)]=f(x),得
f(x+6)=f(x),
即当x>0时,f(x)的周期为6.因此,
f(2 016)=f(336×6)=f(6)=f(5)-f(4)=
[f(4)-f(3)-f(4)]=-f(3)=
-[f(2)-f(1)]=
-[f(1)-f(0)-f(1)]=
f(0)=log21=0.
从上述解答中可以发现:解决这道题的关键是求出当x>0时函数的周期.由于该解法需要由递推式子逐步地推导出函数的周期,运算量较大,而且此解法不太适用于当函数满足某种递推式子时周期比较大的情况.因此,笔者在上述解法之外探寻新的方法如下:
由f(x)=f(x-1)-f(x-2),得特征方程[1]
x2=x-1,
即
x2-x+1=0,
解得

图1

f(x)=f(x+6).
从上述方法中可以看出,由f(x)=f(x-1)-f(x-2)可以推出f(x)的周期.在高中数学中,最常见的是已知函数或数列满足三阶的递推式子,通过函数f(x)或数列{an}的周期性来求一些特殊的函数值或数列值,因此研究函数满足递推式子时的周期性很有必要.而解决此类问题的关键是函数f(x)或数列{an}满足三阶递推式子时,求函数f(x)或数列{an}的周期性.是否所有函数f(x)的三阶递推式子都可以求出周期呢?如果不是,那么函数f(x)满足何种三阶递推式子时,函数f(x)具有周期性?此时f(x)的周期是多少?是否具有最小正周期?
定理 若函数f(x)满足三阶递推式子
f(x+2)=mf(x+1)+nf(x),

证明 不妨设一般的三阶递推式子为
f(x+2)=mf(x+1)+nf(x),
其中m,n∈R.由特征方程理论可知:f(x+2)=mf(x+1)+nf(x)的特征方程为
x2-mx-n=0.
1)当Δ=m2+4n≥0时,特征方程有2个实根,此时f(x)不具有周期性.
2)当Δ=m2+4n<0时,特征方程有2个复数根.设特征方程的复数根为x1,x2,且

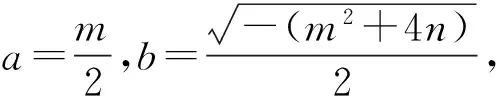
又根据欧拉公式[1],得
x1=r(cosθ+isinθ)=reθi,
nθ=mθ+2kπ,其中k∈Z,
从而

因此,对任意的n,m,且n≠m,

即z1的正周期是
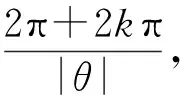
从而可知x1的正周期是
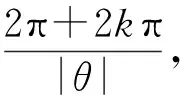
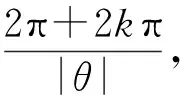
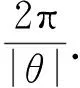

[1] 钟玉泉.复变函数论[M].3版.北京:高等教育出版社,2008.
[2] 朱长江.偏微分方程[M].武汉:华中师范大学出版社,2005.
2016-11-02;
2016-12-06
周杭敏(1992-),女,浙江杭州人,中学二级教师.研究方向:数学教育.
O12
A
1003-6407(2017)04-42-02

