Application of EMD filtering based on l2-norm in denoising FOG signal
LI Yu-huan, YANG Gong-liu, LIU Yuan-yuan
(1. School of Instrumentation Science & Opto-electronics Engineering, Beihang University, Beijing 100191, China;
2. Science and Technology on Inertial Laboratory, Beijing 100191, China;
3. Beijing Aerospace Times Optical-Electronic Technology Co., Ltd, Beijing 100854, China)
Application of EMD filtering based on l2-norm in denoising FOG signal
LI Yu-huan1,2, YANG Gong-liu1,2, LIU Yuan-yuan3
(1. School of Instrumentation Science & Opto-electronics Engineering, Beihang University, Beijing 100191, China;
2. Science and Technology on Inertial Laboratory, Beijing 100191, China;
3. Beijing Aerospace Times Optical-Electronic Technology Co., Ltd, Beijing 100854, China)
To reduce the random noise and drift of fiber optic gyros (FOG), a novel Hurst-exponent-based signal filtering method is introduced, which combines the empirical mode decomposition (EMD) and the similarity measure between the probability density function (pdf) of the signal and the pdf of each mode. When H<0.5, the relevant modes are selected by using l2-norm, and the partial reconstruction with relevant modes is formed and used to filter the FOG’s noisy signals; When H≥0.5, EMD interval thresholding (EMD-IT) is introduced into the relevant modes to carry on filter processing, then the FOG’s noisy signals are filtered according to partial reconstruction approach. This method is called as mixed EMD-pdf & EMD-IT method. Simulation and real data test are carried out to evaluate the effectiveness of the proposed method. Other EMD denoising methods, such as correlation-based EMD reconstruction (EMD-cor), single pdf-based EMD reconstruction (EMD-pdf), are also investigated to provide a comparison with this method. Experiment results show that its performance is superior to those of the other EMD denoising methods.
fiber optic gyroscope; empirical mode decomposition; l2-norm; random drift
Fiber optic gyroscope (FOG), as a kind of inertial sensors, has been widely used in inertial navigation system (INS) because of its significant advantages[1-3]. However, the random drift is the most remarkable issue that contributes to the performance degradation in inertial sensors[4-5]. Among different ways to restrain the random drift, mathematical models and denoising methods are two main techniques realized by software technology reported in relevant literatures.
Empirical mode decomposition (EMD), first introduced by Huang et al. in [6], has been used for analyzing the non-linear and non-stationary signal processes by adaptively decomposing any signal into oscillatory components called intrinsic mode functions (IMFs)[7-8], where wavelet filtering has been the dominant technique for many years[9]. As opposed to wavelet filtering, EMDadaptively expresses the signal as an expansion of basic functions directly derived from the signal itself[10]. Recently, many EMD-based denoisings have been provided to remove noises from observed data, which can be classified into two main categories, i.e. the whole reconstruction with filtered modes and the partial reconstruction with relevant modes.
Boudraaet al. in [9] proposed a variety of different whole reconstruction signal denoising schemes. However, it is limited to signals with white Gaussian random noise. Later, Boudraaet al. proved that EMD-based partial reconstruction performs in an adaptive way in [11], but in some cases, CMSE criterion can be trapped in local minima. A correlation-based threshold is established to distinguish relevant modes in reference [12], and its disadvantage is sensitive to different signal-to-noise power ratios (SNR). Kopsinis and Mclanglin developed a series of novel EMD-based denoisings inspired by wavelet thresholding in [13], where EMD interval thresholding termed EMD-IT is provided, while the relevant modes were selected based on experience. Quet al. provided a novel EMD-based mode cell filtering (MCF) method in [14] and selected the relevant modes from experience. Komatyet al. in [15] put forward a similarity measure between the probability density function (pdf) of the input and that of each extracted mode to determine the relevant modes, and the best results are given by the geometric similarity measures, especiallyl2-norm measure. However, the position of the first local maximum is proved to move forward by simulation when Hurst exponent of fractional Gaussian noise (fGn) increases. According to the statistical characterristics of white Gaussian noise and the fGn through EMD, the energy of noise decays at a slower rate whenHis close to 1. Thus it is disastrous for the EMD partial reconstruction usingl2-norm measure to select relevant modes. To avoid these shortcomings, a novel EMD-based signal filtering is introduced in this paper which combines Hurst exponent andl2-norm measure. WhenH≥0.5, EMD-IT is added to further denoise each relevant modes called mixed EMD-pdf & EMD-IT method; then the same partial reconstruction is implemented asH<0.5. Numerical simulation and real data test were carried out to evaluate the effectiveness of this proposed method.
1 Brief review of EMD
A noisy signalx(t) is adaptively broken down intoLIMFs by EMD, termedh(i)(t) (1≤i≤L). Those basic building blocks are obtained through a sifting process according to the following steps[9]. A schematic of the inner and outer loops of the EMD is shown in Fig.1.
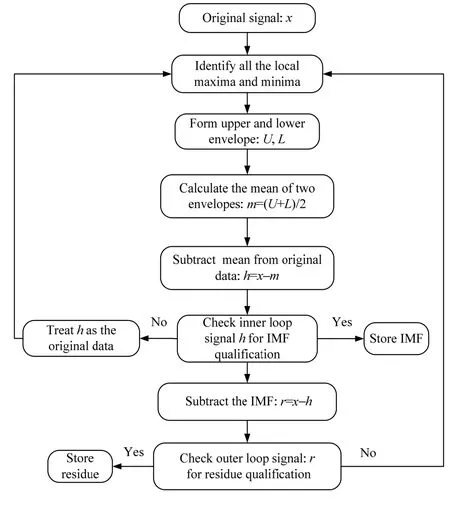
Fig.1 Pictorial representation of empirical mode decomposition
The extracted modes are nearly orthogonal to each other, which form a complete set because accumulating all modes with the residual can restore the decomposed signal. The signal can be expressed as follows:

2 Principle of EMD-based denoising
Consider a noiseless signaly(t) contaminated by an additive noisen(t):

The denoising is to find an estimate(t) of the observed signalx(t). For EMD-based partial reconstructtion denoising,(t) is given by
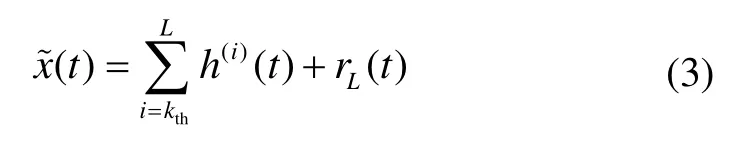
To identify the relevant modes of decomposed signal, the signal is first decomposed into several IMFs followed by an estimation of their pdfs using the kernel density estimator. The two pdfs, namedPandQ, can be seen as two sets of points. Thel2-norm is defined by
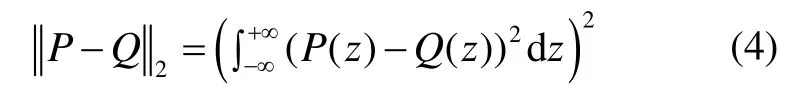
From Eq.(4), we can see that thel2-norm is sensitive to the variation of the distance between two correspondding points. The similarity measure usingl2-norm is defined as follows:
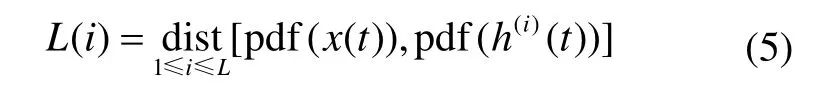
The “dist” stands for the distance between two pdfs measured by l2-norm. The first selected mode is the one when the distance starts decreasing after the first local maximum. The kthis identified by
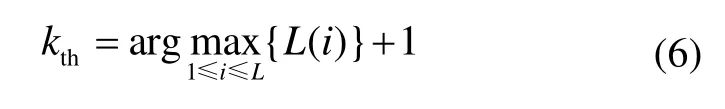
Fig.2 illustrates how this novel filtering works, where EMD-IT is applied to each relevant mode to further eliminate the effect of noises. Details on the EMD-IT are fully available in [13]. EMD-IT can effectively reduce the discontinuity. With respect to the threshold selection, the universal threshold is a popular candidate.
3 Results and discussions
To verify the effectiveness of this novel denoising method, the noisy signals considered in this section include simulation and real test signals.
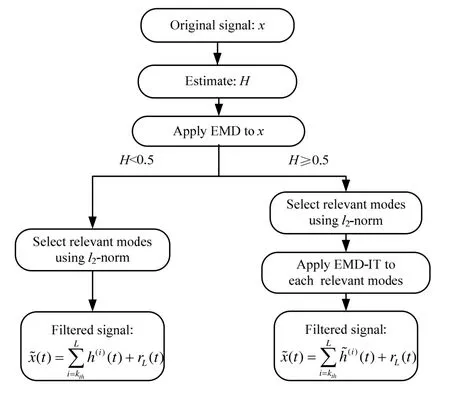
Fig.2 Illustration of novel filtering scheme using l2-norm
3.1 E xperiment 1
To illustrate the effectiveness of this proposed filtering, the EMD-cor and EMD-pdf methods are also investigated as comparisons in this paper. The code of EMD can serve as reference implementation.
For the noisy “Doppler” signal with length 2048, three denoising methods can restore the denoised signal, as shown in the Fig.3. In Fig.3(1), EMD-pdf exhibits the same behavior with EMD-cor for the SNR=12.04 dB. In contrast, the mixed EMD-pdf & EMD-IT enhances the performance of denoising where the SNR is up to 13.34 dB. In Fig.3(2), the gains in SNRs are respectively up to 8.15 dB and 8.03 dB by EMD-cor and EMD-pdf, while the mixed method improves the SNR up to 9.65 dB.
From the Fig.3, we can see that the mixed EMD-pdf & EMD-IT method has better results compared with other two methods. In this paper, we proposed this mixed method only used when H≥0.5.
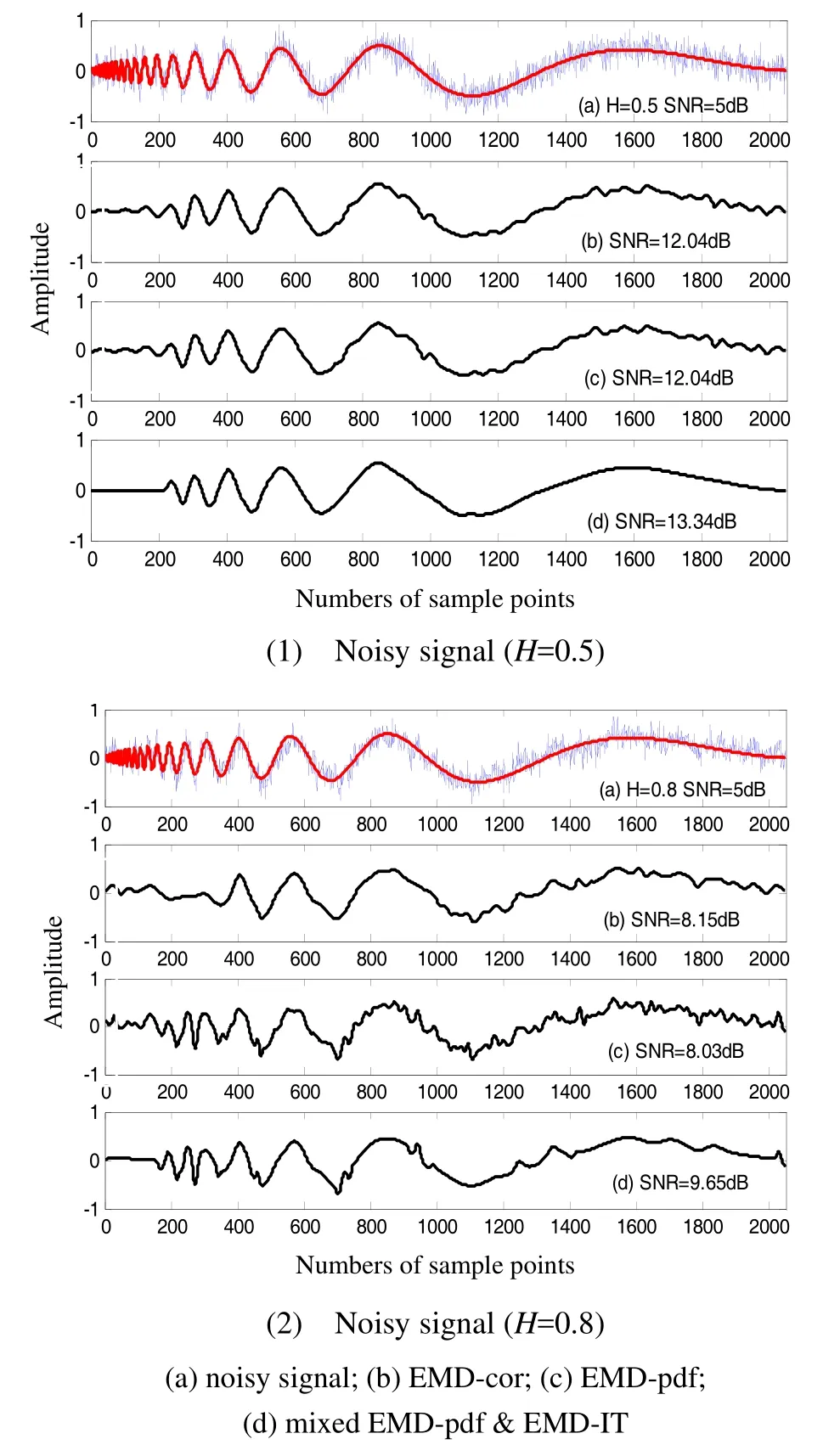
Fig.3 Results of filtered signals
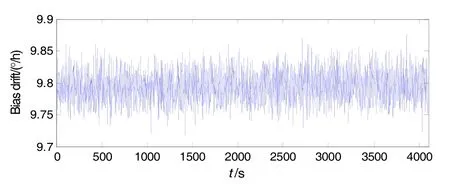
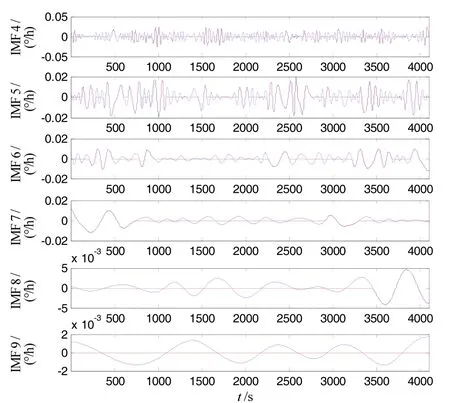
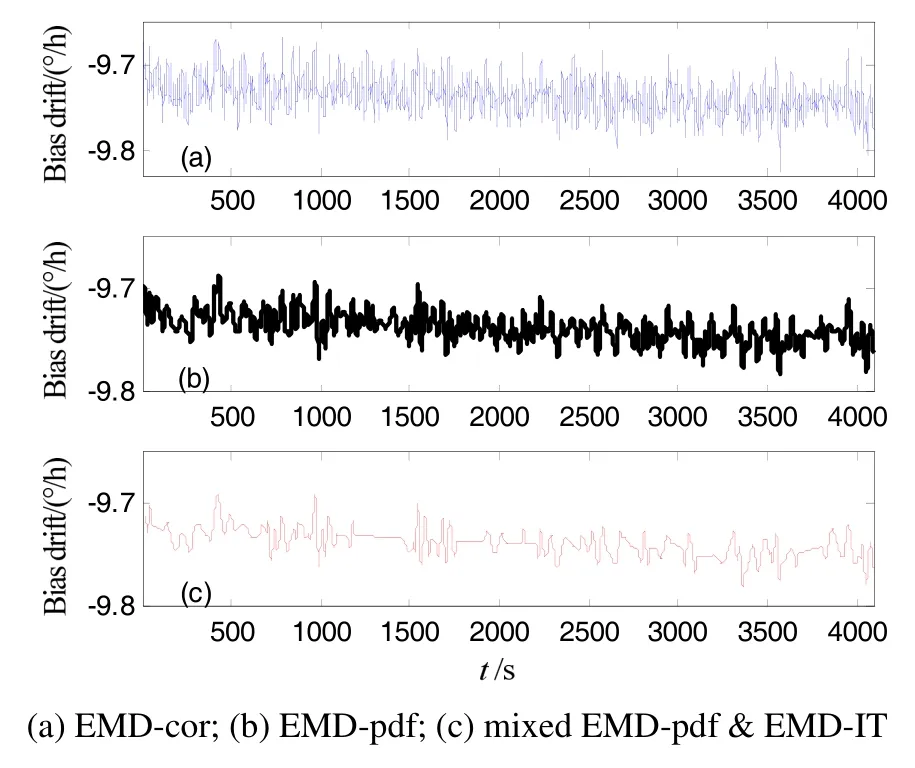
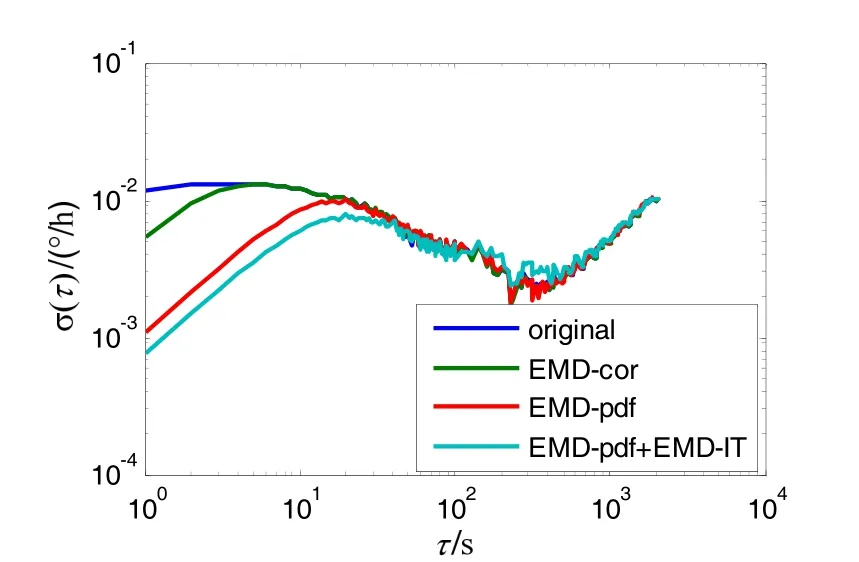
We have performed numerical simulations for the signals of “Blocks”, “Bumps”, “Heavysine”, and “ECG”, which were generated using Matlab software and the size is N=2048. We have adopted short (0 Fig.4 Results of EMD-based filtering 3.2 E xperiment 2 Under the normal temperature (25℃), we make experiment testing for FOG drift signal. The sample period is 1 s, and the total number of samples is N=332 852. To avoid the variation of temperature in startup time, this paper selects the samples length of 4096 from 14 097~ 18 193 to assess the filtering, shown in Fig.5, such as EMD-cor, EMD-pdf, mixed EMD-pdf & EMD-IT. The H of the signal is 0.7880 estimated by the wfbmesti function in Matlab, which affirms the fact that the timecorrelation colored noise really exists in inertial sensors. Fig.5 FOG drift signal Based on the EMD-cor, the kthis 2 where the correlation coefficient between the input and its modes starts smaller than the prefixed threshold. In contrast, the kthis 4 using l2-norm, less relevant modes are selected as useful signal for partial reconstruction. Additionally, our proposed mixed EMD-pdf & EMD-IT method is applied on the selected relevant modes to further filter the noises. To illustrate the differrence between EMD-pdf and the mixed EMD-pdf & EMD-IT, the results of relevant modes with IMFs number 4 to 9 before and after denoising are shown in Fig.6, where red lines are the filtered signal, those relative smaller mode cells are considered noises and discarded. Fig.6 Relevant modes before and after EMD-IT denoising The denoising results using EMD-cor, EMD-pdf, mixed EMD-pdf & EMD-IT method are given in Fig.7.To verify the denoising performance, the most commonly used Allan variance for FOG noise analysis is employed as the criterion. As shown in Fig.8, the proposed method can effectively filter the noise, where the mixed method has lower slope as compared to EMD-cor and EMD-pdf. Fig.7 Results of EMD-based filtering Fig.8 Allan variance analysis before and after denoising In this paper, a novel mixed EMD-pdf & EMD-IT method is proposed to filter noisy signals when H≥0.5 and a single EMD-pdf method is used when H<0.5, where the l2-norm is used to select relevant modes. However, the first local maximum obtained from l2-norm is sensitive to the form of noise. Thus, according to the value of H, the mixed or the single method is chosen for denoising. In addition, the threshold is estimated on the basis of the characteristics of fGn through EMD. To illustrate the effectiveness of this proposed method, we carried out numerical simulations with different SNR under each H level. This improved method exhibits an enhanced performance of denoising compared with EMD-cor and EMD-IT methods. Finally, this proposed method is applied to the real signal: FOG drift signal. From the Allan variance curves, we can see that the random error has been greatly decreased by the mixed EMD-pdf and EMD-IT method. Hence, the proposed FOG denoising algorithm has been proved to have potential applications in INS domain. [1] Liu Y Y, Yang G L, Li S Y. Application of BP-Bagging model in temperature compensation for fiber optic gyroscope[J]. Journal of Chinese Inertial Technology, 2014, 22(2): 254-259. [2] Liu Y Y, Yang G L, Li S Y. Application of BP-AdaBoost model in temperature compensation for fiber optic gyroscope bias[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(2): 235-239. [3] Liu Y Y, Yang G L, Li S Y. Temperature compensation for fiber optic gyroscope based on dual model[J]. Journal of Chinese Inertial Technology, 2015, 23(1): 131-136. [4] Liu Y Y, Yang G L, Li M, et al. Variational mode decomposition denoising combined the detrended fluctuation analysis[J], Signal Processing, 2016, 125: 349-364. [5] Yang G L, Liu Y Y, Li M, et al. AMA- and RWE-based adaptive Kalman filter for denoising fiber optic gyroscope drift signal[J]. Sensors, 2015, 15: 26940-26960. [6] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[C]//Proceedings of the Royal Society of London, Series A, 1998, 454(3): 903-995. [7] Zhang S Y, Liu Y Y, Yang G L. EMD interval thresholding denoising based on correlation coefficient to select relevant modes[C]//Proceedings of the 34th Chinese Control Conference. 2015: 4081-4086. [8] Huang M, Liu Y Y, Yang G L, et al. An innovation based DFA and EMD method for denoising fiber optic gyroscope drift signal[C]//Proceedings of the 3rd International Conference on Information Science and Control Engineering. 2016: 1262-1266. [9] Yang G L, Liu Y Y, Wang Y Y, et al. EMD interval thresholding denoising based on similarity measure to select relevant modes[J]. Signal Processing, 2015, 109: 95-109. [10] Tsakalozos N, Drakakis K, Rickard S. A formal study of the nonlinearity and consistency of the empirical mode decomposition[J]. Signal Proceesing, 2012, 92(9): 1961-1969. [11] Boudraa A O, Cexus J C. EMD-based signal fi ltering[J]. IEEE Transactions on Instrumentation and Measurement, 2007, 56(6): 2196-2202. [12] Ayenu-Prah A, Attoh-Okine N. A criterion for selecting relevant intrinsic mode functions in empirical mode decomposition[J]. Advance in Adaptive Data Analysis, 2010, 2(1): 1-24. [13] Kopsinis Y, Mclanglin S. Development of EMD-based denoising methods inspired by wavelet thresholding[J]. IEEE Transactions on Signal Processing, 2009, 57(4): 1351-1362. [14] Qu C S, Yu H, Xu H L, et al. Random signal de-noising based on empirical mode decomposition for laser gyro[J]. Infrared and Laser Engineering, 2009, 38(5): 859-863. [15] Komaty A, Boudraa A O, Augier B, D. et al. EMD-based filtering using similarity measure between probability density functions of IMFs[J]. IEEE Transactions on Instrumentation and Measurement, 2014, 63 (1): 27-34. 1005-6734(2017)02-0244-05 基于l2范数的EMD滤波方法在光纤陀螺信号中的应用 李宇寰1,2,杨功流1,2,刘元元3 (1. 北京航空航天大学 仪器科学与光电工程学院,北京 100191;2. 惯性技术国防重点实验室,北京 100191;3. 北京航天时代光电科技有限公司,北京 100854) 光纤陀螺的随机漂移限制了惯性导航系统的精度,如何减小它是一项非常艰巨的任务。结合经验模态分解(EMD)和信号与模态之间的概率密度函数,提出了一种新型的依赖Hurst指数的信号滤波方法。当H<0.5时,利用l2范数选择出相关模态,累加并形成的部分重构方法来对光纤陀螺的信号进行滤波;当H≥0.5时,间隔阈值的经验模态(EMD-IT)被引入对相关模态进行滤波,之后按照部分重构的方法对光纤陀螺的信号进行滤波;称为混合的EMD-pdf和EMD-IT。与其它的滤波方法进行对比,如基于相关函数的EMD部分重构(EMD-cor),基于概率密度函数的EMD部分重构(EMD-pdf),仿真信号和实际数据结果表明,该混合模型的优越性,有效减小了光纤陀螺的随机误差。 光纤陀螺;经验模态分解;l2范数;随机漂移 V241.5 A 2017-01-04; 2017-03-24 国家自然科学基金(61340044,11202010);中央高校基本科研业务费专项资金资助项目(YWF-10-01-B30) 李宇寰(1978—),男,博士研究生、陆军参谋,从事惯性技术研究。E-mail: lyhzl1112@163.com 联 系 人:杨功流(1967—),男,教授,博士生导师。E-mail: bhu17-yang@139.com 10.13695/j.cnki.12-1222/o3.2017.02.020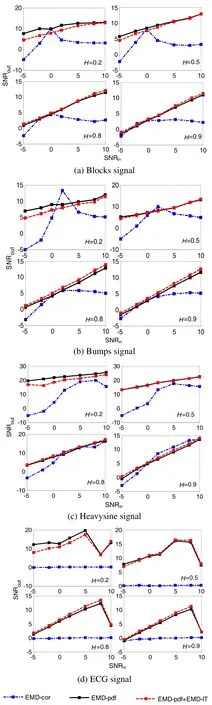
4 C onclusion

