基于萤火虫群优化的空间非合作目标相对导航粒子滤波算法

张大力，夏红伟，马广程，王常虹

（哈尔滨工业大学 航天学院，哈尔滨 150001）

基于萤火虫群优化的空间非合作目标相对导航粒子滤波算法

张大力，夏红伟，马广程，王常虹

（哈尔滨工业大学 航天学院，哈尔滨 150001）

研究了空间非合作目标相对导航算法，针对标准粒子滤波的重采样过程导致的粒子贫化现象及其造成的相对导航精度下降问题，分析了萤火虫优化算法的运行机制，提出一种基于萤火虫智能优化算法的改进粒子滤波算法。改进算法通过优化粒子滤波的重采样过程，使粒子群智能的向高似然区域移动，同时在低似然区域也合理保留了部分粒子，保证了粒子的多样性，提高了样本的整体质量。仿真结果表明，改进算法导航精度较标准算法提高了39.35%，达到稳定精度所需粒子数较少，有效抑制了粒子贫化问题。

萤火虫算法；粒子滤波；粒子贫化；相对导航

航天器的相对导航是实现在轨服务和编队飞行任务的基础，直接影响控制和制导精度[1]。目前对空间合作目标的相对导航研究基本趋于成熟，对非合作目标如故障、失效卫星或空间碎片等的研究较少，是目前航天领域研究的热点[2]。经典方法基于线性系统和高斯噪声假设，利用目标的反馈信息，通过扩展卡尔曼滤波(EKF)估计目标的真实相对状态[3]。

非合作目标的运动往往无法用线性模型描述，且实际噪声通常不满足高斯分布，需要转化为线性问题处理，导致 EKF估计效果急剧下降。无迹卡尔曼滤波较 EKF具有更好的非线性滤波性能，但对于非高斯噪声问题依然缺乏适应性[4]。粒子滤波是近年来逐渐发展成熟的基于蒙特卡洛思想的滤波技术，不受系统非线性和非高斯条件的限制[5]，得到国内外学者的青睐，取得了很多研究成果。然而标准粒子滤波采用重采样技术，复制大权值样本，小权值粒子被直接舍弃，这导致了粒子的贫化问题。客观来讲，虽然小权值粒子对滤波估计贡献有限，但其中仍包含了一定的状态信息，直接舍弃势必影响滤波精度，这限制了粒子滤波的发展和应用前景。

针对这种粒子贫化问题，国内外学者进行了大量研究。Zhao[6]利用MCMC方法通过构造Markov链产生随机样本，增加了粒子多样性，但增加了计算量；Sun[7]引入辅助变量近似后验密度，减少了权值方差，但对噪声适应性较差；Li[8]利用遗传算法的进化思想对粒子滤波进行改进，一定程度上提高了滤波实时性；Liu[9]利用粒子群算法的全局寻优能力优化粒子滤波，减少了滤波所需粒子数，但容易陷入局部最优。

LI[10]利用人工鱼群算法对粒子滤波进行优化，收敛速度快，但精度不高。受此启发，本文引入萤火虫群智能优化思想，在对其运行机制进行改进的基础上优化粒子滤波的重采样过程，改善粒子贫化问题，提高导航精度，并通过仿真结果验证算法的有效性。

1 相对导航问题状态模型与观测模型

1.1 相对运动状态模型

考虑空间两在轨目标的近距离相对运动，推导相对运动动力学方程，为跟踪滤波算法提供状态方程。在可观测条件下，两星在轨运行情况如图1所示，其中：C为追踪星(Chaser)，运行于近圆轨道；T为目标星(Target)，为非合作目标。令追踪星轨道坐标系为o-xyz，原点o位于追踪星质心，ox轴沿地心矢径方向指向卫星，oy轴指向追踪星飞行的切线方向，oz轴垂直于轨道平面向上，三轴满足右手定则。

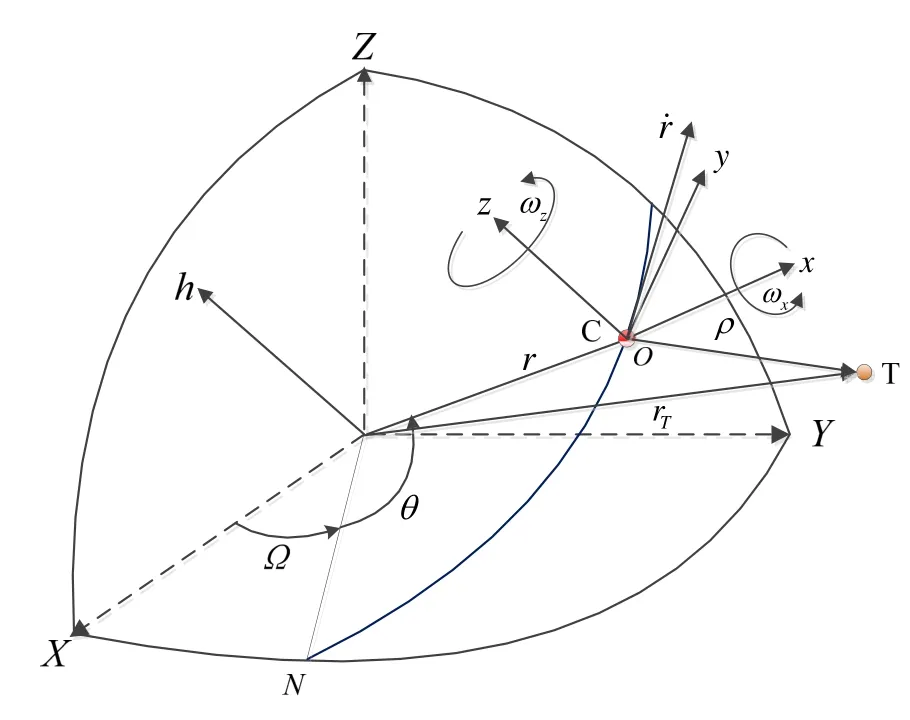
图1 相对运动示意图Fig.1 Relative motion diagram

由牛顿第二定律得追踪星和目标星对惯性空间的运动方程为

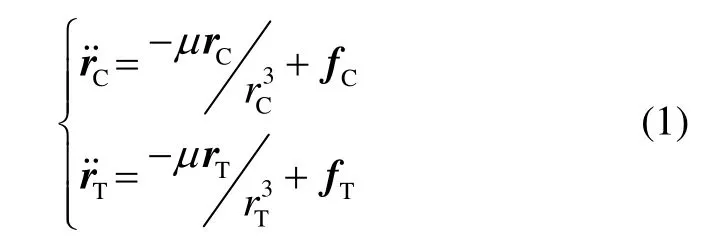
式中：rC、rT为地心到C和T的矢量；μ为地心引力常数；fC、fT为控制力和空间摄动力作用下C和T的加速度矢量。

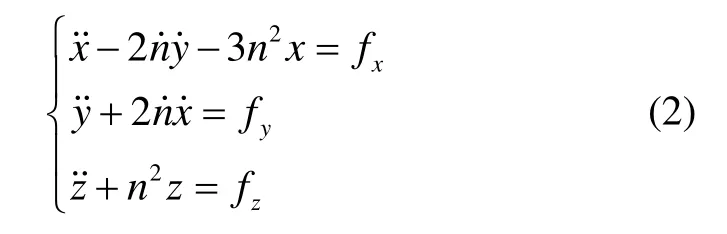
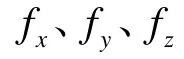
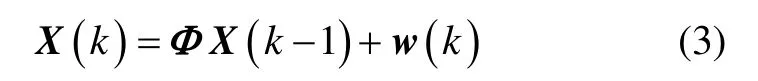
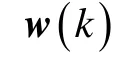
1.2 观测模型确定

本文采用“光学测角相机+激光测距仪”的观测模式，如图2所示。

光学测角相机可以给出T在o-xyz系下方位角(A)和高度角(E)，激光测距仪可提供C与T的相对距离ρ。

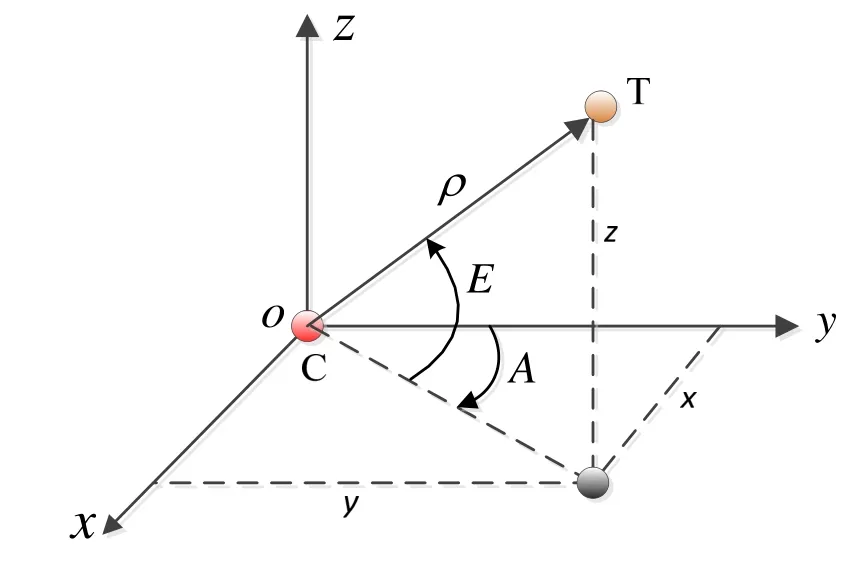
图2 观测模型示意图Fig.2 Observation model diagram

以上参数与相对轨道坐标的关系可以表示为

式中：

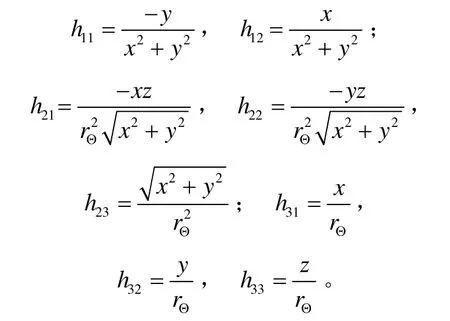
观测方程可写成如下形式：

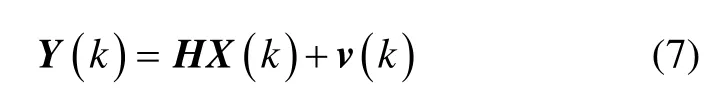
式中：Y(k)为k时刻的观测量；v(k)为闪烁噪声。

概率密度分布为

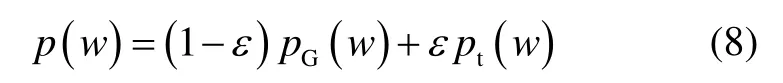
公式(3)和(7)组成了相对导航问题的状态方程和观测方程。需要补充的是，本文不考虑导航过程中姿态变化等因素导致的设备测量坐标系与轨道坐标系不重合现象，避免了繁琐的坐标转换。

2 粒子滤波分析

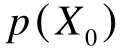
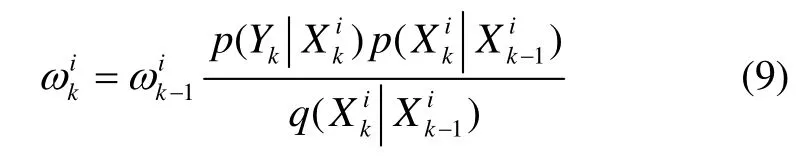
通常情况下，先验密度函数被选为重要密度函数，即：

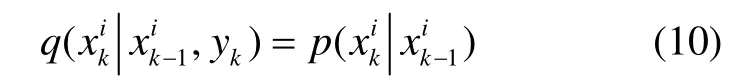
当用重要性函数替代后验概率分布作为采样函数时，理想情况是重要性函数非常接近后验概率分布。而在实际问题中，通常使用式(10)中的次优重要性概率密度代替。当观测值较准确或似然函数位于先验概率密度尾部时，似然概率与先验概率分布的重叠部分就会很小，权重更新后许多粒子的权重会变得很小，经重采样过程，多数粒子就会被筛选掉，严重时甚至仅剩单一粒子，从而导致粒子贫乏问题，影响滤波精度。

3 萤火虫群优化粒子滤波算法

3.1 萤火虫算法

萤火虫算法是模拟萤火虫群的群体行为的随机优化算法，由剑桥学者yang[11]于2009年提出，是最新的智能优化算法之一，具有良好的收敛速度和精度，实现简单，易于工程实现。其仿生原理为：搜索空间中的点抽象为萤火虫个体，寻优过程模拟个体间的吸引和移动过程，优化目标抽象为个体位置的优劣。算法遵循下列理想行为规则：

1）所有萤火虫无性别，每个萤火虫均可吸引其他萤火虫而与它们的性别无关。

2）吸引度与它们的亮度成正比，并随着距离的增加而减少，若两个个体亮度完全相同，则自由移动。

3）荧光亮度由要优化的目标函数值决定。

算法包含两个要素：亮度和吸引度。亮度体现了个体所处位置的优劣并决定其移动方向，个体受到的吸引度决定了其移动的距离。通过对这两个核心要素的更新实现迭代寻优过程。其参数化表述如下：

1）萤火虫的相对荧光亮度为

其中：I0代表光源的光强；γ近似代表固定的光吸收系数，典型取值范围(0.1, 10)；rij代表萤火虫个体间的空间距离。

2）萤火虫吸引度公式为

其中，β0为最大吸引度，通常取值为1。

3）在t时刻，萤火虫个体i被个体j吸引并向后者移动的位置更新公式为

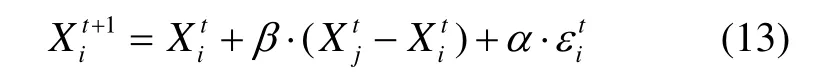
3.2 优化算法改进

针对粒子滤波的存在的问题，本文拟采用萤火虫算法的寻优能力优化粒子滤波的重采样过程。由萤火虫算法的原理可知，萤火虫算法与粒子滤波算法有一定相似之处，前者通过更新个体荧光亮度和位置来寻求最优值，后者通过更新粒子权值和位置来逼近系统真实后验概率密度。

由于萤火虫算法本身运行机制的特殊性，直接进行算法融合会带来一系列问题，如循环嵌套和粒子交互导致算法复杂度大幅增加等，因此本文对萤火虫算法中的荧光亮度进行重定义，对吸引度更新机制进行改进。

1）荧光亮度重定义

在粒子滤波中，权值ω是评价粒子的重要参量，越接近真实值权重越大；在萤火虫算法中，个体越接近最优值亮度越高。将荧光亮度定义为粒子权值，即

重新定义的荧光亮度公式意义更为明确，同时避免了不必要的运算，降低了运算复杂度。

2）改进吸引度更新公式

利用萤火虫算法吸引度和位置更新公式模拟不同权重粒子的移动过程，低权值粒子受高权值粒子吸引，向后者移动，自身权重提高。权重较小的粒子所携带的观测信息在估计结果中得到体现，避免了标准粒子滤波重采样过程简单复制替换带来的粒子退化现象。

3.3 算法具体实现和步骤

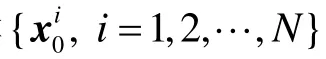
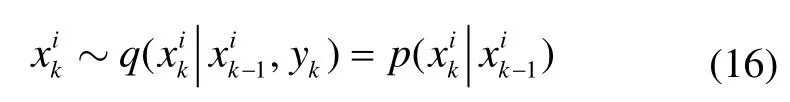
2）数据处理。粒子经状态模型和观测模型处理后分别得到k时刻的状态值和预测值。

3）权值更新。根据次优概率密度函数，结合预测值和实际观测值对权重进行更新。具体为

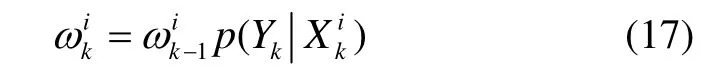
4）根据萤火虫算法，通过式(14)和式(15)得到萤火虫个体的亮度和相对吸引度。亮度的对比结果决定萤火虫移动方向，吸引度值代入式(13)得到个体移动距离。位置更新后进行亮度更新，并继续向更高亮度个体位置移动，形成迭代过程。引入最大迭代次数MaxG和终止阈值D，当亮度值大于D或达到最大迭代次数时停止优化。D的引入减少了在权值相近的情况下依然迭代至最大迭代次数的概率，提高了算法灵活性和效率。

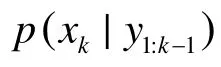
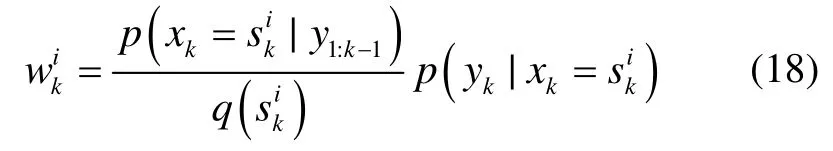
经补偿，粒子集在理论上服从同一分布，从而保证了算法的合理性。

6）归一化

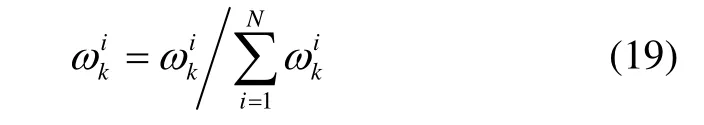
7）状态输出

4 仿真实验与分析

为进一步验证FA-PF算法对解决空间非合作目标相对导航问题的有效性，本文进行了仿真试验。仿真条件如表1所示。

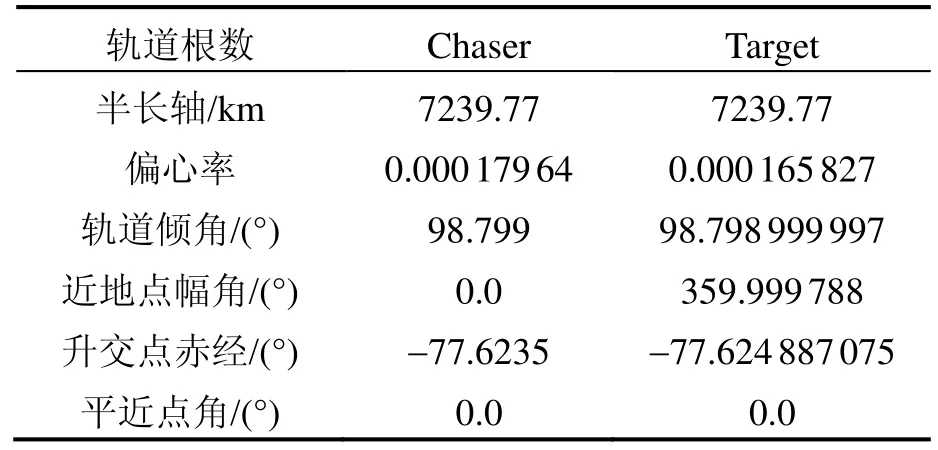
表1 航天器轨道根数Tab.1 Orbit elements of spacecraft

给定初值[0.173 176, 0, 0.100 001, 0, -0.000 205, 0]；根据某实际系统，标称测距精度 15 m (3σ)，测角精度0.3° (3σ)。采样周期为1 s，对10 800个时刻的相对状态信息进行滤波估计。

将初值分别代入PF和FA-PF算法，仿真时间设置为 10 800 s。设置间隔为25，给出粒子数在 25到200时的滤波结果，并分别对相对位置误差、相对速度误差和仿真时间进行对比。目标航天器在O-XYZ坐标系下的位置和速度为所需的相对轨道数据。

首先给出在不同粒子数下PF和FA-PF算法相对位置、相对速度和滤波时间的对比条形图，如图3～5所示。

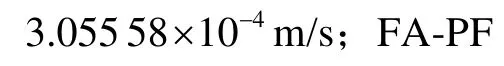
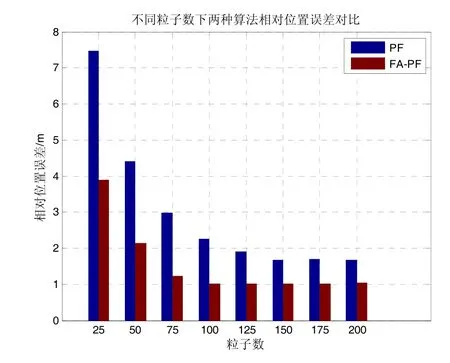
图3 相对位置误差对比Fig.3 Comparison on relative position errors

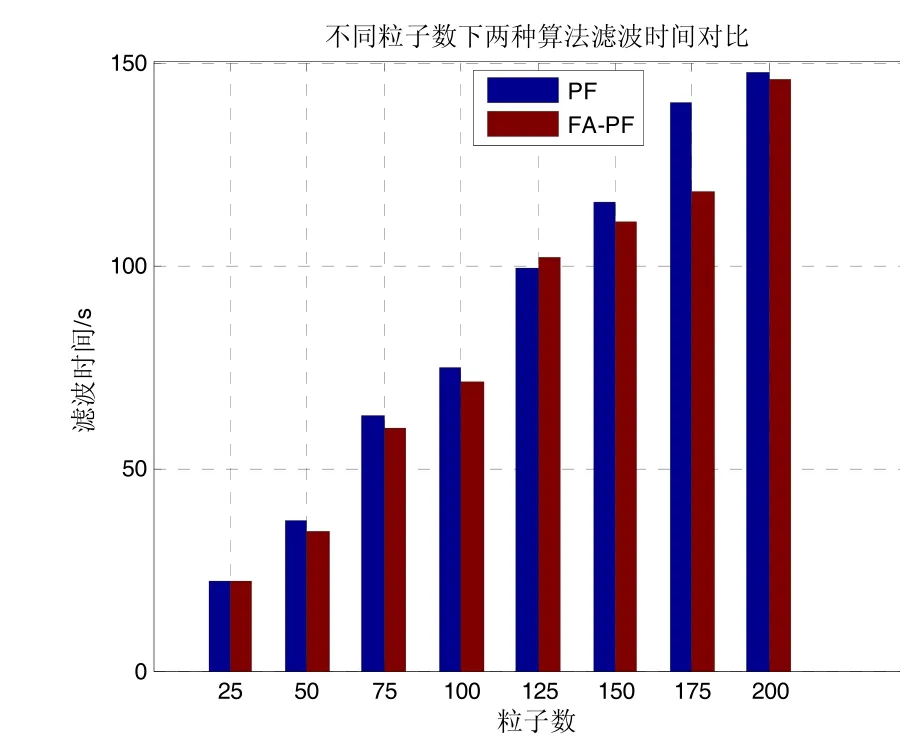
图5 滤波时间对比Fig.5 Comparison on filtering times

由图5可知，随着粒子数的增加，仿真时间在不断延长。相同粒子数下，PF和FA-PF算法仿真时间基本一致，前者略高于后者。当 PF算法在取150个粒子，仿真时间达到 115.564 15 s的情况下，才能达到最高精度，而 FA-PF算法在取 100个粒子，仿真71.152 52 s即可达到最高精度。

综合考虑，FA-PF在精度和时间上均优于PF算法。更直观的，给出取100粒子时PF和FA-PF算法的相对位置和速度误差曲线，如图6、图7所示。

由于设置仿真步数较多，为避免图像丢帧导致结果不直观，取曲线中 56个点来绘制相对位置和相对速度误差曲线。图 6和图 7显示，在相同条件下，FA-PF算法表现较PF算法稳定。为了更清晰地展示FA-PF算法对粒子贫化现象的抑制作用，给出状态输出前的粒子分布图，如图8所示。

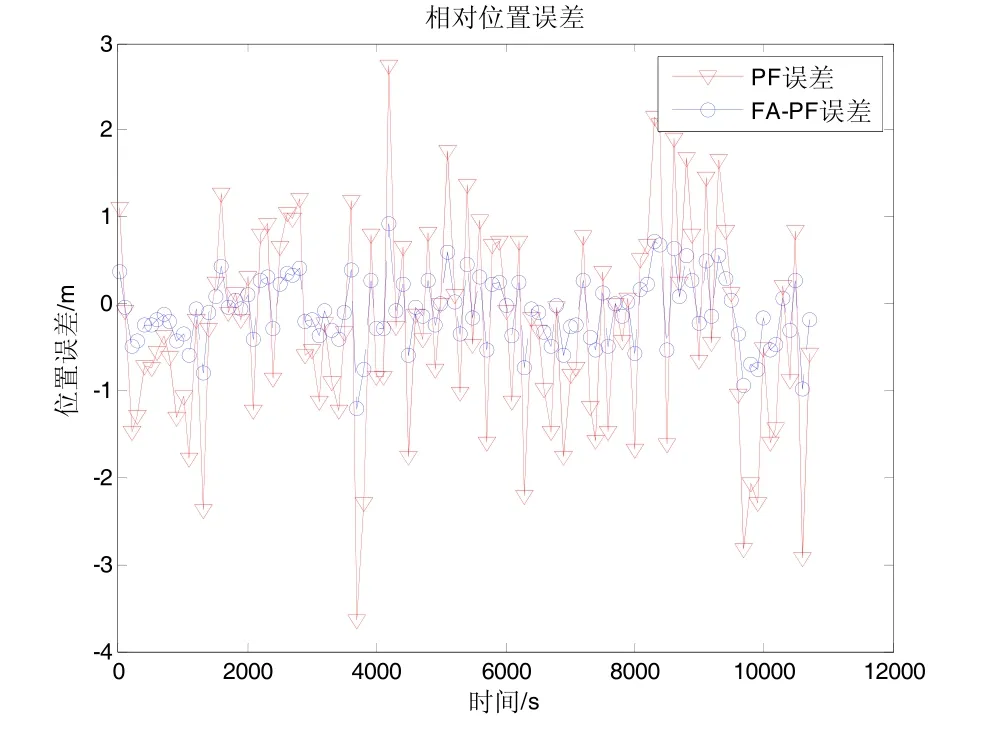
图6 100粒子相对位置误差对比Fig.6 Comparison on relative position errors of 100 particles

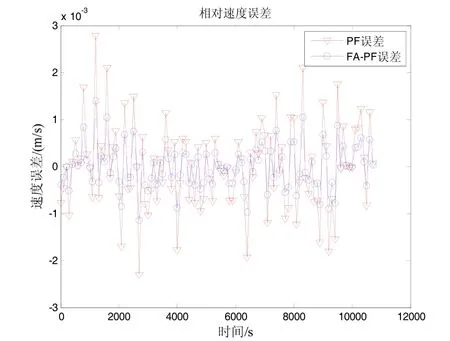
图7 100粒子相对速度误差对比Fig.7 Comparison on relative velocity errors of 100 particles

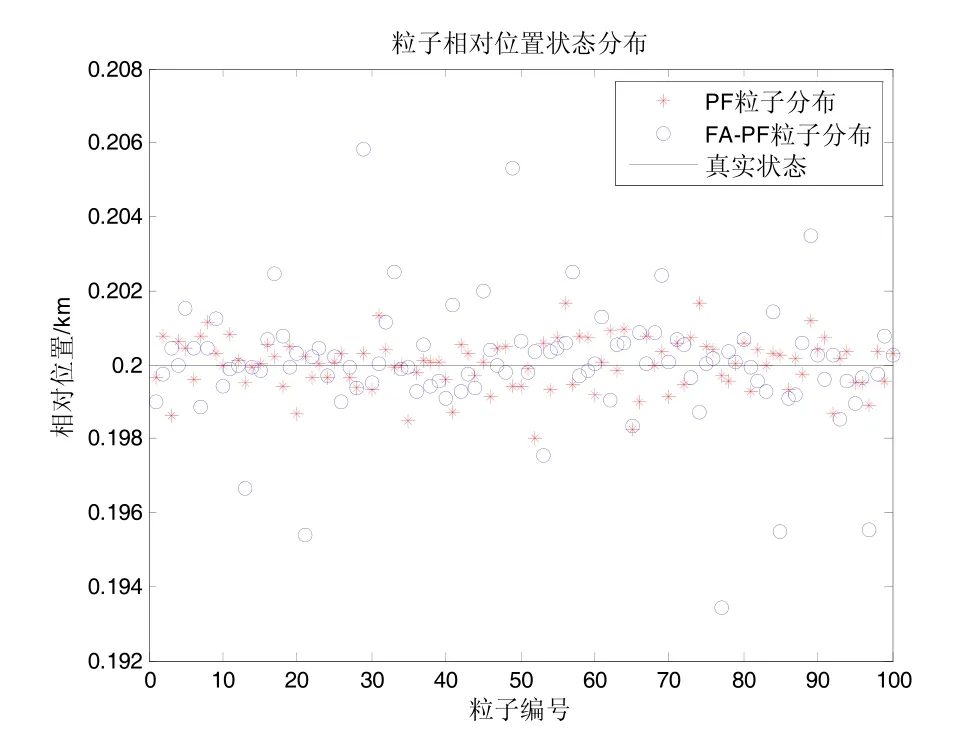
图8 粒子相对位置状态分布Fig.8 Relative position state distribution of particles

图6～8中，实线表示真实状态，“*”表示PF算法粒子分布，“。”表示FA-PF算法粒子分布。可以看出，标准粒子滤波算法粒子多样性表现一般，在有些位置分布较为集中，不利于滤波器的状态估计。而FA-PF算法粒子在整体向高似然区域移动的同时，在低似然区域也合理的保留了部分粒子，使得这部分粒子所包含的状态信息得以在估计结果中体现，保证了粒子的多样性。

5 结 论

本文提出了一种基于萤火虫群优化的空间非合作目标相对导航粒子滤波算法，以改善标准粒子滤波的粒子贫化现象。文中给出了两星相对导航问题的状态模型和观测模型，分析了标准粒子滤波的缺陷，指出为解决粒子退化问题而引入的重采样技术会引起粒子贫化现象。结合萤火虫群优化思想，通过引入改进的萤火虫算法的荧光亮度和吸引度更新机制来解决粒子滤波的粒子贫化问题，并给出算法步骤。仿真结果表明，改进算法有效抑制了粒子贫化问题，明显提高了相对导航精度，有很高的工程应用价值。

（References）：

[1] 王楷, 汤亮, 李克行, 等. 航天器相对导航与控制技术的典型任务[J]. 空间控制技术与应用, 2016, 42(1): 7-12. Wang Kai, Tang Liang, Li Ke-xing. Application of relative navigation and control technology in specific space missions[J]. Aerospace Control and Application, 2016, 42(1): 7-12.

[2] 李文跃, 徐贵力, 周龙, 等. 空间非合作目标相对导航技术研究[J]. 航空兵器, 2012(3): 14-17. Li Wen-yue, Xu Gui-li, Zhou Long, et al. Research on mea- surement of relative poses between two non-cooperative spacecrafts[J]. Aero Weaponry, 2012(3): 14-17.

[3] Hablani H B, Tapper M L, Danabashian D J. Guidance and relative navigation for autonomous rendezvous in a circular orbit[J]. Journal of Guidance Control and Dynamics, 2012, 25(3): 553-562.

[4] Wu Jin-yuan, Fang Jian-cheng, Yang Zhao-hua. ASUKF based relative navigation method for mars probe using pulsar[J]. Chinese Journal of Scientific Instrument, 2013, 34(8): 1711-1716.

[5] 朱志宇. 粒子滤波算法及其应用[M]. 北京: 科学出版社, 2010: 27-29.

[6] Zhao Z N, Kumar M. An MCMC-based particle filter for multiple target tracking[C]//15thInternational Conference on Information Fusion. Singapore, 2012: 1676-1682.

[7] Sun Yun, Wang Guo-hong, Tan Shun-cheng, et al. A TBD algorithm for maneuvering stealthy target based on auxiliary particle filtering[J]. Electronics Optics & Control, 2013, 20(7): 28-31.

[8] Li Ming, Pang Bo, He Yong-feng, et al. Particle filter improved by genetic algorithm and particle swarm optimazation algorithm[J]. Journal of Software, 2013, 8(3): 666-672.

[9] Liu D, Liu G, Yu M. An improved FastSLAM framework based on particle swarm optimization and unscented particle filter[J]. Journal of Computational Information Systems, 2012, 8(7): 2859-2866.

[10] Li J S, Xi Z H, Zhao Y Q. Application of the Beidou/INS integrated navigation artificial fish-swarm particle filter [J]. Electronic Science and Technology, 2013, 26(6): 157-161.

[11] Yang X S. Firefly algorithm, stochastic test functions and design optimisation[J]. International Journal of Bio-Inspired Computation, 2010, 2(2): 78-84.

[12] Shan C F, Tan T N, Wei Y C. Real-time hand tracking using a mean shift embedded particle filter[J]. Pattern Recognition, 2007, 40(7): 1958 -1970.

Particle filter based on firefly algorithm optimization for relative navigation of non-cooperative target

ZHANG Da-li, XIA Hong-wei, MA Guang-cheng, WANG Chang-hong
(School of Astronautics, Harbin Institute of Technology, Harbin 150001, China)

The particle-filter resampling technology in the relative navigation of the non-cooperative target may cause the particle impoverishment phenomenon and decrease the relative navigation precision. To solve this problem, the operation mechanism of the firefly optimization algorithm is analyzed, and then an improved particle filter algorithm based on the firefly intelligent optimization algorithm is proposed. With the purpose of ensuring the diversity of particles and improving the integral quality of particle swarm, the improved algorithm enables the particle swarm to move towards the high likelihood region by optimizing the re-sampling process of particle filter, and reasonably remains some particles in low likelihood region at the same time. The simulation results show that, compared with the standard algorithm, the improved algorithm improves the navigation accuracy by about 39.35%, requires less quantity of the particles to achieve stable precision, and effectively restrain the problem of particle impoverishment.

firefly algorithm; particle filter; particle impoverishment; relative navigation

V448.22+4

A

1005-6734(2017)02-0269-06

10.13695/j.cnki.12-1222/o3.2017.02.025

2017-01-04；

2017-03-28

国家自然科学基金（61304108）

张大力（1991—），男，博士研究生，从事导航、滤波与控制研究。E-mail: 15b904016@hit.edu.cn

联 系 人：王常虹（1961—），男，教授，博士生导师，从事导航、制导与控制研究。E-mail: cwang@hit.edu.cn