强G-预不变凸函数

李 婷

(山西大学商务学院 基础教学部,太原 030031)

强G-预不变凸函数

李 婷

(山西大学商务学院 基础教学部,太原 030031)

主要以强G-预不变凸函数为研究对象，首先在中间点的G-预不变凸性下得到了G-预不变凸函数的一个判定定理，然后将已有文献的结果进行了推广，得到了在中间点的强G-预不变凸性下强G-预不变凸函数的两个重要的判定定理。

强G-预不变凸函数；严格G-预不变凸函数；半严格G-预不变凸函数

0 引言

在研究最优化问题时，凸性和广义凸性起着很重要的作用。近年来，国内外很多学者将凸函数不断进行推广，得到了一系列的广义凸函数及其相关成果，具体见参考文献[1-8],这些文献详细介绍了不变凸性、预不变凸性、强预不变凸性、G-预不变凸性、强G-预不变凸性等，并给出了这些广义凸函数的性质。

2011年，彭再云等在文献[8]中给出了强G-预不变凸函数的如下的一个判定定理。

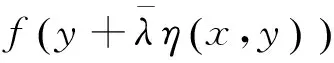
本文首先得到了半严格G-预不变凸函数是G-预不变凸函数的一个充分条件，然后将上述引理的结果进一步推广，得到了强G-预不变凸函数的另外两个判定定理。

1 基本知识

时上述不等式严格成立，即：

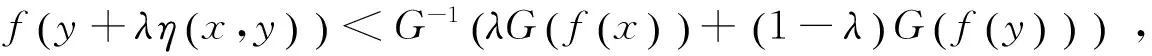
定义4[8]设集合K⊂Rn是关于η：Rn×Rn→Rn的不变凸集，f:K→R是定义K上的函数，称f是K上关于η的强G-预不变凸函数，如果存在连续递增函数：

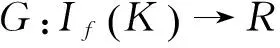
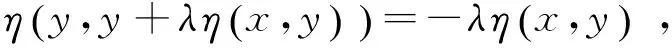
2 半严格G-预不变凸函数是G-预不变凸函数的一个充分条件

引理2.1 设G：R→R是一个连续实值函数，则G-1是递增函数当且仅当G也是递增函数。

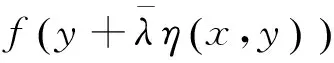
(1)

因为G单调递增，由引理2.1可知，G-1也是单调递增的。

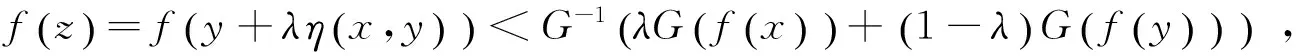
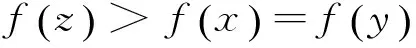
(2)

(3)

由f的半严格G-预不变凸性，引理2.1及(3)式可得：

上式与(2)式矛盾。

由f的半严格G-预不变凸性，引理2.1及(3)式可得：

上式与(2)式矛盾。故假设不成立，所以f是K上关于η的G-预不变凸函数。

3 强G-预不变凸函数的两个判定定理

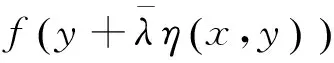
(4)

则f是K上关于η的强G-预不变凸函数。

(5)

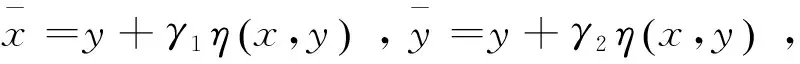
(6)

由条件C可得：

(7)

(8)

由(4)和(7)式可得：

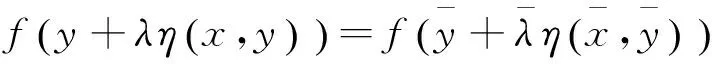
(9)

又由(6)式有：

(10)

所以，由(8)、(9)及(10)式可得：

于是，f是K上关于η的强G-预不变凸函数。

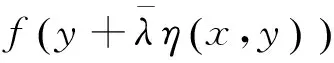
(11)

则f是K上关于η的强G-预不变凸函数。

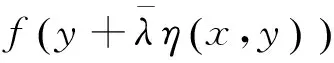
(12)

由定理2.1及(12)式知f是K上关于η的G-预不变凸函数，从而由引言中的引理得，f是K上关于η的强G-预不变凸函数。

[1]CravenBD.Invexfunctionsandconstrainedlocalminima[J].BulletinoftheAustralianMathematicalSociety, 1981, 24(3):357-366.

[2]WeirT,MondB.Preinvexfunctionsinmultipleobjectiveoptimization[J].JournalofMathematicalAnalysis&Applications, 1988, 136(1):29-38.

[3] 颜丽佳, 刘芙萍. 强预不变凸函数[J]. 重庆师范大学学报(自然科学版), 2005, 22(1):11-15.

[4]SchaiblesT,ZiembaWT.Generalizedconcavityinoptimizationandeconmics[M].London:AcademicPress, 1981.

[5]AntczakT.G-pre-invexfunctionsinmathematicalprogramming[J].JournalofComputational&AppliedMathematics, 2008, 217(1):212-226.

[6]AntczakT.NewoptimalityconditionsanddualityresultsofGtypeindifferentiablemathematicalprogramming[J].NonlinearAnalysis, 2007, 66(7):1617-1632.

[7]LuoHZ,WuHX.OntherelationshipsbetweenG-preinvexfunctionsandsemistrictlyG-preinvexfunctions[J].JournalofComputational&AppliedMathematics, 2008, 222(2):372-380.

[8] 彭再云, 房效亮, 赵勇. 强G-预不变凸函数[J]. 重庆师范大学学报(自然科学版), 2011, 28(6):7-10+18.

责任编辑：程艳艳

StrongG-PreinvexFunctions

LITing

(FundamentalTeachingDepartment,BusinessCollegeofShanxiUniversity,Taiyuan030031,China)

Taking strongG-preinvexfunctionastheresearchobject,thispaperobtainsajudgingtheoremofG-preinvexfunctiononthemiddlepointofG-preinvexity,andthengeneralizestheresultsoftheexistedliterature,finally,obtainstwoimportantjudgingtheoremsofstrongG-preinvexfunctiononthemiddlepointofstrongG-preinvexity.

strongG-preinvexfunction；strictG-preinvexfunction；semi-strictG-preinvexfunction

2017-02-18

山西省教育科学“十三五”规划课题(GH—16713)；山西大学商务学院科研项目(2016027)

李婷(1981-)，女，山西永济人，讲师，硕士，主要从事最优化理论及应用方面研究。

O

A

1009-3907(2017)04-0025-04