楔形变截面双模量梁弯曲变形时的解析解

谭丽菲,吴晓,罗佑新

(1.常德市规划建筑设计院有限责任公司,湖南 常德,415000;2.湖南文理学院 机械工程学院,湖南 常德,415000)

楔形变截面双模量梁弯曲变形时的解析解

谭丽菲1,吴晓2,罗佑新2

(1.常德市规划建筑设计院有限责任公司,湖南 常德,415000;2.湖南文理学院 机械工程学院,湖南 常德,415000)

推导出了楔形矩形变截面双模量梁的截面高度表达式,利用静力平衡方程确定了楔形矩形变截面双模量梁弯曲时的中性层位置。采用弹性理论建立了楔形矩形变截面双模量梁的弯曲微分方程,推导出了外载荷作用下梁的挠度表达式。通过算例,讨论了楔度比、长高比、剪切效应对楔形矩形变截面双模量梁弯曲变形时挠度的影响。结果表明:随着楔度比的增大,梁的弯曲挠度逐渐减小;随着长高比的增大,双模量材料简支梁、悬臂梁中点的弯曲挠度均逐渐增大,各向同性悬臂梁的中点弯曲挠度也逐渐增大;对于拉压弹性模量相差较大的双模量材料梁的弯曲挠度计算,用经典材料力学理论计算是不合适的,应采用双模量材料力学理论进行分析计算。

楔形;变截面;双模量;梁;弯曲变形

拉压弹性模量不同是双模量材料具有的典型特征。文献[1-2]研究了非线性材料梁的弯曲应力计算;文献[3]研究了基于敏度分析的不同模量桁架正反问题求解;文献[4]研究了基于敏度分析的拉压不同模量桁架问题的数值分析;文献[5]研究了拉压模量不同弹性物质本构关系;文献[6]初步建立了不同模量弹性理论;文献[7]研究了不同拉压模量及软化特性材料的柱形孔扩张问题的统一解;文献[8-10]研究了双模量梁的变形问题。由于楔形变截面杆作为承载结构,已在工程实际中得到广泛应用,因此本文采用弹性理论研究了楔形变截面梁的弯曲变形。

1 中性层的确定

以图1所示楔形矩形变截面双模量梁为例,假设变截面梁宽为b,梁高变化高度为H(x),可知其任意截面高度表达式为H(x)=H1(1 −εx/l),式中,β=H0/H1＜1为楔度比,ε=1 -β＜1。

双模量梁纯弯曲时,会形成拉压弹性模量不同的拉伸区和压缩区,由材料力学理论可知,双模量梁弯曲时,拉伸区及压缩区的应力表达式为σ1′=E1y/ρ和σ2′=E2y/ρ。式中:E1、E2分别为双模量梁拉伸区、压缩区的弹性模量;ρ为双模量梁弯曲时,曲率中心至中性层的距离;σ1′、σ2′分别为双模量梁的拉应力和压应力;y为双模量梁横截面内与中性轴垂直的轴的坐标,横轴与中性轴重合。

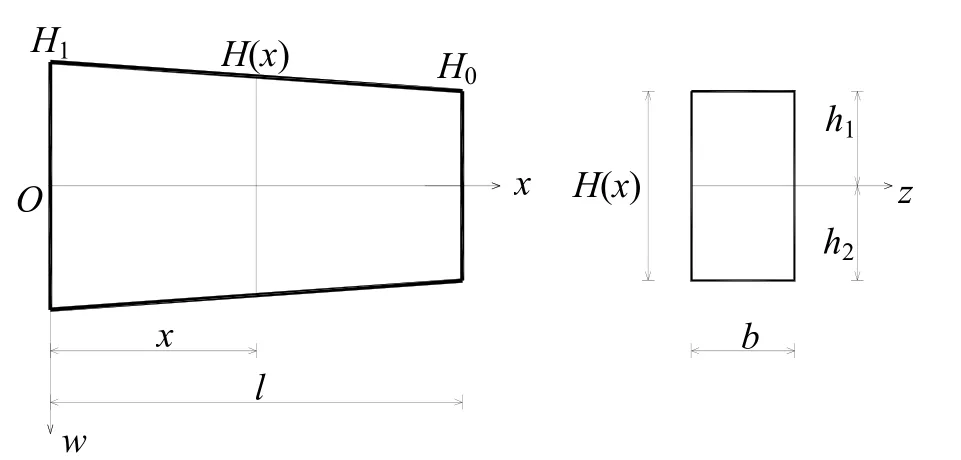
图1 楔形矩形变截面双模量梁

由材料力学知识可知,双模量梁弯曲时,横截面轴向静力方程为拉伸区高度h1与压缩区高度h2关系为H(x)=h1+h2。因此,由于曲率半径ρ及梁高H(x)均是轴向坐标的函数,与纵坐标无关可求得

2 梁弯曲挠曲线方程

由弹性理论可知,双模量梁在外载荷作用下,梁微段平衡方程、应力与应变的本构关系为

式中,Fxi、Fyi分别为作用在梁微段上的外力,并

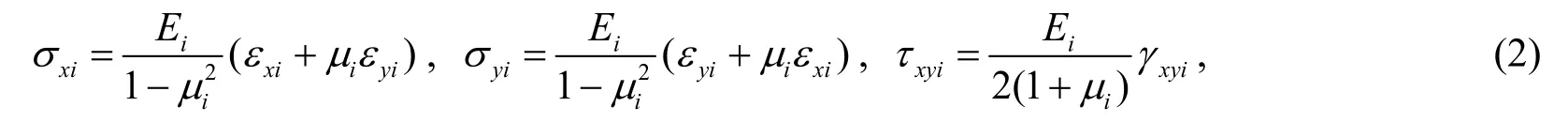
以图1所示矩形双模量梁为例,假设变形后梁截面保持平面,但可以不再垂直中性轴线。这样,梁的中性轴线挠度w(x)为梁的垂直位移,而水平方向位移为y的一阶项,即u(x,y)=−yθ(x),式中,θ(x)为横截面在中性轴线处的转角。

由于一维梁理论忽略了横向挤压应力,即σyi=0时,可把式(1)及(2)化为如下形式:

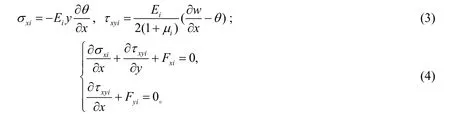
假设在图1所示楔形变截面双模量梁上作用有沿梁长l分布的均布载荷q0,可以求得

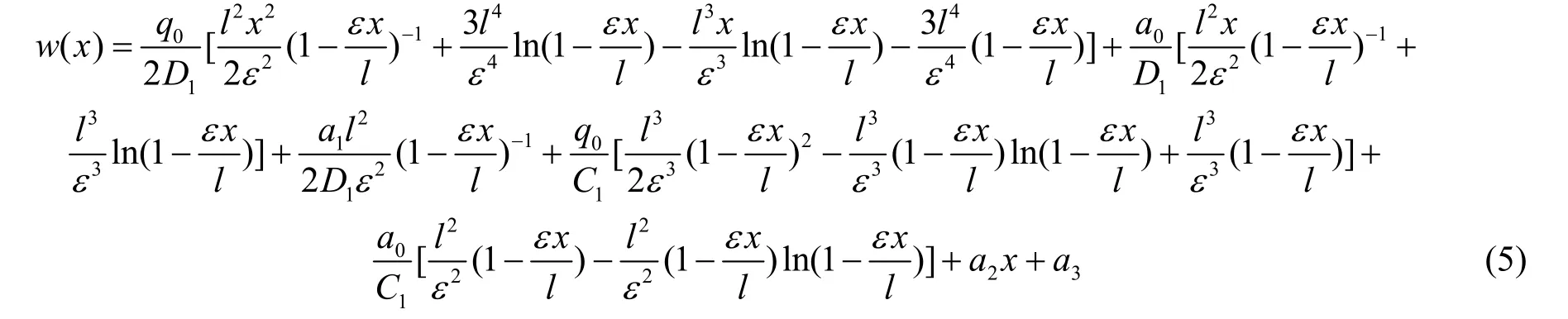
对于其它支承的楔形变截面双模量梁在外载荷作用下的挠曲线方程,利用θ(x)及w(x)的表达式,且结合边界条件同样可以方便求得。

3 算例分析

下面利用式(5)、(8)、(10),计算楔形变截面双模量简支梁、双模量悬臂梁上作用有沿梁长分布的均布载荷q0时,楔度比、剪切效应对楔形矩形变截面双模量梁弯曲变形时梁中点挠度的影响。双模量梁材料参数及截面尺寸为E1=113 GPa,E2=145 GPa,μ1=0.22,μ2=0.29,b=50 mm,H1=100 mm。假设沿双模量梁长作用有均布载荷q0=100 kN/m。参阅文献[11]平面应力问题有剪切系数k=8/9。具体计算结果列在表1～6中,表1～6中括号内数字为不考虑剪切变形时梁中点的挠度。

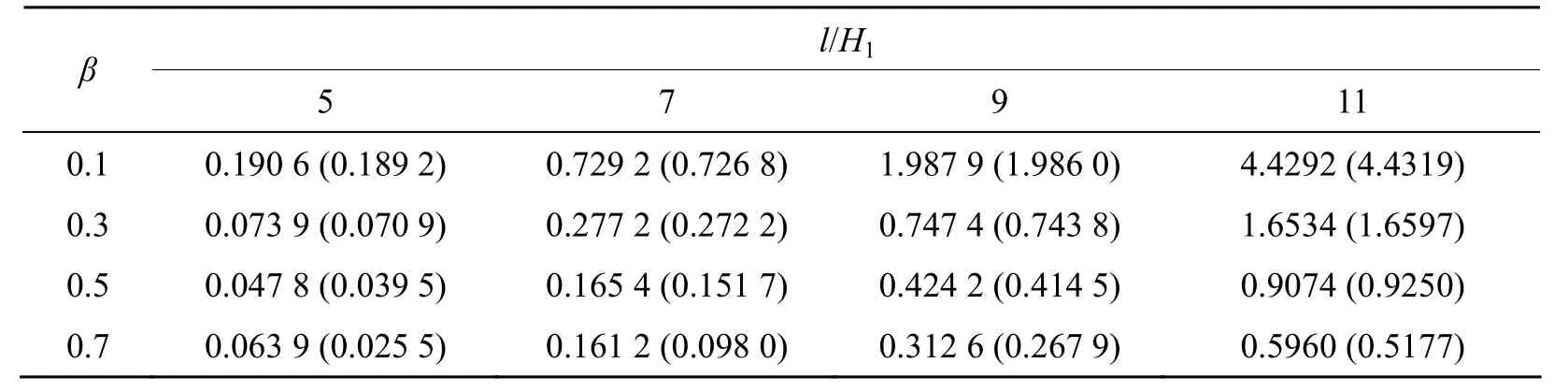
表1E1=113 GPa,E2=145 GPa时,双模量简支梁中点挠度 /mm

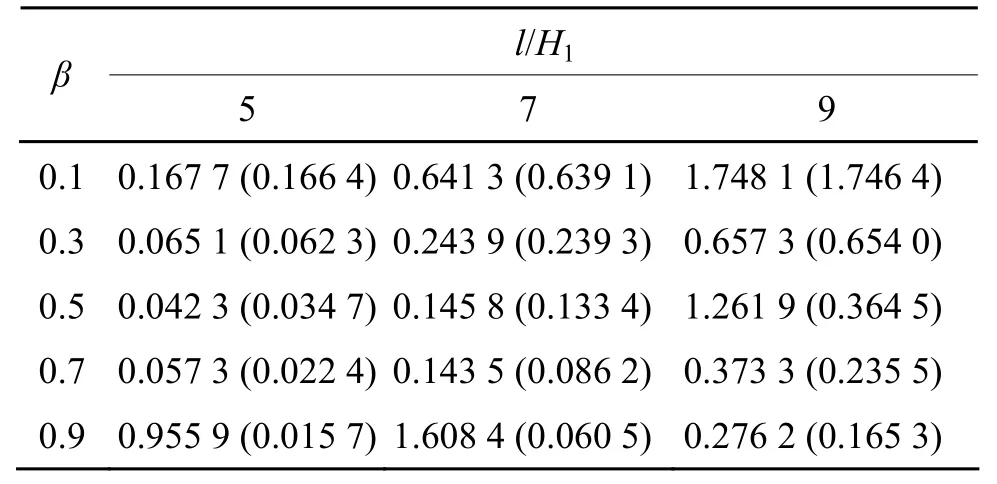
表2E1=E2=145 GPa时,各向同性简支梁中点挠度/mm

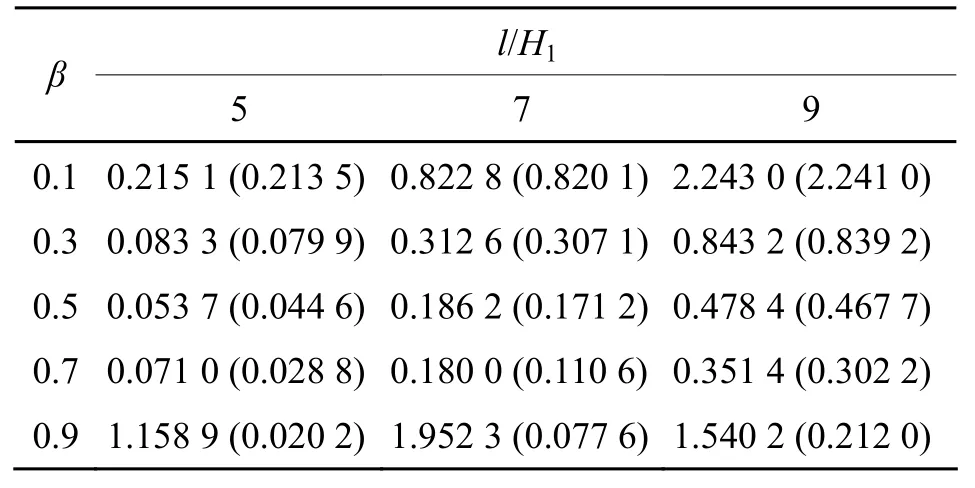
表3E1=E2=113 Gpa时,各向同性简支梁中点挠度/mm

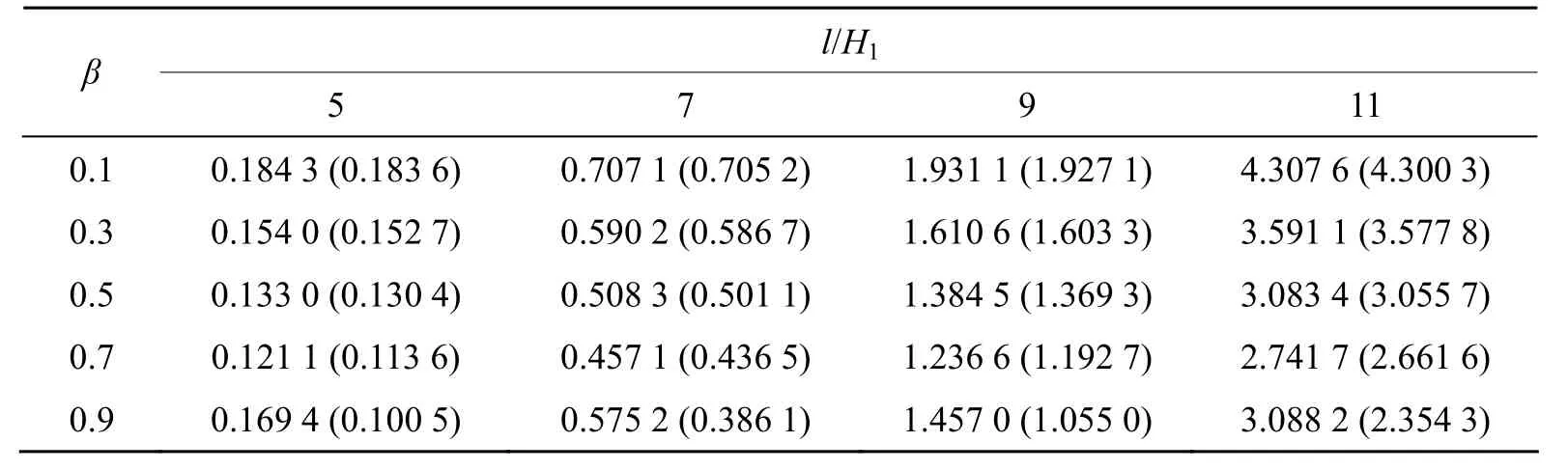
表4E1=113 GPa,E2=145 GPa时,双模量悬臂梁中点挠度 /mm

表5E1=E2=145 GPa时,各向同性悬臂梁中点挠度/mm

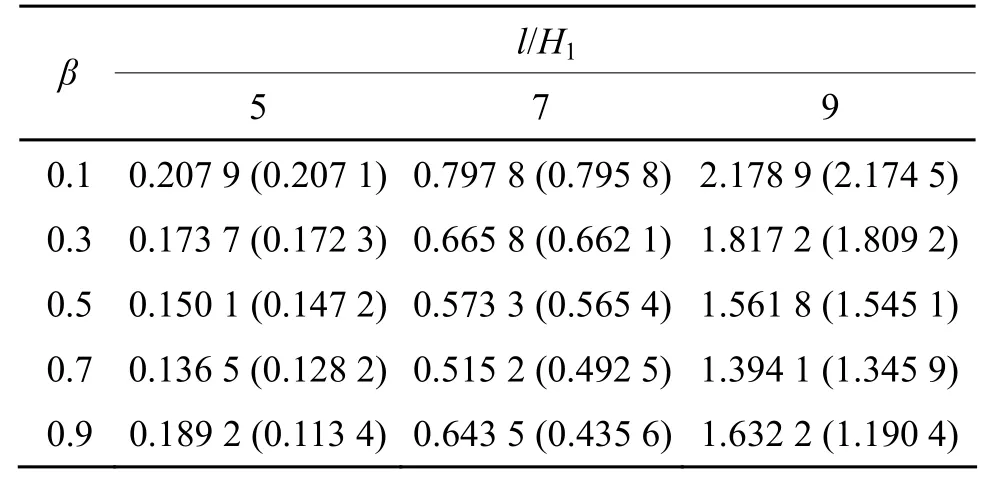
表6E1=E2=113 GPa时,各向同性悬臂梁中点挠度/mm

分析表1～6结果可知,把双模量材料梁作为各向同性梁进行挠度计算,所得误差均在10%以上。所以,对于拉压弹性模量相差较大的双模量材料梁的弯曲挠度计算,采用经典材料力学理论计算是不合适的,应该采用双模量材料力学理论进行分析计算。

随着楔度比β的增大,梁的弯曲挠度逐渐减小。随着长高比l/H1的增大,双模量材料简支梁、悬臂梁中点的弯曲挠度均逐渐增大,各向同性悬臂梁的中点弯曲挠度也逐渐增大。对于各向同性简支梁,当0.1 ＜β＜0.9,且0 ＜l/H1≤ 7时,随着长高比l/H1的增大,各向同性简支梁中点弯曲挠度也逐渐增大;当β≥ 0.9,且l/H1≥ 7时,随着长高比l/H1的增大,各向同性简支梁中点弯曲挠度逐渐减小。

对于双模量材料简支梁考虑剪切变形时,当l/H1≤ 9时,考虑剪切变形时梁中点的弯曲挠度均大于不考虑剪切变形时梁中点的挠度。当l/H1＜9,β＜0.7时,考虑剪切变形时中点的弯曲挠度均小于不考虑剪切变形时梁中点的挠度。对于双模量材料悬臂梁,考虑剪切变形时梁中点的弯曲挠度均大于不考虑剪切变形时梁中点的挠度。对于双模量材料梁,当β＞ 0.7时即使长高比l/H1=11,考虑剪切变形时梁中点弯曲挠度与不考虑剪切变形时梁中点挠度的误差超过5%。

4 结论

(1)随着楔度比β的增大,梁中点的弯曲挠度逐渐减小。随着长高比l/H1的增大,双模量材料简支梁、悬臂梁中点的弯曲挠度均逐渐增大,各向同性悬臂梁的中点弯曲挠度也逐渐增大。

(2)对于双模量材料悬臂梁,考虑剪切变形时,中点的弯曲挠度均大于不考虑剪切变形时梁中点的挠度。对于双模量材料简支梁考虑剪切变形时,当l/H1≤9时,考虑剪切变形时梁中点的弯曲挠度均大于不考虑剪切变形时梁中点的挠度。当l/H1＞9,β＜0.7,考虑剪切变形时,中点的弯曲挠度均小于不考虑剪切变形时梁中点的挠度。

(3)对于拉压弹性模量相差较大的双模量材料梁的弯曲挠度计算,采用经典材料力学理论进行双模量梁的弯曲挠度计算分析是不合适的,应该采用双模量材料力学理论进行分析计算。

[1]张大伦,李宗榕.材料力学(上册)[M].上海:同济大学出版社,1987:378-379.

[2]S 铁摩辛柯.J 盖尔.材料力学[M].北京:科学出版社,1990:237-242.

[3]张晓月.基于敏度分析的不同模量桁架正反问题求解[D].大连:大连理工大学,2008.

[4]杨海天,张晓月,何宜谦.基于敏度分析的拉压不同模量桁架问题的数值分析[J].计算力学学报,2011,28(2):237−242.

[5]蔡来生,俞焕然.拉压模量不同弹性物质的本构[J].西安科技大学学报,2009,29(1):17-21.

[6]阿巴尔楚米扬,著.不同模量弹性理论[M].邬瑞锋,张允真,译.北京:中国铁道出版社,1986:11-22.

[7]罗战友,夏建中,龚晓南.不同拉压模量及软化特性材料的柱形孔扩张问题的统一解[J].工程力学,2008,25(9):79-84.

[8]吴晓,黄翀,孙晋.线性分布载荷作用下双模量简支梁的Kantorovich解[J].中南大学学报(自然科学版),2013,44(5):2 082-2 087.

[9]吴晓,杨立军,黄翀,等.双模量悬臂梁在线性分布荷载作用下的 Kantorovich解[J].中南大学学报(自然科学版),2014,45(1):306-311.

[10]吴晓,杨立军,黄志刚.利用剪切效应原理计算双模量材料的性能参数解[J].中南大学学报(自然科学版),2014,45(2):609-614.

[11]Timoshenko S P.On the transverse vibrations of bars of uniform cross section [J].Philosophical Magazine,1922,43(6):122-131.

(责任编校:江河)

Analytical solution of tapered bimodulous beam during bending deformation

Tan Lifei1,Wu Xiao2,Luo Youxin2
(1.Changde Planning and Architectural Design Institute Co Ltd,Changde 415000,China;2.College of Mechanical Engineering,Hunan University of Arts and Science,Changde 415000,China)

The equations of cross height for tapered bimodulous beam are deduced and the static equations are used to determine the location of neutral axis in tapered bimodulus beam.Using the elastic theory,the bending differential equation for tapered bimodulous beam is established and deflection expression for beam under external load is deduced.By analysis of examples,that the effect of wedge ratio,length-height ratio and shear effect on the deflection of tapered bimodulous beam during bending deformation are discussed.The results show that with the increasing of wedge ratios,the bending deflection decreases,and with the increasing of length-height ratios,the bending deflection in the midpoint for bimodulous simply supported beam,cantilevers and cantilevers with isotropic material increase.Calculation of bending deflection for bimodulous beam is inappropriate by the method of the classic mechanic theory when elasticity modulu of tension and compression is large.The bimodulus materials theory is suitable to calculate the bending deflection of bimodulous beam.

tapered;variable cross section;bimodulous;beam;bending deflection

O 343.5

A

1672-6146(2017)02-0090-05

吴晓,wx2005220@163.com。

2017-04-01

湖南省科技计划项目(2011SK3145);湖南“十二五”重点建设学科项目(湘教发[2011]76号);湖南省自然科学基金(2015JJ6073)。

10.3969/j.issn.1672-6146.2017.02.021