下伏空洞顶板承载力的计算方法综述
尹君凡,雷勇,陈秋南
(湖南科技大学 岩土工程稳定控制与健康监测湖南省重点实验室,湖南 湘潭,411201)
下伏空洞顶板承载力的计算方法综述
尹君凡,雷勇,陈秋南
(湖南科技大学 岩土工程稳定控制与健康监测湖南省重点实验室,湖南 湘潭,411201)
顶板承载力问题主要存在于矿山开采、采空区以及岩溶区工程建设中。将应用于下伏空洞顶板承载力计算的理论方法归纳为弹性理论和极限分析方法2种,其中极限分析方法包括极限平衡法和极限分析上限法。对于具体问题的求解,利用弹性理论时,关键是选取合理的力学模型;利用极限分析方法时,关键是给出恰当破坏模式的假定。目前对于偏心荷载作用下的顶板破坏机理研究较少,尚没有成熟的理论计算方法,该方面的研究有待加强。
空洞顶板;承载力;弹性理论;极限分析方法;破坏判据
随着我国矿山开采活动频率的不断增加,采空区的增多以及岩溶区桥梁工程建设的不断推进,巷道顶板、采空区顶板以及溶洞顶板等下伏空洞顶板承载力问题一直备受关注。国内学者对下伏空洞顶板承载力的计算进行了大量的研究,且提出了一些理论计算方法,但尚未有学者针对此类计算方法进行系统总结。本文主要梳理并总结了国内学者对下伏空洞顶板承载力的计算方法,对各种方法的计算思路和特点进行了阐述。
1 弹性理论
弹性理论的基本思路是先将空洞顶板简化为某种力学模型,再由弹性理论得到顶板岩层内的应力分布,最后选择适当控制条件(破坏判据),得到顶板的最大承载力。该方法的主要力学模型有双向受压无限板孔模型、厚板模型、薄板模型及简支梁模型。
1.1 双向受压无限板孔模型
刘之葵等[1]将圆形和椭圆形溶洞的受力简化为双向受压无限板孔的平面应力分布问题,其模型如图1所示。由已有的齐尔西解答,得到溶洞周围的应力分布,并引进Griffith强度准则,得到溶洞顶板的承载力。
1.2 厚板模型
基于Reissner厚板理论,祝方才等[2]将浅埋空区顶板简化为轴对称圆板(图2(a)),分别推导了以拉、剪破坏为控制条件的顶板承载力。王树仁等[3]将采空区顶板简化成四边简支矩形板(图 2(b)),考虑了施工动荷载,得到了以抗拉强度为控制条件的采空区顶板承载力。武崇福等[4]以抗拉强度为控制条件,得到了四边固支(图2(c))和四边铰支矩形板模型下的岩溶及采空区顶板承载力。
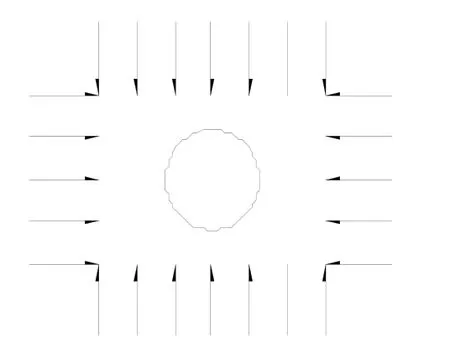
图1 双向受压无限板孔模型

图2 厚板模型
基于 Volasov厚板理论,赵国彦等[5]以拉应力极限强度理论为破坏判据,将海下开采场顶板简化成四边固支和简支模型,分别得到了其承载力。
1.3 薄板模型
针对溶洞顶板承载力问题,王华斌等[6]基于薄板模型,将溶洞顶板简化为固支和简支的圆板和矩形板,由弹性理论推导了4种模型下的最大应力。并以Hoek-Brown强度准则为破坏判据,得到了剪切和冲切破坏模式下的顶板承载力。
针对采场顶板承载力问题,李肖音、王新丰等[7-8]基于薄板模型,将采场顶板简化为固支、简支的矩形板等不同的力学模型,利用瑞利-里兹法,求得了采场顶板的承载力。
1.4 简支梁模型
赵明华、蒋冲等[9-10]基于简支梁模型(图 3(a)),由弹性理论导出了溶洞顶板岩层的应力分布,并以修正的Mohr-Clomb准则为破坏判据,得到了顶板承载力。马俊等[11]基于简支梁模型,由弹性理论推导了溶洞顶板的应力分布,并引入三维Hoek-Brown强度准则,结合非概率可靠性分析理论对溶洞顶板的稳定性进行了分析。
江学良等[12-13],基于改进的简支梁模型(图 3(b)),考虑了水平应力,利用瑞利-里兹法,以抗拉强度为控制条件,得到了溶洞顶板承载力,同时考虑了裂隙密度对顶板承载力的影响。之后又在此基础上得到了弹性状态、拉伸屈服、压缩屈服以及拉压屈服并存下的顶板承载力。
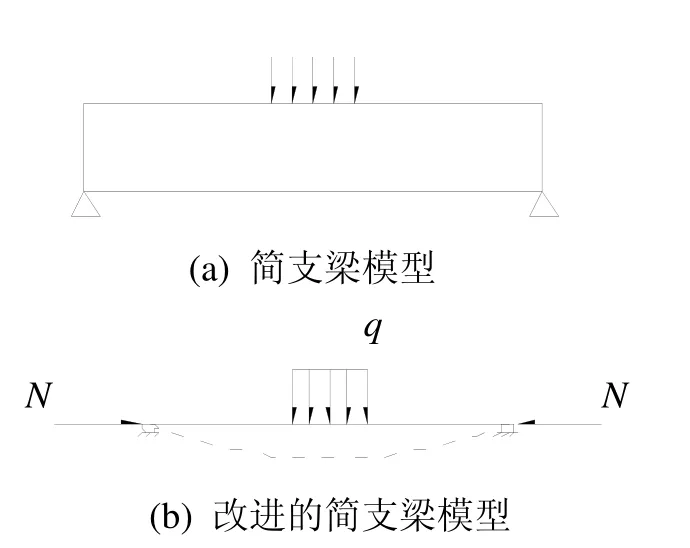
图3 简支梁模型
除以上模型外,李倩倩等[14]将城市浅部地层椭圆形空洞视为深埋问题,利用复变函数理论对其稳定性进行了分析。
综上可以发现,利用弹性理论求解顶板的承载力时,首先要求出顶板的内力,此时要用到顶板材料的本构关系,因此,可以认为该计算方法是严格意义上的力学解法。在处理具体的工程问题时,能否得到满意的结果,关键看力学模型的假定能否反映工程特点。
2 极限分析方法
极限分析方法自提出以来已有百年的发展历史,其包括极限平衡法、滑移线场法和极限分析上、下限法。针对下伏空洞顶板极限承载力问题,国内很多学者利用极限平衡法和极限分析上限法做了一些有益的尝试。
2.1 极限平衡法
极限平衡法的基本思路是根据工程经验、实际情况或模型试验结果等,假定某种破坏模式,分析顶板处于极限状态时,该破坏模式下顶板内力与外力的静力平衡条件,并基于某种控制条件(破坏判据),得出顶板的极限承载力。
赵明华等[15-18]基于极限平衡法,针对岩溶地区溶洞顶板的承载力问题做了大量的研究。其基本思路为:假定溶洞顶板为一固支的刚性底板(图 4),基于处于极限平衡状态时溶洞顶板的静力平衡条件,分别对冲切、剪切和弯拉破坏模式进行分析。通过借助已有的混凝土板抗冲切研究成果[15],或是将破坏面上的拉应力与剪应力分开单独考虑,并以抗拉、抗剪强度为控制条件[16],或引入Griffith、修正的莫尔[17]以及Hoek-Brown强度准则[18]等方法,得出溶洞顶板的极限承载力。
此外,在极限平衡分析模型基础上,赵明华、曹文贵等[19-20]将模糊集理论引入溶洞顶板极限承载力的分析中,建立了溶洞顶板模糊极限平衡分析的模型。曹文贵等[21]将Information-Gap理论应用到溶洞顶板的稳定性分析中,龚先兵等[22]采用非概率可靠性理论,对溶洞顶板的稳定性进行了分析。
可以发现,极限平衡法不需要引入本构方程,只需满足极限状态时的平衡条件和屈服条件,因而该方法不是严格意义上的力学解法。但是对于实际工程,该方法能够满足工程所需精度,且计算方便,因此在岩土工程设计中应用广泛。
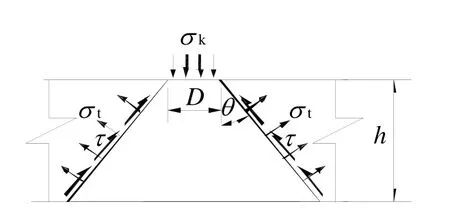
图4 极限平衡理论的冲切体破坏模式
2.2 极限分析上限法
极限分析上限法的基本思路:假定顶板发生某种可能的破坏模式,并在此破坏模式下,当顶板处于极限状态时,基于某种破坏判据,由外力做功功率与内力耗散功率相等得出极限外荷载,并通过求偏导等方法求出极限外荷载的极小值,即顶板极限承载力的上限解。
2.2.1 基于薄板模型的塑性破坏模式
谭云亮、戴国兴、柏建彪、黄耀光等[23-27]将采场顶板简化为不同支承情况的矩形板(图 5),计算其极限承载力问题。采用塑性极限分析法,通过求偏导的方法解出各种支承条件下板的最佳破损机构(在所有可能的破损机构中,极限荷载最小时所对应的破损机构)以及相应的极限承载力。

图5 基于薄板模型的塑性破坏模式
2.2.2 基于板模型的冲切破坏模式
赵明华、雷勇等[28-29]针对溶洞顶板的极限承载力问题,假定溶洞顶板为一固支的刚性底板,在冲切破坏模式下,假定冲切体是一个母线为未知曲线的旋转体(图 6),利用变分法原理以及求偏导的方法,分别得到了以Griffith和Hoek-Brown强度准则为破坏判据的溶洞顶板冲切体的母线形式以及相应的极限承载力。
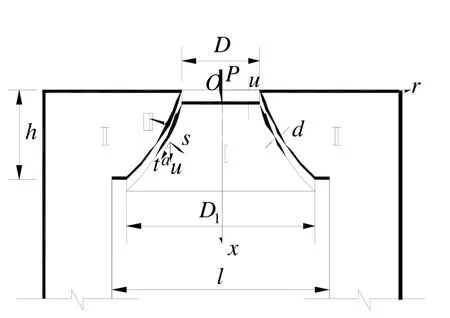
图6 冲切体破坏模式
刘辉等[30]针对空洞上方浅基础地基承载力问题,利用极限分析上限法分析了空洞大小以及顶板厚度对破坏模式和承载力的影响。
可以发现,极限分析上限法与极限平衡法一样,需要满足极限状态时的平衡条件以及屈服条件,只不过此时的平衡条件是功能方程表述的平衡条件。另外,极限分析上限法还需满足假定的破坏模式下所能容许的机动条件,该机动条件仅为运动学上所许可的条件。同极限平衡法一样,极限分析上限法无需引入顶板材料的本构关系,不是严格意义上的力学解法,但其能够满足工程所需精度,因此,也是一种有效的分析方法。
总的来说,应用于下伏空洞顶板承载力计算的理论方法包括弹性理论和极限分析方法2种,其中极限分析方法又包括极限平衡法和极限分析上限法。应用弹性理论计算顶板承载力时,可以认为其是严格意义上的力学解法,但实际问题与简化的力学模型有时可能有较大的差别,运用弹性理论得出的结果将无法合理地反应实际情况。而且其计算程序往往较复杂,这将严重阻碍其在实际工程中的应用。应用极限分析方法解决工程问题时,计算程序简便,因其是直接基于破坏模式的理论计算方法,所以只要破坏模式选取恰当,就能够得到合理的结果,在工程实践中有很大的应用价值。极限分析上限法相比较于极限平衡法,不仅有简便的计算程序,而且更能反映真实的破坏情况,值得在实践中推广。
以上所提及的计算顶板承载力的计算方法,均是针对轴对称荷载作用下的顶板承载力。目前对于偏心荷载作用下的顶板破坏机理研究较少,除了少量的室内试验和基于数值方法方面的研究[31-33],尚没有提出相应的理论计算方法。在具体工程实践中,不可避免地会遇到偏心荷载作用的情况,因此,今后有必要加强对偏心荷载作用下的顶板破坏机理的研究。
3 结论
本文较详细地总结了国内学者对下伏空洞顶板承载力的计算方法,并对各种方法的计算思路和特点进行了分析,得到以下观点。
(1)应用于下伏空洞顶板承载力计算问题的理论方法主要有弹性理论和极限分析方法2种,其中极限分析方法包括极限平衡法和极限分析上限法。
(2)对于具体的问题的求解,在选择合适控制条件的基础上,利用弹性理论时,关键是选取合理的力学模型,利用极限分析方法时,关键是给出恰当的破坏模式假定。
(3)极限分析方法计算过程简便,在实际工程中有广阔的应用前景。其中基于功能原理的极限分析上限法,其相对于极限平衡法更能反映真实的极限状态,因此,在工程实践中应是更值得关注的方法。
(4)目前对于偏心荷载作用下的顶板破坏机理研究较少,尚没有提出相应的理论计算方法。当前应对偏心荷载作用下的顶板破坏机理进行重点研究。
[1]刘之葵,梁金城,朱寿增,等.岩溶区含溶洞岩石地基稳定性分析[J].岩土工程学报,2003,25(5):629-633.
[2]祝方才,曹平,万文.基于轴对称厚板模型的浅埋空区顶板安全厚度[J].采矿与安全工程学报,2006,23(1):115-118.
[3]王树仁,贾会会,武崇福.动荷载作用下采空区顶板安全厚度确定方法及其工程应用[J].煤炭学报,2010,35(8):1 263-1 268.
[4]武崇福,赵宇.基于厚板理论确定岩溶及采空区路基岩层顶板安全厚度[J].公路交通科技,2014,31(10):32-37.
[5]赵国彦,周士祥.基于厚板理论的滨海开采顶板安全厚度确定[J].中国地质灾害与防治学报,2015,26(4):60-66.
[6]汪华斌,刘志峰,赵文锋,等.桥梁桩基荷载下溶洞顶板稳定性研究[J].岩石力学与工程学报,2013,3(2):3 650-3 657.
[7]李肖音,高峰,钟卫平.基于板模型的采场顶板破断机理分析[J].采矿与安全工程学报,2008,25(2):180-183.
[8]王新丰,高明中.变长工作面采场顶板破断机理的力学模型分析[J].中国矿业大学学报,2015,44(1):36-45.
[9]赵明华,单联君,曹文贵.基于岩石统计损伤理论的嵌岩桩竖向承载力计算[J].中南公路工程,2004,29(4):6-9.
[10]蒋冲,赵明华,胡柏学,等.路基溶洞顶板稳定性影响因素分析[J].公路工程,2009,34(1):5-9.
[11]江学良,曹平,杨慧,等.水平应力与裂隙密度对顶板安全厚度的影响[J].中南大学学报(自然科学版),2009,40(1):211-216.
[12]江学良,曹平,杨慧.地下空区顶板改进梁模型的弹塑性分析[J].中南大学学报(自然科学版),2012,43(9):3 659-3 664.
[13]马俊,王星华.基于 Hoek-Brown 强度准则桩端溶洞顶板非概率可靠性分析[J].地下空间与工程学报,2014,10(5):1 146-1 150.
[14]李倩倩,张顶立,房倩.含空洞地层初始破坏的复变函数解析研究[J].岩土工程学报,2014,36(11):2 110-2 117.
[15]赵明华,曹文贵,何鹏祥.岩溶及采空区桥梁桩基桩端岩层安全厚度研究[J].岩土力学,2004,25(1):64-68.
[16]赵明华,陈昌富,曹文贵,等.嵌岩桩桩端岩层抗冲切安全厚度研究[J].湘潭矿业学院学报,2003,18(4):41-45.
[17]赵明华,张锐,胡柏学,等.岩溶区桩端下伏溶洞顶板稳定性分析研究[J].公路交通科技,2009,26(9):13-17.
[18]赵明华,周磊,雷勇.基于H-B强度理论的桩端岩层安全厚度确定[J].湖南大学学报(自然科学版),2010,37(6):1-5.
[19]赵明华,程晔,曹文贵.桥梁基桩桩端溶洞顶板稳定性的模糊分析研究[J].岩石力学与工程学报,2005,24(8):1 376-1 383.
[20]曹文贵,颜艳芬,张永杰.基桩桩端岩溶顶板稳定性模糊能度可靠性分析方法[J].岩石力学与工程学报,2009,28(1):88-94.
[21]曹文贵,李媛,翟友成.基于 Info-Gap 理论的基桩下伏岩溶顶板稳定性的主动分析方法[J].岩石力学与工程学报,2013,32(2):393-400.
[22]龚先兵,赵明华,张永杰.桩端下伏溶洞顶板稳定非概率可靠性分析方法[J].湖南大学学报(自然科学版),2011,38(1):13-17.
[23]谭云亮,蒋金泉.采场坚硬顶板断裂步距的板极限分析[J].山东矿业学院学报,1989,8(3):21-26.
[24]戴兴国,钱鸣高.老顶岩层破损与来压的理论分析[J].矿山压力与顶板管理,1992(3):7-11.
[25]戴兴国,钱鸣高.极限分析与老顶初次来压步距计算[J].中国矿业大学学报,1993,22(1):17-23.
[26]柏建彪,耿欧,马中国.巷道顶板锚杆支护机理的极限载荷分析[J].矿山压力与顶板管理,1999(3/4):164-166.
[27]黄耀光,浦海.不同边界下的坚硬顶板极限承载分析及破断距确定[J].煤矿开采,2012,17(2):12-16.
[28]赵明华,雷勇,张锐.岩溶区桩基冲切破坏模式及安全厚度研究[J].岩土力学,2012,33(2):524-530.
[29]雷勇,陈秋南,马缤辉.基于极限分析的桩端岩层冲切分析[J].岩石力学与工程学报,2014,33(3):631-638.
[30]刘辉,杨峰,阳军生.空洞上方浅基础地基破坏模式与极限承载力分析[J].岩土力学,2010,31(11):3 373-3 378.
[31]王华牢,张鹏,李宁.岩溶洞穴对嵌岩单桩承载力的影响研究[J].西安理工大学学报,2010,26(1):31-36.
[32]张慧乐,马凛,张智浩,等.岩溶区嵌岩桩承载特性影响因素试验研究[J].岩土力学,2013,34(1):92-100.
[33]张慧乐,张智浩,王述红,等.岩溶区嵌岩桩的试验研究与分析[J].土木工程学报,2013,46(1):92-103.
(责任编校:江河)
Summary about researches on the calculation method for the bearing capacity of cave roof
Yin Junfan,Lei Yong,Chen Qiunan
(Hunan Provincial Key Laboratory of Geotechnical Engineering for Stability Control and Health Monitoring,Hunan University of Science and Technology,Xiangtan 411201,China)
The problem of bearing capacity of roof mainly exists in the mining,old mine goaf and construction in karst area.Two theory methods,elastic theory and limit analysis method,are applied to evaluate the bearing capacity of cave roof.Thereinto,limit analysis methods include limit equilibrium method and the upper bound method of limit analysis.To solve a certain problem,it is crucial to choose the mechanical model properly when elastic theory is used.At present,few researches and mature theoretical calculation methods on failure mechanism of cave roof under off-centre load are reported,and research of this respect needs to be strengthened.
cave roof;bearing capacity;elastic theory;limit analysis method;failure evaluation criterion
TU 473
A
1672-6146(2017)02-0068-05
尹君凡,schrodingers_box@163.com。
2016-12-28
国家自然科学基金(51208195);岩土工程稳定控制与健康监测湖南省重点实验室开放基金(E21618)。
10.3969/j.issn.1672-6146.2017.02.016

