孔隙水压力作用下抗滑桩加固边坡的极限分析上限解

杨德升

(中土集团福州勘察设计研究院有限公司,福建 福州,350013)

孔隙水压力作用下抗滑桩加固边坡的极限分析上限解

杨德升

(中土集团福州勘察设计研究院有限公司,福建 福州,350013)

用对数螺旋线形的破坏机制和极限分析上限法,对抗滑桩加固边坡的稳定性进行了研究。基于构建的抗滑桩加固边坡的破坏机制,推导了抗滑桩加固边坡的内、外功率表达式。通过切线法将土体的非线性破坏准则引入到极限分析方法中,并结合强度折减法建立了抗滑桩加固边坡的安全系数隐式表达式。用最优化方法,计算得到了孔隙水压力作用下的边坡安全系数。在此基础上,分析了抗滑桩加固位置、孔隙水压力以及非线性抗剪强度等参数对抗滑桩加固边坡安全系数的影响。结果表明:土体抗剪强度对抗滑桩最佳布设位置的影响较小;非线性条件下,边坡安全系数随着初始黏聚力的增大而增大,随着抗拉强度和非线性系数的增大而减小。

边坡;抗滑桩;孔隙水压力;非线性破坏准则;上限解

在各类边坡工程加固手段中,抗滑桩因其布置灵活、填挖方量小和适用性强等优点,一直被广泛应用于各类土质边坡工程加固中[1-3]。抗滑桩在被广泛应用于工程中的同时,其加固机理及加固效果评价也得到了广泛研究。Ito等[4]基于塑性理论对边坡抗滑桩横向力的分布规律和作用机理的衡量方法进行了研究,并建立了抗滑力与抗剪强度之间的关系式;Li等[5-6]分析了地震荷载对边坡抗滑桩加固效应的影响;Nian等[7]研究了非均质和各向异性土边坡的抗滑桩加固效果;Gao等[8]借助极限分析方法,对边坡三维状态下的抗滑桩加固效果进行了分析。

目前,对于边坡抗滑桩的研究多着重于其加固机理,而对于复杂条件下抗滑桩加固边坡的稳定性计算方面尚存在不足。因此,本文借助极限分析上限原理,针对土体强度的非线性特征和孔隙水压力的不利影响,对抗滑桩加固边坡安全系数的计算方法进行研究,并获得相关参数的影响规律,以期对工程的设计和施工提供有益的指导。

1 极限分析上限法与非线性破坏准则

1.1 极限分析上限法

极限分析上限法可有效确定为保持某一工程结构稳定所需的荷载及其极限临界状态,因而得到越来越多的重视。在边坡工程中,上限法应用的首要条件在于确立边坡的破坏机制和相容速度场。在相容的速度场内,当外力功率大于内能耗散功率时,土工结构处于破坏状态,两者相等时,视为极限状态。极限分析上限法即是寻找最为危险的破坏状态,从而得到边坡的稳定性系数。在构建破坏机制的基础上,分别通过计算各项外力和内能量耗散功率,可以获得边坡稳定的极限状态能量平衡方程,即Wext=Dint。其中,Wext和Dint分别为临界破坏机构对应的总外力功率和内能耗散功率。

1.2 非线性Mohr-Coulomb破坏准则

对于符合Mohr-Coulomb破坏准则的土体,其强度用黏聚力c和内摩擦角φ来表征。然而,大量的试验证明,土体强度参数并不是常量,而是随着土体单元应力的变化而变化的[9-10]。土体的抗剪强度包络线实际是如图1所示的曲线。该强度包络线可由幂指数形式的表达式τ=c0(1+σn/σt)1/m进行描述[11]。式中c0为初始黏聚力,即正应力为0时的土体黏聚力,σt为轴向抗拉强度的绝对值,σn和τ分别为剪切面上的正应力和剪切应力。该表达式适用于黏性土。将该方程绘制成曲线如图1所示,曲线恒定通过(σt,0)和(0,c0)两点,m决定了曲线的弯曲程度。

由于非线性破坏准则的强度包络线为一条曲线,描述土体强度的c(纵轴截距)和φ(斜率)值与土体应力状态有关。鉴于此,杨小礼等[12]提出了“切线法”,即过强度包络线上任意一点作包络线的切线,并以此切线的纵轴截距ct和斜率ϕt表示土体强度的方法。该切线方程为τ=ct+σntanϕt。其中,ct和tanϕt分别为切线的纵轴截距与斜率,即等效的黏聚力和内摩擦角,且

在采用切线法进行优化分析时,ϕt将被视为一个自变量带入到各式中。以切线强度代替非线性强度,简化了非线性破坏准则的应用困难,文献[9-10]证明了其有效性。

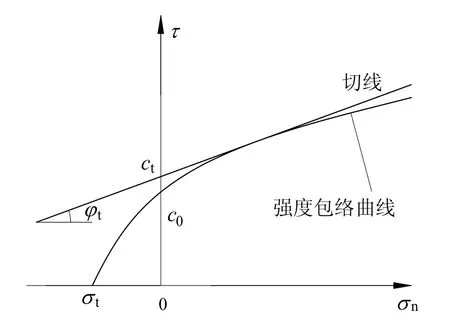
图1 非线性Mohr-Coulomb破坏准则及其切线

2 抗滑桩加固边坡破坏机制及能耗计算

2.1 抗滑桩加固的边坡破坏机制

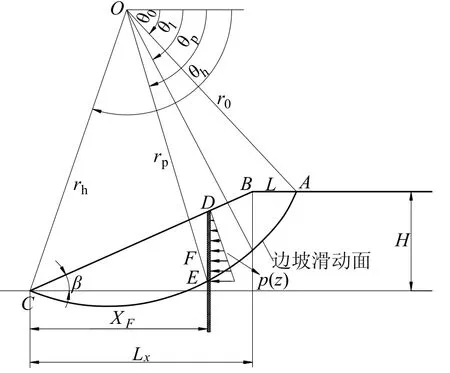
图2 抗滑桩加固边坡破坏机制

边坡稳定性计算一般认为是二维平面应变问题。构建的抗滑桩加固边坡的旋转破坏机制如图2所示,边坡高度和坡角分别为H和β,滑移体视为刚性体,沿滑移面AC绕中心O点产生滑动。r0和rh分别为初始和最终的旋转半径,ω为旋转速度。曲线AC为对数螺旋线,其极坐标表达式为r=r0e(θ−θ0)tanϕt,其中,ϕt为等效内摩擦角。图2中,Lx=H/tanβ为边坡水平方向长度;DE为边坡抗滑桩,XF=nLx(0≤n≤1.0)为抗滑桩布设位置,p(z)为抗滑桩提供的阻滑力,θp和rp分别为描述桩与滑移面交点位置的旋转角度和旋转半径。

2.2 抗滑桩加固边坡的能耗计算

图2所示的破坏机制中,外力功率由滑动块体的重力和孔隙水压力提供,内能耗散功率则发生在边坡滑移面上。抗滑桩的阻滑作用简化为沿深度分布的抗滑力所引起,相应地对破坏机构做功。

(1)土体重力功率。根据破坏机制的几何关系,边坡滑动土体重力功率可以表示为其中,

(2)孔隙水压力功率。工程实际中,孔隙水压力的分布较为复杂。文献[13]引入孔隙水压力系数ru,认为边坡水头与土体重力的分布类似,孔隙水压力u=ruγh。ru根据边坡坡体内的水力梯度近似得到,当只考虑静水压时,ru=γw/γ,其中,γw为水容重,γ为土体自然状态下的容重。将孔隙水压力视为外力,对边坡滑移体产生影响。对于本文中的破坏机制,孔隙水压力功率可以表示为其中,A=积分界限通过等式确定。

(3)滑动面上的内能耗散功率。发生在滑动面AC上的内能耗散功率为通过速度间断面上任意一点的线速度矢量与该点对应的黏聚力的乘积,即

(4)抗滑桩提供的内能耗散功率。文献[4]基于塑性力学理论,认为抗滑桩的抗滑力与土体的抗剪强度有关,且沿深度呈线性分布。抗滑桩提供的力p(z)表示为其中c0为土体黏聚力,γ为土体重度,D1和D2分别为桩形心之间的距离和净距,D1−D2为桩的直径,z为桩距离边坡坡面的竖直距离,在计算抗滑桩提供的内能耗散功率时,将任意深度对应的抗滑桩抗力p(z)与该点处的矢量速度的乘积沿着边坡表面到滑动面的抗滑桩深度积分,即Dp=Fpsinθprpω,其中,Fp根据p(z)沿深度z的积分得到。

2.3 抗滑桩加固边坡能量平衡上限解

根据极限分析上限法,抗滑桩加固边坡的能量平衡方程为

强度折减法是将土体强度参数c和φ按相同系数进行折减,使边坡在折减后的土体强度参数下达到极限状态。这一方法对应的折减系数就是边坡安全系数其中,c′和ϕ′为边坡处在临界稳定状态时的土体强度参数。将其代入式(1),即可得到边坡安全系数隐式表达式Fs=minf(Fs,θ0,θh|ct,φt,γ,H,β)。

安全系数的求解可转化为最优化问题,即寻找最小的安全系数Fs,使其满足平衡方程。本文采用Matlab最优化工具箱中的序列二次优化法进行求解,满足的约束条件为

3 抗滑桩加固边坡效应的非线性上限解参数分析

用前面获得的孔隙水作用下抗滑桩加固边坡的能量极限平衡状态方程,对各参数条件下抗滑桩加固边坡的安全系数进行计算求解。分析内容包括线性条件下的抗滑桩布设位置、非线性条件下的抗滑桩布设位置、边坡坡角、土体强度参数及孔隙水压力系数等因素对边坡稳定性的影响。

3.1 线性条件下抗滑桩最佳加固位置分析

当采用线性破坏准则描述土体抗剪强度时,土体强度参数c、ϕ为固定值。图3(a)和(b)分别为线性条件下不同黏聚力和内摩擦角条件下边坡安全系数随抗滑桩布设位置改变而变化的曲线图。参数选取为:边坡高度H=13.7 m,边坡坡角β=30°,D1=1.5 m,D2=0.9 m。此外,图3(a)中内摩擦角φ=30°,黏聚力c分别为10、15、20、25和30 kPa;图3(b)中土体黏聚力c=15 kPa,内摩擦角φ分别为10°、15°、20°、25°和30°。

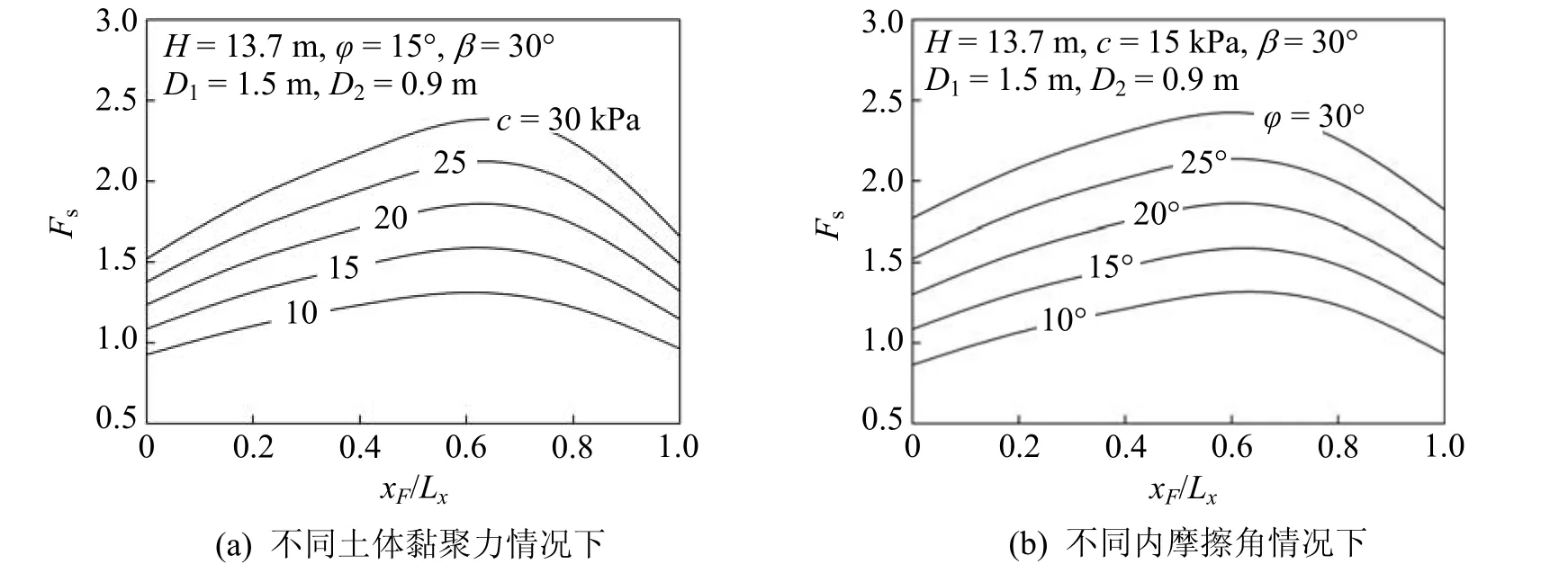
图3 土体强度参数对抗滑桩加固边坡的参数分析

从图3可见,边坡的安全系数随黏聚力c和内摩擦角φ的增大而线性增加。当抗滑桩布设于坡顶到边坡中间位置之间,即xF/Lx≈ 0.7时边坡安全系数最大,加固最为有效。同时,边坡土体强度参数对抗滑桩的最佳加固位置几乎无影响,即抗滑桩的最佳加固位置几乎不因强度参数的变化而改变。

3.2 非线性破坏准则下抗滑桩加固边坡最佳加固位置分析

图 4(a)为不同非线性系数条件下边坡安全系数随抗滑桩布设位置改变而变化的参数分析结果;图4(b)为不同抗滑桩布设位置条件下安全系数随非线性系数增大而变化的参数分析结果。参数选取为:边坡高度H=13.7 m,边坡坡角β=30°,土体初始黏聚力c0=20 kPa,σT=30 kPa,D1=1.5 m,D2=0.9 m。此外,图4(a)中非线性系数分别为m=1.2、1.4、1.8、2.0、2.5;图4(b)中抗滑桩布设位置分别为xF/Lx=0、0.2、0.4、0.6。

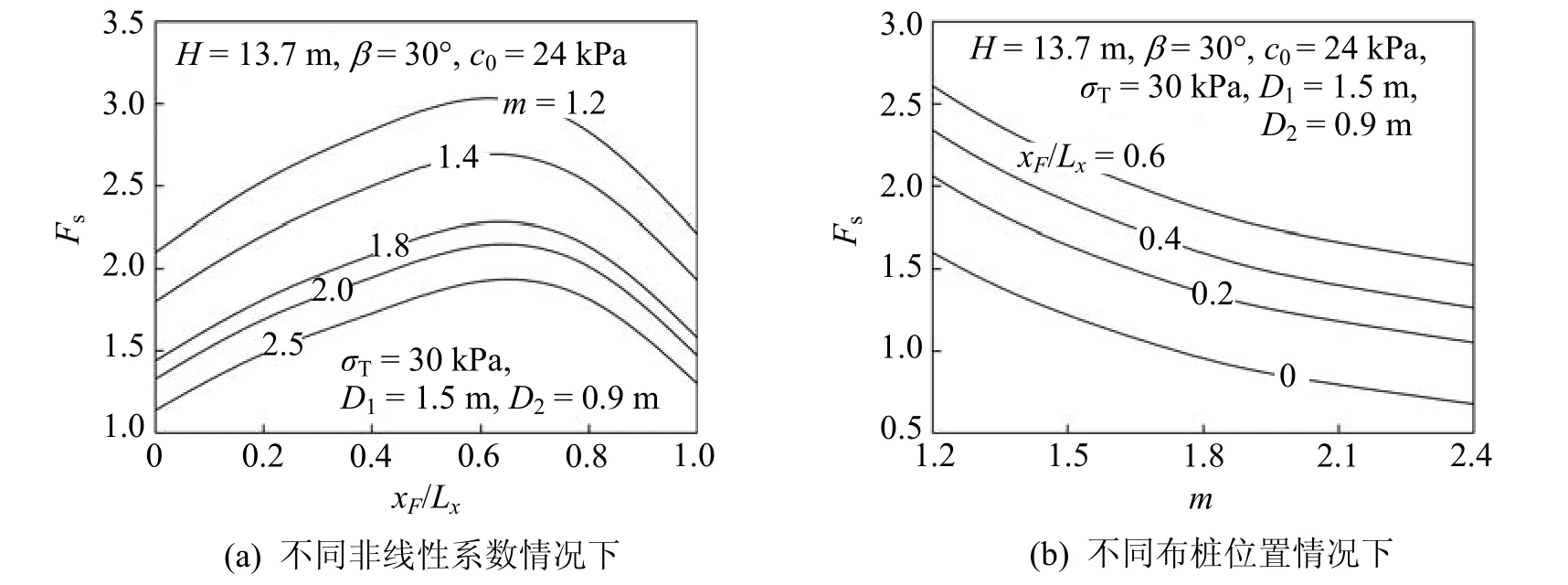
图4 非线性强度参数对抗滑桩加固边坡的参数分析

从图 4(a)可知,在同一位置布设抗滑桩时,边坡的安全系数随着非线性系数的增大而不断减小,但是非线性系数对最佳布桩位置亦无明显影响;在边坡几何条件一致的情况下,非线性破坏准则与线性准则的抗滑桩最佳加固位置几乎是一致的;从图4(b)中可以看出,随着非线性系数的增大,边坡安全系数不断减小,同时变化速率亦逐渐减小,即逐渐趋于平稳。

3.3 孔隙水作用下抗滑桩加固边坡的稳定性分析

图 5(a)～(c)分别为不同黏聚力、抗拉强度和非线性系数条件下边坡安全系数随孔隙水压力系数改变而变化的参数分析结果;图 5(d)为不同孔隙水压力系数条件下边坡安全系数随边坡坡脚改变而变化的参数分析结果。参数选取为边坡高度H=13.7 m,土体黏聚力D1=1.5 m,D2=0.9 m,其余参数如图5所示。

图5 孔隙水压力作用下抗滑桩加固边坡的安全系数

从图 5(a)～(c)可知,边坡安全系数随着初始黏聚力的增大而增大,随着抗拉强度和非线性系数的增大而减小,并趋于平缓。安全系数随着孔隙水压力作用的加强而减小。不同的初始黏聚力和抗拉强度条件下,改变孔隙水压力大小对稳定性的影响有所变化。而在不同非线性系数条件下,在ru从0增大到0.2的过程中,每增加0.05,边坡安全系数减小的量值均近似相同,即呈现一个近似的线性变化。图5(d)显示了不同边坡坡角情况下,安全系数随孔隙水系数ru增大而变化的规律,一个较为明显的规律是,安全系数在边坡坡角β较小时变化更为剧烈,随着β的不断增大,其变化趋于缓和。

4 结论

基于极限分析上限原理与非线性强度破坏准则,本文研究了孔隙水作用下的抗滑桩加固边坡安全系数的计算方法。通过参数分析,分别对抗滑桩布置位置、抗剪强度参数以及孔隙水压力系数等多因素对抗滑桩加固效果的影响进行了分析,并获得以下主要结论。

(1)边坡抗滑桩对边坡安全系数的提高作用明显。土体抗剪强度的增加将使边坡安全系数增大,但强度参数对抗滑桩最佳布设位置的影响较小;在边坡几何条件一致的情况下,非线性破坏准则与线性准则的抗滑桩最佳加固位置几乎是一致的。

(2)边坡安全系数随着初始黏聚力的增大而增大,随着抗拉强度和非线性系数的增大而减小。不同的初始黏聚力和抗拉强度条件下,孔隙水压力的变化对稳定性的影响程度有所变化。而在不同非线性系数条件下,随着孔隙水压力的增大,边坡安全系数减小的量值均近似相同。

[1]罗根传,何忠明,曾铃.高速公路改扩建工程边坡抗滑桩加固效果数值分析[J].中南大学学报(自然科学版),2015,46(6):2 244-2 249.

[2]王聪聪,李江腾,廖峻,等.抗滑桩加固边坡稳定性分析及其优化[J].中南大学学报(自然科学版),2015,46(1):231-237.

[3]颜可珍.基于Fisher判别分析法岩质边坡稳定性评价[J].公路,2010(1):1-4.

[4]Ito,T,Matsui.Design method for stabilizing piles against landslide-one row of piles [J].Soil and Foundations,1981,21(1):21-37.

[5]Li X P,He S M,Wang C H.Stability analysis of slopes reinforced with piles using limit analysis method [J].Geotechnical Special Publication,2006,9:105-112.

[6]Li X P,He S M,Wu Y.Seismic displacement of slopes reinforced with piles [J].Journal of Geotechnical &Geoenvironmental Engineering,2010,136(6):880-884.

[7]Nian T K,Chen G Q,Luan M T,et al.Limit analysis of the stability of slopes reinforced with piles against landslide in nonhomogeneous and anisotropic soils [J].Canadian Geotechnical Journal,2008,45(8):1 092-1 103.

[8]Gao Y F,Ye Mao,Zhang F.Three-dimensional analysis of slopes reinforced with piles [J].Journal of Central South University,2015,22(6):2 322-2 327.

[9]张迎宾,李亮,赵炼恒,等.基于非线性破坏准则的边坡稳定性极限分析[J].岩土力学,2011,32(11):3 312-3 318.

[10]王洪涛,李术才,王琦,等.非线性破坏准则下水平浅埋条形锚板抗拔承载力的极限分析[J].工程力学,2014,31(2):131-138.

[11]Baker R.Nonlinear Mohr Envelopes based on triaxial data [J].Journal of Geotechnical and Geoenvironmental Engineering,2004,130(5):498-506.

[12]杨小礼,李亮,刘宝琛.非线性破坏准则对竖直边坡稳定性分析的影响[J].岩石力学与工程学报,2004,23(4):592-596.

[13]Michalowski R L,Nadukuru S S.Three-Dimensional limit analysis of slopes with pore pressure [J].Journal of Geotechnical and Geoenvironmental Engineering,2013,139(9):1 604-1 610.

(责任编校:江河)

Nonlinear upper bound analysis of slope stability reinforced by piles subjected to pore water pressure

Yang Desheng
(CCECC Fuzhou Survey and Design Insitute Co Ltd,Fuzhou 350013,China)

According to the logarithmic failure mechanism and the upper bound method of limit analysis,the stability of slope reinforced with piles is studied.Based on the failure mechanism of slope strengthened by piles,the internal and external power expressions are derived.The tangent method is also introduced to consider the non-linear criterion of soil,and then the implicit expression of safety factor is obtained.The safety factor of slope under pore water pressure is calculated by the optimization method.On the base of this,the effects of the reinforcement position of pile,pore water pressure and nonlinear shear strength parameters on safety factor are studied.The calculation results show that shear strength has less impact on optimum placement of anti-slide piles,and under nonlinear criterion,the safety factor increases with the increasing initial cohesion but decreases with the increasing tensile strength and nonlinear coefficient.

slopes;anti-sliding piles;pore water pressure;nonlinear failure criterion;upper bound solution

P 642.22

A

1672-6146(2017)02-0084-06

杨德升,yangdesheng@ccecc.com.cn。

2017-02-06

10.3969/j.issn.1672-6146.2017.02.020