一维定常对流扩散反应方程的高精度紧致差分格式

祁应楠, 武莉莉

(宁夏师范学院 数学与计算机科学学院， 宁夏 固原 756000 )

一维定常对流扩散反应方程的高精度紧致差分格式

祁应楠*, 武莉莉

(宁夏师范学院 数学与计算机科学学院， 宁夏 固原 756000 )

针对一维定常对流扩散反应方程，提出了一种四阶精度的有理型紧致差分格式，其局部截断误差为O(h4)；然后通过Richardson外推技术和算子插值法将本文格式的精度提高到六阶.因为格式仅涉及到3个网格基架点，所以对于Dirichlet边值问题，由差分格式可得三对角线性方程组，可采用追赶法进行求解.最后通过数值算例验证了本文方法的精确性和可靠性.

对流扩散反应方程； 高阶紧致格式；Richardson外推； 有限差分法

对流扩散反应问题是流体力学、传热学、传质学等学科以及环境、化工等应用领域中经常遇到的典型问题之一，由于问题的准确解往往很难获得，所以人们经常采用数值方法来寻求问题的近似解.目前，所流行的近似计算方法包括有限差分法、有限元法和边界元法等.其中有限差分方法是一种常用的数值计算方法.目前，国内外已经有许多有关该问题高阶紧致差分格式的研究报道.如：魏剑英[1]针对一维对流扩散方程，提出了一种指数型高阶紧致差分格式.王彩华[2]利用泰勒展开公式和数项级数收敛性给出了一线性对流扩散问题的一类高精度紧致差分格式.田芳和田振夫[3]基于非均匀网格上函数的泰勒级数展开，构造了非均匀网格上的高精度紧致差分格式.Sun和Zhang[4]构造了定常对流扩散反应方程的多项式型四阶紧致差分格式，并用Richardson外推法[5]和算子插值技术将格式的精度提高到了六阶.Tian和Dai[6]构造对流扩散问题的指数型格式，其空间具有四阶精度.文献[7]研究了非定常对流扩散方程的有理型高阶紧致差分格式并得到了很好的计算效果.杨志峰等[8]构造了含源项非定常对流扩散问题的紧致四阶格式.文献[9-11]研究了利用样条插值的方法来构造高精度紧致差分格式.

文献[12]通过消除对流项，并利用Pade格式，构造了一维非定常对流扩散反应方程无条件稳定的四阶紧致差分格式.文献[13]针对非定常对流扩散方程，对空间采用三点紧致差分格式，并对时间采用单对角隐式Runge-Kutta方法进行离散，得到了截断误差为O(τ4+h4)的无条件稳定的隐格式.文献[14]通过简单的分裂算法及增加特殊网格点的方法，对时间的处理采用C-N格式与向后欧拉结合的技巧，推导出求解高维非定常对流扩散反应方程的隐式差分格式.

本文针对一维定常对流扩散反应方程，基于截断误差余项修正思想，并结合原方程本身，推导得到了求解该方程的一种四阶精度的有理型紧致差分格式.然后采用Richardson外推法和算子插值技术将格式的精度提高到六阶.最后给出了数值算例.

1数值计算方法

本文讨论的方程模型为两点边值问题：

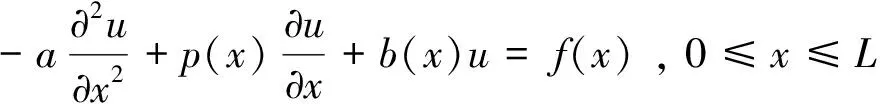
(1)

其中，边界条件为：u(0)=q0，u(L)=qL.这里，a，p(x)，b(x)分别为扩散、对流和反应项系数.且a>0，p(x)和b(x)均为关于空间变量x的光滑函数.

将式(1)改写为：

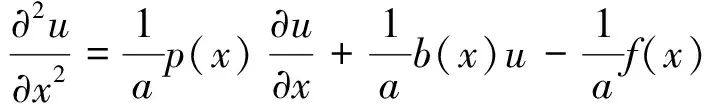
(2)

由此定义空间一阶和二阶导数的中心差分算子为：

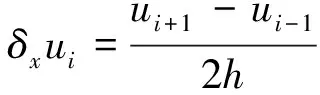
(3)

(4)

将式(1)利用中心差分代替，并利用关于u的一阶数和二阶导数的定义，可得：

(5)

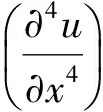
(6)

(7)

将式(6)代入式(7)消去xi化简可得：

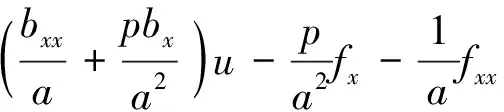
(8)

将式(6)和式(8)代入式(5)可得：

fi+O(h4).

(9)

将式(3)和式(4)代入式(9)，略去高阶项后化简整理可得：

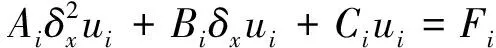
(10)

其中

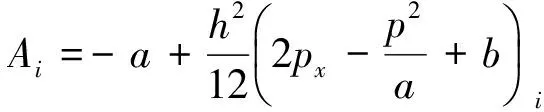
(11)

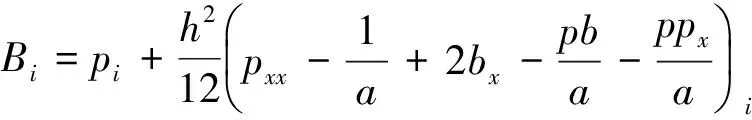
(12)

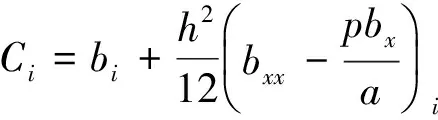
(13)

(14)

式(10)即为多项式型四阶紧致(FOC)差分格式，此格式色散误差和耗散误差较大.为了能精确数值求解此类方程，我们推导一种有理型的四阶紧致差分格式.

将式(2)代入式(6)可得：

(15)

(16)

将式(2)和式(15)代入式(7)，整理可得：

(17)

令

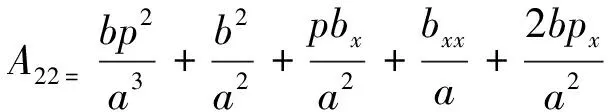
则式(17)可化简为：

(18)

将式(16)和式(18)代入式(5)，整理可得：

O(h4)，

(19)

(20)

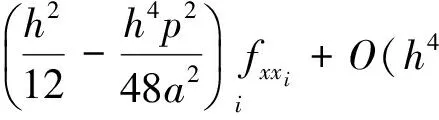
(21)

令

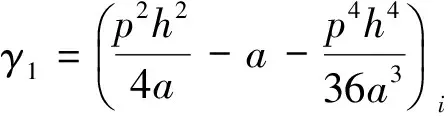
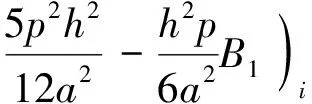
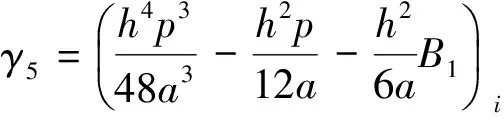
则式(21)可化简为：

(γ4f+γ5fx+γ6fxx)i+O(h4).

(22)

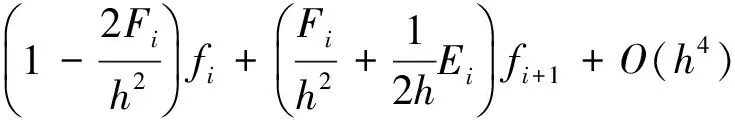
(23)

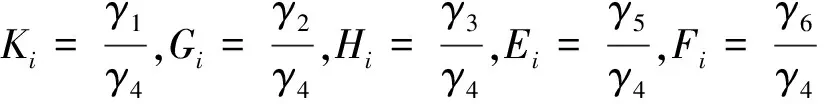
此格式的高阶截断误差为O(h4)，即此格式具有四阶精度.本文格式之所以称之为有理型格式，是因为其差分算子的系数为有理型函数，记为RHOC.

从推导过程可以看出，FOC格式只是其中的一种特殊情况，有理型格式的推导更具有广泛性.结合原方程可得到具有不同性质的高精度格式，对于不同性质的问题可选用与之相适应的格式进行求解，此类格式均为三个网格基架点，只发生系数的变化.

2Richardson外推

下面使用Richardson外推方法[5]将本文的四阶格式RHOC提高到六阶精度.

定义：

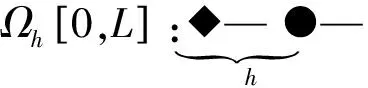
0 1 2 3 4……N-1N

(24)

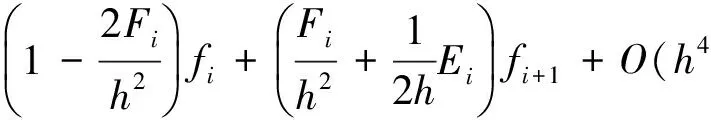
(25)

由于细网格上偶数点(菱形点)已经算出，因此只须采用式(26)计算奇数点(圆点)，即可得如下算子插值公式：

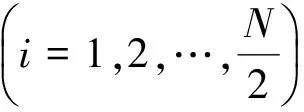
(26)

通过式(26)利用细网格上具有六阶精度的偶数点来计算奇数点，从而可使得细网格上点的精度均为六阶，整个过程我们将其记为RRHOC，其算法步骤如下：

3数值算例

为了验证本文格式的精确性和可靠性，分别采用RHOC格式和RRHOC格式对以下两个有精确解的问题进行数值实验，并与中心差分格式、多项式型四阶紧致格式(FOC)[4]和六阶格式(REC)[4]的计算结果进行比较.其中，L∞范数误差和收敛阶(Rate)的定义如下：

其中，Ui表示点xi处的精确解，ui表示点xi处的数值解，L∞(uh1)和L∞(uh2)分别表示网格步长为h1和h2时对应的L∞范数误差．

问题1：

该问题的精确解为：u(x)=ex.取：a=1，b(x)=x2+1，f(x)=x2ex.

问题2：

该问题的精确解为：u(x)=e-4πsin(x).取：a=1，p(x)=1，b(x)=1，f(x)=e-4π(cosx+2sinx).

表1 算例1当取不同h时，本文RHOC格式与中心差分格式和FOC格式[4]的最大绝对误差及收敛阶

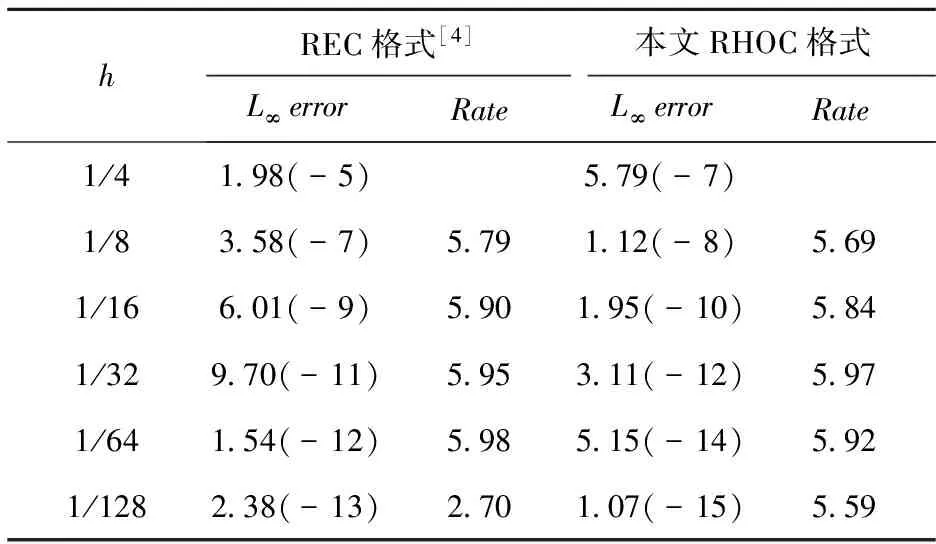
表2 算例1当取不同h时，本文RHOC格式和REC格式[4]的最大绝对误差及收敛阶

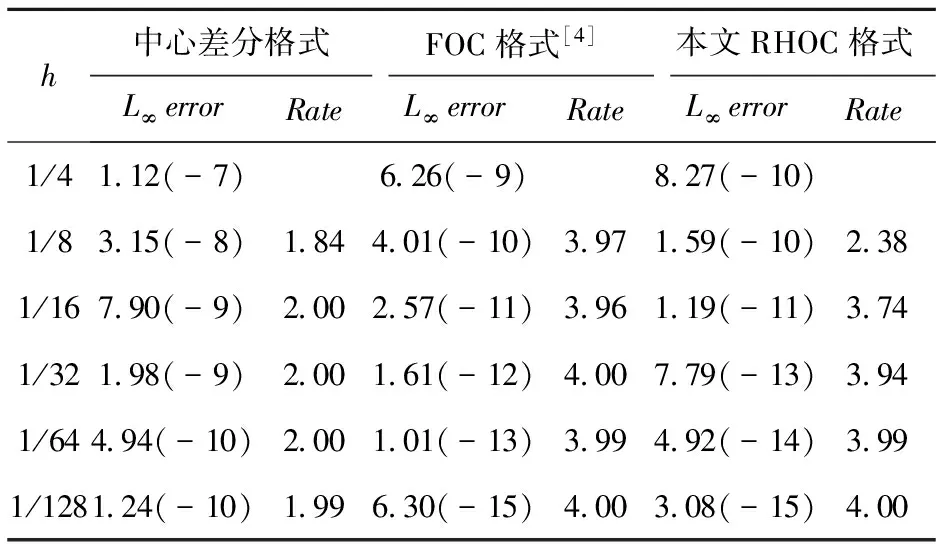
表3 算例2当取不同h时，本文RHOC格式与中心差分格式和FOC格式[4]的最大绝对误差及收敛阶

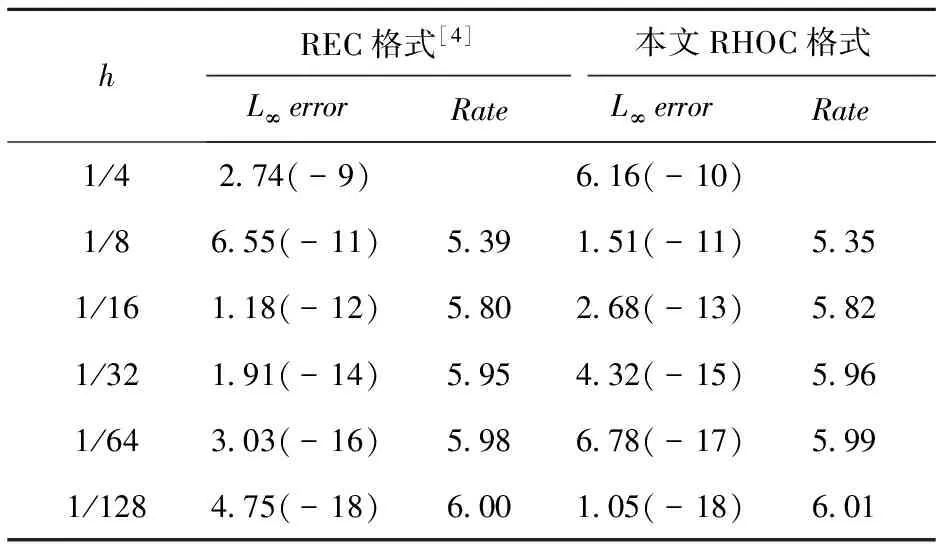
表4 算例2当取不同h时，本文RHOC格式和REC格式[4]的最大绝对误差及收敛阶

对于问题1和问题2，表1和表3列出了取不同步长h时，采用中心差分格式、FOC格式[4]与本文RHOC格式计算的L∞范数误差和Rate(收敛阶).不难得到，本文所提的四阶精度的有理型格式(RHOC)格式比多项式型格式(FOC) 和中心差分格式均具有更高的准确度.而且，当网格数不断增加时，RHOC格式的L∞范数误差比中心差分格式小四个数量级不等，比同是四阶的FOC格式计算结果更精确.表2和表4列出了取不同网格步长h时，REC格式[4]与本文RHOC格式的最大绝对误差和收敛阶，从表中可以看出经过外推和算子插值之后的REC格式和本文RHOC格式均有六阶精度，但是本文RHOC格式的计算误差明显优于REC格式[4].

4结论

本文基于中心差分格式的截断误差余项修正，并利用原方程本身，提出了数值求解一维两点边值问题的一种紧致的高精度差分方法，由理论推导可知所提格式为四阶精度.然后采用Richardson外推法和算子插值技术将格式的精度提高到六阶.最后，采用本文两种方法计算了两个数值算例，并与传统的中心差分格式以及文献[4]中的FOC格式和REC格式进行了对比，充分体现了本文方法的精确性和有效性.

[1] 魏剑英. 定常对流扩散反应方程的指数型高阶差分格式[J].宁夏大学学报(自然科学版)， 2012， 33(2):140-143．

[2] 王彩华. 一维对流扩散方程的一类新型高精度紧致差分格式[J].水动力学研究与进展， 2004， 19(5):655-663.

[3] 田 芳， 田振夫. 定常对流扩散反应方程非均匀网格上的高精度紧致差分格式[J].宁夏师范学院学报(自然科学版)， 2009， 26(2):219-225．

[4]SUNH，ZHANGJ.AHighorderfinitedifferencediscretizationstrategybasedonextrapolationforconvectiondiffusionequations[J].NumerMethodsPartialDifferentialEq， 2004， 20(1):18-32

[5]CHENEYW，KINCARDD.NumericalMathematicsandComputing[M]. 4thEd.CA：Brooks/ColePublishing，PacificGrove，CA. 1999．

[6]TIANZF，DAISQ.High-ordercompactexponentialfinitedifferencemethodsforconvection-diffusiontypeproblems[J].JComputPhys， 2007， 220:952-974．

[7] 赵 飞， 蔡志权， 葛永斌. 一维非定常对流扩散方程的有理型高阶紧致差分格式[J].江西师范大学学报(自然科学版)， 2014， 38(4):413-418．

[8] 杨志峰， 陈国谦. 含源项非定常对流扩散问题紧致四阶差分格式[J].科学通报， 1993， 38(2):113-116．

[9]LANGFG，XUXP.QuinticB-splinecollocationmethodforsecondordermixedboundaryvalueproblem[J].ComputerPhysicsCommunications. 2012， 183:913-921．

[10]GOHJ，MAJIDAA,ISMAILAIM.AquarticB-splineforsecond-ordersingularboundaryvalueproblems[J].ComputersandMathematicswithApplications. 2012， 64:115-120．

[11] 林建国，许维德，陶尧森.含源项非定常非线性对流扩散方程的三次样条四阶差分格式[J].水动力学研究与进展(A辑)， 1994， 9(2):599-602．

[12] 杨录峰，李春光.一种求解对流扩散反应方程的高阶紧致差分格式[J]. 宁夏大学学报(自然科学版)， 2013， 34(2): 101-104．

[13]PIAOX，CHOIHJ，KIMSD，etal.AfastsinglydiagonallyimplicitRunge-Kuttamethodforsolving1Dunsteadyconvection-diffusionequations[J].NumercalMethodsforPartialDifferentialEquations，2013(30):788-812．

[14]ADEMK.Finitedifferenceapproximationsofmultidimensionalunsteadyconvection-diffusion-reactionequations[J].JournalofComputationalPhysics， 2015， 285:331-349．

A high-order compact difference scheme forthe 1D steady convection-diffusion-reaction equation

QI Yingnan， WU Lili

(School of Mathematics and Computer Science, Ningxia Normal University, Guyuan, Ningxia 756000)

In this paper, a rational high-order compact difference scheme for solving the 1D steady convection-reaction-diffusion equation is proposed. The local truncation error of the scheme isO(h4). And then the Richardson extrapolation and operator interpolation techniques are employed to obtain a sixth order accuracy solution. Because only three basic grid points are used in the scheme, the linear system arising from the scheme for Dirichlet boundary problem is tridiagonal. It’s able to be solved by the forward elimination and backward substitution algorithm. Finally, numerical experiments are carried out to demonstrate the accuracy and the effectiveness of the present method.

convection-reaction-diffusion equation; high-order compact scheme; Richardson extrapolation; finite difference method

2016-09-18.

宁夏高等学校科学研究项目(NGY2015115)；宁夏自然科学基金项目(NZ15259、NZ16251)；宁夏师范学院项目(NXSFZD1707，NXSFZD1709，NXSFZD1710).

1000-1190(2017)01-0001-06

O241.8

A

*E-mail: gysz9695@163.com.