基于改进ICA算法对云南地区重力固体潮中地震前兆信息的提取与识别
张艾怡, 全海燕*, 矣昕宝
(1.昆明理工大学 信息工程与自动化学院, 昆明 650500; 2.西双版纳职业技术学院, 云南 西双版纳 666100)
基于改进ICA算法对云南地区重力固体潮中地震前兆信息的提取与识别
张艾怡1, 全海燕1*, 矣昕宝2
(1.昆明理工大学 信息工程与自动化学院, 昆明 650500; 2.西双版纳职业技术学院, 云南 西双版纳 666100)
固体潮信号是地球自转在月球和太阳作用下产生的混合复杂信号,其中包含大量的谐波分量,而实际重力固体潮信号中包含了丰富的地震前兆信息.该文提出一个重力固体潮信号的正交分解模型,通过将重力固体潮信号谐波分量,分解在两个正交的方向上,以提取独立的谐波分量:半日波信号、日波信号、长周期波信号.在重力固体潮地震前兆信息分析中引入ICA算法,结合ICA的自身的特点进行算法优化,对重力固体潮信号中包含的三类谐波进行提取.通过对重力固体潮信号中包含的长周期波的分析,研究长周期波的时序变化特征,从中读取其包含的震颤异常波从而提取地震前兆信息.通过对云南地区的实际震例分析表明,长周期波在地震前后的确存在异常变化特征量,此类异常变化常出现在地震前和地震后大约30 d左右.得到的时序特征量的变化容易观察,对于地震前兆信息的分析具有明确的物理意义.
地震前兆信息; 重力固体潮; 长周期波; ICA
固体潮是在日、月(非常微小的部分来自于离地球较劲的行星)引潮力的作用下,固体地球产生的周期性形变的形象[1].固体潮是唯一能够预先计算出的地球物理现象,已经有学者对固体潮理论值推算出了公式[2-3].引潮力是作用在地球的单位质点上的日、月引力和地球绕地月(和地日)公共质心旋转所产生的惯性离心力的合力.随着作用点的位置不同和日、月相对于地球的位置变化,引潮力的大小、方向也发生改变.作为地球上最大的周期性应变的固体潮汐,峰-峰变化幅值度科大5×10-8,是触发地震的一个极可能的因素[4].同时,很多学者通过计算和分析加强了此种结论,指出潮汐最大剪应力与强震的发震时刻有一定的相关性[5].同时,太阳和月球对地球的固体潮力远远小于地壳岩石强度,单一的固体潮力不能使岩石破裂而引发地震;太阳和月球的加卸载作用主要集中于低纬度地区,与地球地震带范围基本吻合[6].因此研究固体潮中包含的地震前兆信息,对于地震的预测和预防具有很大的物理意义.
通过对固体潮信号的分析,可知固体潮信号是一种复杂的混合信号,其中包含很多的谐波分量,按照周期的长短可以分为日波、半日波和长周期波.在研究固体潮信号的过程中,主要是从这些谐波分量中分析地球物理信息,用于观测和对比.在固体潮观测中,强震前固体潮的实际观测值会出现震颤异常波[7],此类可归纳为地震的前兆信息.本文从固体潮谐波分量的产生机制上分析了固体潮正交分解模型,将提取的各谐波分量能够与模型中所提出的方向一一对应,从而更够更好的分析固体潮信号中包含的地震前兆信息.
ICA(Independent Component Analysis, 独立成分分析)是一种重要的盲源分解方法,其目的是从多通道测量所得到的由若干独立信源线性组合成的观测信号中,将其中的独立成分分离开[8].地球上任意一点受到的重力固体潮引潮力主要是由月亮、太阳及地球自转各自独立产生而影响的.本文利用PBIL算法的学习机制对ICA算法进行改进.本文用改进的ICA算法对固体潮信号进行分析,研究了长周期波的波动异常,捕捉到了地震前后的变化信息,应用理论值和观测值的对比对此进行了验证.结果表明,得到的长周期波的异常波动可以判断为地震的异常信息.
1固体潮正交分解模型
固体潮正交分解模型,是依据力学分析中常用的正交分解推出的,其模型如图1所示.
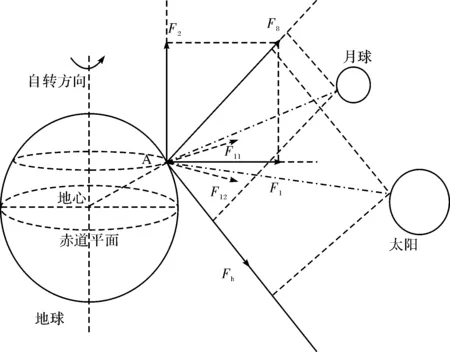
图1 固体潮正交模型原理图Fig.1 The orthogonal decomposition model of gravity earth tide
重力固体潮的理论值已经有学者进行不断地完善和精进[10],而重力固体潮的实际观测值已经可以通过一些仪器进行观测,目前我国使用的潮汐重力仪有6类[11].
2地震前兆信息量特征量
用于描述地震异常的综合特征量应该具备以下特征:
1) 适用于对各种物理量纲的地震时序观测数据进行处理;
2) 异常的变化量越大, 综合特征量越大;
3) 大量震例表明, 相当数量的地震发生在异常结束之后, 说明在异常结束后的一时间内, 仍存在地震前兆信息[12].
3改进的ICA算法对重力固体潮进行分析
ICA是一种热门的盲源分离算法,算法通过得到源信号的非高斯性高阶统计量[13],进而得到源信号的近似估计.ICA算法的实质是通过选择合适的目标函数和优化算法,对ICA算法中的解混矩阵进行优化求解.本文利用负熵作为目标函数,同时采用PBIL算法对解混矩阵的求解进行优化.
PBIL算法是新兴的随机优化方法,与一般的进化计算方法不同,它是利用个体自身进行优化,依赖于一个独特的概率向量模型来指导整个搜索过程[14].在算法中,概率向量更新模型公式如下所示:
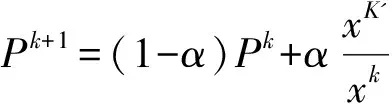
(1)
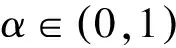
本文利用PBIL算法和ICA算法的结合来处理重力固体潮信号,对重力固体潮信号进行处理的基本步骤如下:
1) 获取观测点处的的重力固体潮信号.通过模型分析可知,重力固体潮信号的产生是由太阳、月球的引潮力以及地球的自转产生的,同时实际观测中会存在噪声信号,因此选取的重力固体潮信号应为4路信号,
G(t)=[G1(t),G2(t),G3(t),G4(t)].
3) 利用优化算法求解混矩阵
(1)初始化.包括粒子的数量M及粒子的维度D,并根据输入信号将其转化为4×4的M个解混矩阵W.设置最大迭代次数N,并开始循环i=1
(2)根据独立成分分析算法,得到
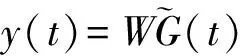
(2)
y(t)是源信号中的独立成分估计信号.
(3)利用负熵计算适应值.将负熵计算公式作为目标函数,负熵计算公式为:

(3)
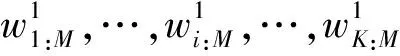
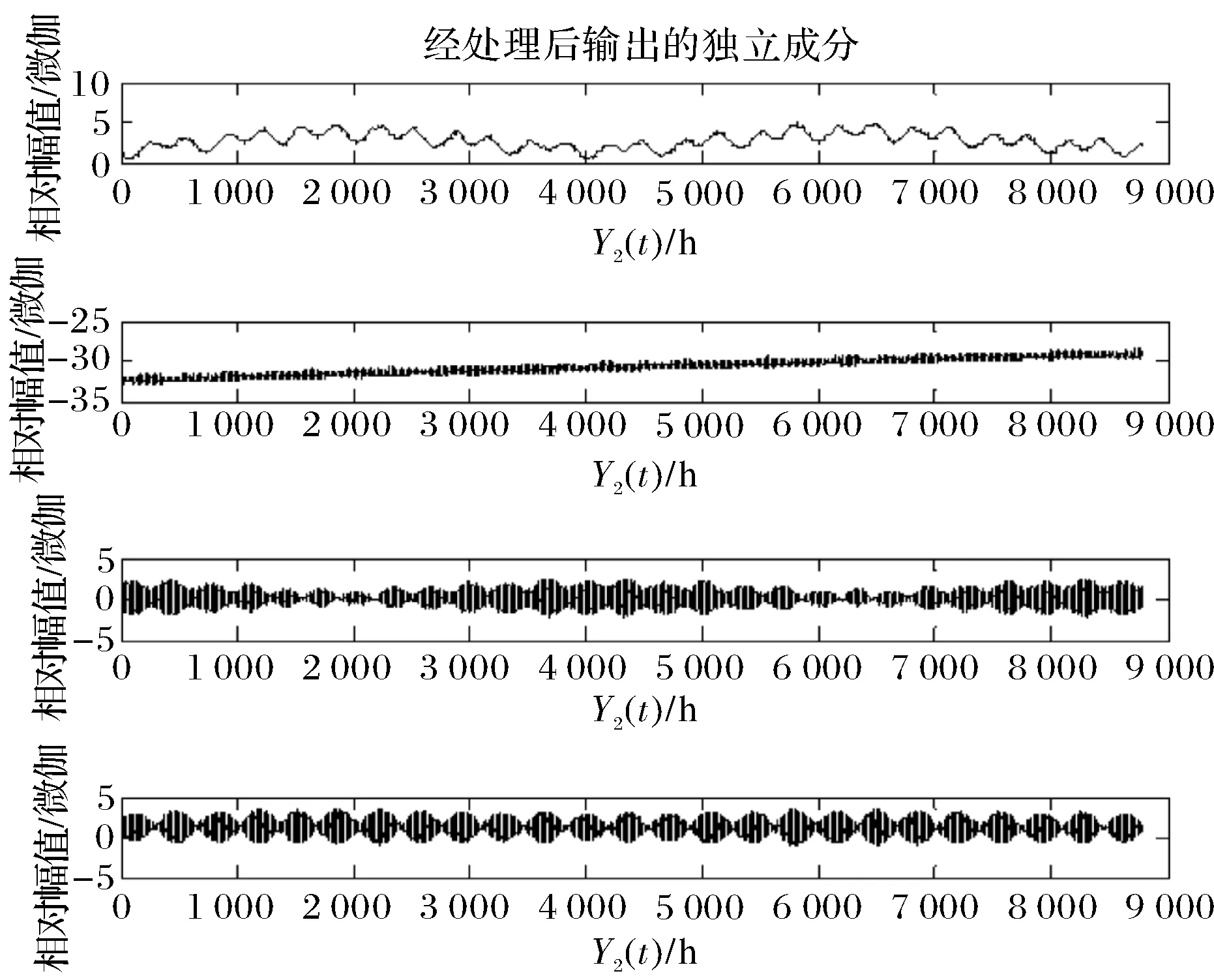
(5)当i 5) 从得到的长周期波中找出异常震动. 4.1地震震区分析 本文选取昆明地区近场地区,观测数据值来自黑龙潭昆明基准地震台(地理坐标25.1483;102.74694),地震记录只包括一下范围内的地震级别范围:4.5≤M≤5.5级地震(150 km以内)(震中距<1.35°),5.5 在信号的提取和分离过程中,要分离三类谐波信号和一类噪声信号,因此本文选取3路理论值信号和1路实测值信号.在实际观测信号中,固体潮信号受潮汐因子和零点漂移现象的影响较为严重,因此重力固体潮汐波的实测值比理论值要大[4].在此,本文将零点漂移也视为噪声信号.输入的待处理重力固体潮信号如图3所示. 图3 输入的重力固体潮信号Fig.3 The input gravity earth tide signal 经过改进ICA算法处理后的信号如图4所示,处理后的信号幅值单位成为相对幅值. 图4 利用模型分析和算法计算得到的谐波数据Fig.4 The output signal after processed 对分离后的重力固体潮信号,即图4中的信号进行谐量分析[4],忽略其他因素的影响,得到重力固体潮谐波分量信号的频谱图,如图5所示.再与杜森公式展开的理论值[16]进行对比,得到表1,如下所示,其中e代表10的幂次方. 通过对图4、图5和表1的分析可知:1)得到的处理后的重力固体潮信号的独立成分分别为重力固体潮信号中包含的三类独立谐波分量,分别为长周期波、日波和半日波,其分别对应正交分级模型中的F2长周期波方向、F11日波方向、F12和半日波方向,且相互独立;2)从图4和表1中可以清楚的看出日波和半日波之间存在一定的调制关系. 图5 输出的独立成分频谱分析图Fig.5 The frequencies of the output signals 根据重力固体潮信号经改进ICA算法处理后结果分析可知,Y1(t)为长周期波类.在进行地震实例分析和对比时,选取此路信号作为研究对象. 4.2地震实例分析 本文分析长周期波中的异常波动,来判断重力固体潮信号中的地震前兆信息.长周期波能够反映能量的强度积累过程,因此分析长周期波来提取地震前兆信息比较简便,也是目前较多数学者使用的 表1 信号频率值与理论频率值对应表 一种评测手段[17].根据图5对图4的分析计算可知,图4中,第3类信号为长周期波信号.本文经过了大量实验进行例证,但由于篇幅有限,在此我们仅分析了2000年的长周期波的异常波动,如图6所示,即固体潮信号中的震颤异常波分析,体现为平滑的曲线中出现了不规则形状的波形,通常具有突变性,呈现纺锤状[7]. 在信号分析的过程中,信号是按照每小时进行采点计算的,但是地震发生时间是按照天进行分析的,因此在本文后面的分析过程中,都进行了单位的相应换算. 图6 2000年重力固体潮长周期波中的异常点Fig.6 The abnormal point in long-period waves of 2000 inYunan 地震点及地震日期地震级别及距测试点离长周期波异常点时间差姚安(1月15日)65级,距6244km2月1日异常点出现在地震后的15d丘北(1月27日)55级,距14263km3月1日异常点出现在地震后的32d姚安(4月3日)45级,距17405km3月1日,5月2日异常点出现在震前的32天和震后的30d武定(8月21日)50级,距9167km8月3日,9月4日异常点出现在震前的19天和震后的15d 通过实验和震例分析,改进的算法不仅能够将重力固体潮信号中包含的三类谐波独立的分离开来,能够分别对日波、半日波和长周期波直接分析.地震是长时间的能量聚集爆发的结果,长周期波能够反映能量的聚集.通过对长周期波的分析,和大量的数据进行验证,在震前和震后一月左右会出现长周期波异常点[18],同时通过实际值和理论值的对比观测也映证了这个观点,表明长周期波的一些特征参数在地震前和地震后会出现明显的异常,符合本文提到的地震前兆信息量特征量具备的特征.本文对于地震前兆信息的研究具有非常清楚的物理意义.但本文仅选取了云南地区作为震例分析,且均为低于4.5级以上的地震进行分析,因此存在一定的局限性.因此下一步,扩大监测地震范围进行数据分析,对地震前兆信息的提取做出更为精确的判断. [1] 徐建桥, 周江存, 陈晓东等. 武汉台重力潮汐长期观测结果[J]. 地球物理学报, 2014, 57(10): 3092-3093. [2] 郗钦文, 侯天敏. 固体潮汐与引潮常数[J]. 中国地震, 1986, 2(2):30-41. [3] 苏 融, 李胜乐. 基于拉普拉斯级数展开法的固体潮波类理论值计算[J]. 大地测量与地球动力学, 2013, 33(5):106-109. [4] 冯 锐. 地倾斜与地震[M]. 北京:地震出版社,1978:218-281. [5] 高锡铭, 殷志山, 王威中, 等. 固体潮应力张量对地震的触发作用[J]. 地壳形变与地震, 1981, 1(1):4-16. [6] 李启成. 固体潮力触发地震的可能性[J]. 黑龙江科技学院学报, 2011, 21(5): 386-388. [7] 蒋 骏,张雁滨,林 钢, 等. 固体潮观测中的震颤异常波[J].地球物理学报, 2012, 55(2):462-471. [8] 李云飞, 全海燕, 肖春梅. 基于EMD的ICA语音增强[J]. 华中师范大学学报, 2015, 49(1): 42-46. [9] 李云飞. 基于改进的HHT方法提取重力固体潮信号的地球物理信息[D]. 昆明:昆明理工大学, 2014. [10] 董 良,彭芳萍,杨 涛, 等. 2015.利用新参数和软件改进重力固体潮计算程序[J]. 地球物理学进展, 30(1):421-424. [11] 宋臣田, 宋彦云, 唐九安, 等, 地震监测仪器大全[M]. 地震出版社, 2008: 152-158. [12] 张 立, 平建军, 苏有锦. 云南地区总和地震前兆信息量及其短期映震能力分析[J]. 地震研究, 2006, 29(4): 325-331. [13] 周书仁, 梁昔明, 杨秋芬. 基于PSO与ICA的表情特征提取[J]. 计算机应用, 2007, 27(11):2792-2803. [14]GAOXZh,WANGXLetal,AhybridPBIL-basedharmonysearchmethod[J].NeuralComputing&Applications, 2012, 21(5): 1071-1083. [15] 郭 敏, 郭 靖. 含噪ICA模型的一种时频算法[J]. 华中师范大学学报(自然科学版),2015, 49(4): 515-519. [16] 北京大学地球物理系,武汉测绘学院大地测量系. 重力与固体潮教程[M]. 北京:地震出版社, 1982. [17] 张淑亮, 范雪芳, 李冬梅, 等. 大震前井水位长周期波生成机理的实验证据[J]. 山西地震, 2005, 3(122): 6-10. [18] 周 挚, 山秀明, 张 立, 等. 基于HHT提取昆明、下关重力固体潮的地震前兆信息[J]. 地球物理学报, 2008, 51(3):836-844. The earthquake precursor information of gravitytide in Yunnan based on improved ICA ZHANG Aiyi1, QUAN Haiyan1, YI Xinbao2 (1.Faculty of Information Engineering and Automation, KunmingUniversity of Science and Technology, Kunming 650500;2.Xishuangbanna Vacational and Technical College, Xishuangbanna, Yunnan 666100) Gravity earth tide signal is a kind of complex mixed signal which is caused by effect of the Moon and the Sun on the Earth rotation. The observed gravity tide includes much earthquake precursor information. An orthogonal decomposition model of gravity earth tide is proposed to decompose the gravity earth tide into two orthogonal direction, in order to extract the independent harmonic components from the gravity earth tide. The independent harmonic component are long-period waves, diurnal wave, and semi diurnal wave. Independent Component Analysis (ICA) is introduced in analysis of earthquake precursor information in gravity tide, which is used to analysis the three kinds of harmonic component. According to analysis on the long-period wave, the instantaneous sequence variation characteristics is studied. The Yunnan earthquakes cases show that long-period wave exists abnormal variation, and the changes emerge 30 days before and after the earthquake. The change of the abnormal variation is easy to observe and analysis, which has clear physical meaning to the analysis of the earthquake. earthquake precursor information; gravity tide; long-period wave 2016-03-23. 国家自然科学基金项目(41364002); 云南省自然科学基金项目(2009ZC048M); 昆明理工大学校人才培养基金项目( KKZ3201103022). 1000-1190(2017)01-0035-05 P223 A *通讯联系人. E-mail: quanhaiyan@163.com.
4地震震例分析

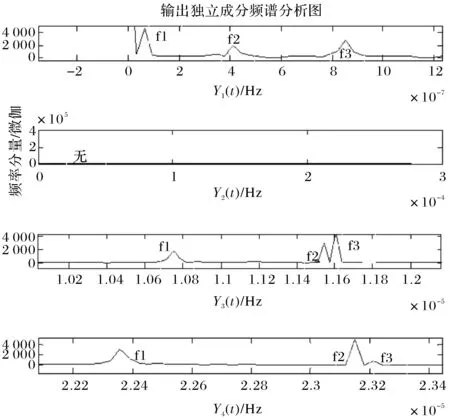
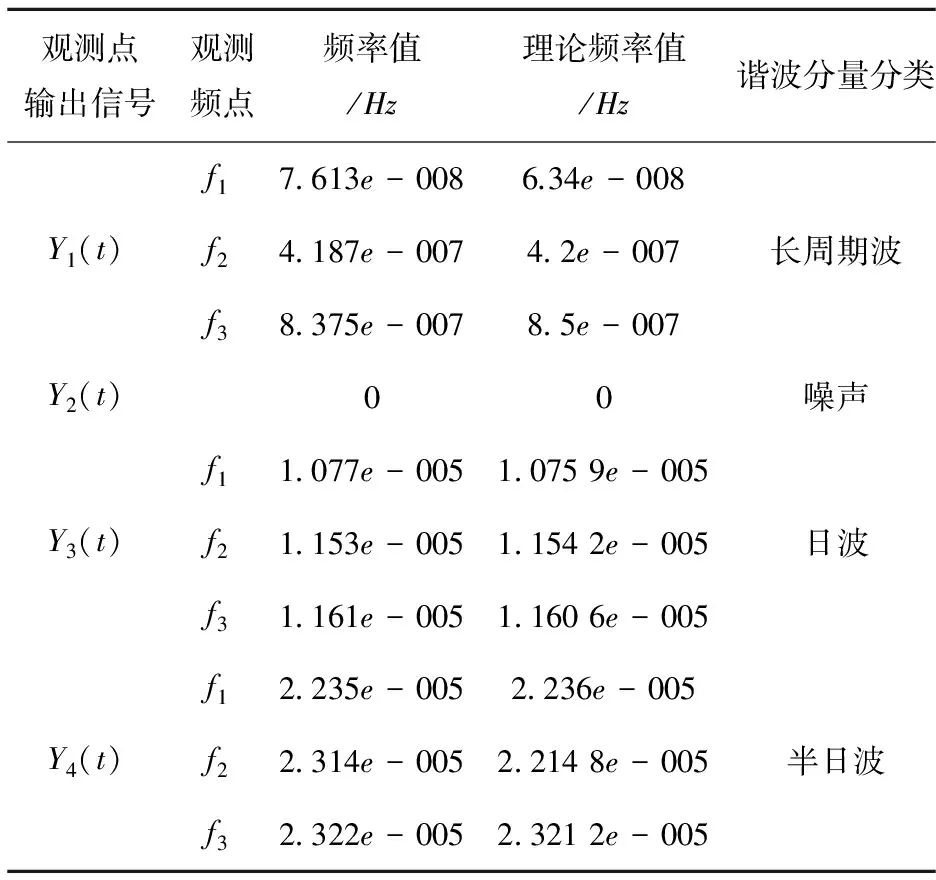
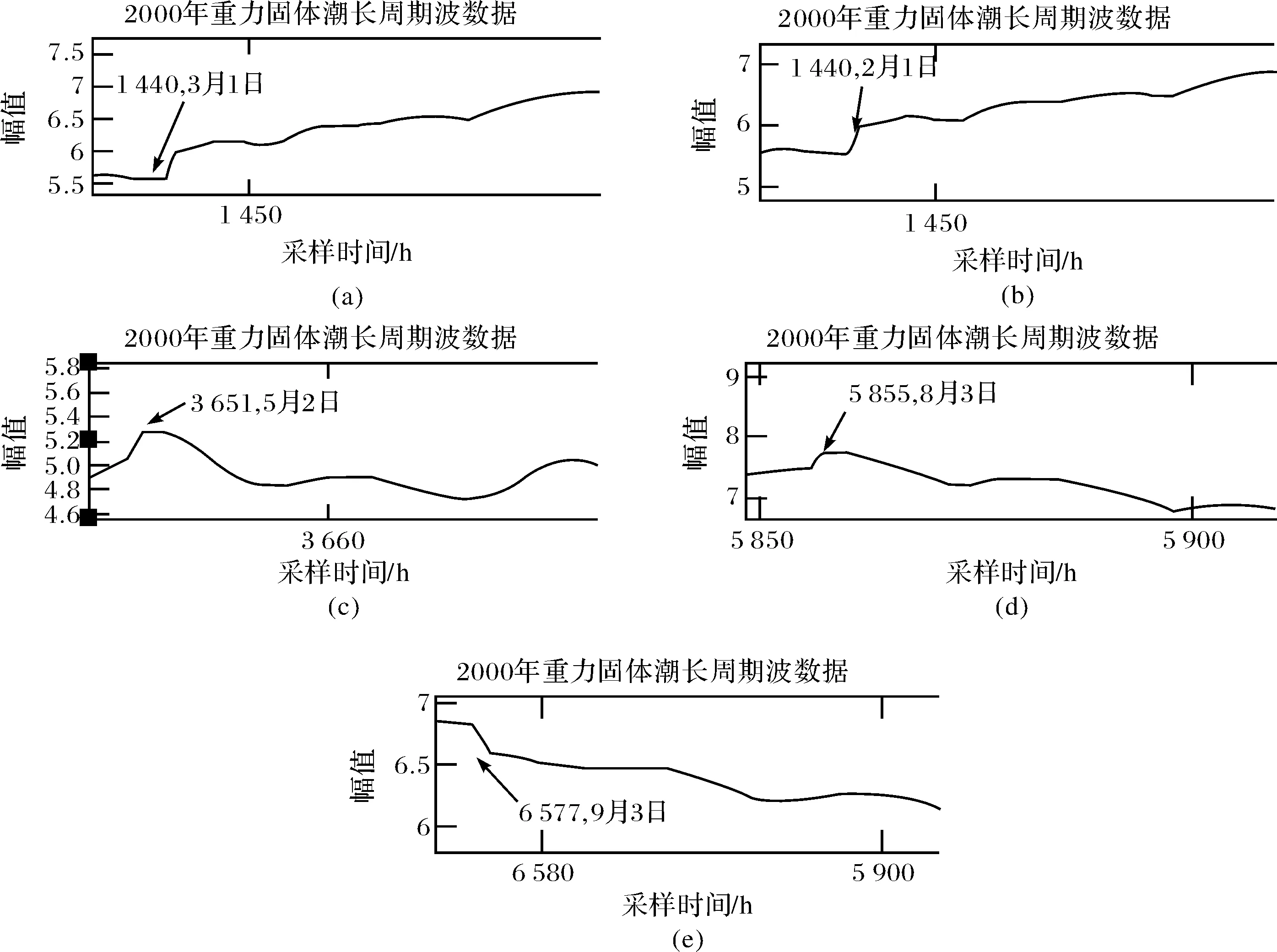

5总结

