如何在数学教学过程中培养学生的数学能力

北京市丰台区民大附中丰台实验学校 许士文

如何在数学教学过程中培养学生的数学能力

北京市丰台区民大附中丰台实验学校 许士文

数学是一门比较抽象又实践性强的学科，在数学教学过程中要培养学生的数学能力，发展学生的数学思维，全面提高数学质量，使人人学有价值的数学；人人都能获得必需的数学；不同的人在数学上有不同的发展。这是我们广大数学教育者的使命和职责。我在长期教学实践中总结了以下几点，与大家分享：

一、在教学中注重定理、性质、公式的探索发现过程，发展学生的合情推理和逻辑推理能力

对于定理、性质、公式、运算规律等知识的学习，应从学生已有的认知发展水平和已有的经验出发，遵循“由特殊到一般”的规律，结合具体的学习内容精心设计一系列问题，引导学生围绕这些问题进行实验、观察、分析、计算、推理、归纳、总结等数学活动，在活动中自主发现知识，从而得到相关结论，再引导学生证明猜想，从而得到数学定理、性质、公式。

例如在角平分线性质定理的教学中，我设计了以下问题引导学生进行试验探究：

（1）如图1，OA是∠BAC的平分线，点O是射线AM上的任意一点。

操作测量：取点O的三个不同的位置，分别过点O作OE⊥AB，OD ⊥AC,点D、E为垂足，测量OD、OE的长。将三次数据填入下表：

图1

（2）观察测量结果，猜想线段OD与OE的大小关系，写出结论：

（3）下面用我们学过的知识证明发现：

已知：如图1，AO平分∠BAC，OE⊥AB，OD⊥AC。

求证：OE=OD。（要求学生写出证明步骤）

显然，这个定理是同学们通过测量、观察、猜想、证明发现的，而且在探索的过程中，还受到了数形结合思想的熏陶，获得了数学活动经验，发展了学生的合情推理和初步演绎推理能力。

二、在教学中注重建立数学模型的过程，培养学生发现、提出、分析、解决问题的能力

所谓数学模型，是指针对或参照某种事物的特征或数量相依关系，采用形式化的数学语言，概括地或近似表述出来的一种数学结构。仔细研究课标（2011年版）规定的课程内容可以发现，其中绝大部分内容本身就是一个数学模型。从这个意义上来说，数学教学实际上就是教给学生前人构建的一个个数学模型，逐步形成数学模型思想的过程。因此，数学教学要结合具体的内容，充分体现“问题情境－建立模型－求解验证”的过程。

例如： A校和B校各有旧电脑12台和6台，现决定送给C校10台、D校8台，已知从A校调运一台电脑到C校、D校的运费分别是40元和80元，从B校调运一台电脑到C校、D校的运费分别是30元和50元，试求出总运费最低的调运方案及最低运费是多少。

这个问题就是考查学生通过建立数学函数模型解答实际问题的能力。为降低难度，我设计了下面两个小问题引导学生建立模型：

（2）我们试着用下面的图表示调运：

如果我们把总运费设为y元，根据上图，你能得出总运费y与x之间的关系式吗？它是一个一次函数吗？自变量x有什么样的范围？你能用函数性质解决本题吗？

学生在解答以上两个问题的基础上很容易建立模型：

解：设A校调运给C校x台电脑，那么A校调运给D校（12-x）台，B校调运给C校（10-x）台、D校（4+x）台。根据题意得：

自变量范围：4≤x≤10 ，∴当x=10时，y有最小值为860。

数学建模教学本身是一个不断探索、创新、完善和提高的过程，我们广大教师应不断研究新情况、新问题，在数学教学中努力帮助学生理解并掌握以下几种重要的数学模型：（1）方程（组）模型；（2）不等式（组）模型；（3）函数模型；（4）几何模型；（5）统计模型；（6）概率模型等。

三、在教学中注重数学综合实践活动，提高学生解决实际问题的能力

数学来源于生活，应用于生活，综合实践沟通了生活中的数学与课堂上的数学的联系，是帮助学生积累数学活动经验、培养应用意识与创新意识的重要途径，是学生综合运用所学知识和生活经验，独立思考或与他人合作，经历发现和提出问题，分析和解决问题的全过程，是学数学、用数学的过程。

例如：在初三年级我设计了这样一个数学实践活动：我把学生带到学校的一个池塘旁，要求学生利用所学过的数学知识测量池塘的宽度（要求学生根据所学知识设计两种测量方案，画出测量示意图，并简要说明测量方法和计算依据）。

为了帮助学生理解题意、突破难点、明确探究方向，我出示了一种设计方案：勾股定理法（如图1）。此方法的出示，一石激起千层浪，很快学生们就得到了如下几种测量方法（如图2～5）：（1）利用全等三角形的性质；（2）利用相似三角形的性质；（3）利用三角形的中位；（4）利用直角三角形中30°的锐角所对的直角边等于斜边的一半；（5）利用对称。

图1

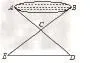
图2

图3

图4

图5

总之，数学教学的出发点和落脚点就是使学生学数学、用数学，培养学生解决实际问题的能力。这就需要我们广大数学教育者不断研究、反思、创新我们的教学，在数学教学过程中坚持以学生为主体，发展学生数学思维，提高学生数学能力。

book=74,ebook=76