非线性动力学教学中的混沌系统推广与仿真

贾强 孙梅

摘 要：以非线性动力学中典型的洛仑兹系统与埃农映射为例，通过引入各类不同的非线性，构造出更多有趣的混沌系统。利用基于MATLAB的数值仿真，进一步验证了本方法的有效性。该方法寓教于乐，有助于提升学生学习本课程的兴趣，同时为混沌应用提供更多的混沌模型。

关键词：混沌；MATLAB；洛仑兹系统；埃农映射；仿真

中图分类号：G642 文献标志码：A 文章编号：2096-000X（2017）23-0015-03

Abstract： Taking two chaotic prototypes in nonlinear dynamics， the Lorenz system and Hénon map， as examples， this work constructs diverse interesting chaotic models by introducing different nonlinearity functions. The numerical simulations based on MATLAB software further demonstrate the validity of our proposed techniques. It is conducive to the enhancement of the students' interest and presents more chaotic models for the application of chaos as well.

Keywords： Chaos； MATLAB； Lorenz system； Henon map； simulation

非线性动力学是一门面向高年级本科生和研究生的重要课程，在数学、物理、经济学、工程等多个学科的建模与分析中具有重要应用。大多数非线性动力学教材中，混沌的数学概念抽象而复杂，大多工科专业的学生难以理解。即便是数学专业的学生，要理解混沌的真正定义也并非易事。因而，在实际应用中用数学方法判断是否存在混沌现象非常困难。

随着数值算法的发展，基于软件的数值仿真为判断混沌提供了有力工具，同时为研究非线性模型并探究混沌现象提供了极大方便[1]。本文将枯燥的数学课程与计算机仿真相结合，寓教于乐，使学生真正参与课堂教学。著名非线性科学学者陈关荣教授曾撰文指出，若一个非线性系统的解有界，但不收敛也不发散，则该系统为混沌系统[2]。这意味着混沌系统一定具有混沌吸引子，其解为相空间中既不收敛到某点也不趋于无穷的杂乱曲线。依据这一特点，本文从非线性动力学常见的混沌模型出发，通过对不同非线性因素进行建模，引入非线性函数，构建新的混沌系统；同时利用软件MATLAB对新系统进行仿真，验证其混沌行为。通过设计课堂教学，提升学生动手能力，提升学生的学习兴趣与分析问题的能力；同时还提出更多新颖的混沌系统，为研究混沌理论及混沌应用提供更多的数学模型。

尽管已有不少关于混沌系统仿真的论文[3]，但通常只考虑经典的连续混沌系统，如洛仑兹系统[2]等，这些系统多为多项式函数，仿真也较简单。但很多实际工程问题可能包含更复杂的非线性，如时变参数、状态延迟或分段线性等。这些常见混沌系统却不能刻画这些复杂情形。一个有意义的问题是，这些非线性因素会对已有模型的动力学产生何种影响，而现有研究对该问题的关注却非常少。

本文将对该问题展开分析，对实际问题中不同的非线性因素进行建模，并将这些非线性引入常见混沌系统，利用MATLAB软件对所得新系统进行数值仿真。研究表明，所得新系统仍可能具有混沌行为。因此本文所提出的思想与新模型都值得关注。

一、实例（一）时变洛仑兹系统

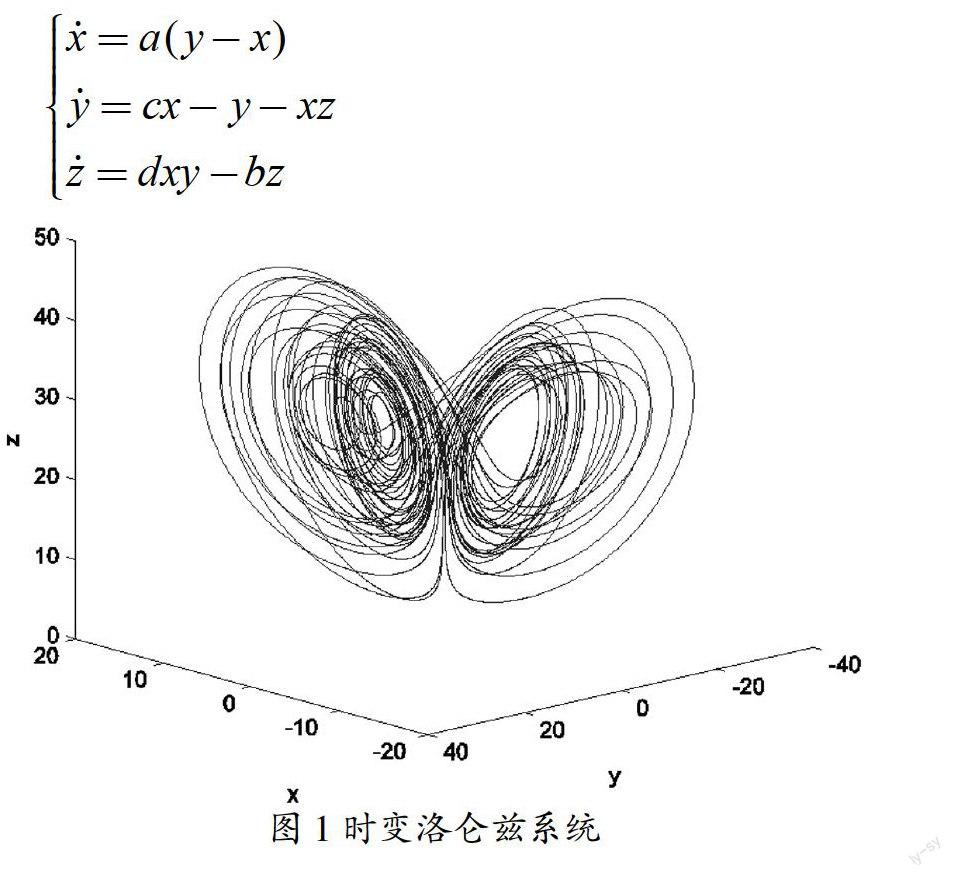
洛仑兹系统是美国气象学家洛仑兹教授于十九世纪六十年代建立的大气对流模型，可用如下微分方程组表示

其中a，b，c，d为参数。给定某些参数，如a=10，c=28，b=■，d=1，该系统具有混沌解，意指其数值解在相空间为一个蝴蝶形状的吸引子，如文献[3]所研究的情況。但在很多实际问题中，由于外界的干扰，系统的参数并非恒定不变的。时变参数更能刻画系统的真实动力学。若假定原系统的参数d随时间变化，令参数d为时变函数d（t）=1+3sin2（t），可得到一个新混沌系统。利用MATLAB中的ode45命令求解所得时变微分方程，得到系统具有图1所示混沌吸引子。与原系统对比发现，新系统的解轨道更加复杂。事实上，引入时变参数可使得系统的维数由三变为，图1中的三维图形为时变洛仑兹系统的吸引子在三维空间的投影，因而更加复杂。

二、实例（二）含分段线性的时变洛仑兹系统

关于混沌的最新研究发现，混沌系统中的某些非线性项可利用分段线性函数进行替换，而由此得到的新系统仍具有原系统的混沌特性。文献[4]表明，用分段线性函数替换一个四维超混沌系统中的某些交叉乘积项，所得的新系统的结构更加简单，但其动力学依旧具有混沌行为。该方案对于简化混沌电路的设计以及分析非线性系统的性质等问题具有重要价值。

下面将该方法应用于实例（一）中的时变洛仑兹系统中，用简单的符号函数替换第三个方程中乘积项的变量y，得到如下含有分段线性函数的系统。

由于该系统的符号函数sgn（y）只取正号或负号，原时变洛仑兹系统第三个方程中的状态乘积项简化为线性项 +x或-x，而所得新系统仍处于混沌状态。利用MATLAB进行仿真，用函数sign（y） 即可实现该分段线性函数，系统的混沌吸引子如图2所示。由此可见，新系统仍具有混沌动力学。

三、实例（三）延迟洛仑兹系统

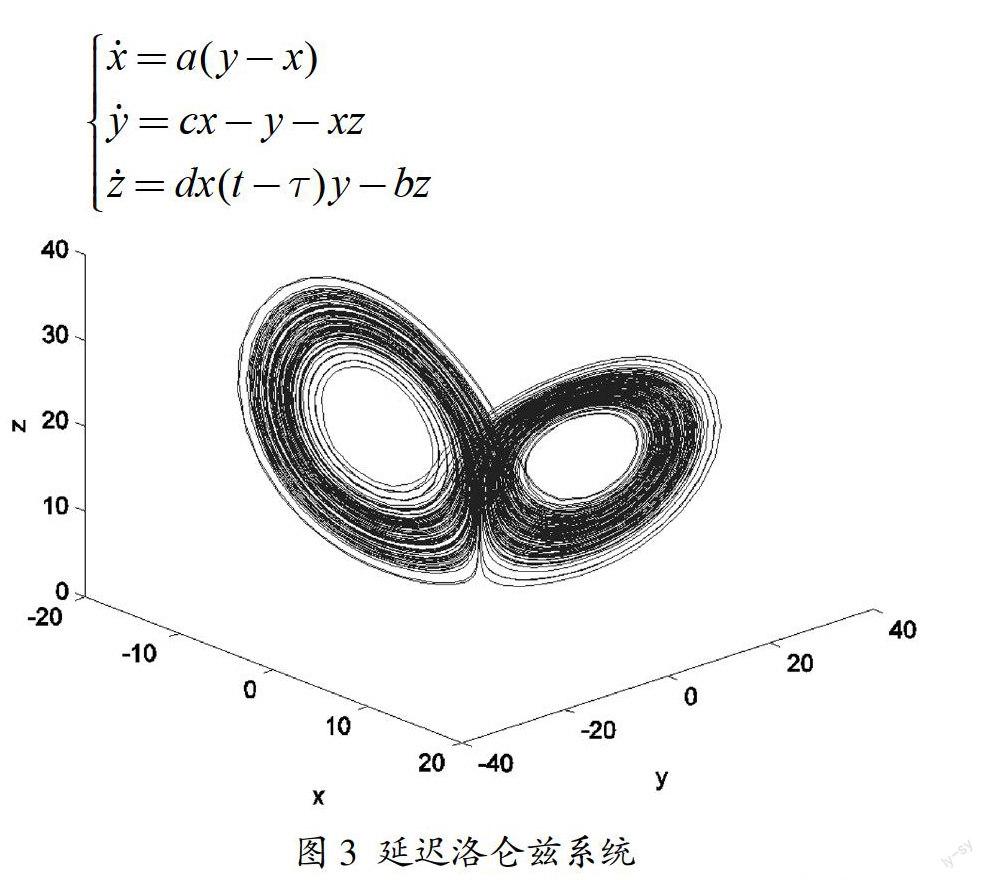
延迟现象广泛存在于各类工程问题，在系统建模中不可忽略。本文考虑如下具有延迟效应的洛仑兹系统

现有研究已表明，当c=20，d=1，？子=0时，洛仑兹系统具有稳定的平衡点。在实际问题中，由于复杂环境的干扰或特意设计，系统中可能出现某个状态的延迟。为了刻画这一问题，建立上述含有延迟项的方程组，即第三个方程右边的状态x具有延迟，由此得到一个新的延迟系统。事实上，若系统没有延迟，在前述参数下，系统具有稳定解，即从任意的初始条件出发，系统的解将收敛到某个稳定平衡点。新系统中由于存在状态延迟，其解不再收敛到平衡点，而是表现为混沌吸引子。数值仿真表明存在很多延迟值，确保系统出现混沌行为。利用MATLAB中的dde23命令，求解上述具有常数延迟的微分方程组。上述延迟洛仑兹系统当？子=0.05时的混沌吸引子如图3所示。根据泛函微分方程理论可知，该延迟系统为含时滞的泛函微分方程，实为一个无穷维动力系统，其动力学比原系统更加复杂。该例说明，在很多实际问题中，延迟现象对系统动力学的影响不可忽略，需要具体问题具体分析。

四、实例（四）含双曲函数的洛仑兹系统

值得说明的是，除了符号函数外，其他很多复杂的函数如指数函数、三角函数、双曲函数等都可用于构造混沌系统，而且这些函数都可用电子电路进行硬件实现。本例将双曲正弦函数应用于洛仑兹系统，得到如下的新混沌系统。

由图4可知，该系统的吸引子与以上各系统的吸引子具有不同的拓扑结构，但仍为混沌吸引子。

通过以上多个实例我们知道，洛仑兹系统在引入不同的非线性因素后，仍可能具有混沌现象。这表明对实际问题中的非线性因素进行建模，可能得出不同的混沌系统。虽然这些新系统与原系统在数学形式上有所不同，但都具备相同的混沌特性。

以上針对洛仑兹系统的讨论与推广有助于学生理解混沌系统的概念与性质，同时也引发他们对本门课程的强烈兴趣。进一步研究表明，其他常见混沌系统也可进行类似的推广，得到有趣的混沌模型。下面将对非线性动力学中的另一著名混沌系统——埃农映射进行讨论。

五、实例（五）时变埃农映射

前面几个实例考虑了连续时间系统，其解为相空间的连续杂乱曲线。本例考虑著名的二维离散混沌系统——埃农映射，其数学表达式为

其中a，b为参数。当a=1.4，b=0.3时，该映射具有月牙形的混沌吸引子。这里考虑用时变参数an=1.1+0.1sin（n）代换原参数a，得到一个新的埃农映射，其每步迭代中参数值与迭代次数有关。利用MATLAB中的for循环，易得该时变映射的混沌吸引子如图5所示。可见新系统的吸引子与原系统的吸引子形状类似，但其边界更加模糊，表明由于时变参数的存在，系统的动力学行为更加复杂。

六、实例（六）分段线性的埃农映射

类似于例（二）的方法，我们考虑在埃农映射中引入不同的分段线性函数，如绝对值函数，进而得到如下的分段线性模型

该分段线性映射中不含高次项，形式更简单。用MATLAB进行仿真，可得新映射系统在同样参数下仍具有混沌吸引子。该吸引子与原系统的吸引子相比，在相空间占有较小的区域，却没有任何周期现象，如图6所示。

本文的讨论与推广混沌系统的方法为非线性动力学课程的教学与研究提供了新思路，方便在课堂教学中加以利用，用于鼓励学生自己动手建模，并利用数学软件对混沌系统的性质进行分析。这无疑有助于激发学生学习非线性动力学课程的兴趣，并培养他们分析非线性系统的能力；同时本文也给出多个新的混沌系统，为混沌的理论与应用提供了借鉴。

参考文献：

[1]宁桂英，霍海峰.关于MATLAB软件在线性代数教学中的应用探讨[J].科教文汇，2015（313）：49-50.

[2]陈关荣，吕金虎.Lorenz系统族的动力学分析、控制与同步[M]. 北京：科学出版社，2003.

[3]吴卫华，等.Lorenz混沌系统的分析与电路实现[J].大学物理实验，2014，27（2）：41-43.

[4]Li， C.， Sprott， J. C.， Thio， W. and Zhu H. [2014] A new piecewise linear hyperchaotic circuit，" IEEE Trans. Circuits and Syst.-II， Exp. Briefs， vol. 61， no. 2， pp. 977-981.