基于改进仿电磁学算法的多目标电网规划方案研究

程乐园，党彬，王鑫，刘伟，张艳来，郭和强

（1.国网安阳供电公司，河南安阳 455000；2.天津天大求实电力新技术股份有限公司，天津 300384）

电网规划内容主要是对输电网和配电网进行规划，规划的目的就是在满足系统和负荷安全运行的前提下，通过一系列衡量指标保证网架的最优解[1-3]。传统的优化算法如最短路径法[4]、非线性规划法[5]等，很难满足电网规划中大规模组合数学问题的优化分析，易造成“维数灾”[6]问题。近些年来，智能优化算法在最优解计算方面表现出良好的寻优速度和计算性能，得到了广泛应用，包括遗传算法（genetic algorithm，GA）[7]、粒子群算法（particle swarm optimi⁃zation，PSO）[8-10]、蚁群算法（ant colony optimization，ACO）[11]、仿电磁学算法（electromagnetism-like mech⁃anism，ELM）[12-13]等，有效地满足了电网规划决策中寻求最优解的问题，但这些算法同时也存在参数敏感、效率低等缺陷[14-16]。采用ELM算法通过对电网规划寻优过程离散化处理，实现规划方案的可靠性和经济性，但ELM在寻求最优解中忽视了种群的分布多样性，易出现局部最优、迭代不收敛的问题[17-18]。基于此，本文利用改进策略来弥补仿电磁学算法缺陷，通过建立多目标模型，提高其在大规模离散组合中的寻优性能。

1 基于基本ELM的改进分析

1.1 ELM的基本原理

ELM算法是一种模拟带电电荷相互作用提出的一种全局优化算法[19]。ELM中将粒子作为一种带电体，利用相应粒子的适应度函数值赋予粒子虚拟电荷量来模拟粒子间的矢量力，由库克定律计算出各粒子间的矢量力，通过粒子团指定的总矢量力方向来寻求新种群。

ELM算法寻优过程中的带电粒子都存在潜在解，将初始种群中的带电粒子带入目标函数中，获得相应的电荷量，根据电衡量大小来判断带电粒子的优劣度。粒子虚拟电荷量计算表达式为

式中：分别为第k次迭代的第i个粒子和对应的最优粒子；m、n分别为仿电磁学算法中的种群集合和粒子维度数；为第i个粒子在第k次迭代中的虚拟电荷量，随着目标函数减小，会不断增大。

粒子群的总矢量力可由式（2）中计算式给出，求得粒子总矢量力值。

式（3）描述了与的接近程度，值越大，则表明越接近最优解；表示粒子的总矢量力，是种群受力性质的反应，当，则粒子i、j为引力，反之则粒子间表现为斥力。

在由m个粒子构成的解域中，通过迭代算法寻求最优解，带电粒子按照式（4）中的移动规则来实现种群中粒子更新：

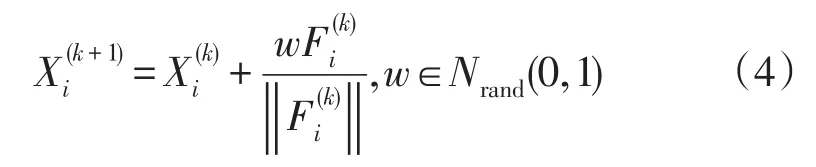
1.2 ELM的改进策略

1.2.1 改进的抗干扰种群

对传统ELM的种群搜素分析可知，当粒子间表现为引力时，则粒子向优化区聚集，当粒子间表现为斥力，则粒子将会进入未搜索区域。然而，这种粒子间的区域扩展和优化只是一种基于粒子个体间的领域搜索，无法对群体展开优化扩展，因此寻求最优解过程中可能导致局部最优解。基于此，本文采用被动聚集思想[20]，以单个粒子为对象，考虑粒子群对单一粒子的影响因素和粒子间的相互作用力，对式（4）进行改进为

式中：为粒子i对种群中随机粒子r的虚拟电荷作用力；c为被动聚集因子，当，取值为负，反之则取正值；δ为抗干扰因子；R为约束条件，其是为了保证搜索区域能够在特定的区间范围内，R存在的关系式为

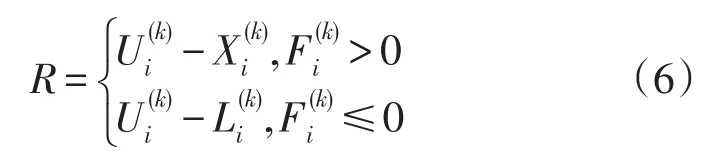
式中：分别为的上限值和下限值，这样就保证了算法在有效区域内。同时，改进模型有效地提高了全局寻优能力。

1.2.2 自适应变异策略

基本ELM算法中忽略了种群的多样分布性，导致收敛速度下降，并可能出现局部最优现象[21]。对于种群的多样性问题，通过引入正态分布和中心极限定理来加以改善，对于种群中的粒子，带电荷量越大，则产生的变异量就越小。式（7）为寻优过程中各粒子遵循的变异方式：

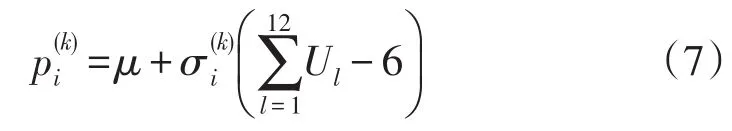
式中：为的变异量；为标准差；μ为该正态分布的数学期望。当确定了粒子电量区间后，便能保证算法具有较高的抗局部极值能力，实现种群多样性算法。

1.2.3 权重自适应控制

ELM算法中对计算参数的调取是保证算法速度的重点。在迭代算法后期，由于权重因子存在随机性，往往会造成不收敛现象，其大小对于实现算法的全局搜索和局部细化有决定性作用。基于此，引入自适应函数式（8）来满足算法的全局搜索和收敛性。

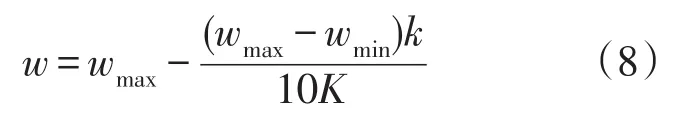
式中：wmax为迭代初期算法权重中；wmin为迭代末期算法权重；k为当前迭代数；K为算法总的迭代数。

2 IELM在多目标电网规划方案的模型构建

2.1 目标函数及其约束

传统电网规划方案中经济性仍然是衡量方案优劣的一个主要指标。本文主要考量经济性指标和可靠性指标来进行方案校验，构建的目标模型包括电网投资、网络损耗、停电损失等经济性指标，具体的表达式为

式中：minF1和minF2分别为电网投资运行费用目标函数和电网维护、改造检修费用目标函数；xd为线路数；ad为线路单位造价；γ为线路折率；C为线路网损；Pj、Uj、Rj分别为线路运行中的功率、电压和电阻；Sld为线路运行负荷的集合，L为线路中的负荷节点数；为线路故障率；Pl为线路出现该功率的概率值。

对于线路出现大规模故障而造成线路瘫痪问题，线路各侧设备s、t的停运率同样可由式（10）来表达：

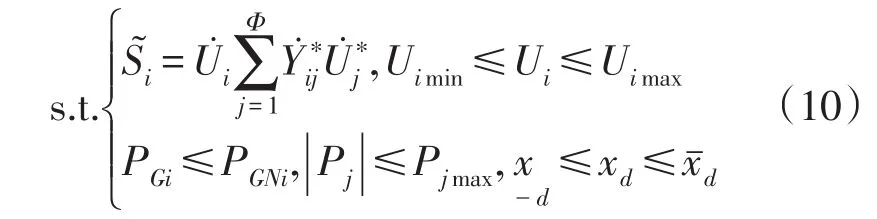
式中：Φ为线路中的节点数；Uimax、Uimin为i节点的电压上、下限极值；PGi、PGNi和Pj、Pjmax分别为电源侧（如发电机）和线路侧的有功和极值；为线路d的架线极值。

2.2 多目标模型归一化

在目标函数F1、F2中，可靠性和成本间存在着固有矛盾，且未考虑系统的N-1安全准则。为此，本文采用加权法来获得合适的全系统，对多个矛盾的目标函数应用相同的度量进行协调，得到电网规划方案的优劣。转化后的模型为

式中：Mk为k阶段惩罚系数；NLk为网络初始化一直到k阶时的总线路回数；NFk为检修维护时需断开回路数；为第l条线路断开时支路j的有功值和极限值。

配合IELM算法在极值问题上的求解特点，构造同一度量体下的评价函数为

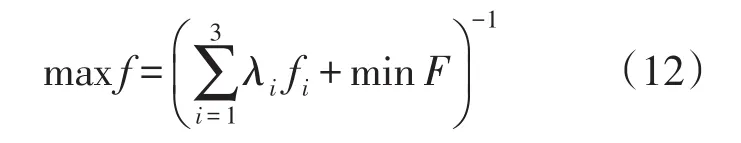
式中，λi为权系数。若多个Xi均能满足函数f取得最小值，则需进一步搜寻最优解。

2.3 IELM在多目标电网规划实现

2.3.1 编码决策变量

通过上述分析可知，传统电网的规划是离散型的。考虑到电网整数性，本节引入十进制方式来实现对进行编码：

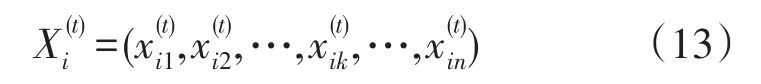
式中，为进行t次迭代时粒子k在线路走廊d中的回路数。对粒子进行编码后，需对每一代新种群进行等概率离散化处理，以便符合电网规划中整数离散化需求，根据式（14）进行离散化处理：

式中，Mround为取整函数，实际计算过程中按四舍五入取整数，当超过极限值时则取极值。

2.3.2 种群的初始化

为保证编码决策变量给出的约束条件与种群粒子相符，同时满足种群的均匀性、多样性和一定的覆盖率，对种群进行等概率初始化：

将种群中的粒子数代入式（15），重复运用等概率处理方法进行迭代计算，获得m个个体和相应的n个变量共同组成一个矩阵Am×n，实现对种群区域的全覆盖，满足种群多样性、分布性的需求。

当设置种群收敛判据的迭代次数T时，需考虑算法可能造成的解的效率问题。迭代次数设置过高，则算法迭代效率下降，而次数过小，则可能得不到所需要的全局最优解。为避免计算过程中出现阻滞于局部极值点，在确定停滞代数Tmax时，采用种群间表现出的差异化来作为算法的收敛判据：

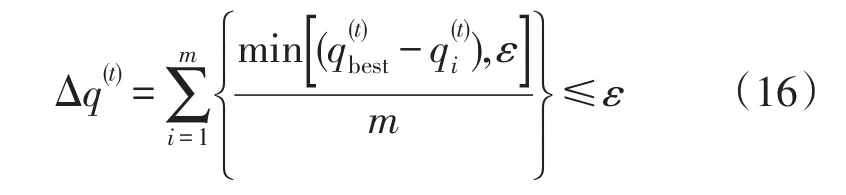
当种群中的粒子与最优粒子性能差异在ε范围内时，则算法收敛。

2.3.3 IELM的执行程序

1）设置种群规模参数m，解群差异性指标ε，决策变量wmax、wmin等参数，并进行初始化。

2）计算等粒子参数值，寻求最优粒子。判断最优粒子性能差异在ε范围内，若成立，则执行式（7），利用式（6）获得新种群；否则回到式（6）计算。

3）判断种群进化是否达到最大进化代数，若满足条件，则输出“不收敛”计算结果；若进化进入停滞代数，则实行变异策略。

4）迭代终止，得到和相应的函数，通过对进行解码获得电网规划最优解。

3 算法实例验证

利用图1中的18节点初始网络系统进行IELM算法的测试。系统原设10个节点，现在需增加到18个节点。系统基准功率100 MV·A，系统中的各节点和相应负荷参见文献[22]，采用2×LGJ-300线路型号。

图1 系统的初始网络Fig.1 The initial network of the system

基于Matlab测试平台进行防治运算，表1为选定的可靠性测试指标。

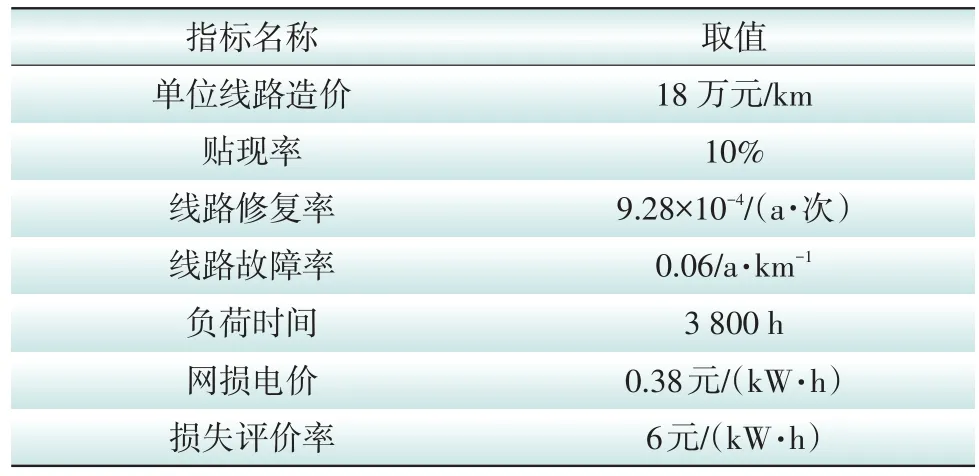
表1 节点系统的指标Table 1 The index of the node system

为检验方案的优越性，将本文确定的全系统与原始全系统进行计算比较，获得的结果见表2所示。

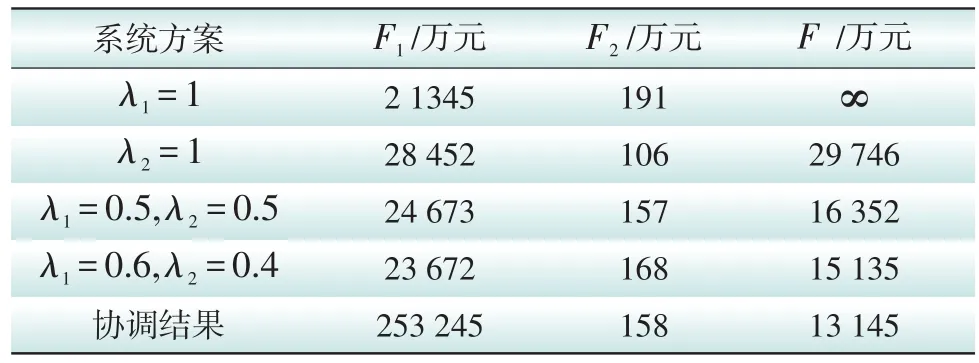
表2 节点系统计算结果Tab.2 The calculation results of the node system

通过IELM的逐步求解分析，获得解码后的电网规划方案如图2所示。

图2 节点系统的网络优化结构Fig.2 Network optimization structure of the node system

从表2中获得的数据分析可知，在保证电网运用经济型运营成本时，缺电成本出现了增长，而降低缺电成本后，虽然保证了电网规划方案的可靠性，但运用成本又有所提升。因此这都不是获得的最优解。同时，电网方案实际应用中，更侧重于对经济型的要求，而采用IELM算法保证了电网方案的经济型指标在建立模型的误差范围内，且基于本文所建立的全系统在满足最优解的经济性约束时，同样保证了方案的可靠性。此外，利用IELM建立的电网规划最优方案同时保证了电网架构的N和N-1安全。

为验证IELM在求解多目标电网规划优选方案的有效性，选择一个有46节点系统作为对比对象，该系统当前有46条输电线路，预计3年内增加至76条。2个测试系统的参数信息见文献[23]。设权重系统λ1=0.5、λ2=0.2、λ3=0.3，分别引入IELM和GA算法对2种不同的系统求解。对比结果见表3和图3。

表3 不同算法的结算结果对比Fig.3 Comparison of results of different algorithms

图3 不同算法收敛曲线对比Fig.3 Comparison of convergence curves of different algorithms

从图3中可以看出，采用IELM算法有效地避免了GA算法在进化后期存在的收敛振荡问题，且IELM具有更高的寻优效率。GA算法中，设定种群规模和迭代次数均2倍于ELM算法时，所得到解仍然出现局部最优，而IELM不管是初始种群规模，或者是设计的迭代次数均低于GA算法，计算结果的获优率却高于GA算法，在节省预算空间和时间的同时，容错率更高。

4 结语

1）基于基本ELM在求解电网规划方案中存在的解域狭小，引入被动聚集思想来实现单个粒子的解域拓展；针对算法迭代后期的不收敛性、易限于局部收敛，建立了权重的自适应控制函数；为避免算法出现早熟收敛，运用搜索范围动态缩减法来满足预期收敛速度和全局寻优效果。

2）IELM算法有效提高了基本ELM算法的抗局部极值能力和全局寻优效率，算法可以考虑多种目标函数和约束条件，获得的最优解具备优良的收敛性，能有效兼顾多目标电网规划中的可靠性和经济性因素，为多目标电网规划方案提供了一个全新的全局优化算法。

3）相较于GA算法等，采用IELM算法在解决电网规划方案的非线性组合优化过程中，在收敛效率、操作适应性和全局最优解方面具有显著优势，为大规模电网规划优化问题的求解开辟了一条新途径。

参考文献

[1]谭颖，吕智林，李捷.基于改进ELM的风/光/柴/储独立微网分布式电源多目标容量优化配置[J].电力系统保护与控制，2016（8）：63-70.TAN Ying，LÜ Zhilin，LI Jie.Based on the improved ELM wind/light/wood/store independent micro network distribut⁃ed power multi-objective optimal allocation of capacity[J].Power System Protection and Control，2016（8）：63-70.

[2]姜惠兰，安星，王亚微，等.基于改进NSGA2算法的考虑风机接入电能质量的多目标电网规划[J].中国电机工程学报，2015（21）：5405-5411.JIANG Huilan ，AN Xing，WANG Yawei，et al.Based on the improved NSGA2 algorithm considering the fan power quality access to the network planning multi-objective[J].Proceedings of the CSEE，2015（21）：5405-5411.

[3]宋春丽，刘涤尘，吴军，等.基于改进和声搜索算法的电网多目标差异化规划[J].电力自动化设备，2014（11）：142-148.SONG Chunli，LIU Dichen，WU Jun，et al.Based on the improved harmony search algorithm of the multi-objective differential of transmission network planning[J].Electric Power Automation Equipment，2014（11）：142-148.

[4]王世亮.基于改进量子粒子群算法的智能电网多目标优化规划研究[D].兰州：兰州理工大学，2014.

[5]孔祥聪，周步祥，汝锐锐，等.改进GAAA算法在多目标电网规划中的应用[J].电力系统及其自动化学报，2013（6）：112-116.KONG Xiangcong，ZHOU Buxiang，RU Ruirui，et al.Improved GAAA algorithm in the application of multiobjective planning[J].Proceedings of the CSU-EPSA，2013（6）：112-116.

[6]李鹏，刘成斌，姜涛，等.智能电网下的电网安全性与稳定性[J].电网与清洁能源，2013（2）：33-37，42.LI Peng，LIU Chengbin，JIANG Tao，et al.The safety and stability of power grid under smart grid[J].Power System and Clean Energy，2013（2）：33-37，`42.

[7]伍力，吴捷，钟丹虹.多目标优化改进遗传算法在电网规划中的应用[J].电力系统自动化，2000，（12）：45-48.WU Li，WU Jie，ZHONG Danhong.Multi-objective opti⁃mization genetic algorithm is improved in the application of the power grid planning[J].Automation of Electric Power Systems，2000（12）：45-48.

[8]王金全，黄丽，杨毅.基于多目标粒子群算法的微电网优化调度[J].电网与清洁能源，2014（1）：49-54.WANG Jinquan， HUANG Li， YANG Yi.Microgrid optimizationschedulingbasedonmulti-targetparticleswarm optimization[J].Power System and Clean Energy，2014（1）：49-54.

[9]吴欣，盛四清，曹林.基于改进简化粒子群算法的多目标输电网规划[J].陕西电力，2012，（05）：30-33，47.WU Xin，SHENG Siqing，CAO Lin.Based on the improve⁃ment of multi-target transmission grid planning for the sim⁃plified particle swarm algorithm[J].Shaanxi Electric Pow⁃er，2012（5）：30-33，47.

[10]曹承栋，常鲜戎，刘艳.考虑地理因素的改进量子粒子群算法在多目标电网规划中的应用[J].电网技术，2012（3）：134-139.CAO Chengdong，CHANG Xianrong，LIU Yan.Consider the geographical factors of improved quantum particle swarm optimization（pso）algorithm in the application of multi-objective planning[J].Power System Technology，2012（3）：134-139.

[11]符杨，孟令合，胡荣，等.改进多目标蚁群算法在电网规划中的应用[J].电网技术，2009（18）：57-62.FU Yang，MENG Linghe，HU Rong，et al.Improved multi-objective ant colony algorithm in the application of power grid planning[J].Power System Technology，2009（18）：57-62.

[12]吴杰康，郭壮志.基于仿电磁学算法的梯级水电站多目标短期优化调度[J].中国电机工程学报，2010，30（31）：14-21.WU Jiekang，GUO Zhuangzhi.Electromagnetism-like mechanism based multi-objective short-term optimization scheduling for cascade hydro plants[J].Proceedings of the CSEE，2010，30（31）：14-21.

[13]王学友，周步祥，付锦，等.分布式电源优化配置的仿电磁学算法[J].电力系统及其自动化学报，2012，24（4）：134-138.WANG Xueyou，ZHOU Buxiang，FU Jin，et al.Electromagnetism-like mechanism based on optimal placement of dis-tributed generation[J].Proceedings of the CSUEPSA，2012，24（4）：134-138.

[14]何永秀，朱茳，罗涛，等.城市电网规划自然灾害风险评价研究[J].电工技术学报，2011，26（12）：205-210.HE Yongxiu，ZHU Jiang，LUO Tao，et al.Risk assess⁃ment of natural disaster in urban electric power network planning[J].Transactions of China Electrotechnical Soci⁃ety，2011，26（12）：205-210.

[15]刘旭娜，肖先勇，汪颖，等.用户友好电网规划模型与方法的研究[J].电力系统保护与控制，2010，38（23）：196-202.LIU Xuna，XIAO Xianyong，WANG Ying，et al.The study of programming model and method of customer friendly power network[J].Power System Protection and Control，2010，38（23）：196-202.

[16]王茜，张粒子，舒隽，等.基于阈值选择策略的改进混合蛙跳算法在电网规划中的应用[J].电力系统保护与控制，2011，39（3）：34-39.WANG Qian，ZHANG Lizi，SHU Jun，et al.Application of improved shuffled frog leaping algorithm based on threshold selection strategy in transmission network planning[J].Power System Protection and Control，2011，39（3）：34-39.

[17]付锦，周步祥，王学友，等.改进仿电磁学算法在多目标电网规划中的应用[J].电网技术，2012，36（2）：141-146.FU Jin， ZHOU Buxiang， WANG Xueyou， etal.Application of improved lectromagnetism-like mechanism in multi-objective power network planning[J].Power System Technology，2012，36（2）：141-146.

[18]王淳，万卫，程虹，等.多阶段输电网络最优规划的模拟植物生长算法[J].高电压技术，2009，35（4）：937-942.WANG Chun，WAN Wei，CHENG Hong，et al.Plant growth simulation algorithm for the optimal multistage transmission network planning[J].High Voltage Engineering，2009，35（04）：937-942.

[19]顾洁，秦玥，包海龙，等.基于熵权与系统动力学的配电网规划动态综合评价[J].电力系统保护与控制，2013，41（1）：76-83.GU Jie，QIN Yue，BAO Hailong，et al.Comprehensive and dynamic evaluation ofthe distribution network planning based on entropy weight and system dynamics[J].Power System Protection and Control，2013，41（1）：76-83.

[20]韩晓慧，王联国.输电网优化规划模型及算法分析[J].电力系统保护与控制，2011，39（23）：143-148，154.HAN Xiaohui，WANG Lianguo.Review of transmission network optimal planning model and algorithm[J].Power System Protection and Control，2011，39（23）：143-148，154.

[21]李鑫滨，朱庆军.一种改进粒子群优化算法在多目标无功优化中的应用[J].电工技术学报，2010，25（7）：137-143.LI Xinbin，ZHU Qingjun.Application of improved particle swarm optimization algorithm to multi-objective reactive power optimization[J].Transactions of China Electrotechni⁃cal Society，2010，25（7）：137-143.

[22]毛玉宾，王秀丽，王锡凡.多阶段输电网络最优规划的遗传算法[J].电力系统自动化，1998，22（12）：13-19.MAO Yubin， WANG Xiuli， WANG Xifan.Genetic algorithm for the optimal multistage transmission network planning[J].Automation of Electric Power Systems，1998，22（12）：13-19.

[23]石立宝，徐国禹.基于自适应进化规划的电网多目标优化运行[J].中国电机工程学报，2000，20（8）：31-36.SHI Libao，XU Guoyu.A new method of self-adaptive evo⁃lutionary programming on multi-objective optimal opera⁃tion of power system[J].Proceedings of the CSEE，2000，20（8）：31-36.