配电网投资分配的模型策略
余松,吴延琳,王主丁,张漫
(1.国网陕西省电力公司,陕西西安 710048;2.国网陕西省电力公司经济技术研究院,陕西西安 710048;3.重庆大学,重庆 400044)
为了满足社会对电力的需求,供电企业每年都会投入大量的资金用于配电网的建设,而地区的差异性及发展的不平衡性给配电网的投资决策带来了一定的困难。因此,在投资额给定的情况下,建立合理的投资决策模型,有利于为各地区的投资决策提供科学的依据,规范决策部门的决策及管理行为,提高资源的利用率,提升投资的经济及社会效益。同时,在目前的体制下,各个供电局为了追求自身效益最大化,上报的项目往往较多,这也要求对配电网建设投资的分配进行科学和独立的评估。
目前,针对配电网资金在不同地区之间的合理分配,较为直观的方法是借助配电网规划成果对相应投资规模进行估算[1-4],但由于工作量大不适用于项目众多且情况较为复杂的中低压配网投资决策。其他方法大多是基于评估体系的配电网投资分配决策[5-10],此类方法评估侧重点不同时,评估结果相差较大。另外,文献[11]通过典型供电模式配电网规模的估算来进行投资分配决策,但考虑的因素有限。
本文基于现状配电网及其负荷增长对各地区配电网规模进行估算,并结合各地区配电网基本发展需要、投资的经济效益及社会效益对总投资分配进行决策。首先,提出刚性投资、经济投资、投资上下限、刚性需求和柔性投资的概念及计算方法;其次,基于配电网基本发展需要、投资的经济效益及社会效益等基本原则,提出4种实用的投资分配模型策略(即按基本投资占比分配、按等收益率分配、按电量需求占比分配和基于加权的综合分配);最后,以某省的投资分配案例验证所提出模型策略的实用性和有效性。提出的方法能在投资总额一定的情况下明确各地区的分配投资区间及分配方案,为决策者提供更全面的决策信息。
1 投资定义
首先对涉及配电网投资分配决策的相关投资定义如下。
配网总投资IA:可用于分配的配电网总投资。
经济投资:在售电量、电价及目标收益率一定的条件下,基于配电网内部收益率法反算的第i地区的配电网投资,用以评估投资的经济可行性。
基本投资:为满足第i地区现有负荷和新增负荷所需要新建和改造的基本电网规模投资,可由下述基本投资模型估算求得。
特殊刚性投资:为满足第i地区配电网某些硬性指标或者建设要求所需的投资(如涉及已纳入国家电网公司规划的项目和满足无电地区用电需求),根据地区发展需求由相关规划人员或专家给定。
应急投资:电网公司为适应应急需求而给第i地区预留的电网建设费用。刚性投资:第i地区的刚性投资,为该地区基本刚性投资、特殊刚性投资和应急资金之和。
投资下限:本文投资下限也叫刚性需求,为第i地区的刚性投资、规划投资与经济投资中的最小值为

投资上限:首先获得第i地区的规划投资与经济投资中的较小值,该较小值与相同地区刚性投资中的较大值定义为投资上限,如公式(2)所示。

不同地区投资上下限如图1所示(图中,各地区“刚性需求”为其投资下限,各地区“柔性需求”为其投资总额中大于相应刚性需求的那部分投资)。
刚性总需求:所有地区投资下限或刚性需求之和,如公式(3)所示。

式中m为规划区域的总地区数。
柔性总投资IF:满足刚性总需求外剩余可供分配的总投资,如公式(4)所示。

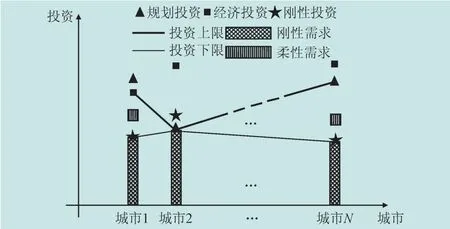
图1 各地区投资上下限取值示意图Fig.1 Diagram of upper and lower limit investments for different subordinate areas
2 基本投资估算模型
根据现有配电网规模及预测负荷计算配电网基本刚性投资。基本刚性投资分为新建投资和改造老旧设备投资,其中新建投资又分为高压配电网投资及中低压配电网投资,详细投资分类如图2所示。

图2 基本投资分类示意图Fig.2 Diagram of basic investment classification
2.1 新建投资
2.1.1 高压配网新建投资
由于每年的规划报告中高压项目相对较少且经过严格审查,其规划投资可信度非常高。因此,第i地区高压配网新建投资可直接由第i地区的规划报告获得。
2.1.2 中压配电网新建投资
1)中压线路新建投资
考虑到现有中压线路供电半径变化,第i地区中压线路新建投资为
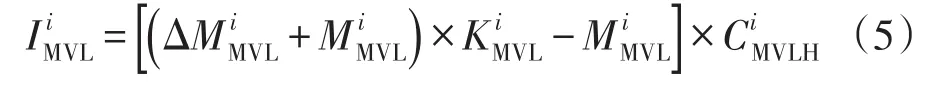
式中:和分别为第i地区现有和新增中压线路回数;为现状年平均的中压出线回路单价;为规划年和现状年中压线路供电半径的比值。
以中压线路目标负载率(一般为经济负载率,也可根据供区负荷密度或接线方式调整,如三供一备可取75%,负荷密度低的农村地区可以轻载,如取20%)为基准,超过该基准的负荷可转移到其他线路,低于该基准的线路容量裕度可带新增负荷或其他线路转移的负荷。因此,第i地区新增中压线路回数为
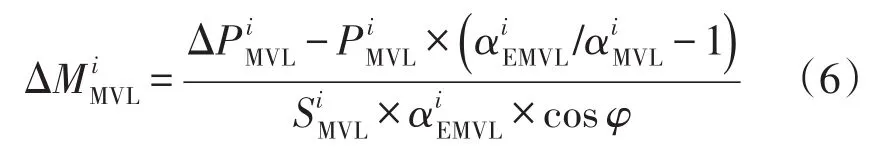
式中:和分别为新增中压负荷和现状年中压负荷;为每条中压线路平均容量;和分别为现状年中压线路平均负载率和线路目标负载率;cosφ为功率因素。注意:若根据式(6)算出的新增中压线路回数为负,让。
第i地区现状年平均的出线回路单价为
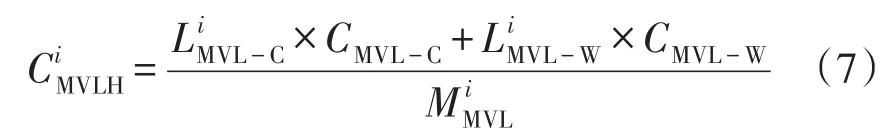
式中:为电缆线路长度;为架空线路长度;CMVL-C为电缆线路的平均长度单价;CMVL-W为中压架空线路的平均长度单价。
考虑到单座变电站的供电面积与其供电半径的平方成正比,规划年和现状年的中压出线供电半径的比值为
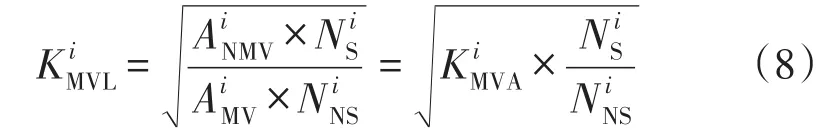
式中:和分别为现状年和规划年中压线路供电范围面积;和分别为现状年和规划年有中压出线的高压变电站个数;为与的比值。
2)配变新建投资
第i地区配变新建投资为
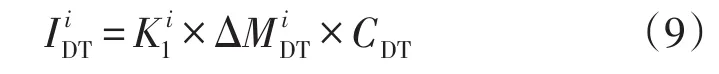
以配变目标负载率(一般为经济负载率,也可根据供区负荷密度调整)为基准,超过该基准的负荷可转移到其他配变,低于该基准的配变容量裕度可带新增负荷或其他配变转移的负荷。因此,第i地区新增配变台数为
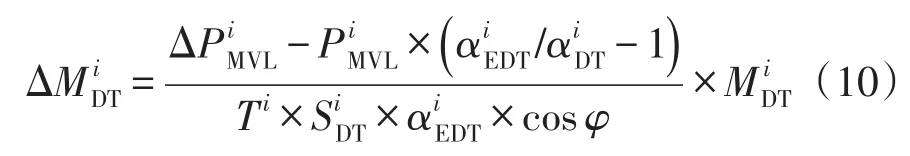
式中:和分别为现状年配变平均负载率和配变目标负载率;Ti为中压负荷相对于配变负荷的同时系数;为现状年配变总容量;为现有的配变台数。注意:若根据式(10)算出的新增配变台数为负,让
3)环网柜新建投资
第i地区环网柜新建投资为
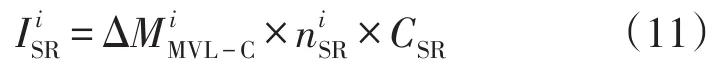
式中:为新增电缆回路数;CSR为每台环网柜的平均单价;为中压电缆线平均分段数。其中,为
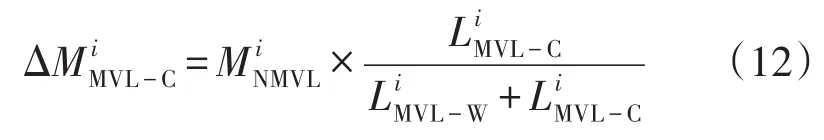
4)柱上开关新建投资
第i地区柱上开关新建投资为
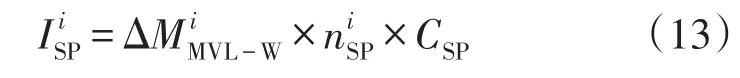
式中:为新增架空线回路数;CSP为每台开关的平均单价;为中压架空线平均分段数。其中,新增架空线回路数为
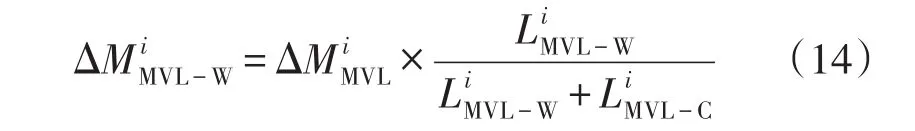
2.1.3 低压线路新建投资
第i地区低压线路新建投资为
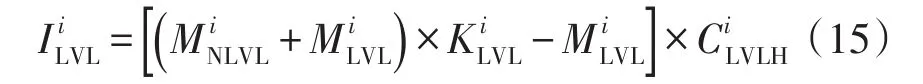
式中:和分别为现有和新增低压出线回路数;为现状年平均的低压出线回路单价;为规划年和现状年低压线路供电半径的比值。
类似新增中压线路回数计算公式,第i地区新增低压线路回数为
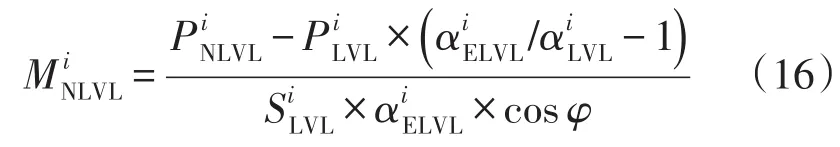
式中:和分别为新增低压负荷和现状年低压负荷;和分别为现状年低压线路平均负载率和线路目标负载率(一般为经济负载率);cosφ为功率因素;为每条低压线路平均容量。注意:若根据式(16)算出的新增低压线路回数为负,让。
低压出线回路单价为
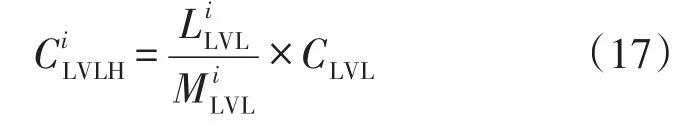
式中:为现有低压线路长度;CLVL为低压线路的平均长度单价。
类似中压出线供电半径变化率计算公式,为

式中:和分别为现状年和规划年低压线路供电范围面积(可近似认为与现状年和规划年中压线路供电范围面积和相同);为与的比值(可近似认为与相同)。
2.2 老旧设备改造投资
2.2.1 高压配网改造投资
类似高压配网新建投资,第i地区高压配网老旧设备改造投资可直接由第i地区的规划报告获得。
2.2.2 中低压配电网改造投资
若在每年的规划报告中,中低压项目基础数据(如使用年限、运行状况等)比较齐全,第i地区中低压配网旧设备改造投资可直接由第i地区的规划报告获得。否则,可采用以下的模型进行宏观投资估算。
若第i地区现状年电网规模采用最新设备单价计算的价值为,负荷平均增长率βi,新建项目投资可近似表示为现状规模价值乘上负荷增长率,如式(19)所示。

假定第i地区改造比例为改造投资与新建投资的比值,改造老旧设备投资为

改造设备投资包含了之前第N年的新建投资与改造投资为
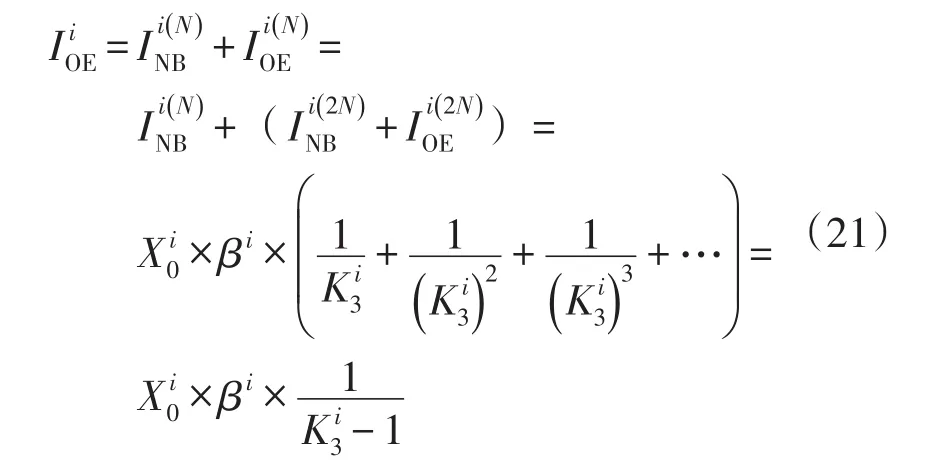
式中:为第N年电网规模价值;为某年规模与往前推第N年前电网规模的比值。
则改造比例为

改造比例与设备使用年限及负荷增长率βi关系如表1所示。
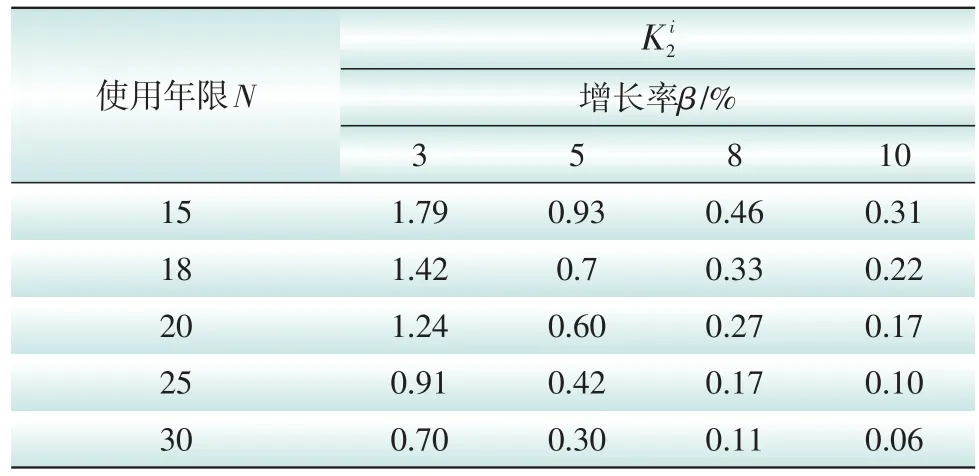
表1 改造比例K2i与设备使用年限N及负荷增长率βi的关系Tab.1 Reconstruction ratios related to equipment service life and load growth rates
由表1分析可知:当配电网设备使用年限变化范围为15~30 a、负荷增长率变化范围为3%~12%时,老旧设备改造比例变化范围为3%~179%;在负荷增长率一定的情况下,设备使用年限越长,老旧设备改造比例越低;在设备使用年限一定的情况下,增长率越高,老旧设备改造比例越低;由于中低压设备使用年限较短,负荷增长率较小,中低压老旧设备改造比例相对较高;高压设备使用年限较长,负荷增长率较快,因此老旧设备改造比例相对较低。
通过负荷增长率及设备使用年限可估算出各地区的设备改造比例,根据式(20)由新建投资及改造比例即可求得各地区老旧改旧设备投资。
2.3 基本投资汇总
综上所述,第i地区基本投资由新建投资与改造老旧设备投资构成,可表示为
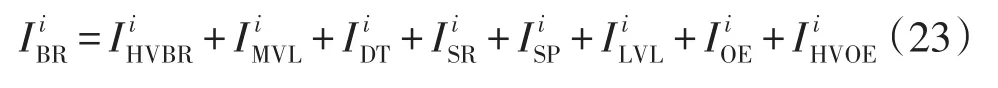
3 经济投资估算模型
本文经济投资计算方法是在售电量、电价及目标收益率一定的条件下,采用内部收益率法反算投资;而且一年投资(流出)只对应相应年份(一年)的增供电量(流入),但需要考虑投资使用年限内该增供电量总收入及投资折旧维护率。
针对某一年的配电网经济投资计算,经济流量模型如图3所示,各地区经济投资计算步骤如下。
1)根据式(24)计算各地区配电网售电平均净收益电价
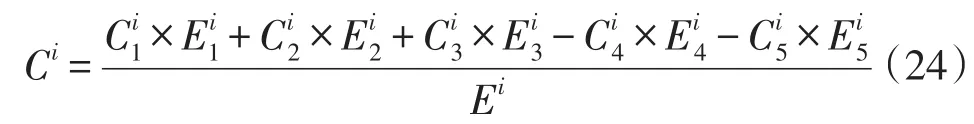
式中:Ci为第i地区的平均电价;Ei为第i地区的总售电量;和分别代表第i地区的工业售电量、商业售电量、居民售电量、水电购电量和火电购电量;和分别代表工业售电单价、商业售电单价、居民售电单价、水电购电单价和火电购电单价。
2)在电价已知的情况下即可计算第i地区现有售电收入:

第i地区新增售电收入为

3)现金流出为投资与折旧维护费用之和,假设地区的折旧维护率为γ,投资设备使用寿命为N年,为i地区包含基建、技改和小基建等当年所有投资,则根据复利公式现金流出为

4)将对应新增售电的N年收入与改造涉及的N年售电收入之和作为现金流入:

式中IRR为已知的内部收益率。
5)在第i地区配电网售电收入、改造比例、负荷平均增长率βi、内部收益率IRR及折旧维护率为γ为已知的情况下,利用公式(29)可反算各地区的。
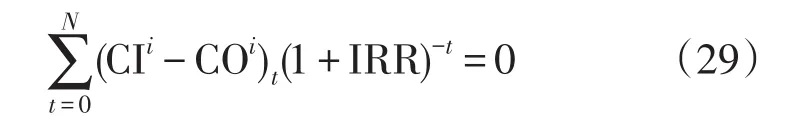
6)令第i地区电网建设投资占企业总投资比例为,配网投资占全网投资比例为,则第i地区配电网经济投资为

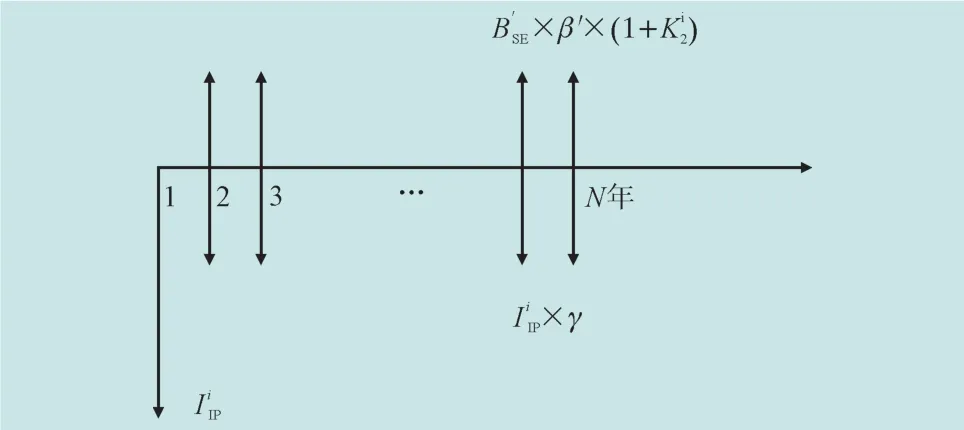
图3 经济流量模型示意图Fig.3 Diagram of economic flow model
4 投资分配模型策略
考虑到配电网基本发展需要、投资的经济效益及社会效益等基本原则,提出了几种投资分配的模型策略。
4.1 模型策略I
若整个规划区域可分配总投资IA小于等于刚性总需Imin,即柔性总投资IF小于等于0,则各地区分配投资额可按其投资下限的占比进行分配,此时第i地区投资分配额为

4.2 模型策略II
若柔性总投资IF>0,考虑到配电网基本发展需要、投资的经济效益及社会效益等基本原则,可在满足各地区投资上下限条件下,按以下4种方法进行各地区间的投资分配。
4.2.1 按基本投资占比分配
基本投资反映各地区配电网基本建设需求,按各地区基本投资在总基本投资中的占比分配总投资有助于配电网的协调发展。在满足相应投资上下限条件下,各地区分配投资可由式(32)—式(34)求得。
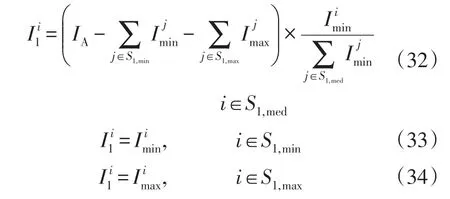
式中:为根据基本投资占比分配获得的第i地区的投资额;S1,min,S1,max和S1,med分别为按基本投资占比分配投资取下限、上限和上下限之间值的地区编号集合。
4.2.2 按等收益率分配
经济投资反映各地区配电网投资的经济合理性按相同经济收益率在各地区间分配总投资有助于平衡各地区配电网的经济收益。在满足相应投资上下限条件下,各地区分配投资可由式(35)—式(38)联立求解获得。

式中:为采用等收益率分配方法获得的第i地区的投资;S2,min,S2,max和S2,med分别为按等收益率分配投资取下限、上限和上下限之间值的地区编号集合。
4.2.3 按电量需求占比分配
电量反映各地区的社会需求,按各地区电量需求在总电量需求中的占比分配柔性总投资有助于平衡各地区电量需求。在满足相应投资上下限条件下,各地区分配投资可由式(39)—式(41)求得。
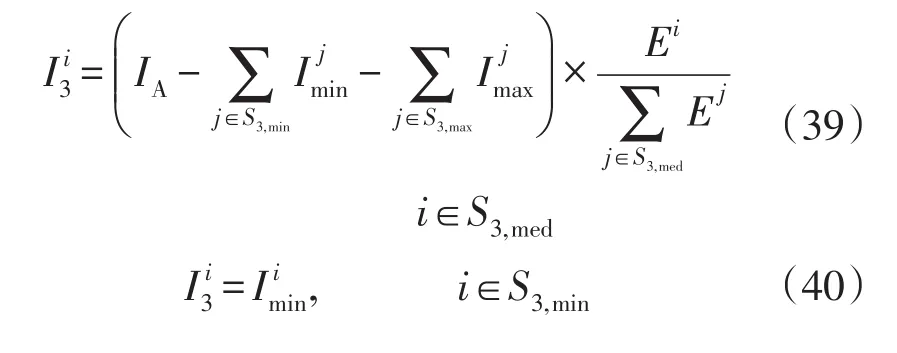
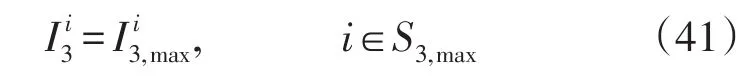
式中:为根据电量需求占比分配方法获得的第i地区的投资额;S3,min,S3,max和S3,med分别为按电量需求占比分配投资取下限、上限和上下限之间值的地区编号集合。
4.2.4 基于加权的综合分配
采用专家意见法对前3种分配方案的投资结果进行加权求和,以便综合考虑电网建设的基本需求以及投资的经济效益及社会效益。此时,第i地区的分配投资为

式中:为基于加权的综合分配方法获得的第i地区的投资额;ε1、ε2和ε3分别为对应3种方法的投资分配权重,可根据决策者经验引入人工干预。
5 总体思路和求解步骤
已知整个规划区域总投资,各地区投资分配决策的总体思路及求解步骤如下。
1)按配网现有规模和预测负荷估算各地区刚性投资。
2)按预测电量采用内部收益率法反算各地区配电网经济投资。
3)根据各地区刚性投资、经济投资和规划投资确定各地区分配投资的上下限。
4)基于上文投资分配模型策略,制定各地区投资分配方案,相应的流程步骤如图4所示。需要注意的是,各地区投资应考虑上下限约束,为此本文采用了启发式迭代方法。
①将上文计算公式中投资取下限和上限的地区编号集合初始化为空集,将投资取上下限之间值的地区编号集合初始化为含所有地区编号。
②采用上文的投资分配模型策略计算各地区投资。
③对于柔性总投资IF大于0的情况(即模型策略II),若在采用3种不同投资分配策略(即按基本投资占比分配、按等收益率分配和按电量需求占比分配)计算各地区投资过程中,没有发生某地区投资越限的情况,即获得了满足投资上下限约束的各地区投资分配方案;否则,继续到下一步。
④对于发生投资越限的地区,若越上限(或下限)则将其投资设置为相应投资上限(或下限),同时更新投资取上限、下限和上下限之间值的地区编号集合,返回步骤②。
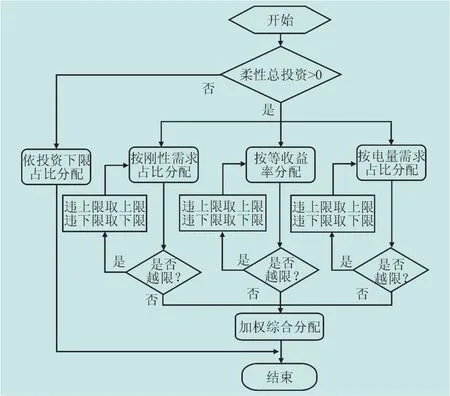
图4 配电网投资分配制定的流程步骤示意图Fig.4 Overall thinking lines and flowchart for investment allocation
6 实例计算分析
本文以隶属于Y省的15个市为研究对象,采用提出的模型及方法,分别对各市历史年及规划年配电网投资分配情况进行计算分析,通过对历史年(2017年)投资分配情况校验对规划年(2018年)的投资分配决策检测算法在实际配电网投资分配决策中的效果。
6.1 参数设置
本文算例采用的部分技术参数为:中压线路经济负载率0.45;配变经济负载率为0.6;中压负荷相对于配变负荷的同时系数为0.7;电网平均净收益电价为0.165元/(kW·h);设备使用年限为20 a;折旧维护率为3.5%;目标收益率为8%;电网建设投资占总投资比例为80%;电网建设中配网投资占比为55%。
6.2 历史年(2017年)投资分配计算分析
已知2017年Y省规划投资合计96.40亿元;实际投资合计56.87亿元。根据本文提出的模型和方法,计算得到Y省配电网总刚性投资55.30亿元,总经济投资109.10亿元,各市的各类投资情况分布如表2所示。

表2 2017年各地区各类型投资情况Tab.2 Investments of all the cities in 2017 亿元
采用本文提出的投资加权综合分配方法,在满足刚性需求的前提下,对各市配网投资进行分配,计算结果如图5所示。
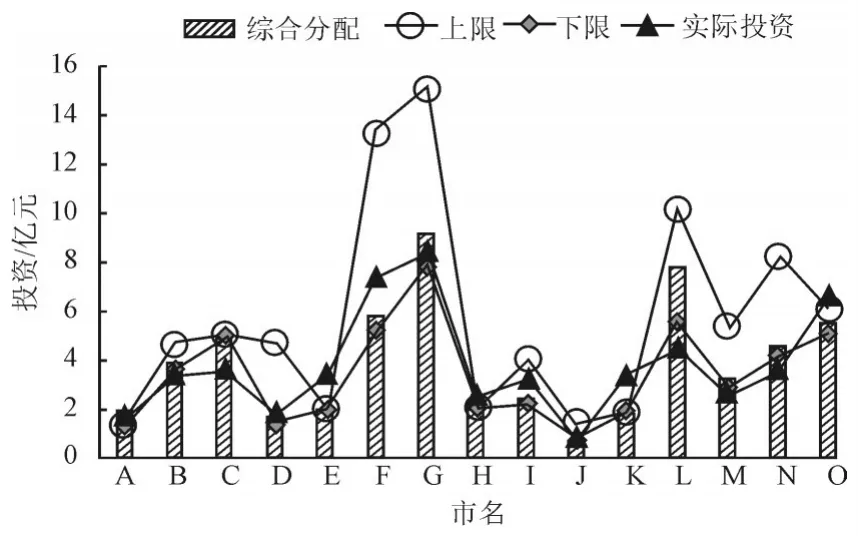
图5 2017年各地区投资分配结果Fig.5 Investments of all the cities in 2017
2017年大部分地区实际分配投资与理论计算投资趋势一致;其中B市、C市、G市、L市投资不足,A市、E市、F市、I市、K市、O市投资过胜;L市投资规划偏于保守,而省公司分配过程中未能得到有效倾斜,造成分配投资偏少;B市、C市、G市发展较快,配电网建设需求大,但实际分配投资比模型分配投资要少,这可能是造成这几个地方变电站重过载等指标较差的原因;A市新增负荷少,且新增电量小,在实际投资中应酌情减少投资。E市、F市、I市、K市新增负荷较少,配电网建设需求不大,但其规划投资较大,造成该地方投资过剩;虽然O市新增电量多,但O市现状电网带负载能力强,实际投资分配决策时应相对减少投资。
6.3 规划年(2018年)投资分配计算分析
已知2018年Y省规划总投资为83.85亿元。根据本文提出的模型和方法,计算得到Y省配电网总刚性投资56.75亿元,总经济投资120.09亿元,各市各类型投资分布结果如表3所示。

表3 2018年各地区各类型投资情况Tab.3 Investments of all the cities in 2018 unit:100 million Yuan
2018年Y省110 kV及以下配电网可分配总投资为62亿元。采用本文提出的投资加权综合分配方法,在满足刚性需求的前提下,对各市配网投资进行分配,结果如图6所示。

图6 2018年各地区投资分配结果Fig.6 Investments of all the cities in 2018
2018年规划投资普遍高于理论计算的分配投资。通过本文提出的模型计算后,部分经济及负荷发展较快的地区投资占比有所提高,如B市、C市和G市;部分前期投资过盛或负荷发展较缓慢的地区投资占比有所下降,如F市和K市。
投资分配结果在满足各地区负荷增长的同时,考虑到了其经济效益及社会效益,有利于配电网的平衡发展。
7 结论
1)提出了新的配电网投资分配模型策略,涉及刚性投资、柔性投资、经济投资和投资上限及下限的概念,为省市电力公司决策者对下级地区的投资分配提供更全面的决策信息。
2)推导了改造比例与设备使用年限和负荷增长率的关系表达式,为改造比例定量分析提供了参考依据。
3)考虑到配电网基本发展需要、投资的经济效益及社会效益等基本原则,提出了4种涉及柔性总投资的实用分配模型和方法,分别为按刚性需求占比分配、按等收益率分配、按电量需求占比分配和基于加权的综合分配。各地区分配到的柔性投资多少不会产生直接的收益,但有助于完善其配电网,提升其各项技术经济指标。
4)在中低压配电网新建投资估算中采用了目标负载率来衡量设备供电能力。目标负载率取值越大,投资越小;目标负载率一般采用经济负载率,也可基于不同接线模式采用其最大允许负载率。
5)可靠性、电压合格率和线损率等指标与目标负载率和供电半径关联性较强,在配电网规划中已经宏观规范了目标负载率和供电半径的合理值,但具体线路的负载率和供电半径还与规划及项目实施情况有关。因此,如存在某重要指标偏低的情况,可根据具体情况考虑相应的特殊刚性投资。
参考文献
[1]霍凯龙,王主丁,畅刚.目标年中压配电网规划实用方法[J].电网技术,2013(6):1769-1774.HUO Kailong, WANG Zhuding, CHANG Gang, A practical method for medium voltage distribution network planning in target year[J].Power System Technology,2013(6):1769-1774.
[2]朱文华,周星星.CEES电气计算软件在县级电网规划中的应用[J].电气技术,2014,15(11):73-76.ZHU Wenhua,ZHOU Xingxing.Application of the CEES to the planning for county power grids[J].Electrical Tech⁃nology,2014,15(11):73-76.
[3]孙可,那星,李欣,等.基于大数据的配电网规划智能辅助决策平台研究与应用[J].供用电,2016,33(11):31-35.SUN Ke,NA Xing,LI Xin,et al.Research and applica⁃tion of intelligent decision support system for distribution system planning based on big data[J].Distribution&Utili⁃zation,2016,33(11):31-35.
[4]陈雪,黄伟,叶琳浩,等.基于多源数据的配电网规划辅助决策系统研究[J].广东电力,2017,30(1):53-58.CHEN Xue,HUANG Wei,YE Linhao,et al.Auxiliary decision system for power distribution network planning based on multi-source data[J].Guangdong Electric Power,2017,30(1):53-58.
[5]王昌照.基于大数据的“三统一”配电网规划辅助决策系统[J].供用电,2017,34(1):32-37.WANG Changzhao.Big data based three-unified assistant decision-making system of distribution network planning[J].Distribution&Utilization,2017,34(1):32-37.
[6]方略,程浩忠,柳璐,等.基于多指标体系的10kV配电网投资分配评价[J].华东电力,2014,42(6):1092-1097.FANG Lüe,CHENG Haozhong,LIU Lu,et al.Evaluation of 10 kV distribution network investment allocation based on multi-index system[J].East China Electric Power,2014,42(6):1092-1097.
[7]崔文婷,刘洪,杨卫红,等.配电网投资分配及项目优选研究[J].中国电力,2015,48(11):149-154.CUI Wenting,LIU Hong,YANG Weihong,et al.Study on distribution network investment allocation and project selection optimization[J].China Electric Power,2015,48(11):149-154.
[8]张富强,罗慧,刘梅招,等.基于基尼系数的电力网络投资分配模型及应用[J].电力建设,2016,37(1):9-14.ZHANG Fuqiang,LUO Hui,LIU Meizhao,et al.A Gini coefficient based investment allocation model for power networks and its application[J].Electric Power Construc⁃tion,2016,37(1):9-14.
[9]崔巍,都秀文,杨海峰.供电公司投资规模模型研究[J].电力建设,2013,34(8):27-33.CUI Wei,DU Xiuwen,YANG Haifeng.Investment scale model of power supply company[J].Electric Power Con⁃struction,2013,34(8):27-33.
[10]杨卫红,王云飞,刘速飞,等.基于典型供电模式的配电网投资分配模型研究[J].电力设备,2016(14):109-114.YANG Weihong, WANGYunfei, LIU Sufei, etal.Research on distribution investment allocation model based on typical power supply mode[J].Electric Power Equipment,2016(14):109-114.
[11]朱永娟.基于地区发展的电网投资分配优化方法研究[J].电力与能源,2016(6):704-708.ZHU Yongjuan.Research on investment allocation optimi⁃zation model of power grid enterprises based on regional development[J].Electric Power and Energy,2016(6):704-708.

