考虑分布式电源出力随机性的配电网无功优化策略

余立武，李浩然，刘岩

（广东电网公司深圳供电局，广东深圳 518001）

分布式发电是布置在用户附近，与环境能够兼容、可独立地输出电能的系统[1-3]。目前大量不同类型的分布式电源并入配电网中[4]。

分布式电源目前主要分为出力稳定且可人工调整无功输出型DG和出力随机型DG（即不可控型分布式电源）两大类。前者可通过调整其控制参数结构调整DG的无功输出，后者受到气候、环境因素等自然因素的影响，其输出的功率会随机变化，主要包括光伏发电系统和变速恒频风力发电系统（doubly fed induction generator，DFIG）[5-6]。

文献[7]通过测试系统分析了DG对配电网络的节点电压分布和网损等方面的影响，为DG并网时的无功优化技术的探索在一定程度上提供了依据。文献[8]仅以网损为目标且通过模拟退火粒子群算法优化DG，实用性不强。文献[9]定性的分析了风电DG的无功功率及其范围对网络所带来的影响，缺乏对DG详细的控制方式的介绍。

SVG是一种既能发出感性无功又能发出容性无功的双向动态调节装置，具有反应迅速、谐波小、性价比高等一系列优点，在配电网中具有很好的发展前景[10]。

本文根据随机波动型分布式电源的出力特点，考虑其自身的无功补偿特性，研究了一种利用SVG动态无功补偿来维持随机波动型分布式电源节点电压稳定的控制策略，并对SVG容量的确定方式进行了详细说明。在此基础上，提出了含有出力随机型等不同类型的分布式电源的配电网的整体无功优化策略，利用一种改进的粒子群算法在MATLAB中对本文方法进行了实例仿真，通过对比分析，充分验证了本文所提出的方法的可行性和有效性。

1 改进粒子群算法在含分布式电源的配电网无功优化中的应用

基本粒子群算法在求解问题时操作简单、使用方便，但存在着严重的不足[11]，本文对基本粒子群算法进行如下两点改进。

1.1 粒子群位置的更新采用模糊控制

改进的粒子群更新迭代公式为

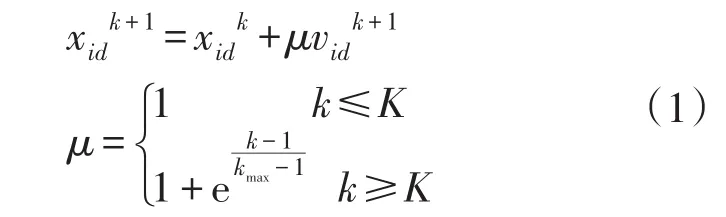
式中：xid，vid分别为每个粒子的飞行位置向量和速度向量；k为当前迭代次数；μ为S形隶属度函数；K为一给定阀值，与算法的最大迭代次数kmax相关。

在粒子群迭代初期时，隶属度μ取1，粒子群位置改变较大，节省粒子寻优的时间；当迭代次数大于给定的阀值K时，采用模糊控制，使粒子的位置缓慢变化，避免遗漏优良解，使粒子更加准确地接近最优解。

1.2 惯性权重ω的改进

为了使粒子群初始时飞行较快，在算法后期，粒子能够迅速准确地找到最优解，惯性权重ω采用如下式的非线性函数：

这里根据经验值取最小惯性权重ωmin为0.4，最大惯性权重ωmax为0.9。在算法初期，如k=1时，惯性权重ω为2ωmax-ωmin，取值较大，粒子的位置和速度更新较大，粒子群能够迅速靠近最优解，同时避免了陷入局部最优的危险；随着迭代次数的增加，惯性权重ω逐渐减小，并呈非线性变化，能够很好地适应粒子的寻优进度；当达到最大迭代次数时，惯性权重ω取值为最小值ωmin，算法趋于稳定，粒子缓慢更新，避免了粒子群遗漏优良解而跳出最优解的范围。

2 配电网无功优化数学模型

对于出力随机型等不同类型的分布式电源并网的无功优化，采取分段的方式，每一时段负荷取恒定值，考虑到电容器组调节次数的限制，每一段内，限定各调节设备只允许动作一次。采用的控制变量有连续量和离散量2种形式，其中，连续量包括出力稳定且功率可调型分布式电源的无功出力和SVG的动态无功输出，离散量包括并联电容器组的容量和变压器分接头位置。

数学模型采用考虑电压无功权重影响后的优化模型，目标函数和等式约束条件同文献[12]，不同之处在于DG并网后，相对于原有配电网中各个节点的电压约束、变压器分接头档位的约束和发电机的无功约束，还需要考虑可调出力的DG的无功限制，SVG连续可调的容量范围，出力随机波动型DG的无功出力极限，即：

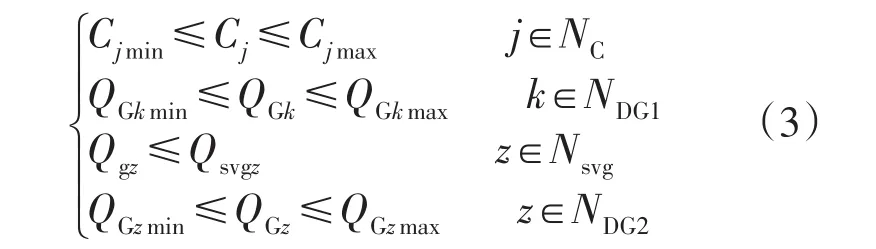
式中：NC，NDG1，Nsvg，NDG2分别为发电机节点、可调有载变压器节点、无功补偿节点、出力可调稳定型DG、随机波动型DG及SVG的集合；Cjmin，Cj，Cjmax分别为无功补偿点电容器组补偿容量的下限值、实际值和上限值；QGkmin，QGk，QGkmax为出力可调型DG无功输出的下限值、实际无功出力和无功输出的上限值；Qgz，Qsvgz为待确定的各个SVG的最小容量值及实际无功容量值；QGzmin，QGz，QGzmax为出力随机波动型DG向其并网点提供的无功出力的下限值、实际无功出力、无功出力的上限值，其中QGzmin为SVG的容性无功容量与每一分段内随机波动型DG的最小无功极限值Qzmin之和，即QGzmin=-Qsvgz+Qzmin，QGzmax为SVG的感性无功容量与每一分段内随机波动型DG的最大无功极限值Qzmax之和，即QGzmax=Qsvgz+Qzmax，这里，SVG以发出感性无功为正，且感性无功与容性无功容量的绝对值相等。

可见，由于DG的加入和SVG的作用，配电网无功优化的约束条件更加复杂。

3 配电网整体无功优化策略

3.1 SVG的容量确定

利用SVG的双向补偿性对随机型DG进行优化控制时，需要考虑SVG容量的选取，下面以双馈式风力发电机为例进行说明。

3.1.1 分段处理

将地区日负荷曲线和风速特性分成24个时间段，每一时段内负荷取恒定值，风速取平均预测风速，得到对应的DFIG的平均预测有功输出Pi和无功输出Qi，同时得到了理论上DFIG接入节点处的电压，并以此作为该时段内风机并网点电压的参考值UPCCref，如图1所示。其中，Pimax，Pimin为对应于Pi的有功输出的上限值和下限值。

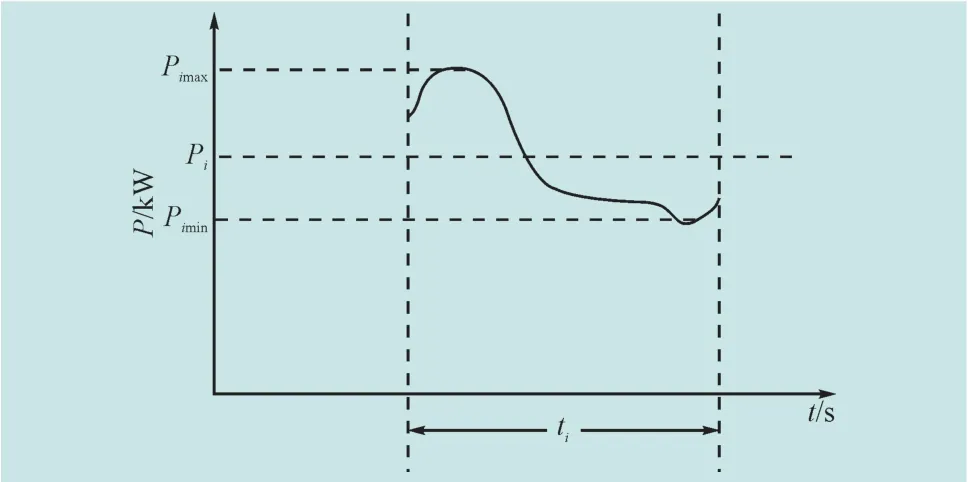
图1 DFIG的有功出力随时间变化曲线Fig.1 Active power output changing with time curve of DFIG

3.1.2 约束条件

在每一分段区间内，DFIG的有功出力和无功出力是随机变化的，通过并联一定容量的SVG动态跟踪电压参考值UPCCref使得DFIG仍然可作为PV节点处理，不同的是，DFIG的有功功率Pi不是定值，在无功优化时，要考虑其受限于其该分段内有功上限值Pimax和下限值Pimin之间，即满足约束条件Pimin＜Pi＜Pimax。

3.1.3 SVG最小容量

风速预测的误差及分段区间的不同使得SVG受其最小容量的限制。考虑到DFIG自身的功率特性和无功补偿容量[13]，对应于有功输出上限值Pimax，存在一个最大无功极限值和最小无功极限值，取二者绝对值的较大值，得到对应于Pimax的DFIG无功输出绝对值的极限值为Qi1max。同理得到对应于下限值Pimin的DFIG无功输出绝对值的极限值Qi2max。由于在此分段区间内，维持DFIG并网处的节点电压稳定在参考值UPCCref附近时，需要DFIG向其并网节点处补偿的平均无功功率为Qi，故SVG动态补偿的无功功率的最小值为

考虑所有分段后，得到DFIG并网时SVG的最小容量为

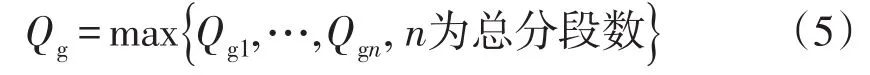
图1中，ti表示第i个分段区间，纵坐标P为双馈式风力发电机的有功出力值。

当配电网中无功不足时，不可能完全由SVG动态无功补偿，这里一定容量的SVG仅用于抑制DFIG并网所带来的随机波动，对整个配电网的无功优化需要进一步综合其他优化措施。

3.2 并联电容器组的补偿位置确定

传统的无功裕度法确定静态补偿装置的位置是基于传统的单向潮流放射状配电网络的，要求配电网能够稳定运行，节点电压和功率不会动态变化[14-17]。对于含有出力可调型DG和出力随机波动型DG的配电网络，需要对传统无功裕度法进行改进，其原理为：

1）SVG动态补偿后，每一段内DG并网点可相应作为特殊的PV、PI、PQ节点处理，首先按照传统无功裕度法计算出各个节点在分段区间ti内的等效无功裕度值，即

式中：Ni是与节点i相连的支路数；j是与节点i相连的节点编号；分别为对应节点的有功功率圆半径，无功功率圆半径及圆心距离D。

2）考虑所有分段区间后配电网中各个节点的平均等效无功裕度值为

式中：N为总的分段数；pti为分段区间ti在一天中出现的概率。

3）对平均等效无功裕度值进行排序，优先对较小的节点并联补偿电容器组。

3.3 基于改进粒子群算法的无功优化策略

不同类型的DG同时并网时，配电网络中的节点电压及功率大小分布会发生变化。按照本文的优化方法，首先，为稳定各个出力随机型DG并网点电压的稳定性，确定各个SVG的最小容量值，并确定SVG的安装位置，这里SVG的作用主要是用于抑制节点电压的波动和闪变，因此最小容量值不是很大，也满足经济性需要；然后根据改进无功裕度法确定配电网的并联的电容器组的安装位置；按照本文的数学模型采用改进粒子群算法进行无功优化计算后，根据所得的优化结果，当节点电压不满足要求，即节点电压的越上限和越下限时，优先调整出力可调型DG的无功输出，由于DG的功率输出一般在10 MW以下，这里无功调整的主要作用是用于对节点电压的大小进行微调，减弱配电网节点电压的升高和降低；在此基础上，综合考虑电压无功权重，按照本文的数学模型所得的优化结果，进一步投切一定容量的电容器组，并确定变压器分接头的位置。优化逻辑如图2所示。

图2 考虑分布式电源出力随机性的配电网无功优化逻辑框图Fig.2 Reactive power optimization logic diagram of the distribution network considering output randomness of DG

优化调整顺序如下：

1）根据理论分析值，确定SVG的安装位置及并网容量，以稳定随机型DG的电压。

2）利用改进无功裕度法确定电容器组的补偿位置。

3）节点电压不满足要求时，优先调整可调DG的无功，实现节点电压大小的微调。

4）根据改进粒子群算法优化结果，调整变压器分接头的位置和电容器组的投切容量，从而实现整个配电网最终的无功优化。

3.4 配电网无功优化的算法实现

改进后的粒子群算法在含有分布式电源的配电网无功优化中的实现步骤如下：

1）初始化。在主函数中随机选取一个规模为m的D维粒子种群，并随机初始化对应的初始位置向量和初始速度向量，其维数由控制变量数目决定。

如，Ti为有载可调变压器的变比，Ci为无功补偿装置的补偿容量。定义其他初始参数包括计算精度，最大迭代次数，粒子速度的上下限值向量，粒子位置的上下限值向量，控制变量步长以及含有分布式电源的配电网络的结构参数，这里配电网的网络潮流参数可单独放到M文件里作为子函数。

2）算法主要优化参数设置。确定更新迭代公式中的参数，包括学习因子，给定阈值K，最小惯性权重ωmin和最大惯性权重ωmax。

3）根据无功优化的目标函数，计算每个粒子的适应函数值。

4）比较粒子的个体适应函数值与局部最优值的适应值并进行替代更新。

5）比较粒子的个体适应函数值与全局最优值的适应值并进行替代更新。

6）根据迭代公式更新对应的xi和vi。

7）检查xi和vi是否在其的上下限值和之间，即确保粒子群满足不等的优化约束关系。

8）判断终止条件。

4 仿真验证

选取IEEE9节点数据进行实例仿真。原始配电网中包含3个电源节点，一个作为平衡节点，另外2个为传统的PV节点。其中，平衡节点的电压等级为16.5 kV，另外2个电源的电压等级分别为13.8 kV和18 kV。取各电源的平均额定电压为基准电压，各变压器的变比调节范围为0.9～1.1，上下调节档位数为±8。

未加入任何分布式电源时，按照IEEE9节点的标准数据，需要调节原电网各变压器分接头至1.1处，同时并联一定容量的电容器来维持整个配电网络的无功功率平衡。

现在向该配电网中并入不同类型的分布式电源，即在电压等级为13.8 kV的节点处并入双馈式分布式电源DFIG，在平衡节点处并入一功率双向输出型的蓄电池储能型分布式电源。

4.1 SVG的作用

并入分布式电源后，DFIG出口处节点电压的有效值的波形如图3所示。可见，此时DFIG并网点处的节点电压及其无功出力存在明显的波动性，DFIG并网运行时要吸收一定的无功功率，并且当风速达到最大值时，配电网出现了失稳的现象。利用SVG的动态补偿效果，DFIG在对应于3种风速下的无功功率极限值分别为0.057 MV·A，3.5 MV·A，3.5 MV·A，得到SVG的最小容量值约为4.56 MV·A，因此选取容量为5 MV·A的SVG并接到DFIG并网处变压器的低压侧，此时DFIG并网节点处电压的有效值波形如图4所示。

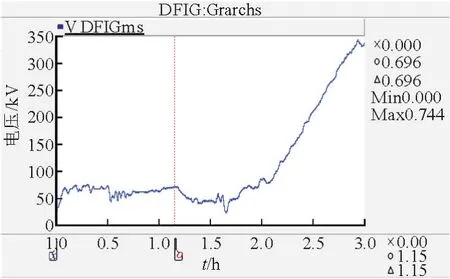
图3 未加入SVG时DFIG出口处电压有效值随时间变化的波形Fig.3 Voltage RMS changing with time curve of DFIG without SVG

图4 加入SVG后DFIG出口处电压有效值随时间变化的波形Fig.4 Voltage RMS changing with time curve of DFIG with SVG

对比图3和图4可知，利用一定容量的SVG对含有DFIG的配电网络进行无功补偿后，DFIG出口处节点电压基本不受风速随机波动的影响，能够很好的得到稳定，这样，在对整个配电系统进行无功优化时，即可将DFIG作为一特殊的PV节点来处理，很好的降低了DFIG的随机性所带来的影响。

4.2 改进粒子群算法的综合优化结果

对整个配电网进行无功优化，即：

1）首先对整个负荷曲线进行分段，为说明仿真效果，这里取其中的典型负荷段的负荷的情况进行说明，即节点5、节点7、节点8和节点9处的负荷值分别为P5=90 MW，Q5=40 MV·A，P7=100 MW，Q7=55 MV·A，P8=35 MW，Q8=10 MV·A，P9=125 MW，Q9=70 MV·A。

2）用改进无功裕度法对各节点静态无功裕度从小到大进行排序，可选取稳定裕度较低的5，7，9节点进行补偿或者5，9两点进行补偿。比较得到，在5，9两个节点进行补偿时各节点电压均在上下限值之间，但电压偏移量较大，网损量也较大（补偿3个节点时为 12.298 MW，补偿2个节点时为12.479 MW），不如在5，7，9三个节点补偿的情况，因此在条件允许的情况下，选取补偿电压稳定裕度相对较小5，7，9三个节点。

3）利用SVG动态补偿后，电网的节点电压虽然满足稳定要求，但是此时各变压器高压侧的电压值仍然均低于额定值下限值，首先调节变压器分接头至1.1处，调节后各节点电压值基本稳定在额定值附近，但节点5，6，9的电压仍低于额定值，如6节点电压为0.949 5，接近电压下限值0.95。

4）此时出力双向可调的储能型分布式电源CELL是吸收功率（作为负荷）的，即Q=-13.44 MV·A。调节CELL的输出功率值，至P=-10.43MW，Q=3.527MW时，储能型分布式电源已经作为无功电源，但是其补偿的无功功率相对于系统电源提供的无功功率仍然很小，节点6的电压仍接近于电压下限值，由于CELL功率一般为10 MW级以下，渗透率较低，调节不能满足要求，此时需考虑进一步通过静态无功补偿装置对整个配电网优化。

5）综合考虑整个配电网的有功网损和电压无功权重，利用改进粒子群算法，对整个配电网进行无功优化，即确定相应节点处并联电容器组的补偿容量大小。优化前和优化后，配电网的节点电压和网络损耗对比如附录中表1所示。

由表1可知，优化前，若干节点电压值低于额定运行下限值，优化后，需在节点5处补偿0-50=-50 MV·A，节点 7处补偿 5-55=-50 MV·A，9节点处补偿20-70=-50 MV·A，负号代表补偿无功功率。补偿后，配电网中各个节点的电压和网损均得到了明显的改善，为了对比说明，增大节点的负荷值，取另一段分段区间内负荷处于高峰时进行优化。即，P5=200 MW，Q5=100 MV·A，P7=100 MW，Q7=55 MV·A，P8=100 MW，Q8=50 MV·A，P9=105 MW，Q9=70 MV·A。得到利用基本粒子群算法和改进粒子群算法优化前后，配电网的节点电压和网络损耗的对比表如表1、表2所示。

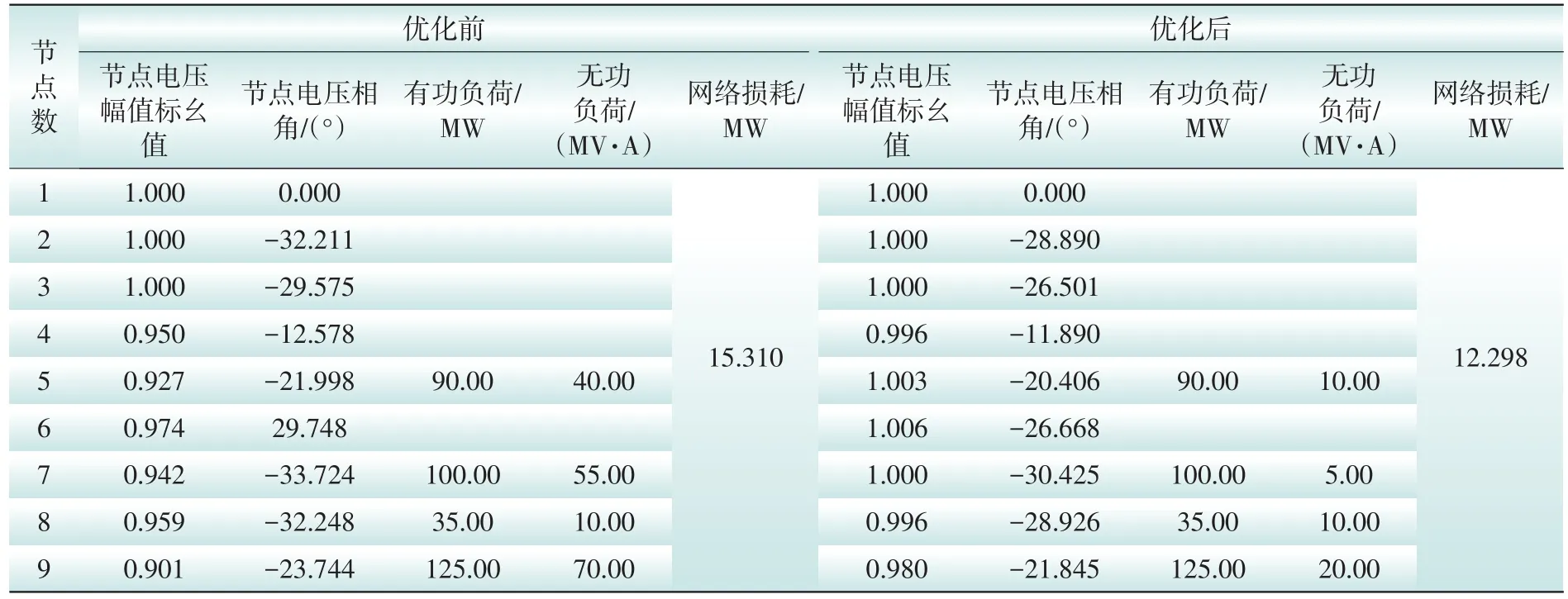
表1 改进粒子群算法优化前后配电网的节点电压和网络损耗对比表Tab.1 Comparison chart of distribution network node voltage and power loss before and after optimization with improved particle swarm algorithm

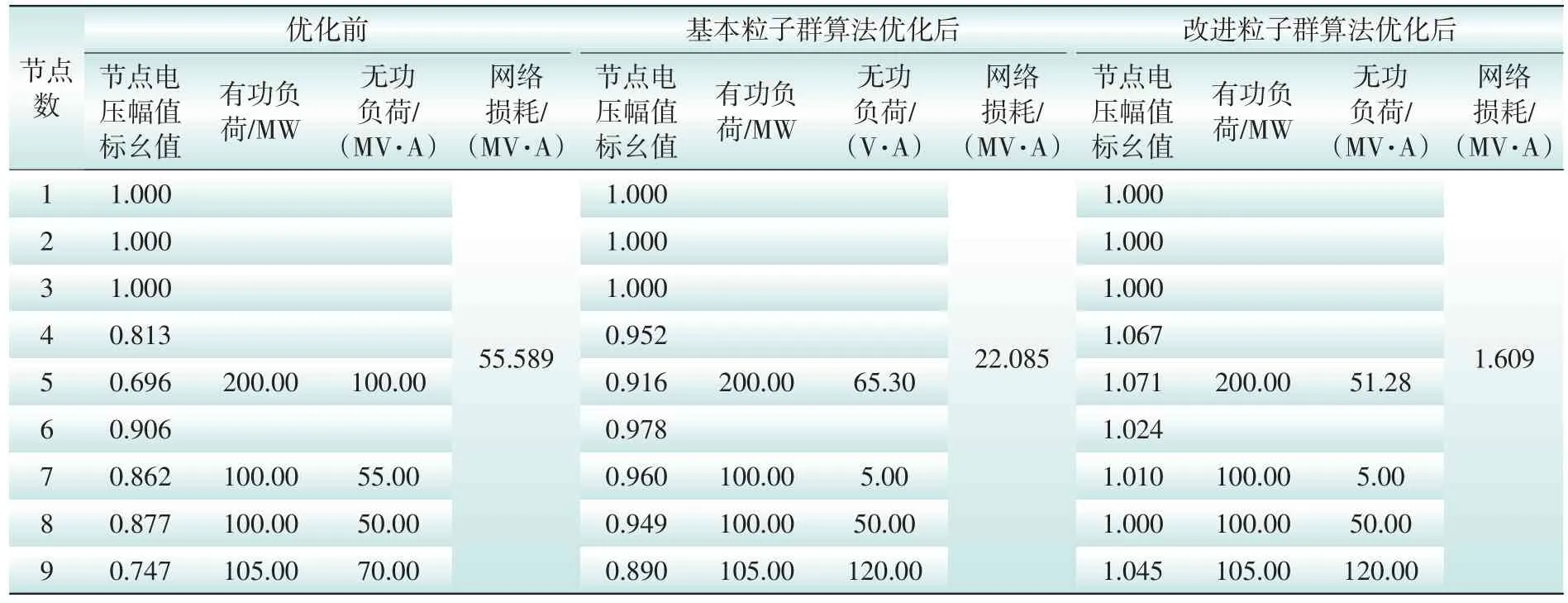
表2 高峰负荷段优化前后配电网的节点电压和网络损耗对比表Tab.2 Comparison chart of distribution network node voltage and power loss before and after optimization in peak load period

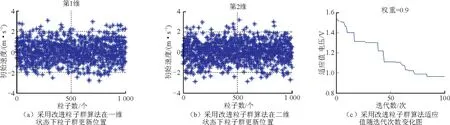
图5 采用基本粒子群算法时粒子群更新位置及适应值随迭代次数的变化图Fig.5 Location updating state and adapt value vs.number of iterations using basic particle swarm algorithm

另外，负荷高峰时，采用基本粒子群算法优化时，粒子群在迭代85次左右时才趋于稳定，采用本文改进的粒子群算法优化时，在迭代15次左右的时候已经趋于稳定。如图5和图6所示。

因此，结合图5图6及表2可知，当配电网处于负荷高峰期时，优化补偿前，配电网中的节点电压明显偏离额定值，严重超过配电网节点额定电压的上下限值，且存在较大的网络损耗，利用基本粒子群算法优化时很不稳定，耗时长，且优化效果不佳。而采用本文的改进粒子群算法对配电网络进行无功优化补偿后，配电网的节点电压得到明显改善，网络损耗也较小，且能够更加迅速可靠地找到最优解，明显提高了优化的效率和效果，充分显示了本文方法的优越性。

图6 采用改进粒子群算法时粒子群更新位置及适应值随迭代次数的变化图Fig.6 Location updating state and adapt value vs.number of iterations using improved particle swarm algorithm

5 结语

本文针对出力随机波动型的分布式电源并网时带来的电压波动闪变的影响，提出了一种利用一定容量的SVG来维持节点电压的稳定的控制策略，并详细分析了SVG最小容量的确定方法。在此基础上，研究并提出了考虑分布式电源出力随机性的配电网的整体无功优化策略。

利用IEEE9节点配电网进行实例仿真，验证了SVG在配电网无功电压中应用的可行性，在MATLAB中通过利用改进的粒子群算法对整个配电网络进行综合无功优化，凸显了本文所采用的模糊控制的改进粒子群方法的优化效果，充分验证了本文所提出的优化策略的可行性和有效性。

本文研究对工程应用具有很好借鉴和指导意义，由于个人时间有限，对高渗透率分布式电源并时，所带来的无功优化问题有待深入探讨。

参考文献

[1]梁振锋，杨晓萍，张娉.分布式发电技术及其在中国的发展[J].西北水电，2006，10（1）：51-53.LIANG Zhenfeng，YANG Xiaoping，ZHANG Ping.Dis⁃tributed power generation technology and its development in China[J].Northwest Hydro Power，2006，10（1）：51-53.

[2]冯希科.考虑分布式发电的配电网保护方案研究[D].上海：上海交通大学，2010.

[3]贺海，吕娟，王磊.改进粒子群算法在分布式电源优化配置中的应用研究[J].电力科学与工程，2013，29（2）：21-25.HE Hai，LÜ Juan，WANG Lei.Applied research on dis⁃tributed generation optimal allocation based on improved particle swarm optimization algorithm[J].Electric Power Science and Engineering，2013，29（2）：21-25.

[4]王志群，朱守真，周双喜，等.分布式发电对配电网电压分布的影响[J].电力系统自动化，2004，28（16）：56-60.WANG Zhiqun，ZHU Shouzhen，ZHOU Shuangxi，et al.Impacts of distributed genetatuin on distribution system voltage profile[J].Automation of Electric Power Sys⁃tems，2004，28（16）：56-60.

[5]魏希文，邱晓燕，李兴源，等.含风电场的电网多目标无功优化[J].电力系统保护与控制，2010，38（17）：107-111.WEI Xiwen，QIU Xiaoyan，LI Xingyuan，et al.Multiobjective reactive power optimization in power system with wind farm[J].Power System Protection and Control，2010，38（17）：107-111.

[6]陈海焱，陈金富，段献忠，等.含风电机组的配网无功优化[J].中国电机工程学报，2008，28（7）：40-45.CHEN Haiyan，CHEN Jinfu，DUAN Xianzhong，et al.Re⁃active power optimization in distribution system with wind power generators[J].Proceedings of the CSEE，2008，28（7）：40-45.

[7]BORGES C L T，FALCAO D M.Impact of distributed gen⁃eration allocation and sizing on reliability，losses and volt⁃age profile[C]//Power Tech Conference Proceedings，June，2003，5.

[8]王旭强，刘广一，曾沅，等.分布式电源接入下配电网电压无功控制效果分析[J].电力系统保护与控制，2014，42（1）：47-53.WANG Xuqiang，LIU Guangyi，ZENG Yuan， et al.Analysison the effectsofVolt/Varcontrolmethod considering distributed generation[J].Power System Protection and Control，2014，42（1）：47-53.

[9]TIAN Xinshou，LI Gengyin，CHI Yongning，et al.Voltage phase angle jump characteristic of DFIGs in case of weak grid connection and grid fault[J].Journal of Modern Power Systems and Clean Energy，2016，4（2）：256-264.

[10]徐惠勇.无功功率补偿中SVG技术的研究现状与发展[J].应用能源技术，2012（4）：31-33.XU Huiyong.Reactive power compensation in SVG tech⁃nology research present situation and the development[J].Applied Energy Technology，2012（4）：31-33.

[11]刘传铨，张焰.电力系统无功补偿点及其补偿容量的确定[J].电网技术，2007，31（12）：78-81.LIU Chuanquan，ZHANG Yan.Confirmation of reactive power compensation node and its optimal compensation capacity[J].Power System Technology，2007，31（12）：78-81.

[12]王世丹.含分布式电源的配电系统无功优化技术研究[D].北京：北京交通大学，2012.

[13]申洪，王伟胜，戴慧珠.变速恒频风力发电机组的无功功率极限[J].电网技术，2003，27（11）：61-62.SHEN Hong，WANG Weisheng，DAI Huizhu.Reactive power limit of variable-speed constant-frequency wind turbine[J].Power System Technology，2003，27（11）：61-62.

[14]江明水.基于粒子群优化算法的地区电网电压无功控制的研究[D].保定：华北电力大学，2005.

[15]余乐，张茜，刘燕，等.含分布式电源的配电网无功补偿分区平衡优化调节方法[J].电力系统保护与控制，2017，45（5）：58-64.YU Le，ZHANG Xi，LIU Yan，et al.An adjustment meth⁃od of distribution network reactive power compensation partition balance with distributed power sources[J].Power System Protection and Control，2017，45（5）：58-64.

[16]迟永宁，田新首，汤海雁，等.双馈风电机组与静止无功发生器交互作用原理及系统振荡特性研究[J].电网技术，2017（2）：486-492.CHI Yongning，TIAN Xinshou，TANG Haiyan，et al.Interactions between DFIGs and SVG and oscillation characteristics of power grid connected wind turbines[J].Power System Technology，2017（2）：486-492.

[17]董萍，徐良德，刘明波，等.大电网多站点无功补偿协调控制的多目标混合优化方法[J].电工技术学报，2017，32（2）：271-274.DONG Ping，XU Liangde，LIU Mingbo，et al.Multiobjective hybrid optimization method for coordinated contro l of reactivepower compensation devices among multiple su bstations in large-scale power systems[J].Transactions of China Electrotechnical Society，2017，32（2）：271-274.