一种新颖的电力系统级联故障风险评估方法设计

宋永强，王杰，潘亮亮，金海川

（国家电网宁夏电力公司吴忠供电公司，宁夏吴忠 751100）

电网互联可以提高系统的运行效率，获得更大的经济效益，但也增加了运营的不确定性，使得系统动态行为更加复杂，并将本地电网故障的影响扩大到附近的区域电网。这更可能导致由级联故障引起的停电[1]，而相关人员已经进行了诸多研究来确定这种事件的原因[2-9]。

由于受内部系统和外部环境的影响，电力系统的故障概率在实际系统中具有时变特性，故障概率模型难以确定[10]。由于缺乏统计样本和长期的统计数据，难以建立评估模型。电力系统部件（如输电线路，变压器和发电机）的严重性指数即系统突发事件的严重性，用于量化系统突发事件的严重程度。当系统处于正常工作状态之外时，其不能够代表系统当前的安全程度以及不安全的“距离”。严重性指数主要通过将系统中的每个严重性进行加权来形成，还可以根据不同的重点，以主观假设来选择权重系数。

基于不确定性理论，本文将系统级联故障视为不确定事件，提出了一种采用可信性度量的风险评估方法，建立了组件故障概率和全局模糊安全指标，用于测量事故严重程度。隐藏故障模型用于描述系统级联故障的演进机制。此外，将N-K意外事件作为系统级联故障的校准标准，通过计算故障风险指数来评估灾难性事件。采用RSTS六总线系统对所提方法进行验证，与传统风险评估方法的比较表明，所提出的方法是正确合理的。

1 电力系统级联故障风险指数

1.1 不确定性理论

1933年，数学家kolmogoroy[11]通过经典测量理论提出了3个公理，建立了全概率理论的公理系统。由于经典集合论和概率论不适用于模糊从属集，zadeh提出了模糊集的概念，并引入了可能性测度和必要性测度。虽然可能性测度和必要性测度是对偶的，但其均没有自对偶性[12]。理论上与实际应用中，自对偶测度更为必要，故刘宝碇教授在2004年提出了一个满足自对偶的sugeno模糊测度—可信性理论。

以模糊性为例，可信性测度定义如下：

假设Θ是非空集合，P（Θ）是Θ的幂集，Pos（A）是A的可能性测度，（Θ，P（Θ），Pos）是可能性空间。对于任何元素A∈Р（Θ），Ac为A的互补集，Nec（A）为A的必要性测度，满足

Cr（A）定义为A的可信性测度

显然，可信度 Cr（A）是以可能性测度 Pos（A）为基础的。跟可能性测度相比之下，其具有自对偶性：

1.2 电力系统级联故障可能性指标

假设线路d连接到线路l。当线路l跳闸时，流过线d（d=1，2，...，n）的电流Id作为模糊变量。因此，线路的隐藏故障可信性测度：

这里选择较大的运营商；s是线路d的运行状态；B和Bc分别代表线路跳闸和正常工作；μ是Id的隶属函数。

根据可能性概率一致性原理[13]，本文采用的方法如下：

式中：f（Id）表示由概率分布函数P（Id）所确定的线d的隐藏故障概率密度函数[14]。将P（Id）代入式（5），可以得到：

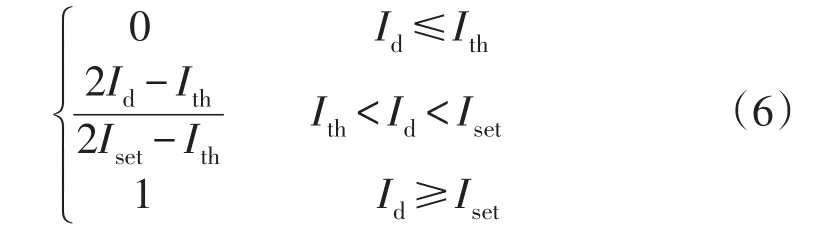
式中：Iset表示线路的过流继电器设置；Ith表示线路隐藏故障发生的阈值。根据式（6）可知，μ只与Iset和Ith相关。

1.3 电力系统级联故障严重性指数

电力系统运行状态的特征在于线路功率流，总线电压和发电机的有功/无功负载[15]。本文提出了5种严重性指标，即线路过载、总线高电压、总线低电压、发电机的有功功率余量和无功功率余量。严重性指标如下

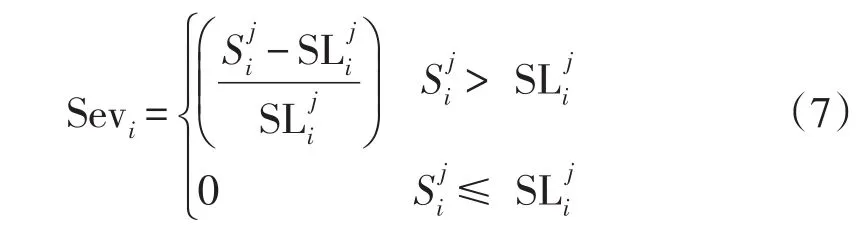
式中：Sevi（i=1～5）表示i型的严重度指标值；、分别是与系统状态变量相对应的i型严重性指标以及系统状态变量的限度。

对于系统中的任何组件，其抗干扰能力不是固定点值，而是[Tlow，Tup]区域的范围。当扰动低于Tlow时，系统能够正常工作；当干扰超过Tup时，系统处于不安全状态；当系统扰动在Tlow和Tup之间时，系统的安全状态具有不确定性。为了表征这种不确定性，本文基于模糊推理建立与各种严重性指标对应的隶属函数μsev，并通过计算最小隶属度μpss，得到系统的全局模糊安全指数GFSI[15]和GFSI′。

对于每个指标，随着事故严重程度的增加，指标值呈现出单调的增长趋势。系统安全性也相应降低[16]。μsev随着Sev的变化而呈线性变化，如图1所示。

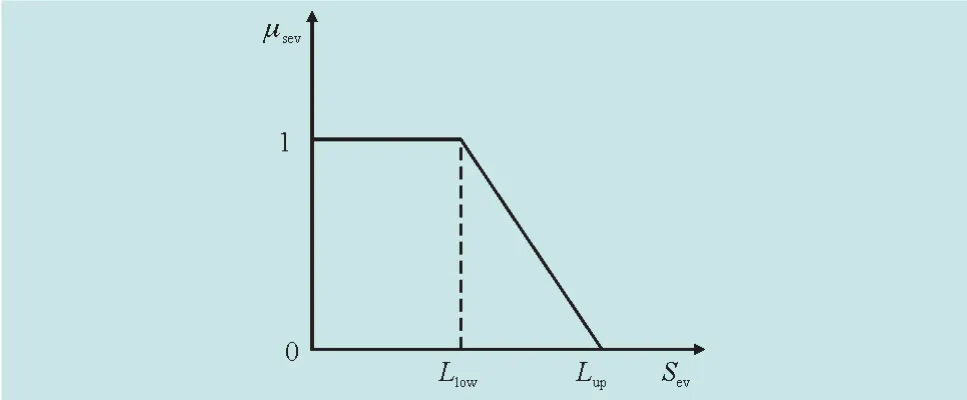
图1 各个严重性指标相对于电力系统安全性的隶属函数Fig.1 The membership function of each severity index relative to the power system security

对应于 Sev1～Sev5的 5 种类型，文中假设（Llow，Lup）分别为（0.01，0.09）、（0.002 5，0.01）、（0.002 5，0.01）、（0.004 9，0.022 5）、（0.004 9，0.022 5）。

系统组件可分为3种类型，即线路、总线和发电机。线路对应于Sev1，总线对应于Sev2和Sev3；发电机对应于Sev4和Sev5。对于系统给定的操作条件，对应于Sevi的最小隶属度由下式给出

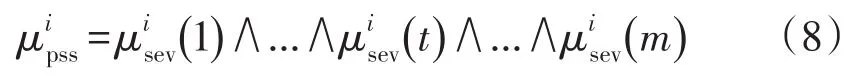
式中：t表示相对应于Sevi的第t个电器元件组件；模糊运算符∧意味着得到较小的。

因此，对应于不同类型组件的最小隶属度和GRSI由下式给出：

式中：分别表示线路、总线和发电机的最小隶属度。同样，用μ′sev代替μsev，系统非安全隶属函数对应于严重性指标，有：

以类似的方式，可以获得另一种类型的全局模糊安全指数GFSI′：

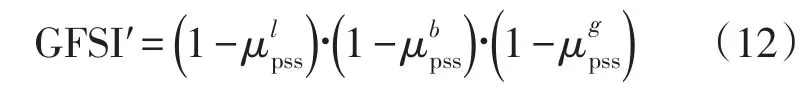
GFSI和GFSI′考虑到线路、总线和发电机的综合影响，其反映了安全和不安全的2个方面，系统当前运行状态与不安全运行之间的距离。

1.4 电力系统级联故障风险指数

风险指数是可能性和故障严重程度的结合物。结合式（4）和式（12），系统运行风险指数如下

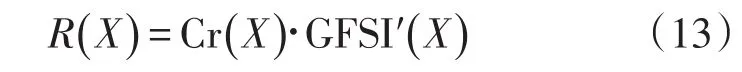
式中：X和R（X）分别代表当前运行状态及其风险指数。

2 系统级联故障评估模型

在电力系统中，由于缺乏无功功率而导致的动态不稳定性和电压崩溃引起的大量负载脱落是导致一系列电气部件（发电机或分支）级联跳闸的主要原因，这可能导致系统发生灾难性事件[14]。完整的灾难性事件序列数据库可以通过离线分析存储，以便在线评估系统的任何运行状况。因此，有必要采取相应的预防和正确的控制措施，保证电力系统安全稳定运行。灾难性事件序列也称为崩溃序列（CS），其被定义为系统从正常运行状态向灾难性事件状态演化期间的一系列元件故障序列。例如，当由于线路、变压器或发电机的级联跳闸而发生灾难性事件时，CS表示如下[14]

式中：L、T和G分别表示线路、变压器和发电机。

将N-k个偶然事件作为系统级联故障的校准原则，用于系统风险评估。当某些组件停止运行时，与其连接的其他组件可能由于隐藏的故障而发生故障。模拟仿真以N-1个偶然事件作为级联故障的初始事件，对每个模拟层的每个事件风险指数进行排列，并选择顶部q组的偶然事件作为下一个模拟层的初始化事件。当负载流量偏差或负载损耗＞20%时，定义为灾难性事件[17]。

为了简化计算，本文做出以下假设：1）假设系统中有足够的无功功率储备，线路故障的可能性远大于几台发电机的同时故障，基于电压的隐藏故障被忽略；2）多线路保护隐藏故障的概率远小于单一隐藏故障的概率[14]。若任何传输线路跳闸，则连接到同一总线的所有线路中最多只有一条线路将不正确地跳闸。

根据上述评估模式和原则，评估程序步骤如下：

1）获取模拟参数，并设置Layer=1；

2）若Layer=1，则执行N-1个偶然事件，否则搜索可能导致隐藏故障的组件序列；

3）指定Number，模拟故障的序列号，并设置h=1；

4）计算功率流量，若负载流量偏差或负载损耗大于20%，则将其作为崩溃序列保存；

5）计算 Cr、GFSI′和 R，设h=h+1；

6）若h＞Number，根据风险指数进行排序，存储q组风险突发事件，并设置Layer=Layer+1；反之，转到步骤4）；

7）若 Layer＜Max_Layer，则转到步骤 2）；否则，模拟测试完成。

3 模拟结果与讨论

本文使用RSTS六总线系统[18]作为测试系统。如图2所示，测试系统包括6条总线，9条传输线和2台发电机。由于缺乏与系统实际运行条件相比较的标准，系统上的事故严重程度可通过f（最小隶属度=0）的数量来确定。f数量越多，则对系统安全性的影响越严重。

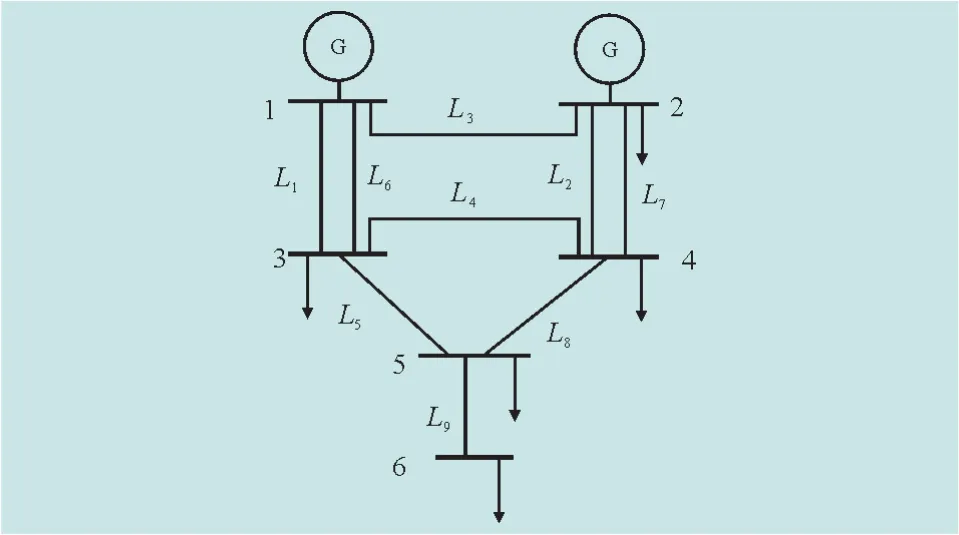
图2 RSTS六总线系统Fig.2 RSTS six bus system

3.1 所有N-1事故的风险排序

选择N-1个偶然事件作为级联故障和风险排序的初始事件，风险排序的方式对下一个模拟层有较大的影响。本文提出的方法根据f的数量，确定N-1个偶然事件的风险排序。然而，传统的风险评估方法对严重性指数进行加权平均来描述事件的严重性。严重性指数（Sev）如式（15）所示，加权系数如表1所示。

表1 传统风险评估方法加权参数Tab.1 Weighted parameters of the traditional risk assessment method

式中：W1～W5对应于 Sev1～Sev5的权重系数；h是与Sevi对应的电子部件的第h个子组件。

所有N-1事故的风险排名，如表2所示。由表2可知，N-1个偶然事件的风险排序根据本文提出的方法可由f的数量分为3个层次。

当一些线路跳闸时，负载流量的重新分配将导致系统具有不同类型的风险。线路L1，L2，L3，L6，L7和L8的跳闸将具有导致线路过载的高风险，以及系统中有功功率余量和无功功率裕度的高风险。线路L9的跳闸会导致系统线路过载的高风险，以及系统总线电压低和有功功率裕量的高风险。线路L5的跳闸将导致系统中总线电压低以及总线电压高的高风险。线路L4的跳闸只会导致系统无功功率裕度的高风险。结合实际经验，线路L1，L2，L3，L6，L7，L8，L9的跳闸将对整个系统造成最严重的潜在风险。而线路L4的跳闸对系统影响较小，线路L5的跳闸对系统的影响在上述两者之间。通过上述分析可以得出结论，本文提出方法的仿真结果更符合实际的电力系统运行状态。风险评估系数的严重程度是根据传统方法1和方法2的经验与主观假设，其结果导致不同的结论，与实际经验有较大偏差。

表2 所有N-1事故风险排序Tab.2 Sequencing of all N-1 accident risks

3.2 折叠序列的评估

表3显示了使用不同方法（包括本文提出的方法，传统方法1和2）所得到的折叠序列，并在表4中给出了不同方法的比较结果。比较1和比较2分别表示本文提出的方法与传统方法1和2之间的相对误差，比较3表示传统方法1和2之间的相对误差。相对误差可以表示如下：

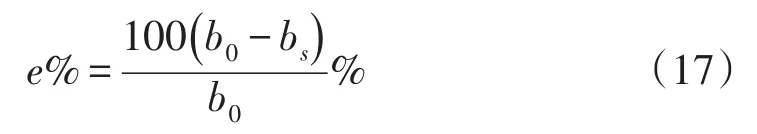
式中：b0是使用传统方法的折叠序列数；bs是使用不同方法的相同折叠序列的数量。

根据表3可知，当模拟层数为2～4时，本文提出的方法与传统方法1和方法2的最大相对误差为40%。由于上层风险事件作为下一个模拟层的起始事件，因此在每个模拟层期间，下一个模拟层的折叠序列受上层模拟层的影响，并直接影响折叠序列的最终结果。因此，与传统方法1和2相比，本文提出的方法发生较大的相对误差。然而，本文所提出的方法是基于整体系统而不是主观假设的。而传统方法1和2的严重性指数的权重系数是以主观和假设为前提根据不同的焦点选择的，不同的权重系数导致不同的评估结果。根据比较3，方法1与方法2的最大相对误差为60.00%。因此，本文所提出的方法更符合实际电力系统的运行状态，且具有更好的实用性和有效性。

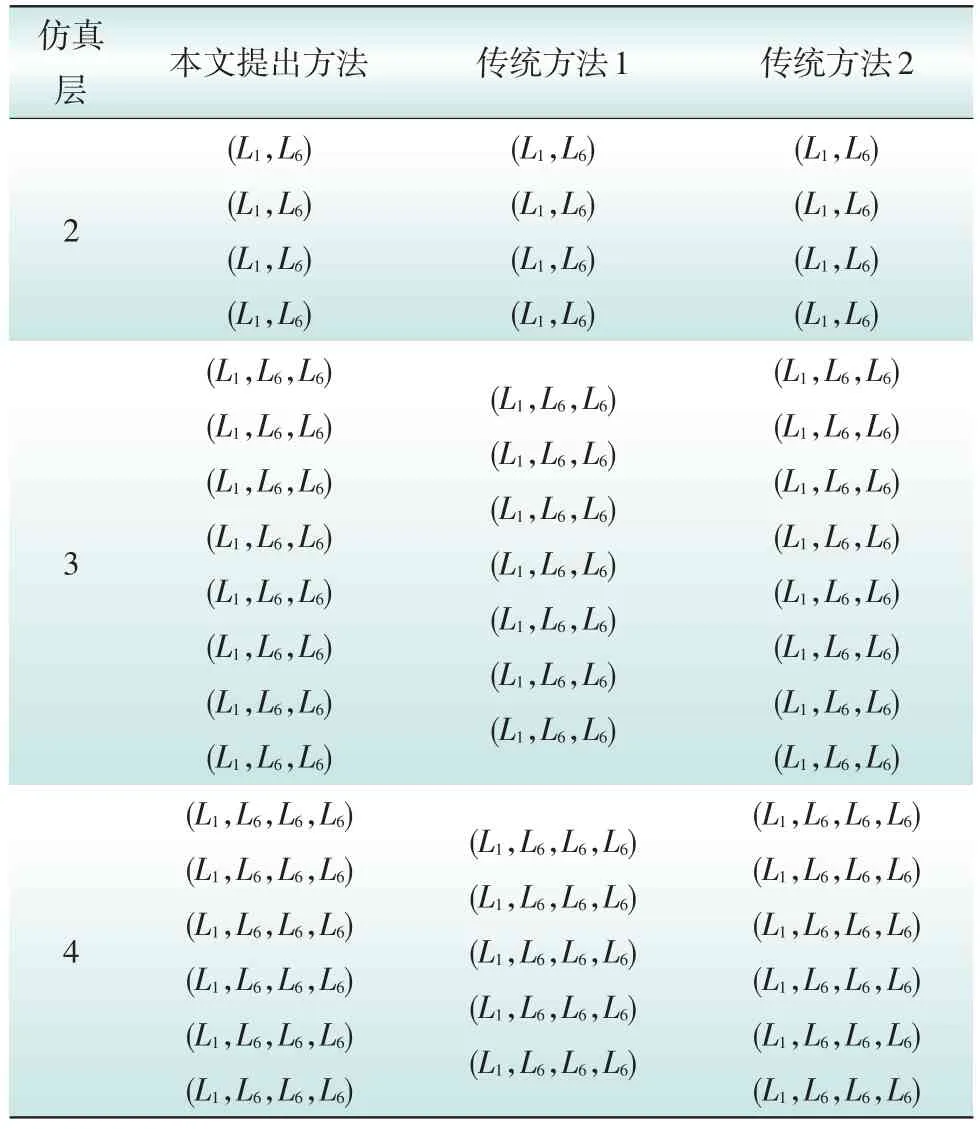
表3 不同方法的折叠序列Tab.3 Folding sequences of different methods

表4 比较1和2的相对误差Tab.4 Comparison of relative errors of 1 and 2

4 结语

基于不确定性理论，本文提出了一种电力系统中级联故障所导致的灾难性事件的可能序列模型。这些灾难性事件序列通过采用风险指标和不确定性理论，可以更合理地描述灾难性事件的不确定性规则。考虑到传统风险评估方法中事件发生概率和严重度的不足，本文基于可信性测度和全局模糊安全指数建立风险指标。同时，对文中所提出的方法进行了系统仿真验证，并与传统风险评估方法进行了比较。测试结果证明，基于不确定性理论的评估方法更适合实际系统。此外，如何构建实际电力系统灾难性事件的一系列在线识别系统，以及如何在实际工程中普及应用，将是下一步的研究重点。

参考文献

[1]WANG Meiyi，WU Jingchang，MENG Dingzhong.Large power system techniques[C].Beijng，China：China Elec⁃tric Power Press，2011.

[2]GAN Deqiang，HU Jiangyi，HAN Zhenxiang.Thoughts on several blackouts in the world in 2013[J].Automation of Electric Power Systems，2014，28（3）：1-5.

[3]HAN Zhenxiang，CAO Yijia.Power system security and its prevention[J].PowerSystemTechnology，2014，28（9）：1-6.

[4]白宪庆，刘劭玮，李宝昕.自动重合闸重合于永久性故障对电力系统暂态稳定的影响[J].电网与清洁能源，2015（7）：69-73.BAI Xianqing，LIU Shaowei，LI Baoxin.Influence of re⁃closing on permanent faults on power system transient sta⁃bility[J].Power System and Clean Energy，2015（7）：69-73.

[5]SUN Ke，HAN Zhenxiang，CAO Yijia.Review on models of cascading failure in complex power grid[J].Power Sys⁃tem Technology，2015，29（13）：1-9.

[6]曹炜，徐永海，李善颖，等.适用于大容量储能系统的级联H桥和模块化多电平逆变器分析比较[J].电网与清洁能源，2016，32（4）：30-37.CAO Wei，XU Yonghai，LI Shanying，et al.Analysis and comparison of cascaded H bridges and modular multilevel inverters for large capacity energy storage systems[J].Po⁃wer System and Clean Energy，2016，32（4）：30-37.

[7]DOBSON I，CARRERAS B A，LYNCH V E，et al.An ini⁃tial model for complex dynamics in electric power system blackouts[C]//Hawaii：Proceedings of the 34th Annual Ha⁃waii International Conference on System Sciences，2011.

[8]方丽华，熊小伏，方嵩，等.基于电网故障与气象因果关联分析的系统风险控制决策[J].电力系统保护与控制，2014（17）：113-119.FANG Lihua，XIONG Xiao Fu，FANG Song，et al.Sys⁃tem risk control decision based on causality analysis of power grid fault and weather[J].Power System Protection and Control，2014（17）：113-119.

[9]唐斐，陆于平.分布式发电系统故障定位新算法[J].电力系统保护与控制，2010，38（20）：62-68.TANG Fei，LU Yuping.A new algorithm for fault location in distributed generation systems[J].Power System Protec⁃tion and Control，2010，38（20）：62-68.

[10]NING Liaoyi，WU Wenchuan，ZHANG Boming，et al.Component outage modeling method for operation risk as⁃sessment with limited power component’s failure data[J].Proceeding of the CSEE，2009，29（25）：26-31.

[12]LIU Baoding，PENG Jin.A course in uncertainty theory[C].Bejing，China：Tsinghua University Press，2015.

[13]BAODING Liu.A survey of credibility theory[J].Fuzzy Op⁃timization and Decision Making，2016，5（4）：387-408.

[14]LIMA B S L P，TEIXEIRA E C，EBECKEN N F F.Proba⁃bilistic and possibilistic method for the elastoplastic analy⁃sis of soils[J].Advances in Engineering Software，2011，32（7）：569-585.

[15]曹积欣，王冠军，李建民.风电并网电力系统无功补偿动态性能研究[J].电力电容器与无功补偿，2012，33（3）：16-22.CAO Jixin，WANG Guanjun，LI Jianmin.Study on dynam⁃ic performance of reactive power compensation in wind power grid connected[J].Power Capacitor and Reactive Power Compensation，2012，33（3）：16-22.

[11]HALILCEVIC S S，GUBINA F，GUBINA A F.The uni⁃form fuzzy index of power system security[J].European Transactions on Electrical Power，2009（9）：360-366.

[16]WANG Shouxiang，ZHANG Jianjun.Fuzzy contingency fil⁃tering and ranking of power system transient stability based on statistical learning[J].Transactions of China Elec⁃tro Technical Society，2016，21（3）：112-117.

[17]HAZRA J，SINHA A K.Prognosis of catastrophic failures in electric power systems[C].Mumbai，India：IEEE Interna⁃tional Conference on Industrial Technology，2016.

[18]BILLINTON R.A reliability test system for educational purpose-basic data[J].IEEE Transactions on Power Sys⁃tem，2009，4（3）：1238-1244.