大规模风电经柔直并网时的系统稳态控制策略

沈同，王通通，宋汉梁

（1.国网陕西省电力公司，陕西西安 710048；2.江苏省配电网智能技术与装备协同创新中心（南京工程学院），江苏南京 211167）

光伏、风电等新能源的规模化开发利用是实现能源可持续发展的主要途径[1-3]，特别是风电的开发利用得到了世界各国政府的高度重视。目前在运行的风电场大多是变速的风电机组，机组使用了结构简单的双馈感应式发电机（doubly-fed induction generator，DFIG）。与定速的感应发电机相比，DFIG的转子转速可以运行在更大的范围内，以捕获尽可能多的风能。DFIG机组输出的功率可以通过转子侧的整流器（rotor side converter，RSC）进行独立控制。与采用全功率换流器的直驱风电机组相比，DFIG机组的换流器容量仅约为机组容量的1/3[1]，换流器的成本显著降低。

随着电网中风电渗透率的不断提升，风电固有的间歇性将对电力系统动态特性以及稳定性产生十分明显的影响，必须加强对风电系统及其接入电网的数学模型进行研究[9]，对系统级的动静态控制策略开展研发，有效提高风电系统的鲁棒性。文献[4]研究了基于矢量控制策略的DFIG数学模型。考虑到矢量控制通常由鲁棒性较好的PI控制器实现，文献[5]通过模糊控制来在线修改PI控制器的参数，实现了动态性能的最优控制。文献[6]则提出利用先进的非线性控制方法来设计DFIG的控制器。从换流器控制策略设计的角度来看，上述控制方法均有效考虑了整个DFIG系统的电磁时间尺度的动态特性。然而对于电力系统机电暂态过程分析而言，电磁时间尺度的动态特性并不是特别重要[7]，因此文献[8]忽略了定子暂态电流以及直流侧电容对系统动态过程的影响，并据此提出了用于电力系统机电时间尺度动态过程分析的简化模型。此外，除了电气动态过程及其控制，机械动态模型对电力系统动态特性也有明显的影响，其通常是暂态响应过程中的低频振荡分量的主要来源。为此，文献[9-10]研究了DFIG风电机组的双质量块轴系模型及其对电网低频振荡特性的影响规律。由于DFIG内部存在低频的轴系振荡模型，因此当外界受扰时，系统会自动激发出与此相关的低频振荡模式，影响电力系统的稳定性。

考虑到风电固有的间歇性，因此通过有效的输电技术将大规模风电安全稳定地送出也是需要深入研究的[7]。从技术特点和工程实际的角度分析，通过将风场的风电就地进行汇集，利用基于电压源型换流器（voltage sourced converter，VSC）的柔性直流输电系统（VSC based DC transmission，VSC-DC）集中送出是解决间歇式风电大规模送出的有效手段[11-12]。但围绕VSC-DC风电送出系统的研究目前还很匮乏，现有的研究工作主要集中于VSC-DC系统对馈入电网的动态支撑技术研究[9]，以提高系统的惯量水平，而系统自身安全稳定运行所需要的稳态控制策略研究较少。

基于此，本文重点研究了大规模风电通过VSC-DC系统并网时的系统级稳态控制策略。提出了用于大规模风电经VSC-DC系统并网时的系统级稳态控制策略，主要包括风电场的站内DFIG机组的 RSC、网侧逆变器（grid-side converter，GSC）稳态控制策略，以及VSC-DC系统的GSVSC、WFVSC稳态控制策略。仿真结果证明了本文提出的系统级稳态控制策略的有效性，可以实现安全稳定地送出风电场的风能。

1 大规模风电经VSC-DC系统接入时的系统结构

含2个VSC的点对点VSC-DC系统的拓扑结构如图1所示。电网侧的VSC经变压器，连接电抗接入交流主网，用于传输风电场发出的有功功率，主要控制与主电网之间交换的无功功率及直流母线电压；风场侧的VSC同样利用变压器接入风场，实现对风电场交流电源电压、频率的有效控制。本文根据图1所示的系统结构，来研究大规模风电经由VSC-DC系统送出时的系统级稳态控制策略。

图1 风电场通过柔直并网时的系统拓扑图Fig.1 The system topology of the wind farm connected to the grid with the flexible DC transmission system

2 风场内DFIG系统的稳态控制策略

风场内DFIG系统的背靠背变流器的控制策略由转子侧整流器RSC和网侧逆变器GSC构成。以下分别给出风场内DFIG系统的稳态控制策略，即RSC控制、GSC控制，如图2所示。

RSC控制部分如图3所示，包含：

1）PQ测量模块：测量图2中M点处的有功、无功功率

2）坐标变换模块：用于实现三相静止坐标系与两相旋转坐标系之间的变换，是矢量控制系统中不可或缺的部分。

3）RSC矢量控制：由较慢的功率控制外环（直流电压控制时间尺度）和较快的电流控制内环（电磁时间尺度）的2个PI控制环级联构成，如图3所示。功率环实现发电机输出的有功、无功功率的控制，电流控制环实现了电机转子电流的控制，使输出电流稳定地达到功率环产生的电流指令，同时通过阈值设置来限制电流过载。

GSC控制部分如图4所示，主要包括：

1）电气测量模块。主要用于测量靠近网侧逆变器处的直流母线电容电压，以及交流侧的并网电流。

2）锁相环（phase locked loop，PLL）测量模块。主要用于测量公共连接点处电网电压的实时相位[13-14]，以完成坐标变换，实现矢量控制。

3）GSC控制模块。主要包含有直流母线电压控制以及网侧无功功率控制，同样由慢速的直流母线电压控制外环（直流电压控制时间尺度）和快速的电流控制内环（电磁时间尺度）级联而成。电容电压控制环主要控制直流母线电容电压达到直流电压指令值Udcref，电流内环控制则可使输出的电流快速地跟踪到直流电容电压控制器给定的电流指令。

图2 DFIG系统层的控制框图Fig.2 DFIG layer control diagram

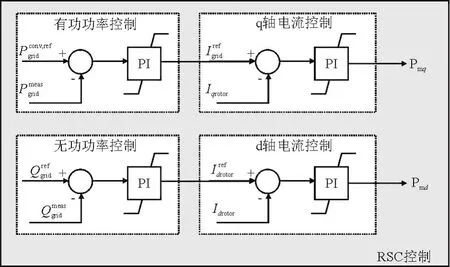
图3 DFIG层的转子侧RSC控制模块Fig.3 DFIG layer rotor side control module

图4 DFIG层的网侧控制模块Fig.4 DFIG layer network side control module

3 风场外VSC-DC系统稳态控制策略

3.1 系统结构模型

图1给出了风电场经由VSC-DC系统送出时的拓扑结构，其中300 MW的大规模风场由150台容量均为2 MW的DFIG构成，直流输电电缆由简化的RL电路来等效模拟。风场侧整流器（wind farm VSC，WFVSC）的主要功能是收集大规模风场发出的电能。WFVSC的作用是实现风场电网的恒压恒频，而网侧的逆变器（grid side VSC，GSVSC）主要实现直流母线电容电压的稳定，同时控制其与接入电网之间交换的无功功率。

3.2 GSVSC控制策略

网侧逆变器GSVSC的控制策略如图5所示，依然采用典型的电网电压定向的坐标系，即d轴定位于电网电压矢量。PLL用于测量网侧电压的实时相位θPLL。显然，直流母线电容电压与id有关；无功功率与iq有关[9]，据此可设计GSVSC的控制策略。控制器由2个级联的控制环路构成，其中外环控制器用于控制直流母线电容电压，同时控制其与接入电网之间的无功功率。直流母线电容电压的指令值为恒定值，即VSC-DC系统设计的额定电压。此外，为了抑制换流器发生过流故障，还需要根据变流器的过载量设置id、iq的阈值。

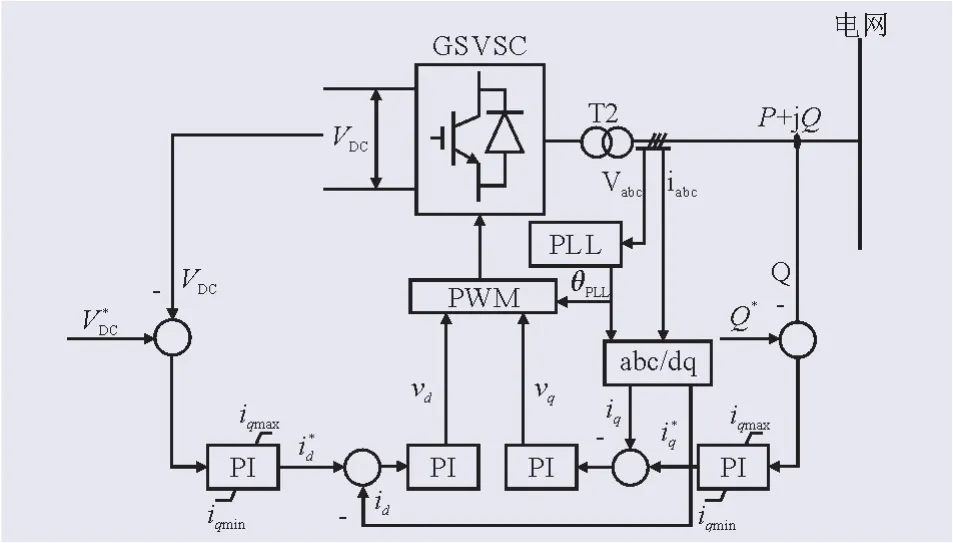
图5 网侧逆变器控制策略Fig.5 GSVSC control strategy diagram

3.3 WFVSC控制策略

由于大规模风电场区域内基本没有负荷，因此可让大规模风电场交流电网在给定频率下运行。此外，由于DFIG机组背靠背变频器的响应时间一般小于5 ms，因此风电场的电网频率几乎不影响其有功功率，风场内的整流器可在给定的电网电压（给定的幅值和频率）下稳定运行，其控制策略如图6所示。风电场侧整流器的频率指令值保持恒定[12]。风电场电网电压的幅值通过电压外环控制和电流内环控制实现。此外，该控制模式还能在风场内发生故障时有效地限制故障电流，确保系统安全稳定。

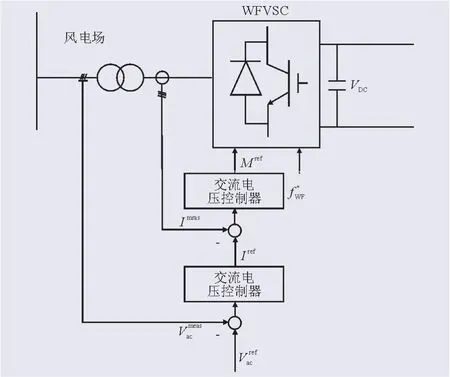
图6 风场侧整流器控制策略Fig.6 Diagram of the WFVSC control strategy

4 仿真验证

为了验证本文提出的稳态控制策略的有效性与先进性，在仿真软件DIgSILENT中搭建了图1所示的两端测试系统，并在风速阶跃工况、随机风速工况下进行了仿真分析，系统的主要参数如表1所示。

表1 仿真系统的主要参数Tab.1 Example system main parameters

4.1 风速阶跃工况

图7为风电系统在风速阶跃工况下的仿真结果。在该工况下，初始风速为8 m/s，然后以2 m/s的速度，每隔45 s变化一次。仿真结果表明：由于VSC-DC系统使送端电场和受端电网之间实现了功率解耦，因此风电场的特性与DFIG机组的输出特性相近。图7(b)至图7(d)的仿真结果表明，随着风速的不断阶跃增大，风电场的出力也不断地增大；与此同时，为了实现最大的风功率吸收，DFIG的转子转速也相应地不断地变化；风速过高时，风电场将会启动桨距角控制策略来限制发电机转子转速。图7(e)至图7(f)的仿真结果表明，直流母线电压在风速阶跃工况下有小范围的波动（小于1%）；风电场的电网电压以及场内电网频率的波动幅度也都在合理范围之内。与此同时，接入网侧的逆变器的功率特性与风场内换流器的功率特性相近。此外，系统的有功功率小于1 pu，该误差是因为VSC-DC系统本身的运行也存在着功率损耗所致。

4.2 随机风速工况

图8、图9均为随机风速工况下系统的仿真结果。图8中的平均风速为9 m/s，方差为2 m/s；图9中的平均风速为14 m/s，方差为1 m/s。对比2种工况下的仿真结果可知，本文提出的稳态控制策略很好地实现了大规模风电通过柔性直流输电系统并网。场内整流器侧交流电网的频率和电压均运行在合理的范围之内。直流母线电压的波动范围也在2%以下。如果没有本文所述的控制策略投入运行，那么受端电网吸收的有功功率将随着风场的功率波动而不断波动，致使受端电网的电能质量恶化，甚至危及受端电网的安全稳定性。

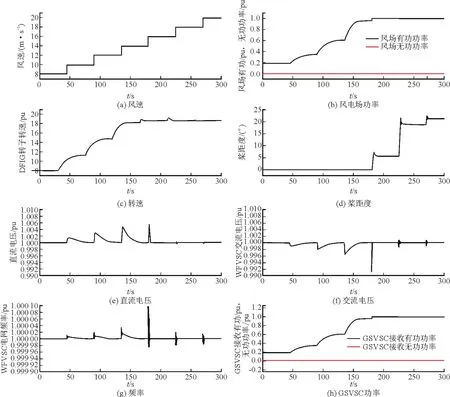
图7 风速阶跃工况Fig.7 Response of the system under wind speed step

图8 随机风速工况（平均风速为9 m/s，方差为2 m/s）Fig.8 The response under random wind speed（average wind speed is 9 m/s,variance is 2 m/s）

图9 随机风速工况（平均风速为14 m/s，方差为1 m/s）Fig.9 The response under random wind speed（average speed is 14 m/s and variance is 1 m/s）

5 结论

本文提出了大规模风电场由柔直输电系统送出风电时的系统级稳态控制策略，包括场站内DFIG的转子侧整流器、网侧的逆变器稳态控制策略，以及风场外VSC-DC系统的网侧逆变器、风场侧整流器的稳态控制策略；网侧逆变器控制直流母线电容电压，以及与接入电网之间的无功功率；风电场侧整流器控制场内电网电压的幅值和频率，以稳定风电场内的电网电压。DFIG机组在额定风速工况下可实现最大功率跟踪；超出额定风速范围时，系统可通过桨距角控制来限制发电机转速。典型风速工况下的仿真结果表明了本文提出的稳态控制策略能确保系统稳定地送出风电场的风能。

参考文献

[1]吴俊宏，艾芊.多端柔性直流输电系统在风电场中的应用[J].电网技术，2009，33（4）：22-27.WU Junhong，AI Qian.Research on multiterminal VSCHVDC system for wind-farms[J].Power System Technolo⁃gy，2009，33（4）：22-27（in Chinese）.

[2]PEAN R，CLARE J C，ASHER A G M.Doubly fed induc⁃tion generator using back to back PWM converters and its application to variable speed wind energy generation[J].Proceedings of the Electric Power Applications，1996，143（3）：56-73.

[3]熊连松，刘小康，卓放，等.光伏发电系统的小信号建模及其控制器参数的全局优化设计方法[J].电网技术，2014，38（5）：1234-1241.XIONG Liansong，LIU Xiaokang，ZHUO Fang，et al.Small signal modeling of photovoltaic power generation sys⁃tem and global optimal design for its controller parame⁃ters[J].Power System Technology，2014，38（5）：1234-1241（in Chinese）.

[4]EKANAYAKE J B.Dynamic modeling of doubly fed induc⁃tiongeneratorwindturbines[J].IEEETransactionsonPower Systems，2003.18（2）：803-809.

[5]ALMEIDA R G，LOPES J A P，BARREIROS J A L.Improving power system dynamic behavior through doubly fed induction machines controlled by static converter using fuzzy control[J].IEEE Transactions on Power Systems，2004，19（4）：1942-50.

[6]FENG Wu，ZHANG X P，PING J，et al.Decentralized nonlinear control of wind turbine with doubly fed induction generator[J].IEEE Transactions on Power Systems，2008，23（2）：613-621.

[7]XIONG L，ZHUO F，WANG F，et al.Static synchronous generator model：a new perspective to investigate dynamic characteristics and stability issues of grid-tied pwm inverter[J].IEEE Transactions on Power Electronics，2016，31（9）：6264-6280.

[8]FEIJOO A E A.A third order model for the doubly-fed in⁃duction machine[J].Electric Power Systems Research，2000，56：121-127.

[9]WEI Qiao.Dynamic modeling and control of doubly fed in⁃duction generators driven by wind turbines[C]//Power Sys⁃tems Conference and Exposition，2009：1-8.

[10]ENGELHARDT S，ERLICH I，FELTES C，et al.Reac⁃tive power capability of wind turbines based on doubly fed induction generators[J].IEEE Transactions on Energy Con⁃version，2011，26（1）：364-72.

[11]徐政，陈海荣.电压源换流器型直流输电综述[J].高电压技术，2007，33（1）：1-10.XU Zheng，CHEN Hairong.Review and applications of VSC HVDC[J].High Voltage Engineering，2007，33（1）：1-10（in Chinese）.

[12]陈海荣，徐政.向无源网络供电的VSC-HVDC系统的控制器设计[J].中国电机工程学报，2006，26（23）：42-47.CHEN Hairong，XU Zheng.Control design for VSCHVDC supplying passive network[J].Proceedings of the CSEE，2006，26（23）：42-48（in Chinese）.

[13]XIONG L，ZHUO F，WANG F，et al.A novel fast openloop phase locking scheme based on synchronous reference frame for three-phase non-ideal power grids[J].Journal of Power Electronics，2016，16（4）：1513-1525.

[14]龚锦霞，解大，张延迟.三相数字锁相环的原理及性能[J].电工技术学报，2009，24（10）：94-99.GONG Jinxia，XIE Da，ZHANG Yanchi.Principle and performanceofthethree-phasedigitalphase-lockedloop[J].Transactions of China Electrotechnical Society，2009，24（10）：94-99（in Chinese）.