基于高斯混合模型和交叉熵的电网可靠性评估算法

罗建勇，赵客壮

（1.国网铜川供电公司，陕西铜川 727031；2.国网宝鸡供电公司，陕西宝鸡 721004）

电网可靠性评估即量化评估电网当前或未来的可靠性水平，其不仅能提供客观的量化指标，还能预测系统失效的方式及后果的严重性[1]。电网可靠性评估主要包括发电系统、配电系统和发输电组合系统3个层面[3-4]的可靠性。

电网的可靠性是指电网按照用户的需求和一定质量标准提供电能能力的度量，包括安全性与充裕度2个方面[5-6]。其中，安全性是指电网运行时抵抗局部或大范围扰动的能力；充裕度是指电网在母线电压和系统频域约束下，向用户提供所需电能的能力[7-8]。

目前，电网可靠性评估方法主要分为状态解析法[9]、蒙特卡罗模拟法[10]和混合法[11]。状态解析法通过解析计算和故障枚举获得电网可靠性指标，但其较难获得持续时间和频率指标；蒙特卡罗模拟法以概率统计理论为基础，不依赖系统的复杂程度和规模，更适合风电和光伏发电等新型电力系统，但其需要较大的计算量且收敛速度慢[12-13]；混合法则通过结合模拟法和解析法来加快模拟法的收敛速度。

为了同时满足模拟法的精度和速度需求，本文结合高斯混合模型与交叉熵原理[14-15]，提出了基于混合高斯建模和交叉熵重要性抽样的电网可靠性评估方法。该方法首先对电网节点负荷、光伏发电站光照强度或风电场风速等变量建立混合高斯模型；然后使用该模型进行重要性抽样，得到负荷样本；最后将负荷样本分摊到各电网节点上，并计算系统的负荷削减概率及期望缺供电量来评估电网的可靠性。

1 基于高斯混合模型和交叉熵的可靠性评估方法

高斯混合模型被广泛应用于混沌系统控制、图像识别和语音识别等领域，其是一种融合了参数模型与非参数模型的概率密度估计方法，具有准确描述任意连续型随机变量的联合概率密度分布的优点[13]。本文使用高斯混合模型对电网节点负荷、光伏发电站光照强度或风电场风速等变量进行建模，高斯混合模型可以用式（1）表示

式中：使用估计数据的总体分布，高斯分量的个数为K。第k个高斯分量由其权值w、方差和均值μk表示为：

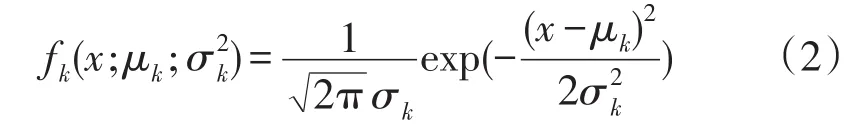
本文用向量v表示高斯混合模型的所有参数，并使用最小交叉熵原理估计参数数值。传统的基于单一概率密度函数的交叉熵重采样方法只能更新参数向量v，而无法更新权值向量。因此，本文提出了一种基于混合高斯模型的重采样方法，用于同时更新模型的参数和权值。模型参数更新过程可转化为求解式（3）所示的最小值问题。

式中：Xi(i=1,2,…,N)是某一轮更新中的概率密度函数抽样得到的样本。其中，gmin(X)通过更新权重参数v1,v2,…,vk得到。第j个高斯模型的参数vj的更新过程如下。

1）将式（3）对vj求导可得：

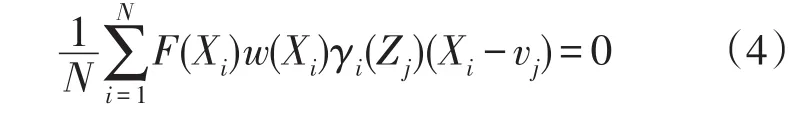
其中γi(Zj)如下：

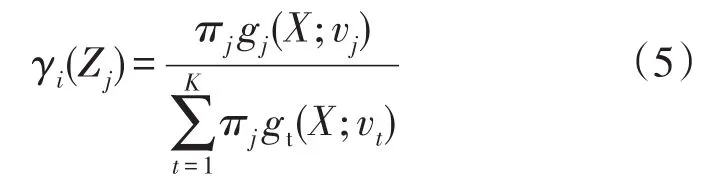
2）将式（5）带入式（4）可得vj的更新表达式为：

权重更新过程可由式（3）对w求导得到，如式（7）所示：

根据式（6）和式（7）迭代更新vj和wj，直至其满足迭代终止条件，计算得到最优参数vopt-1,vopt-2，…,vopt-k和最优权重πopt-1,πopt-2,…,πopt-k，进而可求得高斯混合模型为：

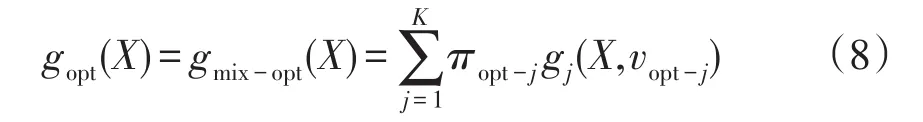
将本文求得的高斯混合模型用于电网可靠性评估具体流程，如图2所示。首先读取电网的拓扑结构和各元件信息，初始化模型参数；然后进行第一阶段采样并计算，得到最优模型参数；再根据求得的模型估计系统的状态，更新可靠性指标值；最后，当迭代过程满足终止条件时，停止更新并输出电网各可靠性指标。

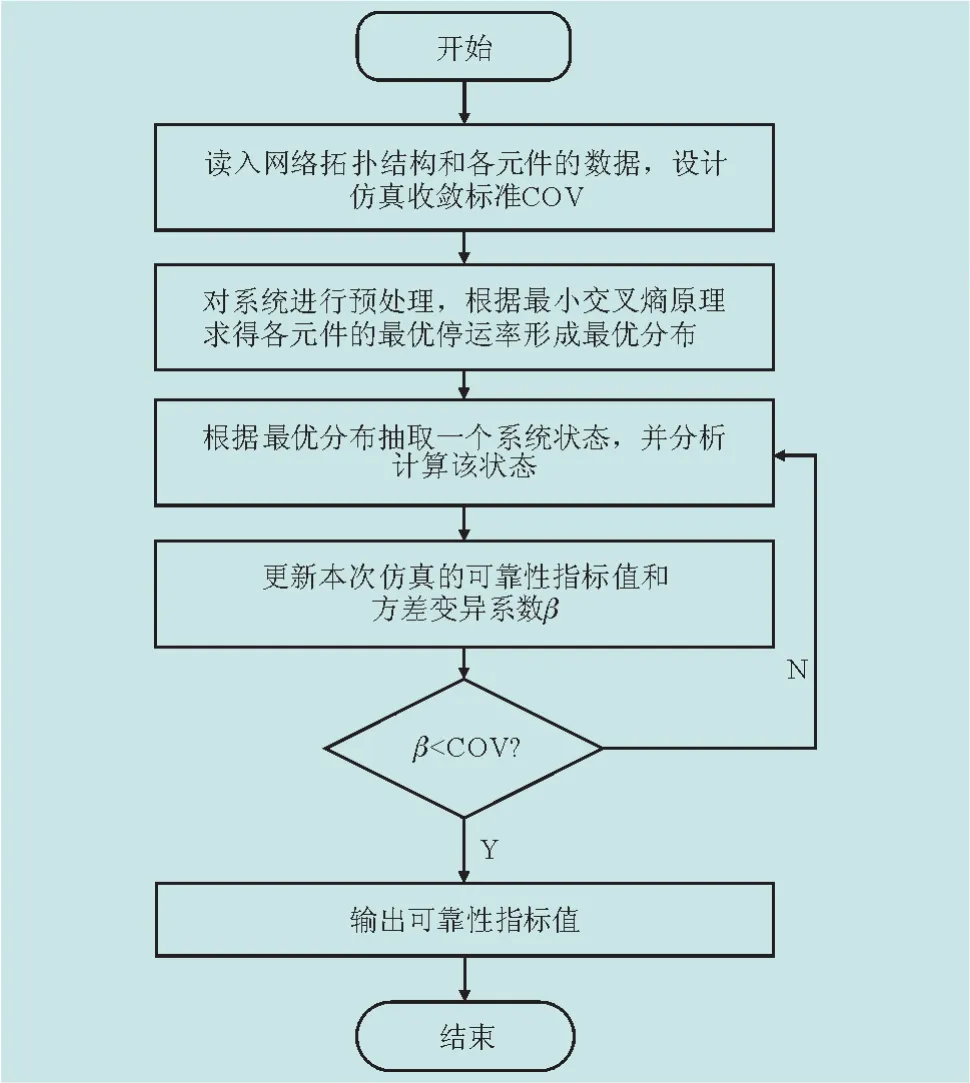
图1 可靠性评估流程Fig.1 Process of the reliability evaluation

2 算例分析

本部分首先建立负荷随机波动的概率模型，然后评估IEEE-RTS79[13]系统的可靠性，并从评估的有效性和计算速度2个方面验证本文所提出的方法。

文献[13]给出了IEEE-RTS79系统的年时序负荷曲线。本文对该组数据建立高斯混合模型，并确定高斯模型的个数为4，计算得到各模型的参数如表1所示。

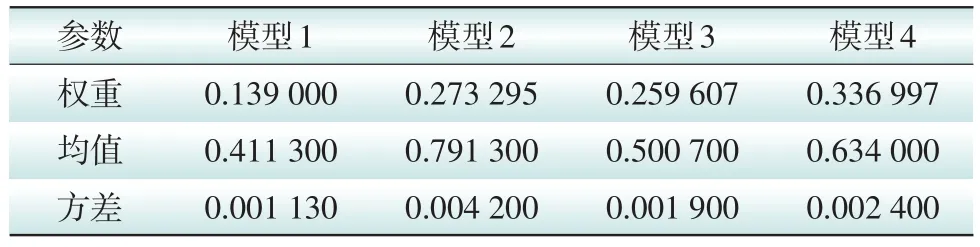
表1 高斯混合模型参数Tab.1 Parameters of the Gaussian Mixture Model

使用本文算法和文献[12]提出的基于蒙特卡洛采样的方法分别对IEEE-RTS79系统进行可靠性评估，并计算系统的负荷削减概率（PLC）和期望缺供电量（EENS），实验结果如表2和表3所示。从表中可以看出，2种算法在采样阶段I后均能有效地计算高斯混合模型的参数。这2种算法的主要区别是阶段I所采样的样本数，本文算法只需采样14 000以上的样本，而文献[12]至少需要50 000个样本才能进行有效地评估。同时从表中还可以看出，提高阶段I的采样数可提升阶段II的处理效率。比较2种算法的可靠性评估指标PLC和EENS可知，2种算法的可靠性指标均能满足准确性要求。

可以看出，本文算法比文献[12]的算法需要的采样数更少，计算效率更高，且能确保电网可靠性指标的准确性。

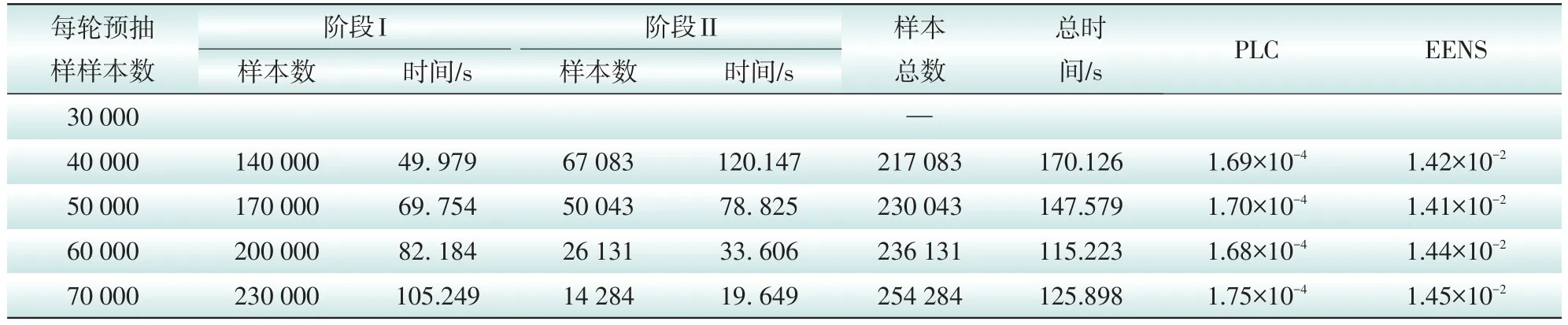
表2 本文算法评估结果Tab.2 The evaluation results of the algorithm proposed in this paper

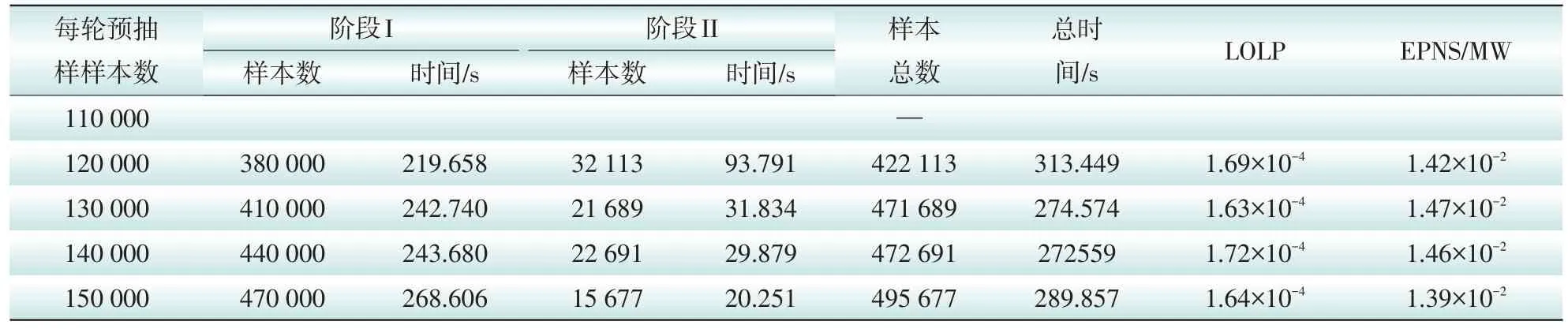
表3 文献[12]评估结果Tab.3 Evaluation results of Literature[12]

3 结语

本文结合高斯混合模型和交叉熵原理，提出了基于混合高斯建模与交叉熵重要性抽样的电网可靠性评估方法。该方法首先对电网节点负荷、光伏发电站光照强度或风电场风速等变量建立混合高斯模型，得到负荷样本，从而能有效实现计算效率和精度的综合兼顾；然后使用该模型进行重要性抽样，可以较快速地生成多维变量的随机样本；最后将负荷样本分摊到各电网节点上，并计算系统的负荷削减概率和期望缺供电量来评估电网的可靠性。在IEEE-RTS79系统上的仿真测试结果表明，该方法能精确高效地评估电网的可靠性。

参考文献

[1]BILLINTON R，LI WENYUAN.Reliability assessment of electric power system using Monte Carlo method[M].Lon⁃don：Plenum Press，1994.

[2]李生虎，于丽萍，董王朝.含TCSC电力系统可靠性非同调分析[J].电力系统保护与控制，2016，44（14）：1-7.LI Shenghu，YU Liping，DONG Wangchao.Analysis of reliability non-coherence of power systems with TCSC[J].Power System Protection and Control，2016，44（14）：1-7.

[3]邓奥攀，胡志坚，胡美玉，等.同时计及设备老化与不完全维修的电力系统可靠性评估[J].电力系统保护与控制，2017，45（3）：69-74.DENG Aopan，HU Zhijian，HU Meiyu，et al.Power sys⁃tem reliability evaluation considering deterioration and im⁃perfect maintenance of equipment[J].Power System Protec⁃tion and Control，2017，45（3）：69-74.

[4]李铭钧，王承民，欧郁强，等.全网供电可靠性指标合成研究[J].电网与清洁能源，2014，30（2）：28-32.LI Mingjun，WANG Chengmin，OU Yuqiang，et al.Syn⁃thesis method for the reliability indicators of the distribu⁃tion network[J].Power System and Clean Energy，2014，30（2）：28-32.

[5]SIGuangye，CORDIER J，KENNELR M.Extending the power capability with dynamic performance of a powerhardware-in-the-loop application-power grid emulator us⁃ing“inverter cumulation”[J].IEEE Transactions on Industry Applications，2016，52（4）：3193-3202.

[6]GONGM，ZHOUL，ZHANGC，etal.Researchofreliability evaluation method of distributed generation supply power forcoalmine[J].Industry&MineAutomation，2016，42（1）：23-27.

[7]高小童，秦志龙.基于混合Copula函数的含风电场电力系统可靠性评估[J].山东电力技术，2016，43（8）：25-28.GAO Xiaotong，QIN Zhilong.Reliability evaluation of power system with wind farms based on mix-Copula func⁃tion[J].Shandong Electric Power，2016，43（8）：25-28.

[9]李莉，高丽媛，赵旷怡.基于PMC模型的电力光纤传输网可靠性诊断方法[J].电子设计工程，2016，24（14）：94-96.LI Li，GAO Liyuan，ZHAO Kuangyi.A reliability diagno⁃sis method for electric power optical fiber transmission net⁃workbasedonPMCmodel[J].ElectronicDesignEngineering，2016，24（14）：94-96.

[10]吴英帅.基于继电保护隐性故障的电力系统可靠性分析[J].通讯世界，2016（23）：226-227.WU Yingshuai.Reliability analysis of power system based on relay protection recessive fault[J].Telecom World，2016（23）：226-227.

[11]陈明帆，石佳，宁光涛，等.基于数据库的电力系统规划与可靠性评估数据平台开发[J].电网与清洁能源，2014，30（5）：1-6.CHEN Mingfan，SHI Jia，NING Guangtao，et al.Develop⁃ment of power system planning and reliability analysis da⁃tabase platform based on database[J].Power System and Clean Energy，2014，30（5）：1-6.

[12]LEITED S A M，FERNANDEZ R A G，SINGH C.Gener⁃ating capacity reliability evaluation based on monte carlo simulation and cross-entropy methods[J].IEEE Transac⁃tions on Power Systems，2010，25（1）：129-137.

[13]Subcommittee P M.IEEE reliability test system[J].IEEE Transactions on Power Apparatus&Systems，1979，PAS-98（6）：2047-2054.

[14]王思思，任世卿.一种改进的基于混合高斯模型的运动目标检测算法[J].计算机科学，2015，42（S2）：173-174.WANG Sisi，REN Shiqing.Improved moving target detec⁃tion algorithm based on gaussian mixture model[J].Com⁃puter Science，2015，42（S2）：173-174.

[15]安曦宁.基于改进混合高斯模型的人群密度估计研究[J].电子科技，2017，30（5）：180-183.AN Xining.Improved hybrid model of crowd density esti⁃mationbasedonGauss[J].ElectronicScienceandTechnology，2017，30（5）：180-183.