剖析个案，感悟类比思维之魅力

易大中+宋红霞

学生个案

“老师，我通过了二中创新班的考试！”QQ上出现了一条报喜的信息，也就意味着一场面对市初三学生进行的50名精英选拔考试，学生陈通过了！学生陈在我五年的数学教学中，是一个总能给我的课堂带来精彩的学生。停下手中的活，师生之间开始了一番对话。

【对话摘要】2016年6月，学生陈临近初中毕业。

生：老师，我通过了二中创新班的考试！数学好难，但是考得不错！

师：哇，你好棒！恭喜你！

生：您还记得吗？曾经我提出一猜想：扇形面积就是弧长乘半径除以2！其实那个圆环面积也可以是（内圆周长+外圆周长）×（外圆半径-内圆半径）÷2。说扇形可以理解为曲边三角形，圆环就可以理解为曲边梯形。这些都是一条藤上的。（传过来两张图，如图所示）式子展开后与标准算式一致。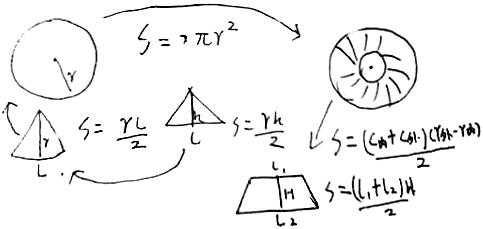

……

看着他传过来的两张图和两句话“这些都是一条藤上的”“式子展开后与标准算式一致”，震撼之余，作为教师的我也陷入了沉思，三年前精彩的一幕又再现眼前。

【精彩回放】2013年6月，学生陈临近小学毕业。

正在进行平面图形面积整理与复习教学，学生陈一脸疑惑地举着手。往往此时，我都会给他机会，因为作为一个爱提问题的孩子，他的问题总能带给我们一次精彩的辩论或有意义的探究活动。果不其然———

生：我猜想扇形面积就是弧长乘半径除以2，对不？

师：说说你猜想的理由。

生：在圆面积公式推导过程中，我们可以设想将圆剪成很多个等分的三角形再拼成一个长方形，两个一样的扇形同样可以拼成长方形，面积不就是弧长乘半径除以2？

正当我想回应时，他接着说：“如果是对的，那么圆的面积也可以是圆周长乘半径除以2！”……从猜想的理由，到“如果……那么……”的推理，很明显，他是对的。

至于对话中提过“圆环面积就是内外两个圆的周长乘半径差除以2”一事，的确问过，只记得当时有个学生说“这也太复杂了吧！”而我可能因为从没去想过，或是认同了后者说的复杂，“敷衍了他”。现在想想实觉惭愧！

剖析与思考

再思考与学生陈的对话和片段回想时，一个关于数学思维能力的核心词“类比思维”突显在脑中，再加以剖析，对于类比思维的认识也随之越来越明晰。

学生陈根据类比，认为扇形与圆形都可以等分成若干个小三角形再拼成一个长方形，将圆面积公式推导方法迁移到扇形面积公式推导上，这就是合情推理中的类比推理。类比推理就是依据两个对象之间有着某些相同或相似的属性，推出它们存在其他相同或相似属性的思维方法。根据学生陈的思维呈现，类比推理可以表示如下：

这样看来，一个类比原型应该包括新问题和原问题两个部分。原问题与新问题之间是平行的，在解决新问题之时联想到与之相似的原问题，通过已经掌握的、非常熟悉的原问题，类比解决新问题。

波利亚曾形象地说：“类比是一个伟大的领路人。”通过学生陈，我才真正明白这句话的意义所在：一是类比能促进学生自主学习与创新意识的培养；二是像学生陈将所有平面图形想象成一个梯形，根据这些平面图形的相似性，类比推理得出最基本的面积公式“（上底+下底）×高÷2”的行为，能建构完整的数学知识结构，形成知识网络。这应该就是类比的魅力所在，这魅力也让我对类比思维的渗透与引导有了一些思考。

1.引导学生运用类比思维之时，注重作类方法整理。

数学课程的各个领域都提供了丰富的让学生生成类比思维的素材。教学中，我们应该充分调动学生的已有经验，引导学生运用自己认为与当前学习内容相似的、已学会的知识与方法进行学习。如，小数、分数的运算定律的学习，可以引导学生回忆整数运算定律的建构过程再进行自主探究，最后通过回顾与整理，有意识地让学生形成“辨别—分化—类化—抽象—检验—概括—符号化”的概念学习类方法。这种类方法才是剔除知识之外，最有价值的科学研究元素。

2.学生自主建构类比之时，注意给予时空验证。

3.运用类比思维建构的知识网络，作横纵引导。

当知识构建成网络，知道知识之間的内在联系时，学生就能从更高的角度整体把握知识，使知识得到横向拓宽或纵向递进的深化。比如，学生陈运用类比思维对平面图形面积的整理与建构，我们可以思考立体图形体积的整理与建构，其中就圆柱体积的探究，运用类比，可以充分调动学生回顾原问题长方体、正方体体积公式探究过程，产生对新问题圆柱体积公式的猜想：圆柱体积也是底面积乘高。在给予充足的时空验证时，又可以以此为新问题，让学生联想相似的原问题———圆面积公式的推导，通过剪拼将圆柱体转换成长方体，找寻联系，得出结论。在作整体建构时，让学生思考为什么都可以是“立体图形的体积等于底面积乘以高”？如果是这样，那么圆锥的体积还能是底面积乘高吗？……这样的探究过程，学生不仅学会，更指向学生会学。

这样看来，在数学教学中运用类比，可以让数学学习更容易、更生动有趣。同时，长期的引导与渗透，不仅有利于学生数学知识的网络建构，更有利于学生自主探索与创新思维的培养，不愧是“数学学习伟大的引路人”！

【本文是湖南省教育科学“十二五”规划课题“区域推进义务教育阶段数学教与学衔接的实践研究”（课题批准号：XJK013CZXX065）研究成果】

（作者单位：株洲市荷塘区星光小学）