求解非线性方程组的新的信赖域方法①

唐江花

(安徽新华学院通识教育部，安徽合肥230088)

求解非线性方程组的新的信赖域方法①

唐江花

(安徽新华学院通识教育部，安徽合肥230088)

通过将信赖域技巧与Levenberg-Marquardt算法有效结合到一起，进而提出新的信赖域方法，进而证明了新方法的全局收敛性，并且在局部误差界等条件下得到该算法的收敛阶为2δ2+δ,其中δ∈(1/2,1)并且给出了数值结果，在证明新方法的相关收敛性结果时，同时进行了数值实验，并验证了新的信赖域方法的可行性.

非线性方程，全局收敛性，新的依赖域方法

0 前言

考虑非线性方程组

F(x)=0，

(1)

其中F(x):Rn→Rm是连续可微的函数.文中定义X*作为F(x)的非空解集，‖·‖代表2-范数，F(x)具有非线性特点.

Levenberg-Marquardt(LM)方法[1-5]在求解非线性方程组的方法中是比较经典的一种方法，其迭代步为

(2)

将它当作是Guass-Newton方法的一种修正，将参数λk进行引入，进而克服Guass-Newton法中矩阵J(x*)必须满秩的要求.

Fang[6-8]两步牛顿法的启示下，同时为了节约雅克比矩阵的计算，提出了一种改进的LM算法(MLM)，该算法的提出，不仅可以对经典的LM步进行计算，还可以对近似LM步进行计算.

(3)

此种算法由于局部误差阶条件的原因拥有3阶收敛性.

与此同时，Yang[7]在文献[6]的基础之上，为了使雅克比矩阵的计算更加节约以及拥有更快的收敛速度，提出了一种高阶的LM算法(HMLM)，又添加了一步接近于LM步.

(4)

此种算法受到局部误差阶条件，拥有4阶收敛性.

Chen[9]为了可以有效地掌控步长，对Fan和Yank的研究思想进行整合后提出了一种高阶的修正LM算法.

(5)

受此启示，在求解非线性方程组时为了减少更多的Jacobi矩阵计算，本文将在文献[9]研究思想之上再增添一步近似LM步，

(6)

进而得出一种新的Levenberg-Marquardt算法.

1 非线性方程组的改进信赖域算法的提出

式(1)的目标函数为

Φ(x)=‖F(x)‖2.

(7)

提出了一个信赖域半径趋于0的信赖域算法.对于下面的子问题通过迭代进行求解.

(8)

得出试探步.

下文为文献[10]中的信赖域算法.

算法1 (1)设x1∈Rn,00，M》C4μ1,Δ1=‖F1‖δ,k:=1.

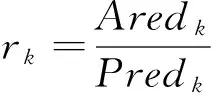
计算Δk+1=μk+1‖Fk+1‖δ.

(4)令k=k+1由此转到第二步.

此种算法是全局收敛的，它的收敛速度在局部误差有界的条件下为2δ.

本文提出的新的信赖域算法是在Levenberg-Marquardt方法的启示上所提出来的，新的信赖域算法在每次迭代中首先对下面的子问题进行求解

(9)

得到dk，令yk=xk+dk,进行求解

(10)

(11)

Predk=‖Fk‖2-‖Fk+Jkdk‖2+‖F(yk)‖2-‖F(yk)+Jkdk‖2，

(12)

而将实际下降量和预估下降量之间的比值rk定义为

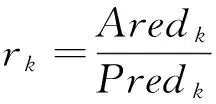
(13)

新的信赖域的算法如下所示.

算法2 (1)设x1∈Rn,00，M》C4μ1,Δ1=μ1‖F1‖δ,k:=1.

(14)

(3)取

(15)

计算

Δk+1=μk+1‖Fk+1‖δ.

(16)

(4)令k:=k+1并且转到第(2)步.

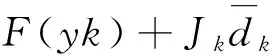
(17)

通过上面计算的结果得出下面的引理.设dk为式(9)的解，则预估下降量有如下估计

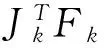
(18)

2 新Levenberg-Marquardt算法的全局收敛性的验证

接下来对新算法的全局收敛性进行讨论，为了得到全局收敛性结果，做出如下情形假设:

情形1F(x)是连续可微的，且F(x)和Jacobian矩阵J(x)是Lipschitz连续的，也就是说，存在正常数L1和L2使得

‖J(y)-J(x)‖≤L1‖y-x‖, ∀x,y∈Rn

(19)

和

‖F(y)-F(x)‖≤L2‖y-x‖, ∀x,y∈Rn.

(20)

定理1在假设情形1的条件下，由算法忍.忍产生的迭代序列满足

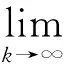
(21)

证明由情形1，我们可以得到

‖F(y)-F(x)-J(x)(y-x)‖≤L1‖y-x‖2, ∀x,y∈Rn.

(22)

我们用反证法证明.假设定理结论不正确，则存在一个正常数∈>0和无穷多个k使得

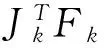
(23)

令I={k|rk≥c1)}.则有

(24)

由(19)和(20)知

(25)

第一种情况，若I有限，由式(17)知，对充分大的k有μk+1=c3μk.由于c3<1，我们得到

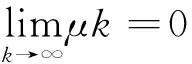
(26)

第二种情况，若r无限，则由(17)知

(27)

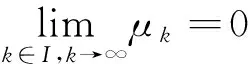
(28)

由于当k∉I时，c3<1且μk+1=c3μk.所以当I是无限时，这时式中式依旧成立.即

(29)

由‖Fk+1‖≤‖Fk‖,‖dk‖≤Δk且Δk=μk‖Fk‖δ,由式(7)和式(29)可以得到

(30)

此外，由式(8)和式(30)可得

(31)

=part1+part2+part3.

(32)

因此，由于part1和part2收敛到.，我们只需证明part3收敛到0.

由于

(33)

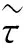
3 数值实验

表1 r(J(x*))=n-1

[1]LevenbergK.Amethodforthesolutionofcertainnon-linearproblemsinleastsquares[J].QuarterlyofAppliedMath-matics，1944,2(1):164-168.

[2]MarquardtDW.Analgorithmforleast-squaresestimationofnonlinearparameters[J].JournaloftheSocietyforIn-dustrialandAppliedMathematics，1963，11:431-441.

[3]MoreJJ.TheLevenherg-Marquardtalgorithm[C].//LectureNotesinMathematics，1977，11(1):101-110.

[4]MoreJJ.Recentdevelopmentsinalgorithmsandsoftwarefortrustregionmethods[M].SpringerBerlin:MathematicalProgrammingtheStateoftheArt, 1982.

[5]ChenLiang.Ahigh-ordermodifiedLevenherg-Marquardtmethodforsystemsofnonlinearequationswithfourth-orderConvergence[J].AppliedMathematicsandComputation,2016,24:78-83.

[6]FanJinyan.ThemodifiedLevenherg-Marquardtmethodfornonlinearequationswithcubicconvergence[J].MathematicsofComputation,2012,81(277):447-466.

[7]YangXiao.Ahigher-orderLevenherg-Marquardtmethodfornonlinearequations[J].AppliedMathematics&Computa-tion, 2013，219(7):10 682-10 694.

[8]FanJinyan.AcceleratingthemodifiedLevenherg-Marquardtmethodfornonlinearequations[J].MathematicsofComputa-tion,2014,83:1 173-1 187.

[9]ChenLiang.AmodifiedLevenherg-Marquardtmethodwithlinesearchfornonlinearequations[J].ComputationalOptimi-zation&Applications,2016,65 (3):1-27.

[10]FanJY.ConvergenceRateofTheTrustRegionMethodforNonlinearEquationsUnderLocalErrorBoundCondition,COAP,2006，34:215-227

[11]FanJY.AmodifiedLevenberg-Marquardtalgorithmforsingularsystemofnonlinearequations[J].JournalofComputationalMathematics, 2003,21:625-636

[12]FanJinyan.AcceleratingthemodifiedLevenherg-Marquardtmethodfornonlinearequations[J].MathematicsofComputa-tion, 2014,83:1 173-1 187.

[13]ChenLiang.AmodifiedLevenherg-Marquardtmethodwithlinesearchfornonlinearequations[J].ComputationalOptimi-zation&Applications,2016,65(3):1-27.

[14]MoreJJ,GarbowBS,HillstromKE.Testingunconstrainedoptimizationsoftware[J].ACMTransactionsonMathematicalSoftware，1981,7(1):17-41

[15]SchnabelRB,FrankPD.Tensormethodsfornonlinearequations[J] .SiamJournalonNumericalAnalysis，1984,21(5):815-843.

[16] 路娜. 非线性方程组的改进信赖域算法[D].上海：上海交通大学,2014.

The New Trust Region Method for Solving the System of Nonlinear Equations

TANG Jiang-hua

(Department of General Education, Anhui Xinhua University, Hefei 230088，China)

Through the combine of the new trust region technique and Levenberg-Marquardt algorithm together, it put forward a new trust region method. It proved that the global convergence of the new method, and under the local error bound condition it obtained the convergence order of the algorithm 2δ2+δ,andδ∈(1/2,1),andthenumericalresultsarepresented.Itnotonlyprovedtherelevantconvergenceresultsofthenewmethod,butalsogavethenumericalexperiments,andverifiedthefeasibilityofthenewtrustregionmethod.

nonlinear equation，global convergence，new domain dependent method

2016-11-06

安徽省高等数学教学团队(2016jxtdx03)；安徽省高等数学名师工作室(2014msgzs168)；安徽新华学院第八批骨干教师培养对象(2015xgg29)；校级科研项目(2016zr003)资助

褚正清，E-mail：798116049@qq.com.

O

A

1672-6634(2017)01-0038-06