渗透数学思想方法的教学策略

顾晓华，江苏省无锡市五爱小学教师，江苏省第十一批特级教师，江苏省第四期“333高层次人才培养工程”培养对象。积极践行“返璞归真教数学”，让小学数学课堂回归教与学的自然状态。领衔两轮原无锡市北塘区“小学数学名师工作室”，主编了北塘区教育局名师工作室丛书《成长的秘密：有你同行》。

[摘 要]让学生掌握数学思想方法是数学教育最核心的任务。在小学数学教学中，要通过化繁为简、重视细节、游戏、故事、数学活动、梳理和反思等策略，使学生获得学习动力，快乐地学习数学，自然而然地掌握数学思想方法。

[关键词]数学思想；渗透；教学策略

画龙点睛的故事中，点睛之后的龙有了灵性，从供人观赏的壁上丹青变成了可以自由腾飞的超级神物。这个故事对数学教学的启发是 ：数学知识、公式、解题模式，都只是雕虫小技，让学生掌握数学思想方法，才是“点睛之笔”。

一、化繁为简，宏观渗透

史宁中教授在《数学思想概论》中提出，数学发展所依赖、所依靠的思想在本质上有三个：抽象、推理、模型，其中抽象是最核心的。通过抽象，在现实生活中得到数学的概念和运算法则，通过推理得到数学的发展，然后通过模型建立数学与外部世界的联系[1]。对于这三大数学思想在教学中的渗透，应遵循化繁为简的原则。以苏教版（2015年）五年级上册“用字母表示数”一课为例，其中两道例题完整地体现了抽象、推理、模型三大数学思想。

【例1】摆1个三角形用3根小棒；摆2个三角形用小棒的根数是2×3；摆3个三角形用的小棒根数是（ ）×3……三角形的个数和小棒的根数有什么关系？你能用一个式子表示吗？如果用a表示三角形的个数，小棒的根数是（ ）×（ ）。

【例2】甲乙两地之间的公路长280千米，一辆汽车从甲地开往乙地。你能用式子表示行驶了一段路程后剩下的千米数吗？已经行驶了50千米，剩下的千米数是280-（ ）；已经行驶了b千米，剩下的千米数是（ ）-（ ）。如果b=120，剩下多少千米？如果b=200呢？

一是抽象。两例中，不论是否已知要摆的三角形个数和行驶的路程，都可以用字母代表未知数，这是将确定与不确定，已知与未知简化和抽象的过程。

二是模型。学生需要从“摆三角形”“行路”等情境中抽象出三角形数与小棒数的关系、已行路程与剩下路程的关系，用语言表达这些关系，用含有字母的式子提炼这些关系，从而建立数学模型，体会和理解数学与外部世界的联系。

三是推理。推理发生在抽象与建立模型的过程中。例1中，从已知三角形个数时小棒的求法，推理出未知三角形个数时小棒的求法公式“a×3”，属于归纳推理；例2中，根据归纳推理得出的求剩下距离的公式“280-b”，进一步推理出行驶到120千米时，剩下160千米，属于演绎推理。在归纳与演绎的反复应用中，使学生初步领悟抽象与模型的数学思想。

二、深入分析，微观渗透

除了三大宏观数学思想，那些从微观上细分出来的各种多样化的数学思想方法也如影随形般地渗透在教材中，与数学知识、技能与各种实验活动紧密联系、融为一体。教师要在教材显性内容的背后，去挖掘、寻觅数学思想方法的“隐性支架”，让它发挥应有的作用。

如“小数数位顺序表”的教学。教师首先介绍小数点的“发明史”，让学生了解这个实心小圆点的来之不易。接着，引导学生对整数和小数部分进行分析、比较，使学生发现整数部分从最小计数单位“个”开始，以“满十进一”的方式不断叠加，直到无限，只有最小计数单位，没有最大计数单位；而小数部分从最大计数单位“十分之一”开始，以“退一作十”的方式不断细分，直到无限，只有最大计数单位，没有最小计数单位。无论是整数部分还是小数部分，每个数位都对应唯一的计数单位，数位确定了，计数单位也就唯一确定了……这样引导学生深入细致地观察、剖析与比较，从微观角度实现了数学中“对应”与“无穷”思想的渗透。

三、游戏渗透

为了避免学生对数学形成冰冷、枯燥、繁琐的刻板印象，教师可选择“亲民”游戏，让学生在活动或探究中发现数学思想方法。

如三年级上册“多彩的分数条”一课，教师首先组织折纸活动，让学生体会长短不一的分数条是怎样制作出来的，通过直观比较发现“1”被分割成越多份，得到的分数条越短，反之则越长。接着，通过“抢1”与“清零”游戏，让学生用分数条进行不同的排列组合，进一步观察比较，使常用分数单位之间、分数单位与“1”之间的关系生动起来，使学生对概念的理解更清晰而稳固，为“分数”在更高层次上的抽象奠定了基础。此后，教师又进一步提出：“还有一个神奇的‘1，它是用5个分数条拼成的，猜一猜可能是哪些分数？动手拼一拼。”学生尝试根据手中的分数条列举出可能的拼法，体验到了有序思考、分类思考的好处，感受到“替换”的神奇。此时，教师再追问：“如果跳出今天游戏里的分数，能不能用5个相同的分数条来铺成‘1？”如此循序渐进、拾阶而上的游戏设计，让学生“玩”得乐此不疲，也让数学思想方法在学生的指尖绽放。

四、数学史渗透

数学史中涉及的数学人物、事件、中外趣题或谜题等，包含着数学思想方法发展的历史，教师可结合教学内容适当渗透在教学中。

如五年级上册“认识小数”的教学中，学生很好奇“是谁发明了‘小数这种数？”，教师就在教学中穿插了十进制小数的发展历史，使学生了解到，现存最早关于小数思想的论述出现在我国古代数学家刘徽的《九章算术》里，记述了人们为什么需要“微小”的数，如何命名这种数，如何规定细分的原则等。这段故事也幫助学生认识到小数其实是“十进分数”的另一种表达方式，进一步体会了这种表达方式的简洁与便利，并由此打通整数部分与小数部分计数单位之间的内在关联，使数学思想方法的“化繁为简”“纳新入旧”“融旧于新”的神奇作用得以凸显。

数学史涉及的一些谜题常常更能激发学生的兴趣。教师可让学生在设定的故事情境中去探索未知，触摸数学思想方法的脉搏。如介绍“鸡兔同笼”“李白喝酒”“牛吃草”“百僧吃百馒头”“农民割草”等历史趣题，鼓励学生开放性地探究，尝试用多种途径、多元思考来解答同一问题。

五、实践活动渗透

教材安排的综合实践活动板块，其实质是引导学生从实际生活情境中抽象出数学问题，求解数学模型。在抽象与建模过程中，让学生经历和体验数学思想方法形成的过程。

如六年級上册“树叶中的比”一课。教师出示了一簇大小、颜色各不相同的银杏叶、春天的柳叶、四季常绿的松树叶……请学生从数学的角度去发现并提出问题。最后，学生的问题聚焦到“树叶的形状究竟与什么有关系？有怎样的关系？”并带着这个问题，进行了实际测量，通过收集、分析并比较数据，最终发现：树叶的形状与其长宽比有关，当这个比值接近时，无论它们是否来自同一棵树，形状都大致相似。学生从“不同的树叶”中发现了“相同之处”，也以自然、默会的方式习得了数学中“去异存同”的抽象思想。

六、梳理回顾渗透

要让学生“悟”到数学思想方法，教师还要在适当的时机引领学生进行知识的梳理与回顾，在比较、辨析与交流中，让思想凸显出来。

如在学过小数加减计算方法后，学生提出了这样的疑问：“10-1.23”为什么对不齐了？显然学生已获得的“整数加减法用竖式计算末尾总是对齐”的旧经验与新知识“小数加减法用竖式计算要把小数点对齐”发生了认知冲突。于是教师将小数加减法与整数加减法的竖式写在黑板上，引导学生通过观察、比较发现：无论整数加减法还是小数加减法，竖式计算时，相同数位上的数都是对齐的。如果把整数改写成小数，会发现整数加减法的末尾之所以能对齐，正是因为它的小数点始终对齐。如果把小数加减法中参加运算的两个小数改写成相同位数的小数，其末尾也是能对齐的，如“10-1.23”可以改写成“10.00-1.23”。研究并未就此结束，在认识到“小数点对齐”其实就是“相同数位对齐”的另一种表达方式之后，教师引导学生深入探究“为什么相同数位要对齐”，使学生进一步体会“同类计数单位的数，才能相加减”，有效建立整数、小数加减运算的模型[2]。

七、自省反思渗透

引导学生对自己答错的题进行自省反思，有利于促其感悟数学思想方法。如例3。

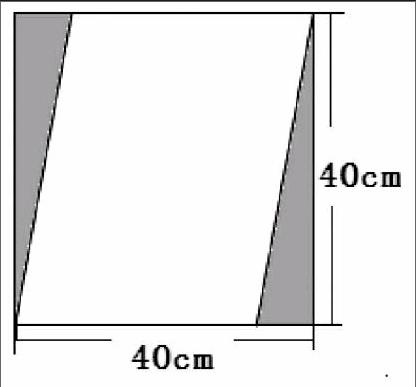
【例3】如图，正方形被分成了一个平行四边形和两个完全相同的三角形。已知一个三角形的面积比平行四边形的面积少700平方厘米，求三角形和平行四边形的面积。

有两位答错题目的学生作了如下反思。学生A：我要学会冷静地整理条件，如果把条件记录下来，就会发现“大白+小灰灰+小灰灰=1600；大白-小灰灰=700”。这样，就很容易想到用替换的方法来解题了。（“大白”和“小灰灰”分别是教师以电影人物命名的图中空白和阴影部分。）学生B：不要把简单的想复杂，其实只需要用替换的方法，把大平行四边形给替换成“三角形+700”，大正方形里去掉700就是3个三角形的面积了。可见，这两位学生已经能从数学思想方法的层面去评价自己，并改善自己的思维方式了。

综上所述，要让学生在做做游戏、听听故事、动手实践的过程中，激活并维持学习数学的动力系统，通过梳理回顾所学、自省反思自悟，提升数学思维品质，掌握数学思想方法，获得数学素养。

参考文献

[1]史宁中.数学思想概论[M].长春：东北师范大学出版社，2015.

[2]颜春红.渗透模型思想形成计算技能[J].小学教学设计，2015（2）：52.

（责任编辑 郭向和）