运载火箭故障检测序列优化

汪芊芊，蓝 鲲，王海涛

(北京宇航系统工程研究所，北京100076)

运载火箭故障检测序列优化

汪芊芊，蓝 鲲，王海涛

(北京宇航系统工程研究所，北京100076)

针对运载火箭故障检测序列优化这一新问题，建立数学模型并提出基于离散粒子群算法的故障检测序列优化方法。该算法通过测试集优化获得优选测试集，再通过检测序列优化对优选测试集中测试进行排序，获得优化的故障检测序列。最后以运载火箭时序控制系统为对象进行了验证，结果证明，基于离散粒子群算法的故障检测序列优化方法能够在保证故障状态全覆盖的前提下减少测试数量及成本，大大提高测试效率，且相较于遗传算法具有更好的优化性能和计算效率，适用于运载火箭故障检测序列优化。

故障检测序列； 离散粒子群； 测试性设计

0 引 言

面对当前运载火箭高密度、高效率、低成本的发射需求，如何合理安排测试项目及测试顺序，提高运载火箭的测试效率并降低测试成本，即测试序列优化[1]，成为运载火箭测试的重要课题。对于运载火箭来说，测试序列优化需解决两个问题：(1)故障检测序列优化，即以较低的测试成本对各个可能发生故障的状态进行测试覆盖；(2)故障隔离序列优化，即以较低的测试成本实现故障发生后的快速故障定位。

传统的测试序列优化多关注的是故障隔离序列优化[2-4]，而对于故障检测序列优化的研究较少。故障检测序列优化是约束优化问题，解决该类问题的方法目前主要有逆向的动态规划[5]、正向的启发式搜索[1,6-7]和进化算法[8-10]。对于故障检测序列优化来说，利用动态规划算法解决该问题具有O(n!)的计算复杂度，而运载火箭仅单个分系统测试项目就动辄数十项，因此难以利用动态规划算法或直接遍历来解决该问题；启发式搜索是一种局部的逐步优化“贪心算法”，易陷入局部最优，且需依靠回溯保证其优化性能，因此容易产生计算爆炸，不适用于大规模系统；而进化算法在全局样本空间内利用样本的迭代使当前解不断向最优解进化，如粒子群算法、遗传算法等，适用于约束条件较少的大范围寻优。本文选取进化算法中的离散粒子群算法(Discrete particle swarm optimization, DPSO)，提出了基于DPSO算法的运载火箭故障检测序列优化方法，并以时序控制系统的故障检测序列优化为例，验证了该方法的有效性。

1 故障检测序列优化问题分析与建模

1.1 问题提出

对于被测系统来说，其故障及测试信息可以用六元组(F,P,T,C,S,Ω)表示，其中：

F={f1,f2,f3,…,fm}是系统故障状态集合；

P={p(f1),p(f2),…,p(fm)}是系统各个故障fi的故障率集合；

T={t1,t2,…,tn}是系统的可选测试集；

C={c(t1),c(t2),…,c(tn)}是以时间、人力要求、测试难度等指标衡量的测试成本集合；

S={s1,s2,…,sl}是测试状态集，表示系统在测试过程中可能产生的状态；

Ω={F(t1),F(t2),…,F(tn)}是故障覆盖集，其中F(ti)表示测试ti所能检测到的故障集合。

故障检测序列优化包括两个方面：(1)测试集优化：利用优化算法对系统的可用测试集进行优选；(2)检测序列优化：对于优选测试集，依据测试状态、故障检测率等因素对优选的测试集进行排序，得到故障检测优化序列。

(1)测试集优化

定义故障检测覆盖率为被测试覆盖的故障数与总故障数的比值，即

(1)

式中：TS表示所选测试集。快速测试的基本前提是达到100%的故障检测覆盖率，以保证运载火箭无故障漏检。在此前提下，对系统可选测试集进行优化，以尽量减少测试成本及测试个数。构造检测集代价函数CTs为：

(2)

(3)

(2)检测序列优化

为确定测试实施策略，对(1)中所得的最优测试集进行检测序列优化。在测试实施过程中，总是希望尽早覆盖到可能发生故障的状态，以预留充分的时间进行故障诊断及系统修复；同时，各个测试的实施之间可能需要进行系统测试状态的转换，导致测试时间延长，且测试状态的频繁转换易导致系统故障。所以，测试排序需要遵循以下原则：

(a)优先进行故障检测率高的测试；

(b)尽量减少测试过程中的由于测试状态转换导致的测试成本。

C=K1×CFDR+K2×CSchange

(4)

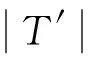
2 基于离散粒子群算法的故障检测序列优化方法

2.1 离散粒子群算法简介

离散粒子群算法由Kennedy等在1997年提出[12]，算法采用速度-位置模型，在允许范围内初始化一群随机粒子(潜在解)，每个粒子都有一个速度决定它们的飞行，在每一次迭代中通过跟踪两个极值来更新自己：粒子本身迄今为止所找到的个体极值Pbesti和整个种群迄今为止所找到的全局极值Gbesti。所有粒子的优劣由被优化函数所决定的适应度来衡量。粒子的速度和位置公式如下：

(5)

(6)

2.2 测试集优化

由离散粒子群算法的概念可知，离散粒子群算法利用粒子适应度函数来体现实际问题的优化需求，而粒子就是问题的潜在解。将测试集优化问题与离散粒子群算法结合，抽象出新的速度-位置模型如下：

(1)粒子位置：粒子位置表示测试集优化的潜在解，为使粒子形式一致且能够表示不同的测试集优化结果，将粒子位置定义为二进制向量xi=(xi1,xi2,…,xin)，n为可选测试项目的总数。xij表示第i个粒子是否选中第j个测试，是则为1，否则为0。xi的值按照式(6)更新。

(2)粒子速度：粒子速度将决定粒子下一次所在的位置，即测试集的优化方向。本文中将粒子速度定义为和粒子同维数的随机矩阵vi=(vi1,vi2,…,vin)。vij的值域为[0,1]，其值按式(5)更新。

(3)粒子适应度函数：粒子适应度值将决定粒子是否能被选中,对于测试集优化问题来说，如何把故障检测率、测试代价等因素融入粒子适应度函数，是构建粒子适应度函数需考虑的主要问题。结合式(2)所列测试集优化模型，构造适应度函数如下：

(7)

2.3 检测序列优化

检测序列优化也属于离散量优化，但由于组成序列的各个数值之间具有约束关系(序列中各个数值出现且仅出现一次)，因此无法直接应用传统的离散粒子群算法进行优化。文献[13]根据序列优化问题对粒子群算法的速度-位置模型进行了适应性改进，定义了新的粒子位置与速度更新公式如下：

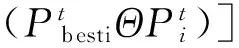
(8)

(9)

对于检测序列优化问题，抽象出粒子位置及速度模型如下：

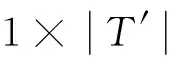
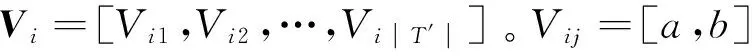
(3)适应度函数:根据检测序列优化的数学模型可知，测试成本函数C是检测序列优化目标，因此，将测试成本函数C作为适应度函数，即：

F(xi)=C=K1×CFDR+K2×CSchange

(10)

式中:序列xi的故障检测实施成本CFDR可根据式(4)唯一确定。但由于每个测试对应的测试状态不止1个，同一测试序列可能有多种状态转换方式，但总存在最低的状态转换成本。因此，设计CSchange的计算方法如下：

第一步：读取第1个测试的测试状态作为第1个测试的可行测试状态；

第二步：依次对各个测试判断其与前一个测试的最小状态转换成本，直至最后一个测试，具体步骤如下：

1)对测试序列中的第i个测试，读取其测试状态作为第i个测试的可行测试状态。i的初始值为2；

2)判断第i个测试与第i-1个测试是否有相同的可行测试状态，若有，则第i个测试与第i-1个测试间的最小状态转换成本为0，跳到第二步；否则， 跳到3)；

3)判断第i个测试与第i-1个测试间的最小状态转换成本，并根据该最小状态转换成本所对应的测试状态更新第i个测试和第i-1个测试的可行测试状态。

4)i=i+1，跳到1)，直至所有测试间的最小状态转换成本均得出；

第三步：根据式(4)计算状态转换成本CSchange。

2.4 故障检测序列优化方法步骤

基于离散粒子群算法的故障检测序列优化方法流程如图1所示。

3 实例校验及算法对比

3.1 实例校验

为验证该方法的有效性，以某运载火箭时序控制系统为对象进行故障检测序列优化。该时序控制系统共有26个故障状态，11个备选测试项目，5种测试状态。目前对于时序控制系统的测试多依据测试人员的经验进行。为保证故障状态全覆盖，一般会选取所有测试项目，并依据经验定性分析确定测试顺序，因而导致了较多的测试冗余及较高的测试成本。时序控制系统的故障-测试相关矩阵及测试与测试状态的对应关系如表1所示。考虑测试状态转换费用、难度、时间及人力成本等因素，定义各测试状态间的状态转换成本如表2所示：

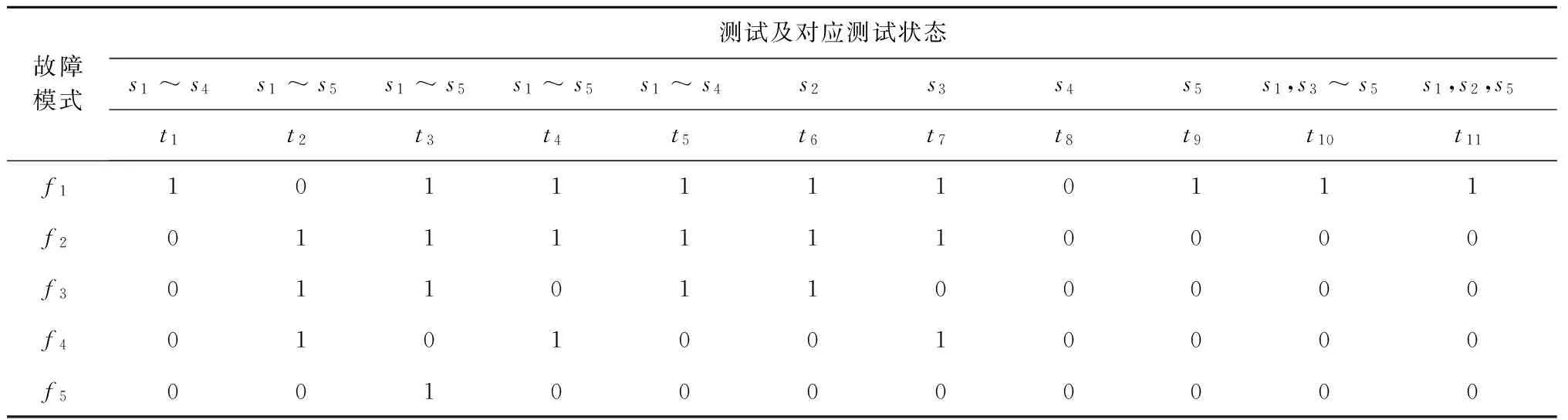
表1 时序控制系统的故障-测试相关矩阵Table 1 D-matrix of the timing sequencing control system

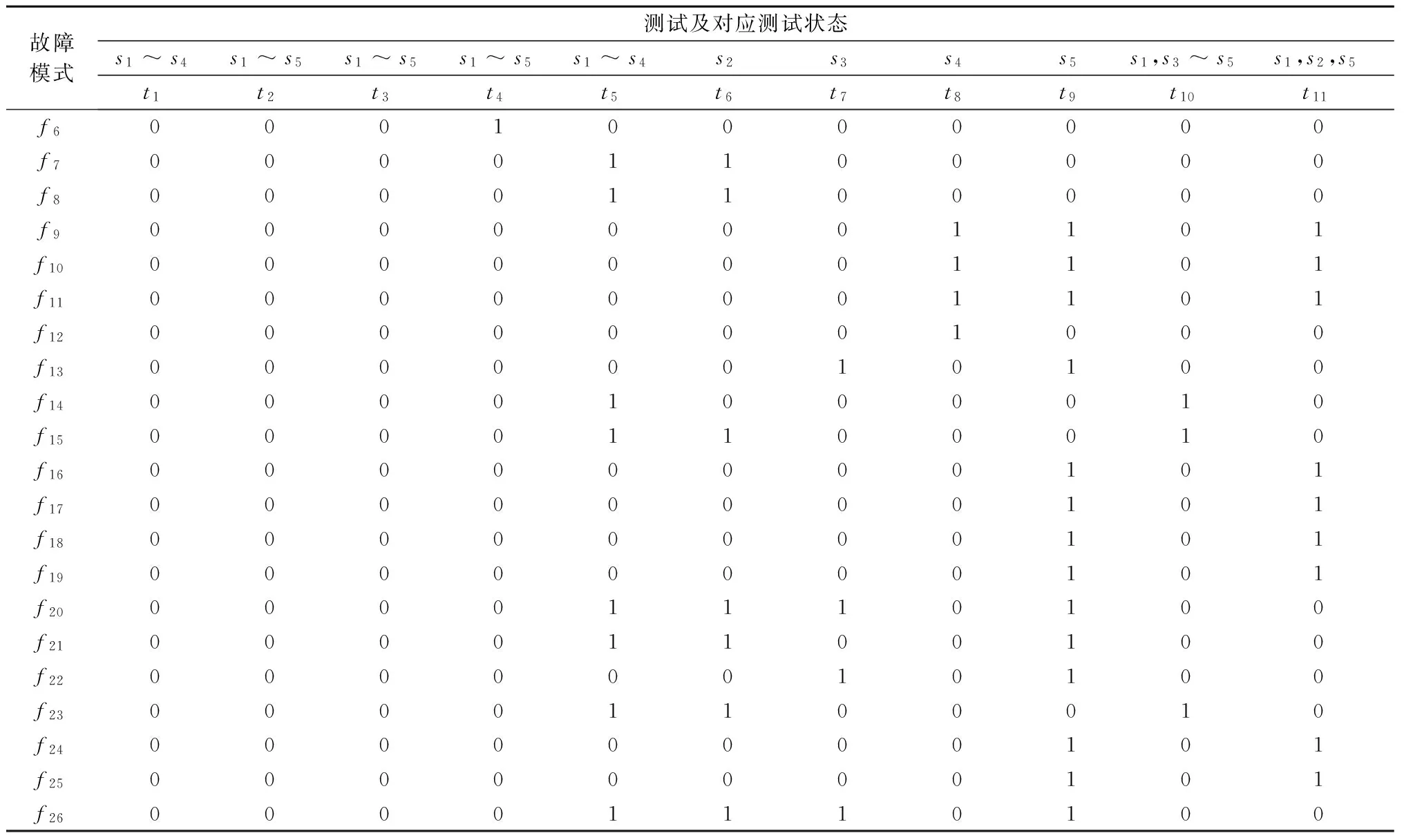
续表1

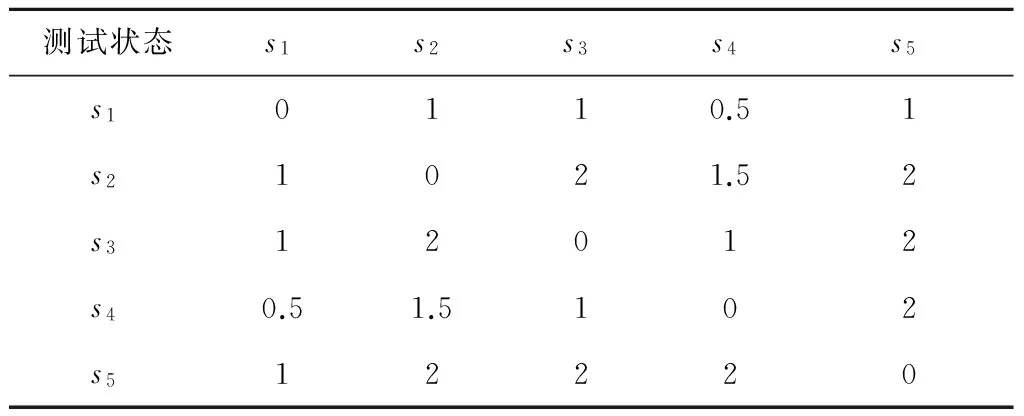
表2 各测试状态间的转换成本矩阵Table 2 Costs caused by conversions between test states

假设各个测试项目的成本均为1，各个故障状态的故障率相同，对时序控制系统进行故障检测序列优化。取粒子数M=10，迭代次数t=50，各权重系数K=10，K1=K2=1，运算结果如表3所示。

表3 时序控制系统故障检测序列优化结果Table 3 Optimization result of the timing sequence control system

注：原成本表示选取备选测试集中的11个测试并依顺序实施的成本。

由图2、图3离散粒子群最优适应度变化趋势图可以看出，在解决故障检测序列优化问题时，离散粒子群算法可以较快地收敛到最优适应度值，且收敛趋势稳定。通过优化的故障检测序列所得到的故障检测树如图4所示，T代表被当前测试覆盖到的故障，NT表示未被之前的所有测试覆盖到的故障。

根据以上优化结果可以发现：

(1)优化的快速测试集满足故障检测率γFD=100%，且将备选测试集中的11个测试缩减到5个测试，测试集成本降低为原成本的20.6%；

(2)优化的故障检测序列利用前两个测试即覆盖了85%的故障，并且合理规避了较高的状态转换成本，测试总成本降为原成本的23.6%，实现了快速低成本的测试。

3.1 算法对比分析

为验证基于离散粒子群算法的故障检测序列优化方法的有效性及优越性，将离散粒子群算法与遗传算法进行对比分析。仍以上述运载火箭时序控制系统为应用对象，在相同的仿真环境下，利用遗传算法进行故障检测序列优化。以测试集优化为例，取遗传算法的杂交概率为0.9，变异概率为0.04，离散粒子群算法的参数设置不变，在迭代次数均为50的条件下，分别对两种算法重复运行20次，比较两种算法性能差异，结果如表所示。

表4 算法性能对比Table 4 Comparison of tow algorithms

注：运行时间取20次重复运行的平均值，最优序列及最优适应度值取20次重复运行中出现次数最多的优化结果。

由表4可以看出，离散粒子群算法和遗传算法均可应用于测试集优化并能够收敛到某个优化解。但离散粒子群算法在种群数量达到10以上即可较稳定地寻得最优解，而遗传算法需要50以上。同时，在相同的种群规模及迭代次数下，离散粒子群算法的运行时间要短于遗传算法，约为遗传算法的60%。相较之下，离散粒子群算法能够更加快速有效地实现故障检测序列优化。

4 结 论

通过对基于离散粒子群算法的故障检测序列优化方法进行验证，可以发现：故障检测序列优化能够在保证故障测试全覆盖的前提下极大减少测试数量及测试代价，提高了运载火箭的测试效率。同时，基于离散粒子群算法的故障检测序列优化方法能够多维度考虑影响测试选择及实施顺序的因素，包括测试成本、测试的故障检测能力、测试状态转换等，对于运载火箭的故障检测序列优化可行有效，且具有通用性。

[1]PattipatiKR,AlexandridisM.Applicationofheuristicsearchandinformationtheorytosequentialfaultdiagnosis[J].IEEETransactionsonSMC, 1990, 20(4): 872-887.

[2] 于劲松，张帆，万九卿. 基于故障相关矩阵的最优测试序列生成方法[J]. 计算机测量与控制，2009, 17(6):1077-1083. [YuJin-song,ZhangFan,WanJiu-qing.Approachofoptimaldiagnosistreegenerationbasedondependencematrix[J].ComputerMeasurement&Control, 2009, 17(6):1077-1083.]

[3] 刘成瑞，张庆振，任章. 基于扩展故障树的运载火箭故障诊断专家系统[J]. 宇航学报，2008，29(6):1936-1941. [LiuCheng-rui,ZhangQing-zhen,RenZhang.Faultdiagnosisexpertsystemforlaunchvehiclebasedonaugmentedfaulttree[J].JournalofAstronautic, 2008, 29(6):1936-1941.]

[4] 景小宁，李全通，陈云翔，等. 基于信息熵的最少测试费用故障诊断策略[J]. 计算机应用，2005, 25(2):417-420. [JingXiao-ning,LiQuan-tong,ChenYun-xiang,etal.Informationentropy-basedfaultdiagnosisstrategywithleasttestcost[J].ComputerApplication, 2005, 25(2):417-420.]

[5]BertsekasDP.Dynamicprogramming:deterministicandstochasticmodels[M].EnglewoodCliff,NewJersey:Prentice-Hall, 1987.

[6] 黄以锋，景博，罗炳海，等. 基于Rollout算法的序贯多故障诊断策略[J]. 控制与决策，2015, 30(3):572-576. [HuangYi-feng,JingBo,LuoBing-hai,etal.Sequentialmultiplefaultdiagnosisstrategybasedonrolloutalgorithm[J].ControlandDesign, 2015, 30(3):572-576.]

[7] 杜敏杰，蔡金燕，刘利民. 基于分支定界-改进AO*算法的序贯测试策略优化[J]. 计算机测量与控制, 2012, 20(5): 1214-1218. [DuMin-jie,CaiJin-yan,LiuLi-min.Integrationofbranch-and-boundandmodifiedAO*algorithmforsequentialtestingstrategyoptimization[J].ComputerMeasurement&Control, 2012, 20(5): 1214-1218.]

[8] 蒋荣华，王厚军，龙兵. 基于离散粒子群算法的测试选择[J]. 电子测量与仪器学报，2008, 22(2):12-15. [JiangRong-hua,WangHou-jun,LongBing.Testselectionbasedonbinaryparticleswarmoptimization[J].JournalofElectronicMeasurementandInstrument, 2008, 22(2):12-15.]

[9] 蒋荣华，王厚军，龙兵. 基于DPSO的改进AO*算法在大型复杂电子系统最优序贯测试中的应用[J]. 计算机学报, 2008, 31(10):1835-1840. [JiangRong-hua,WangHou-jun,LongBing.ApplyingimprovedAO*basedonDPSOalgorithmintheoptimaltestsequencingproblemoflargescalecomplicatedelectricsystem[J].ChineseJournalofComputers, 2008, 31(10): 1835- 1840.]

[10] 丁昊. 基于多信号流图的系统测试性建模分析及软件设计[D]. 哈尔滨：哈尔滨工业大学, 2013. [DingHao.Modeling,analysisandsoftwaredesignforsystemtestabilitybasedonmulti-signalflowgraph[D].Harbin:HarbinInstituteofTechnology, 2013.]

[11]DebS,PattipatiKR.Multi-signalflowgraphs:anovelapproachforsystemtestabilityanalysisandfaultdiagnosis[J].IEEEAerospaceandElectronicSystemsMagazine, 1995, 10(5): 14-25.

[12]KennedyJ,EberhartRC.Adiscretebinaryversionoftheparticleswarmalgorithm[C].The3rdProceedingsoftheWorldMultiConferenceonSystemic,CyberneticsandInformatics,Piscataway,NJ,USA,June10-July13, 1997.

[13] 陈海彬，郭建文，孙振忠，等. 基于自适应变异粒子群优化算法的产品装配序列优化[J]. 组合机床与自动化加工技术, 2015, 7(7):153-156. [ChenHai-bin,GuoJian-wen,SunZhen-zhong,etal.Productassemblysequencesplanningbasedonadaptiveparticleswarm[J].ModularMachineTool&AutomaticManufacturingTechnique, 2015, 7(7):153-156.]

通信地址：北京市9200信箱10分箱9号(100076)

电话：18518921392

E-mial:lucky306@163.com

(编辑：张宇平)

Research on Optimal Test-Sequencing Problem for Fault Detection of Launch Vehicle

WANG Qian-qian, LAN Kun, WANG Hai-tao

(Beijing Institute of Astronautical System Engineering, Beijing 100076, China)

An algorithm based on discrete particle swarm optimization (DPSO) is proposed in this paper for the optimal test-sequencing for the fault detection of a launch vehicle. This algorithm optimizes the original test set first to obtain the optimal test set, and then optimizes the test sequence based on the optimal test set. A timing sequencing control system is taken as an example for modeling. The result shows that this algorithm not only reduces the quantity of the test sets and the test cost, but also performs much better than the genetic algorithm (GA) in the optimization results and computational efficiency.

Optimal test-sequencing problem for fault detection; Discrete particle swarm optimization; Design for testability

2016-07-29;

2017-02-09

装备预先研究项目"运载火箭快速测试与发射总体技术"(51320120301)

TH873.7

A

1000-1328(2017)04-0428-07

10.3873/j.issn.1000-1328.2017.04.013

汪芊芊(1992-)，女，硕士生，主要从事运载火箭测试性评估方面的研究。