具有终端角度约束的固定配平型再入弹头制导方法
周 军,葛振振,林 鹏
(西北工业大学精确制导与控制研究所,西安710072)
具有终端角度约束的固定配平型再入弹头制导方法
周 军,葛振振,林 鹏
(西北工业大学精确制导与控制研究所,西安710072)
针对固定配平型飞行器带终端角度约束的末制导问题,本文基于滚转制导与三维圆周制导,提出一种新颖的制导方法。首先,根据再入弹头与目标的相对几何关系以及终端角度约束,在三维空间内确定出唯一的圆轨迹。然后,通过滚转制导控制升力方向使实际速度方向与期望速度方向重合后,弹头将沿圆轨迹命中目标,并满足终端角度约束。此外,为增强制导方法的鲁棒性,引入干扰观测器对干扰进行实时观测与补偿,并采用变结构控制理论进行制导律设计。仿真结果表明:该制导方法具有较高的命中精度,同时也能满足终端角度约束,并具有较强的鲁棒性。
固定配平;再入弹头;终端角度约束;滚转制导;圆周制导;干扰观测器
0 引 言
随着各类反导武器的不断发展,对弹道导弹的突防能力提出了越来越高的要求。机动弹头在与弹体分离后,可根据需要改变飞行弹道,通过末制导系统来提高命中精度。
文献[1]介绍了可实现再入机动的3种基本构造型式,它们分别是十字翼型、倾斜-转弯型和固定配平型,其中固定配平控制型式具有单轴控制特性,仅有一个控制轴(滚转轴)和一个大小不可调节的升力矢量,通过改变滚转角进行机动。
固定配平型的再入飞行器最早应用在飞船和空天返回式运载器上,例如Gemini和Apollo太空船。它们一般采用标称轨迹法,这种方法的落点控制精度不高,但能满足飞船再入的要求。固定配平外形再入弹头最典型代表是美国的MK500逃逸型机动弹头,其通过弯头锥的外形产生固定配平攻角,控制滚动实现机动,但它是按预定程序飞行,降低一定精度以保证机动能力。
目前,国内外关于固定配平控制型式飞行器制导控制技术的可查阅文献十分有限。文献[1]给出了叉积制导律,但其没有解决接近目标时升力多余问题,导致落点精度不高;Gracey等[2]针对文献[1]提出的制导律进行改进得到一种针对固定配平控制型式飞行器更加有效的滚转制导律,具有较高的命中精度;Bibeau等[3]采用直接配点法与非线性规划进行轨迹规划,多次在线快速重新规划轨迹,但该方法通常用于飞行时间远大于轨迹规划所需时间的场合;李自行等[4-5]将文献[2]提出的滚转制导应用于固定配平型再入机动弹头,并分别研究喷流和变质心控制方式对滚转通道的控制。
此外,对常规制导武器而言,制导系统的主要目的是产生合适的制导指令使末端脱靶量为零。然而在一些特殊情况下,不仅期望机动弹头落地时能获得最小脱靶量,还能以一定的姿态命中目标,从而最大限度地发挥战斗部效能,取得最佳毁伤效果。这就对导引任务的实现增加了终端角度约束[6]。
自文献[7]首次在机动弹头再入制导研究中引入落角约束以来,许多学者根据不同的理论方法提出了多种具有终端角度约束的制导律。文献[8-9]分别利用最优控制和变结构控制设计含落角约束的制导律。此外还有偏置比例导引律[10-11]、几何曲线导引律以及复合制导等[6]。Manchester等[12]根据平面弹道的几何特性提出了一种具有终端角度约束的三维圆周导引律[13-14]。此外,文献[11-15]分别采用偏置比例导引和开关制导律实现落角约束,并在导引律设计过程中还考虑了飞行中的导引头视场角约束。针对制导武器末端攻击角约束和弹道尽可能平直的要求,文献[16]应用有限时间控制方法,设计了具有末端攻击角约束的连续有限时间稳定制导律,使闭环制导系统在有限时间内视线角速度收敛到零和视线角收敛到期望值。文献[17]将多约束下的制导问题转化为具有控制饱和的线性系统的镇定问题,基于参量Lyapunov方程的低增益反馈方法,推导出带低增益参数的纵向自适应制导律。但上述方法均以十字翼型、倾斜-转弯型飞行器为研究对象,无法应用于具有单轴控制特性(仅升力方向可控)的固定配平型飞行器。
针对固定配平型再入飞行器,文献[2]所提出的滚转制导不能解决终端角度约束问题。本文将滚转制导与三维圆周制导相结合,提出一种新颖的制导方法,并引入干扰观测器对系统干扰和不确定项进行估计补偿,同时采用变结构控制设计制导律,进一步提高系统的稳定性和鲁棒性。
1 问题描述与分析
1.1 坐标系定义及模型建立
如图1所示,M为再入弹头质心位置,T为目标位置。
1) 目标坐标系T-xyz
原点T为目标位置,Ty轴沿当地铅垂线方向(指向上为正),Tx轴在当地水平面内且与Ty垂直(指向再入飞行器末制导初始时刻运动方向为正),Tz轴与上述两轴垂直并构成右手坐标系。
2) 弹道坐标系O1-x2y2z2
原点O1为弹头位置,O1x2轴沿再入弹头速度方向,O1y2轴在在包含目标坐标系Ty轴的铅垂面内且与O1x2垂直(指向上为正),O1z2轴与上述两轴垂直并构成右手坐标系。
由于末制导时间较短以及本文主要研究针对固定目标的含终端角约束的制导律,因此忽略地球自转的影响,可将目标坐标系作为惯性系。
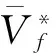
R=xi+yj+zk
(1)
(2)
(3)
根据上述坐标系的定义建立固定配平型式再入机动弹头的质心动力学和运动学方程[18]:
(4)
(5)
(6)
(7)
(8)
(9)
式中:VM为弹头的速度大小;m为弹头质量;D、L分别为阻力、升力;g为重力加速度;γ、φ、σ分别为航迹角、航向角、速度倾侧角;x、y、z分别为位置矢量R沿目标坐标系各轴分量。
式中:CD、CL分别为阻力、升力系数;ρ为大气密度;S为参考面积。
1.2 三维圆周导引分析
根据上述坐标系的定义可以将其具有终端碰撞角度约束的末制导问题描述为[14]:通过控制再入弹头的速度倾侧角σ,改变速度方向,使其在命中目标时刻tf,同时满足以下等式:
R(tf)=0
(10)
(11)
(12)
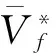
圆轨迹MST的含义为:假定再入弹头沿该圆轨迹飞行,则可以保证在命中目标时刻tf同时满足式(10)~(12)。
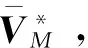
a. 使误差角η逐渐减小为0;
b. 满足η=0以后,保持η≡0,则弹头沿含终端角度约束的圆轨迹命中目标。
2 三维圆周制导律设计
2.1 圆周制导模型
定义速度误差坐标系O1-xeyeze,如图2所示。
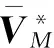
设目标坐标系T-xyz与速度误差坐标系O1-xeyeze之间的转换矩阵为Le:先绕y轴正向旋转φ角,然后绕z′轴正向旋转γ角,最后绕O1xe轴正向旋转ξ角,即按2-3-1次序旋转。
[xeyeze]T=Le[xyz]T
(13)
[cosη0sinη]T
(14)
根据绝对导数与相对导数之间的关系,可得
(15)
(16)
(17)
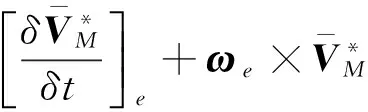
(18)
-[cosqαcosqβsinqα-cosqαsinqβ]T
(19)
式中:qα、qβ分别为弹目视线高低角和方位角。
(20)
(21)
(22)
联立式(15)、(18)、(21)和(22),可得:
(23)
将式(5)、式(6)代入式(23)中,并考虑实际飞行过程中的气动系数不确定性与外界环境干扰等因素的影响,可得三维圆周制导模型:
(24)
式中:L0为标称升力;d为气动系数不确定性、外界环境干扰等因素所引起的干扰项。
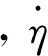
2.2 干扰观测器
为提高制导系统的抗干扰能力,本文引入干扰观测器[19-22]对干扰项d进行实时估计,并利用干扰估计值进行补偿,从而增强系统的鲁棒性。
还真是报应,我在前一秒对那个女孩表示了鄙视之后,下一秒就看到那个和她眉目传情的家伙就是,我的男朋友,秦明。不过已经无所谓,因为下一刻,他就会被我称作,前男友。我在最后一刻还是犯了所有小女人都犯的矫情的毛病——我要和他在我们最初见面的地方说分手。
假设式(24)中除了干扰项d未知之外,其它均为已知项,因此定义f0为全部已知项的总和,即
(25)
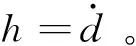
(26)
针对系统(26)所设计的观测器为:
(27)
式中:e1=z1-x1;β1,β2为观测器参数。
定义观测误差向量为:
E=[e1,e2]T
式中:e2=z2-x2为干扰项d的观测误差。
联立式(26)和式(27),可得
(28)
式中:
引理1[22].如果式(28)中的矩阵A的特征值均为负实数,并且至少满足以下所列条件中的一条:
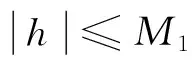
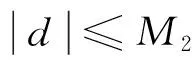
上述所设计的干扰观测器需要按照引理1选取干扰观测器参数β1和β2使得式(28)中的矩阵A的特征根均为负实数。在满足上述条件下,可保证干扰的观测误差e2渐近收敛到零点附近任意小的有界邻域内,但不同的β1和β2,其干扰观测误差的收敛速度和收敛误差存在差异。
通常情况下,闭环系统对干扰观测器的收敛速度和收敛误差存在一定的要求,一般要求收敛速度快、收敛误差小。因此在实际中,干扰观测器参数的选取除满足引理1之外,还和干扰变化快慢有关。若在干扰观测器参数相同的情况下,则干扰变化越快,观测误差的收敛速度越慢、收敛误差越大;若在干扰变化相同的情况下,则矩阵A的特征根离原点越远(复平面原点左侧),观测误差的收敛速度越快、收敛误差越小。所以应该在满足引理1的前提下,根据系统干扰变化快慢和对观测误差收敛速度、误差的要求,选取合适的观测器参数。
2.3 制导律设计及稳定性证明
设计相应的制导律使误差角η逐渐减小为0,并保持η≡0。针对制导模型式(24),采用变结构控制理论设计的制导律为:
f0=-kη-w·sgn(η)-z2
(29)
式中:k,w为制导系数,取值为正;z2为干扰d的观测值;sgn(·)为符号函数。
本文采用的变结构控制律同样具有鲁棒性,可以有效的抑制干扰,但是当干扰较大且无干扰实时估计补偿的情况下,制导系数w的取值较大会使闭环系统在平衡点附近出现高频抖动。通过引入干扰观测器对干扰进行实时估计补偿,减小变结构控制律所引起的颤振。
引理2[23-24].考虑系统
(30)
定理1.对于系统(24),若下述条件(1)~(4)成立
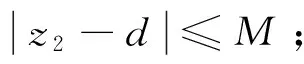
(2)k>0且w>M;
(3)VM>0;
(4) 式(29)成立。
证.
联立式(24)、式(25)和式(29),可得
(31)
则
(32)
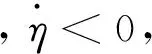
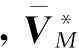
(33)
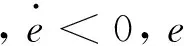
在η=0的情况下,根据几何关系可知
(34)
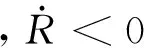
证毕.
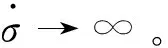
假设干扰d的上界为Md,即|d|≤Md,如果无干扰观测器进行干扰实时估计补偿,需满足w>Md以保证闭环系统的稳定性。但是,如果w取值较大,会引起系统在平衡点附近出现高频抖动。引入干扰观测器进行干扰实时估计补偿的情况后,仅需满足定理1中条件1和2即可保证闭环系统的稳定性。通过选取合适的干扰观测器参数β1和β2,可使M< 上述分析证明结果是以式(29)成立为前提,定义χ为 (35) 综上所述,结合式(29)和式(35)可得制导指令σ的计算公式 (36) 分别在标称情况下和存在不确定干扰情况下进行数学仿真,并对仿真结果进行分析。仿真参数:再入弹头质量m=400kg,阻力系数CD=0.2,升力系数CL=0.5,参考面积S=0.524m2。制导参数:k=1.5,w=0.002,β1=10,β2=160。k和w影响命中精度和落角约束,其取值应满足定理1,k和w的取值越大,命中精度越高、落速越大、落角误差越小。β1和β2主要影响观测误差的收敛速度和误差,并影响w下界,其取值应满足引理1。β1和β2的取值越大,观测误差的收敛速度越快、收敛误差越小,w下界越小。 (1) 标称情况下 选取4组仿真算例,各算例的初始条件和终端位置条件相同,但理想终端角度约束不同,见表1。 表1 初始与理想终端条件Table 1 Initial and desired final condition of vehicle (2) 存在干扰情况下 考虑在质量系数偏差、大气密度偏差、阻力系数偏差和升力系数偏差条件的综合作用下,分别对算例1~4进行100次蒙特卡罗打靶仿真,并对仿真结果进行统计分析。在蒙特卡罗仿真过程中,各偏差条件的取值范围为:质量系数偏差取值范围∈[-2%,2%];大气密度偏差取值范围∈[-10%,10%];阻力系数偏差取值范围∈[-10%,10%];升力系数偏差取值范围∈[-10%,10%]。各算例的落点分布如图4所示,蒙特卡罗仿真统计结果见表3。 表2 标称条件下终端状态误差Table 2 Final states error on nominal condition 表3 蒙特卡罗仿真统计结果Table 3 Statistical results of Monte-Carlo simulation 通过对在标称情况下以及存在干扰下的蒙特卡罗仿真结果分析可知:本文针对固定配平型再入弹头带终端角度约束的末制导问题所研究的新颖制导方法具有较高的命中精度,同时也能满足终端角度约束,并且具有较强的鲁棒性。 本文以固定配平型再入弹头为研究对象,其具有升力大小不可主动调节,仅升力方向可控的飞行特点。针对固定配平型再入弹头带终端角度约束的末制导问题,本文将滚转制导律与三维圆周制导律相结合,提出一种新颖的的制导方法,并采用干扰观测器和变结构控制律以增强制导系统的鲁棒性。通过在标称以及存在干扰和参数不确定情况下的数值仿真验证了该方法具有较高的命中精度,同时也能满足终端角度约束,具有较强的鲁棒性。文中给出的仿真实例说明了该方法的有效性。 [1]PageJA,RogersRO.Guidanceandcontrolofmaneuveringreentryvehicles[C].IEEEConferenceonDecisionandControl,California, 1977. [2]GraceyC,CliffEM,LutzeFH,etal.Fixed-trimre-entryguidanceanalysis[J].JournalofGuidanceControlandDynamics, 1982, 5(6): 558-563. [3]BibeauRT,RubensteinDS.TrajectoryoptimizationforAfixed-trimreentryvehicleusingdirectcollocationandnonlinearprogramming[C].AIAAGuidanceNavigationandControlConferenceandExhibit,Denver, 2000. [4] 李自行, 李高风. 一种基于不对称再入体的制导与控制方法研究[J]. 航天控制, 2011, 29(6): 44-53. [LiZi-xing,LiGao-feng.Researchonarollingguidancelawofasymmetricreentryvehicle[J].AerospaceControl, 2011, 29(6): 44-53.] [5] 李自行, 李高风. 一种基于固定配平的飞行器滚转制导律研究[J]. 空间控制技术与应用, 2012, 38(6): 23-49. [LiZi-xing,LiGao-feng.Avehiclerolling-guidancelawbasedonfixedtrimmedangleofattack[J].AerospaceControlandApplication, 2012, 38(6): 23-49.] [6] 蔡洪, 胡正东, 曹渊. 具有终端角度约束的导引律综述[J]. 宇航学报, 2010, 31(2): 315-323. [CaiHong,HuZheng-dong,CaoYuan.Asurveyofguidancelawwithterminalimpactangleconstraints[J].JournalofAstronautics, 2010, 31(2): 315-323.] [7]KimM,GriderKV.Terminalguidanceforimpactattitudeangleconstrainedflighttrajectories[J].IEEETransactionsonAerospaceandElectronicSystems, 1973, 9(6): 852-859. [8]XuXY,CaiYL.Optimalguidancelawandcontrolofimpactangleforthekineticvehicle[J],JournalofAerospaceEngineering, 2011, 225(9):. 1027-1036. [9] 胡正东, 曹源, 蔡洪. 带落角约束的再入机动弹头的变结构导引律[J]. 系统工程与电子技术, 2009, 31(2): 393-398. [HuZheng-dong,CaoYuan,CaiHong.Variablestructureguidancelawofreentrymaneuveringwarheadwithterminalangularconstraint[J].SystemsEngineeringandElectronics, 2009, 31(2): 393-398.] [10]YanL,ZhaoJG,ShenHR,etal.Three-demensionalunitedbiasedproportionalnavigationlawforinterceptionofmaneuveringtargetswithangularconstraint[J]JournalofAerospaceEngineering, 2015, 229(6): 1013-1024. [11] 黄诘, 张友安, 刘永新. 一种有撞击角和视场角约束的运动目标的偏置比例导引算法[J]. 宇航学报, 2016, 37(2): 195-202. [HuangJie,ZhangYou-an,LiuYong-xin.Abiasedproportionalguidancealgorithmformovingtargetwithimpactangleandfield-of-viewconstraints[J].JournalofAstronautics, 2016, 37(2): 195-202.] [12]ManchesterIR,SavkinAV.Circularnavigationguidancelawforprecisionmissile/targetengagement[J].JournalofGuidanceControlandDynamics, 2006, 29(2): 314 - 320. [13]YoonMG.Relativecircularnavigationguidanceforthree-dimensionalimpactanglecontrolproblem[J].JournalofAerospaceEngineering, 2010, 23(4): 300-308. [14] 胡锡精, 黄雪梅. 具有落点和落角约束的圆轨迹制导律[J]. 宇航学报, 2012, 33(5): 562-569. [HuXi-jing,HuangXue-mei.Circulartrajectoryguidancelawwithterminalconstraintsofimpactpointandimpactangle[J].JournalofAstronautics, 2012, 33(5): 562-569.][15] 顾家立, 陈万春. 一种带有导引头视角和落角约束的导引方法[J]. 宇航学报, 2013, 34(6): 782-787. [GuJia-li,ChenWan-chun.Homingguidancewithlockangleandimpactangleconstraints[J].JournalofAstronautics, 2013, 34(6): 782-787.] [16] 刁兆师, 单家元. 带末端攻击角约束连续有限时间稳定制导律[J]. 宇航学报, 2014, 35(10): 1141-1149. [DiaoZhao-shi,ShanJia-yuan.Continuousfinite-timestabilizationguidancelawforterminalimpactangleconstrainedflighttrajectory[J].JournalofAstronautics, 2014, 35(10): 1141-1149.] [17] 董晨, 晁涛, 王松艳, 等. 多约束下考虑控制饱和的自适应末制导方法[J]. 宇航学报, 2014, 35(6): 677-684. [DongChen,ZhaoTao,WangSong-yan,etal.Adaptiveterminalguidancewithcontrolsaturationundermultipleconstraints[J].JournalofAstronautics, 2014, 35(6): 677-684.] [18] 赵汉元. 飞行器再入动力学和制导[M]. 长沙: 国防科技大学出版社, 1997. [19] 韩京清. 自抗扰控制技术:估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2008. [20]GodboleAA,LibinTR,TaloleSE.Extendedstateobserver-basedrobustpitchautopilotdesignfortacticalmissiles[J].JournalofAerospaceEngineering, 2012, 226(12): 1482-1501. [21]LiSH,YangJ.Robustautopilotdesignforbank-to-turnmissilesusingdisturbanceobservers[J].IEEETransactionsonAerospaceandElectronicSystems, 2013, 49(1): 558-579. [22]YangXX,HuangY.Capabilitiesofextendedstateobserverforestimatinguncertainties[C]. 2009AmericanControlConference,St.Louis, 2009. [23]IsidoriA.Nonlinearcontrolsystems[M], 3rded.Springer-Verlag,London, 1995. [24]SunHF,YangZL,ZengJP.Newtracking-controlstrategyforairbreathinghypersonicvehicles[J].JournalofGuidance,Control,andDynamics, 2013, 36(3): 846-859. 通信地址:西北工业大学航天学院234信箱(710072) E-mail:zhoujun@nwpu.edu.cn 葛振振(1989-),男,博士生,主要从事制导控制理论及应用研究。本文通信作者。 通信地址:西北工业大学航天学院234信箱(710072) E-mail:gezhenzhen@126.com (编辑:张宇平) Terminal Guidance Law with Impact Angle Constraint for the Fixed-Trim Reentry Warhead ZHOU Jun, GE Zhen-zhen, LIN Peng (Institute of Precision Guidance and Control, Northwestern Polytechnical University, Xi’an 710072, China) As the fixed-trim reentry warhead only has a single axis of rolling control, a novel terminal guidance law with impact angle constraint is proposed in this paper. The three-dimensional terminal guidance law combines the traditional circular navigation guidance approach with impact angle constraint and the improved cross-product guidance method without impact angle constraint for fixed-trim warheads. According to the theoretical analysis, it has been proved that the new guidance law will guarantee zero miss distance and impact angle constraint by choosing proper guidance parameters. For improving the robustness of the guidance law, a linear disturbance observer is combined with the variable structure control to estimate the system uncertainties and disturbances during flight. Simulation results show that the proposed terminal guidance law can satisfy both miss distance requirement and impact angle constraint perfectly. Fixed-trim; Reentry warhead; Impact angle constraint; Cross-product guidance; Circular navigation guidance; Disturbance observer 2016-09-02; 2017-02-13 V448.2 A 1000-1328(2017)04-0375-09 10.3873/j.issn.1000-1328.2017.04.007 周 军(1966-),男,教授,博士生导师,主要从事先进控制理论及应用、导弹精确制导与控制技术、航天器控制与仿真技术等研究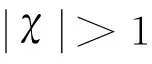
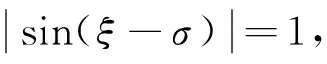
3 仿真校验
4 结 论

