求解中途飞越燃料最优转移轨道的同伦方法

潘 迅，泮斌峰，唐 硕

(1. 西北工业大学航天学院，西安710072；2. 航天飞行动力学技术重点实验室，西安 710072)

求解中途飞越燃料最优转移轨道的同伦方法

潘 迅1,2，泮斌峰1,2，唐 硕1

(1. 西北工业大学航天学院，西安710072；2. 航天飞行动力学技术重点实验室，西安 710072)

提出一种新的同伦方法，用于求解深空探测中对其他天体进行中途飞越的小推力燃料最优转移轨道，克服由于其存在内点约束及不连续Bang-Bang控制所导致的数值优化方法的求解困难。该同伦方法将同伦参数同时嵌入到性能指标和内点约束方程中，将容易求解的无内点约束且控制量连续变化的最优控制问题作为初始问题，求解一系列同伦参数递增所对应的同伦迭代子问题，直到得到原问题的解。该方法能够有效地解决中途飞越所导致的优化变量增加、求解难度增大等难题，能够快速、稳定地求解考虑中途飞越的小推力燃料最优转移轨道。最后，以地球到火星交会并中途飞越小行星和地球到木星交会并中途飞越火星两个任务为例进行数值仿真验证该同伦方法在求解中途飞越的燃料最优问题中的有效性和优越性。

中途飞越；最优控制；燃料最优；小推力；同伦方法；深空探测

0 引 言

深空探测是21世纪航天领域的一大热点。从经济性角度出发，多任务、多目标深空探测能够在节省经费的同时获得更多的科学回报。与单目标探测的航天任务相比，多目标探测任务对转移轨道设计提出了新的要求。

对天体的探测方式包括飞越、交会或撞击目标天体。对于多目标探测任务，对其中部分天体进行飞越是较为合理的探测方式。文献[1]对脉冲推进的航天任务，提出基于牛顿算法的多次中途飞越任务的转移轨道优化方法，利用该方法能使Galileo探测器完成多达11次中途飞越，从而对多个目标天体进行探测；文献[2]分析Deep Space探测器对Hartley完成两次飞越后，通过对剩余燃料进行合理规划，对小行星2002 GT进行飞越的任务设计；文献[3]研究航天器通过脉冲推进对火星进行飞越，然后跟随火星运行半圈，最后通过脉冲飞越火星返回地球。我国的嫦娥2号任务在完成对月探测后，也对小行星进行了飞越探测。文献[4]针对嫦娥二号从日地系L2点Lissajous轨道到Toutatis飞越的转移轨道进行设计研究；文献[5]研究嫦娥二号在实现对4179小行星飞越之后，利用剩余燃料选取小行星1997XF11和2005VS作为飞越探测目标的任务设计。

随着发动机技术的发展，小推力发动机具有比冲大、控制精度高等优点，能极大地提高探测器的有效载荷的比重，因此利用小推力发动机进行深空探测将是未来的发展趋势。然而小推力发动机推力小，持续时间长，燃料最优转移轨道分为推进段和滑行段，在发动机开关机点推力大小存在阶跃变化，因此在求解过程中存在较大困难。文献[6]研究了基于不变流形理论和Gauss伪谱法的日-地系Halo轨道到日-火系Halo轨道的小推力转移；文献[7]综述了当前轨道优化设计领域的常用方法，针对连续小推力作用下的深空探测任务轨道优化方法，对比和分析各方法的优缺点；文献[8]采用六次多项式形状逼近策略，并结合改进微分进化算法进行小推力行星借力转移轨道的初始设计；文献[9]结合我国即将开展的小行星探测任务，给出多目标、多任务小行星探测的一种推荐方案，分析得到6个可能的目标小行星，并对可行方案进行电推进转移轨道设计；文献[10]推导了包含时变内点约束的分块伪谱法，并对地球出发-小行星飞越-地球返回的小推力转移轨道进行设计；文献[11] 通过间接法对包含引力辅助的燃料最优小推力转移轨道进行研究，利用粒子群算法选取初值，利用同伦算法和开关函数检测法克服Bang-Bang控制的困难。

对于考虑中途飞越的航天任务的转移轨道，由于存在内点约束，其在优化过程中引入多个对应于约束条件的拉格朗日乘子，增加了打靶所需求解的变量，从而导致求解难度增加。虽然文献[8-11]能优化得到满足要求的转移轨道，但在优化过程中优化变量较多，需要结合微分进化算法，粒子群法等其他数值算法，计算过程较为复杂。本文提出一种新的同伦方法，先求解不包含内点约束的转移轨道，在该轨道上选取合适位置作为初始中途飞越点，从而在同伦初始时刻消除内点约束所产生的影响；然后通过对飞越点位置进行同伦，进而得到对目标天体进行中途飞越的转移轨道；同时对性能指标进行同伦，从而克服燃料最优问题Bang-Bang控制所导致的求解困难。

1 中途飞越的最优化问题

在进行航天器轨道初步设计时，不考虑其他天体引力、太阳光压以及其他摄动力，即假设航天器在中心引力场中运动，仅受到中心天体的引力作用和发动机推力作用，则航天器的动力学方程为

(1)

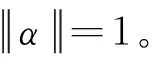
为方便计算以及保证计算精度，通常需要对动力学方程中的变量进行无量纲化。在日心黄道坐标系中，长度量、时间量和质量分别以AU(1AU=149597870700m)、a(1a=365.25d)、航天器初始质量m0进行无量纲化，太阳引力系数无量纲化后为39.476926AU3/a，同时需要对Tmax、Isp和g0进行无量纲化[9]。

对于中途飞越问题，除了在初始时刻和终端时刻存在约束外，在航天器进行中途飞越时刻也存在约束，即内点约束

r(tm)-rO(tm)=0

(2)

式中：tm为中途飞越时刻，rO表示中途飞越目标天体的位置矢量。

将端点约束和内点约束表示成p维的等式约束

φ(x(t0),x(tf),x(tm),t0,tf,tm)=0

(3)

式中:x=[r,v,m]T表示状态量，t0和tf分别表示初始时刻和结束时刻。

对轨道设计问题，优化的性能指标通常分为三种：时间最优，能量最优和燃料最优，都只与推力大小u有关，与推力方向α无关，因此，可将性能指标表示为

(4)

根据庞德里亚金极小值原理，通过引入拉格朗日乘子构造广义指标Jm和哈密尔顿函数H，可得

(5)

(6)

对于控制无约束的情况，广义指标的一阶变分为零是性能指标取得极值的一阶必要条件。通过对广义指标求一阶变分，可得协态方程为

(7)

根据最优控制理论，初始状态和终端状态的横截条件为[12]

(8)

内点约束时刻前后瞬时状态约束对应的横截条件为

(9)

内点约束时刻的静态条件为

(10)

式中：vO为中途飞越目标天体的速度矢量。

根据最优控制理论，可推导得到最优推力方向为

(11)

在推导推力大小u的最优控制律时，需要考虑不同性能指标的影响。在此，分别对性能指标为能量最优和燃料最优时的推力大小最优控制律进行推导：

1)当性能指标为能量最优时，其最小化性能指标可以表示成

(12)

将其代入到哈密尔顿函数，并对u求偏导，可得

(13)

为使哈密尔顿函数取得极小值，可得推力大小的最优控制律为

(14)

式中：S为开关函数，其表达式为

(15)

2)当性能指标为燃料最优时，其最小化性能指标可以表示成

(16)

同理可得其最优控制律为

(17)

当S=0时，最优推力大小不能确定，此时存在奇异控制。由于开关函数S连续变化，不会在某一时间区间内恒等于零，只会在有限孤立点处为零，因此可以不考虑S=0的情况。

推导得到推力方向和推力大小的最优控制律后，则将轨道优化问题转换为两点边值问题。对于无飞越的轨道转移，其终端约束为航天器位置速度与目标天体的位置速度一致，且不存在内点约束，则该打靶问题为7维问题，打靶变量为初始时刻的协态变量[λr(t0),λv(t0),λm(t0)]，打靶约束条件为

(18)

对于存在中途飞越的轨道转移问题，在中途飞越时刻，航天器位置与飞越天体位置一致，即每个中途飞越对应三个约束条件，同时由于中途飞越时刻tm未知，则该问题为十一维的打靶问题，打靶变量为[λr(t0),λv(t0),λm(t0),χ,tm]，打靶方程为式(2)，式(18)和式(10)，共11个等式约束，式(9)用于协态变量λr在tm时刻的更新。通过对该打靶问题进行求解，则可得到满足条件的转移轨道。

2 同伦方法

对于燃料最优转移轨道，从式(17)可知，其推力值u为Bang-Bang控制。由于其推力大小存在突变，利用间接法对其进行求解过程中存在很大困难，因此通常先求解得到能量最优转移轨道，通过对性能指标进行能量最优到燃料最优的同伦迭代，最终得到燃料最优转移轨道[11]。但在考虑中途飞越问题时，由于内点约束所带来的在飞越时刻协态变量和哈密尔顿函数的不连续等问题，上述同伦方法则难以适用。本文针对这一问题，提出一种新的同伦方法进行求解。

2.1 中途飞越内点约束方程的同伦

考虑初始时刻和终端时刻的状态量都给定的问题，端点约束对状态量的偏导数为零，因此不需要对端点约束对应的拉格朗日乘子进行求解。中途飞越的转移轨道优化问题只增加了三维的内点约束，同时增加了三维的拉格朗日乘子χ。由上文的推导过程中可知，在打靶过程中，与乘子χ有关的式并不作为打靶方程的约束，而是在tm时刻对协态变量λr进行更新。考虑到若能在减小χ初值猜测难度的情况下，找到另外一条中间轨道作为初始的中途飞越轨道，则可对中途飞越轨道进行平滑过渡，使航天器最终实现对目标天体的轨道进行飞越。

将航天器需要进行中途飞越的目标天体轨道用经典轨道六要素Ef=[af,ef,if,ωf,Ωf,Mf]来表示，选取初始飞越轨道为Ei=[ai,ei,ii,ωi,Ωi,Mi]，轨道要素中的平近点角M都为初始时刻t0对应的平近点角。具体的处理方法为：

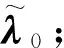
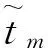
2.2 性能指标的同伦

从式中可以看出，当性能指标为能量最优时，其最优推力大小是连续变化的，此时较容易求解。因此，针对燃料最优的Bang-Bang控制问题，Bertrand等在2002年提出了一种平滑技术，即所谓的同伦方法，通过构造新的性能指标，降低了求解难度[13]。

引入同伦参数q2，构造新的性能指标为

(19)

当q2:0→1过程中，性能指标从能量最优转变为燃料最优。根据最优性一阶必要条件，推力大小u的控制律为

(20)

式中：ε=1-q2，当q2≠1时，u为连续控制力，且q2趋近于1时，即可得到燃料最优的转移轨道。

在得到能量最优问题的转移轨道之后，同伦参数q2按照一定步长进行迭代，并将当前得到的解作为下一步迭代的初值进行计算，并最终得到燃料最优的转移轨道。

3 数值仿真

本节通过两个算例进行数值仿真，验证本文所提出的同伦方法的有效性。

算例1.考虑航天器从地球出发，与火星进行交会，并对小行星2005UK5中途飞越的轨道转移问题。航天器从地球出发时与地球具有相同的日心位置和速度，到达火星时与火星具有相同的日心位置和速度。小行星2005UK5的数据来源于小天体动力学网http://newton.dm.unipi.it/neodys/。算例相关参数如表1所示。

表1 地球到火星交会并中途飞越小行星的算例的参数

先通过打靶求解无中途飞越时的从地球到火星的能量最优转移轨道，根据航天器在转移过程中与小行星的相对距离进行初始飞越点的选取。选取转移轨道上与小行星距离最近的时刻作为初始飞越时刻，转移轨道上的该点作为初始飞越点，然后分两步进行同伦迭代求解：1.保持性能指标为能量最优，对中途飞越点进行同伦，即q2=0，q1:0→1；2.得到对小行星进行飞越的能量最优转移轨道后，再对性能指标进行同伦，即q1=1，q2:0→1，从而得到航天器对小行星2005UK5进行中途飞越的燃料最优转移轨道。

最终得到的转移轨道如图1所示，飞越时刻为294.9028天，航天器最终剩余质量为1649.41kg。图1中的黑色虚线和红色实线分别表示同伦初始时刻的转移轨道和同伦结束时刻的燃料最优转移轨道，同伦结束时刻对小行星2005UK5实现了中途飞越，飞越位置已在图中标出。图2为优化变量在对中途飞越位置同伦过程中随同伦参数q1的变化曲线，图3为优化变量在对性能指标的同伦过程中随同伦参数q2的变化曲线，从图中可以看出，同伦参数连续缓慢变化，同伦过程顺利进行。图4为航天器在转移过程中开关函数和推力随时间的变化曲线，对于q1=q2=0和q1=1,q2=0的两条转移轨道，其性能指标同为能量最优，两条轨道形状较为接近，开关函数和推力大小变化曲线无明显差异；对于q1=q2=1的燃料最优转移轨道，其推力大小变化为Bang-Bang控制，发动机共开机4次。

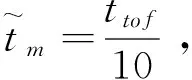
描述量数值初始时刻(UTC)2021-11-160:0:0.0飞行时间ttof/d2201.0天初始位置/AU[0.5876420, 0.7954627, -3.845203×10-5]初始速度[-5.155764,3.707833, -3.191945×10-4]末端位置[-5.204974,1.495369,0.1102444]末端速度[-0.7936872,-2.523063,2.823220×10-2]发动机比冲Isp/s6000发动机最大推力Tmax/N2.26航天器初始质量m0/kg20000.0火星轨道根数[a,e,i,Ω,ω,f]J2000日心黄道坐标系中,参考历元[1.52363312AU,0.09327933,1.84785414°,49.48935357°,286.6709081°,328.887552°]2024-3-200:0:0.0(坐标时)

值得注意的是，在同伦过程中，可设置两个同伦参数相等，即q1=q2，此时则可通过一次同伦过程得到所需的解。在此算例中，令q=q1=q2，同时对中途飞越位置和性能指标进行同伦，通过一次同伦得到中途飞越火星并与木星交会的燃料最优转移轨道。

最终得到的航天器燃料最优转移轨道如图5所示，航天器对火星进行中途飞越的时刻为732.8713天，最终剩余质量为14657.05kg，其中黑色虚线为同伦初始时刻的转移轨道，该轨道为能量最优转移轨道，对其进行求解时不考虑中途飞越内点约束，然后在该轨道上进行选取合适的初始中途飞越位置；红色实线表示同伦结束时的转移轨道，该轨道为对火星实现中途飞越的燃料最优转移轨道。图6为航天器进行中途飞越位置随同伦参数的变化曲线，从图中可以看出，当同伦初始时刻时，航天器并未经过火星，而是对虚拟的目标进行飞越；随着同伦过程的进行，最终实现对火星的飞越。图7为优化变量随同伦参数的变化曲线，从图中可以看出，各优化变量变化平缓，不存在突变或跳跃的情况。图8为当同伦参数q分别取值为0,0.4,0.7,0.9和1.0时的开关函数和推力大小随时间的变化曲线，从图中可以看出，对于燃料最优转移轨道，其最优推力为Bang-Bang控制，在转移过程中发动机开机4次。

4 结 论

本文针对航天器需要对目标天体进行交会，并对其他天体进行中途飞越的连续小推力燃料最优转移轨道进行研究。本文建立了含中途飞越约束的动力学模型，推导得到了最优性条件，提出的同伦方法包含对中途飞越轨道的同伦和对性能指标的同伦。通过数值仿真表明，利用该同伦方法能有效地克服由中途飞越约束所引起的困难，并得到满足任务需求，发动机多次开关机的燃料最优转移轨道。后续工作中，可对包含引力辅助等更复杂的内点约束的小推力转移轨道进行研究。

[1]D'AmarioL,ByrnesD,StanfordR.Anewmethodforoptimizingmultiple-flybytrajectories[J].JournalofGuidance,Control,andDynamics, 1981, 4(5): 591-596.

[2]GrebowD,BhaskaranS,ChesleyS.Search&selectionforfutureflybytargetsfortheDI/EPOXIspacecraft[C].AIAA/AASAstrodynamicsSpecialistConference,Minnesota,USA.August13-16, 2012.

[3]JesickM.Marsdouble-flybyfreereturns[J].JournalofSpacecraftandRockets, 2015, 52(5): 1348-1360.

[4] 乔栋, 黄江川, 崔平远, 等. 嫦娥二号卫星飞越Toutatis小行星转移轨道设计[J]. 中国科学: 技术科学, 2013, 43(5): 487-492. [QiaoDong,HuangJiang-chuan,CuiPing-yuan,etal.TrajectorydesignofCE-2flybyToutatisasteroidmission[J].ScientiaSinicaTechnologica, 2013, 43(5): 487-492.]

[5] 刘磊, 吴伟仁, 唐歌实, 等. “嫦娥二号” 后续小行星飞越探测任务设计[J]. 国防科技大学学报, 2014, 36(2): 13-17. [LiuLei,WuWei-ren,TangGe-shi,etal．Designofanasteroidflying-bymissionforCHANG’E-2 [J].JournalofNationalUniversityofDefenseTechnology, 2014, 36(2): 13-17.]

[6] 曹喜滨, 张相宇, 王峰. 采用Gauss伪谱法的小推力日-火Halo轨道转移优化设计[J]. 宇航学报, 2013, 34(8):1047-1054. [CaoXi-bin,ZhangXiang-yu,WangFeng.Optimizationoflow-thrusttransfertrajectoryfortheSun-Marshaloorbitbasedongausspseudospectralmethod[J].JournalofAstronautics, 2013, 34(8):1047-1054. ]

[7] 李俊峰, 蒋方华. 连续小推力航天器的深空探测轨道优化方法综述[J].力学与实践，2011,33(3):1-6. [LiJun-feng,JiangFang-hua.Surveyoflow-thrusttrajectoryoptimizationmethodsfordeepspaceexploration[J].MechanicsinEngineering, 2011, 33(3):1-6.]

[8] 尚海滨, 崔平远, 徐瑞,等. 结合行星借力飞行技术的小推力转移轨道初始设计[J]. 宇航学报, 2011, 32(1):29-38. [ShangHai-bin,CuiPing-yuan,XuRui,etal.Preliminarydesignoflow-thrusttransfertrajectorywithplanetaryswing-bys[J].JournalofAstronautics, 2011, 32(1):29-38.]

[9] 陈杨, 宝音贺西, 李俊峰. 我国小行星探测目标分析与电推进轨道设计[J]. 中国科学 物理学 力学 天文学, 2011, 41(9): 1104-1111. [ChenYang,Bao-yinHe-xi,LiJun-feng.Targetanalysisandlow-thrusttrajectorydesignofChineseasteroidexplorationmission[J].ScienceChinaPhysics,Mechanics&Astronomy, 2011, 41(9): 1104-1111.]

[10] 郭铁丁. 深空探测小推力轨迹优化的间接法与伪谱法研究[D].北京: 清华大学, 2012. [GuoTie-ding.Studyofindirectandpseudospecrtralmethodsforlowthrusttrajectoryoptimizationindeepspaceexploration[D].Beijing:TsinghuaUniversity, 2012.]

[11]JiangF,BaoyinH,LiJ.Practicaltechniquesforlow-thrusttrajectoryoptimizationwithhomotopicapproach[J].JournalofGuidance,Control,andDynamics, 2012, 35(1): 245-258.

[12] 李俊峰, 宝音贺西, 蒋方华, 等. 深空探测动力学与控制[M]. 北京: 清华大学出版社, 2014.[LiJun-feng,Bao-yinHe-xi,JiangFang-hua,etal.Dynamicsandcontrolofinterplanetaryflight[M].Beijing:TsinghuaUniversityPress, 2014.]

[13]BertrandR,EpenoyR.Newsmoothingtechniquesforsolvingbang-bangoptimalcontrolproblemsnumericalresultsandstatisticalinterpretation[J].OptimalControlApplicationsandMethods, 2002, 23(4): 171-197.

通信地址：陕西省西安市碑林区友谊西路127号西北工业大学251信箱(710072)

电话：15191433469

E-mail：xpan2012@gmail.com

(编辑：张宇平)

Homotopy Method for Fuel-Optimal Trajectory Design in Flyby Mission

PAN Xun1,2, PAN Bin-feng1,2, TANG Shuo1

(1. School of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China; 2. National Key Laboratory of Aerospace Flight Dynamics, Xi’an 710072, China)

A new homotopy method is proposed to solve the fuel-optimal transfer trajectory with flyby of other celestial bodies in the deep space exploration, overcoming the difficulty due to the interior point constraints and discontinuous structure of the Bang-Bang control. The homotopic parameter is embedded in both the performance index and interior point constraint equations. By starting from a related and easier energy-optimal problem without inner constraints, and solving a series of iterative subproblems with homotopic parameter increased, the solution of the original problem is obtained when the parameter reaches one. With the approach, the difficulty of the optimization variables increased caused by the flyby inner constraints can be resolved, and the low-thrust fuel-optimal transfers can be completed effectively. At last, two examples about the Jupiter rendezvous with the Mars flyby and the Mars rendezvous with an asteroid flyby are given to substantiate the effectiveness and optimality of the homotopy method.

Flyby; Optimal control; Fuel optimal; Low thrust; Homotopy method; Deep space exploration

2016-07-20;

2016-12-19

V448.2

A

1000-1328(2017)04-0393-08

10.3873/j.issn.1000-1328.2017.04.009

潘 迅(1990-)，男，博士生，主要研究方向为飞行动力学与控制，深空探测轨道优化设计。