高职班数学运算核心素养的培养

蔡敬发

（厦门市五显中学，福建 厦门 361100）

高职班数学运算核心素养的培养

蔡敬发

（厦门市五显中学，福建 厦门 361100）

高职生整体的数学基础比较薄弱，运算核心素养普遍较低，在日常的课堂教学中，教师可通过“精心设计，引领课堂”“师生探究，共同发现”“变式思考，优化重组”“一题多用，反思巧解”“渗透思想，提高效率”等具体措施提高学生的运算核心素养。

高职生；数学运算核心素养；思想；探究；渗透

随着基础教育课程改革的深入推进，课堂教学的关注已从知识传授和技能训练转至核心素养培养。《普通高中数学课程标准》已提出中国学生在数学学习中应培养好数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析六大核心素养，其中数学运算素养是基础的、不可或缺的一项核心素养。

厦门市五显中学是一所地处农村的省二级达标校，学生的数学运算核心素养较低。尤其是高职生，数学基础更为薄弱，运算核心素养的培养任重而道远。基于此，笔者通过“一精三步多渗透”的探究、实施及反思，有针对性地对高职生进行了数学运算核心素养的培养，其设计脉络如下：

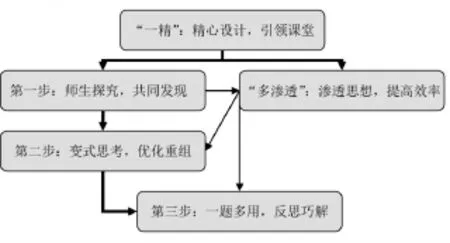
在日常教学的过程中，各环节都有值得认真探讨的问题，例谈如下：

一、精心设计，引领课堂

1.设计魔术，激发兴趣

针对部分学生常常在计算时无法想到对应图形的实际情况，笔者设计了一段“小魔术”教学。笔者在讲台上排了9张正面向上的扑克，分别是1—9，组成一个矩形。教师正面对着黑板，背靠着扑克，让学生上讲台用手指头指向一次扑克牌，教师转身，九张扑克重新洗牌，然后洗出了学生所指的那张扑克。重复几次，让学生不可置信。其实，笔者在学生中设了一个“托”，借助数学课本和九张扑克的矩形相似，在洗牌的过程通过“托”的提示，实现“托”的形和扑克的数有效融合，从而创造了“神奇的洗牌”。数形结合的思想也能结合魔术教学，让学生意想不到，兴趣也就自然被激发了。

2.设计探究，注重形成

对高职生而言，往往探究过程比问题的结论更重要，忽视形成过程的结论是记不住、用不活的。因而，笔者的复习教学常常以探究的形式围绕展开。

3.设计类比，加强体验

数学运算核心素养是指在明晰运算对象的基础上，依据运算法则解决数学问题的思维过程。［1］关于对法则的选择，笔者以为，类比体验是一种高效的方式。比较见真知，在类比中培养数学运算核心素养。

二、师生探究，共同发现

数学素养的培养并不仅是教师传授了什么，更重要的是学生发现了什么，感悟了什么？笔者以为，高职班的数学运算探究，有利于细化问题的台阶，循循善诱，在师生互动中共同发现问题的本质，从而提高学生的数学运算核心素养。

例：基本不等式复习的课堂实录。

师：大家算一下 f(x)=sin x+2(sin x≠0)的最sin x小值？

师：根据什么算的？

生：基本不等式（均值不等式）。

经教师提醒，学生议论纷纷，好像可以为负值呢，好像没最小？

师：大家忽略了使用均值不等式的首要条件是“一正”，怎么办，是不是不能用均值不等式？

师：哦，挺不错的，先转化为“一正”，很棒！这么说，最小值可正可负，那如果先限定sin x＞0，是不是最小值就是？如果是，大家解方程：，怎么样？

在师生的共同探究中，学生发现均值不等式不该仅记“一正、二定、三等”，更要探究它的形成，感悟到“一同、二定、三等、四换元”的运算要领。接下来，笔者抛出了以下运算题组：

学生顺势就准确计算出来了。紧接着，笔者又抛出以下探究题组：

一环紧扣一环的探究，学生不断有新的发现，数学运算核心素养得到有效的提高。

三、变式思考，优化重组

运算素养包括分析运算条件，探究运算方向，选择运算公式，确定运算程序等一系列过程中的思维素养，也包括在实施运算过程中遇到障碍而调整运算的素养以及实施运算和计算的技能。［2］笔者以为，变式思考，有利于学生对数学运算重新建构，优化重组，从而提高运算的灵敏性、准确性。

在数列的复习中，笔者与学生做了如下师生互动：

师：an+1=can+d中，当c=1,d≠0,那是什么情况，如an+1=an+2？

生：是等差数列呀。

师：当c=1，d=f(n)，那是什么情况，如an+1=an+n？

生：哦，构造an+1-an，是累加型的。

师：an+1=can+d中，当c≠1,d=0,那是什么情况，如 an+1=3an？

生：是等比数列。

师又问：an+1=can+d中，当c≠1，d≠0，那是什么情况，如an+1=2an+1？

生：不是等差，也不是等比，是什么？

师：怎么转化成等差或等比来处理？这是加k型。

接着，师生共同把常见的递推模型进行了梳理：

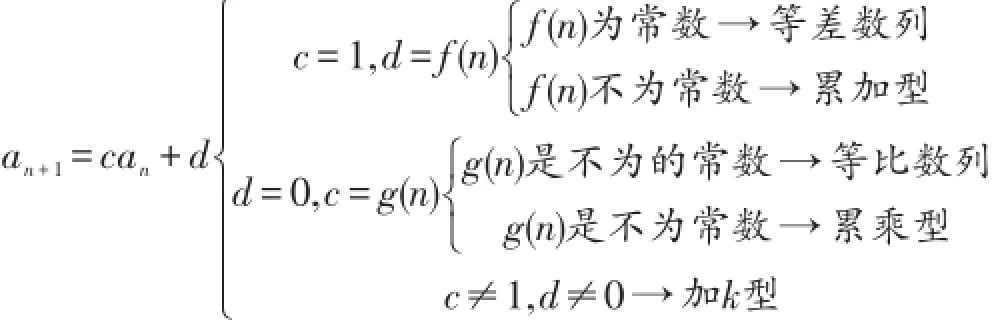
上面的师生互动以递推公式为主线，通过c、d的变化，引出了数列这章的两个特殊数列及三个重要方法：累加、累乘、加k，让学生对数列的认识进行了优化重组，提高了数列题型的运算效率。在变式思考中，笔者还常变式题设、变式结论、变式想象等，都是为了对学生的认知进行重组，对运算核心素养进行培养与提高。

四、一题多用，反思巧解

数学运算要有“四性”：准确性、合理性、熟练性及简捷性。笔者以为，农村校高职生课堂的容纳量有限，对例题必须精挑细选。因而，只有达成一题多用，才能既体现课堂复习重点，又能体现解题技巧，既让学生动手练习，又是师生探究的载体，让学生在巩固、类比中培养数学运算核心素养，从而达到“四性”的要求。

笔者在复习《等比数列》的课堂中让学生先做以下题目：

练习：已知等比数列{}an的各项均为正数，且a5a6+a4a7=18，则log3a1+log3a2+...+log3a10=( )

A．12 B.10 C.8 D.2+log35

师生探究1：从解决数列问题的基本思想看，可把问题回归给首项与公比进行处理，对这题来说，运算相对繁琐。

师生探究2：从等比数列运算性质看，到5+6=4+7，故有a5a6=9，而log3a1+lg3a2+...+log3a10=log3(a1a2a3a4a5a6a7a8a9a10)，再观察到1+10=2+9=3+8=4+7=5+6，从而可都化为a5a6来解决。项数先行，巧用性质，激活了学生思维，提高了运算的准确率。

师生探究3：既然这是一道选择题，就可能寻找更简 洁 的 方 法 。 有 a5a6+a4a7=18 ，如 果 取a3=a4=a5=a6=3可以吗？一题多解，反复推敲，学生的运算热情到了一个高点。

师生探究4：已知等差数列{}an，且a4+a5+a6+a7=4，则2q1·2a2·2a3·...·2a10 =____________（填空题）。

可以想象，师生探究1、2、3的方法都会有一部分同学采纳，但是采纳探究3方法的同学会更多了。在师生探究4中，教师类比了等差数列与等比数列的性质，同时又强化了探究1、探究2及探究3的方法，加强了学生的运算体验。一道题引出了一堂课的复习主题，反复使用，多而不杂，在平淡中掀起了运算的涟漪，提高了学生的数学运算核心素养。

五、渗透思想，提高效率

部分教师甚至认为，对农村高职生而言，数学思想与方法过于“高大上”。其实，数学的准确计算是离不开数学思想的，渗透思想对高职生的运算核心素养的提高是非常重要的。

在“小魔术”教学中，笔者通过数形结合思想的渗透，激发了学生学习的兴趣，提高了运算效率。

在数列的复习教学中，笔者渗透了函数与方程的思想、类比的思想及转化与化归的思想，加强体验，提高了数学运算核心素养。

笔者认为，在日常教学中，需要教师不断渗透数学思想，腾出时间对四大数学思想进行再梳理，这对提高学生的数学运算核心素养有许多益处。

在近几年的高职班的数学教学中，笔者都十分重视学生数学运算核心素养的培养，在近几届高职高考中，学生的数学学科均取得了优异的成绩，数学运算核心素养的培养效果显著。当然，农村校高职生数学运算核心素养的培养工作任重道远，需要笔者继续在实践中反思，在反思中提升！

［1］陈春涛.从一道错题看章节起始课对数学运算核心素养的影响［J］.中学数学，2016（20）.

［2］万东.高中学生数学运算能力的培养研究［J］.中学数学研究，2016（11）.

［3］卢小妹.关于高中数学核心素养的认识［J］.福建中学数学，2016（6）.

［4］陈玉娟.例谈高中数学核心素养的培养——从课堂教学中数学运算的维度［J］.数学通报，2016（8）.

（责任编辑：王钦敏）

福建省教育科学“十二五”规划2015年度一般课题（项目编号：FJJK15-447）。