三视图的一个重要应用
——多面体的外接(内切)球半径的求法举要
湖北省巴东一中(444300) 张世林●
湖北省恩施高中(445000) 谭 斌●
三视图的一个重要应用
——多面体的外接(内切)球半径的求法举要
湖北省巴东一中(444300)
张世林●
湖北省恩施高中(445000)
谭 斌●
求三视图还原而成的几何体的外接(内切)球的表面积或体积的问题在2016届各地的高考模拟题中大量出现,这是高考的重点,也是学生学习的难点.困难表现在两个方面:一是根据三视图如何准确还原几何体;二是依据画出的几何体的特征如何采用适当的方法求外接(内切)球的半径.现就此类问题的常见求法举例分析如下.
一、找“墙角”
例1 已知某几何体的三视图如图所示,则该几何体的外接球的表面积为( ).
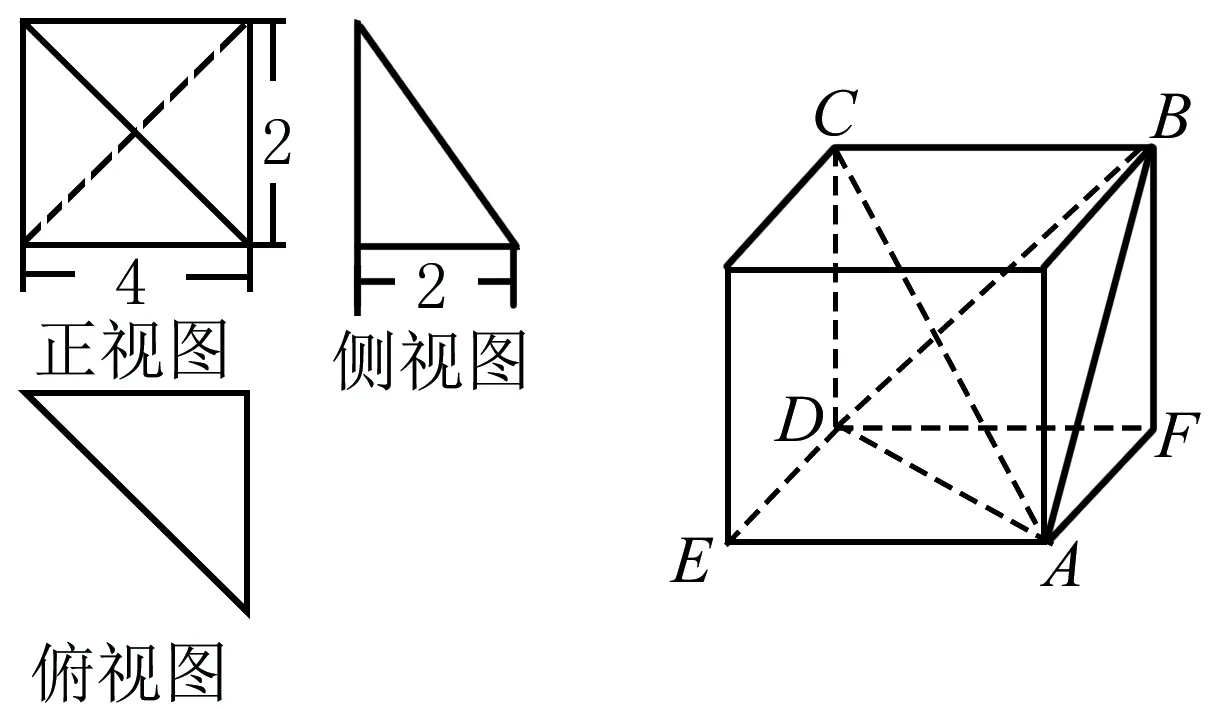

解析 如图,还原的多面体就是三棱锥A-BCD,其外接球也是此三棱锥所在的长方体的外接球.注意:DC,

二、寻外心
①当几何体中出现两个垂直关系,利用直角三角形斜边的中线等于斜边一半,球心为直角三角形斜边中点(即直角三角形的外心).
② 因为球心与截面圆圆心的连线垂直于截面圆,截面圆上的点与圆心、球心构成直角三角形,运用公式R2=r2+d2求半径.



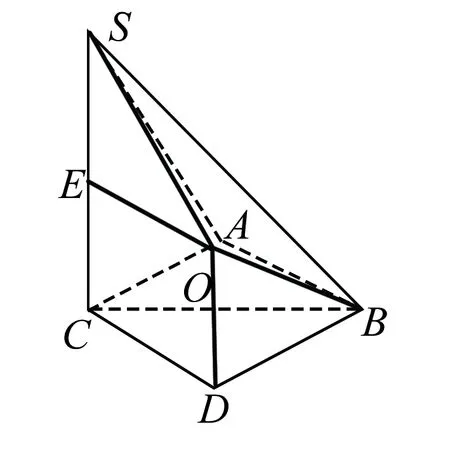
例3 已知三棱锥S-ABC的顶点都在球O的球面上,且SC⊥平面ABC,若SC=AB=AC=1,∠BAC=120°,则球O的表面积为____.

变式 一几何体的三视图如左图,则它的外接球的表面积为( ).
A.12πB.16πC.20πD.24π

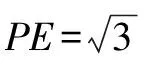
三、作截面
通过寻找外接球的一个轴截面圆,把立体几何问题转化为平面几何问题来研究.
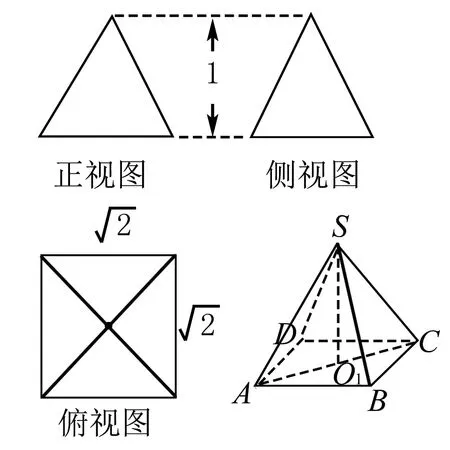
例4 已知一几何体的三视图如右图所示,则此几何体的外接球的体积为____.

四、用结论

例5 如右下图所示为某几何体形状的纸盒的三视图,在此纸盒内放一个小正四面体,若小正四面体在纸盒内可以任意转动,则小正四面体的棱长的最大值为( ).

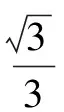
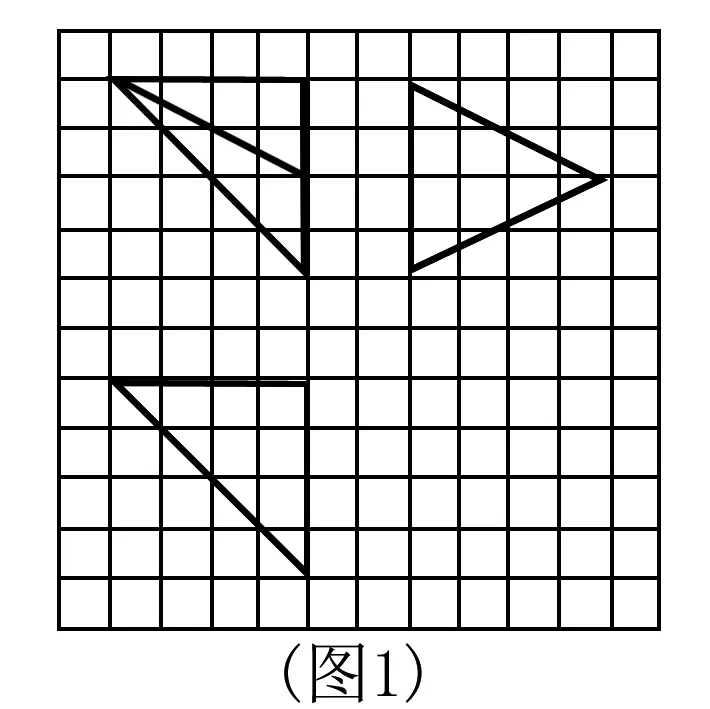
巩固练习1.如图1,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体外接球的表面积为____.
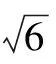
3.如图2是某几何体的三视图,求该几何体的体积.
4. 如图3,网格纸上小正方形的边长为2,粗线画出的是某几何体的三视图则该几何体的体积是____.

5. 如图4,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体外接球的表面积为____.
答案:1. 41π;2.16π;3. 8/3 4.14π5.41π/4
G
B
1008-0333(2017)10-0013-02

