一道常见题型的拓展分析
扬州大学附中东部分校(211400) 朱云峰●
一道常见题型的拓展分析
扬州大学附中东部分校(211400)
朱云峰●
本文主要探讨一道常见题型的深挖拓展,增加学生的拓展面,提高教学效率,更好地减轻学生的学习负担.
机械能守恒;圆周运动;深化;挖掘
中学物理中圆周运动与机械能守恒经常是结合起来考查学生的.笔者对一道圆周运动与机械能守恒相结合的常见题型,深入探究,拓展分析,并与解答,谈谈我的看法,题目如下:
原题 用长为L的细绳系着一个质量为m的小球固定在O点,绷紧细绳,在水平位置静止释放小球,在O点正下方有根钉子O1,使得小球围绕钉子O1做圆周运动,求小球做圆周运动的半径,如图1.

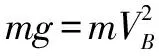
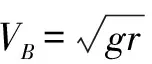
拓展一 : 如果小球低于水平位置,且与水平位置成θ角,绷紧细绳,静止释放,在O点正下方某处有一钉子O2, 使得小球围绕钉子O2做圆周运动,求小球做圆周运动的半径,如图2.
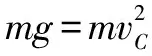

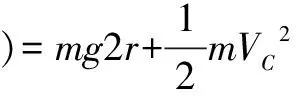
比较释放前小球离零势能面的高度h前和释放后小球围绕钉子O2做圆周运动到达C点时离零势能面的高度h后
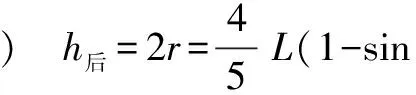
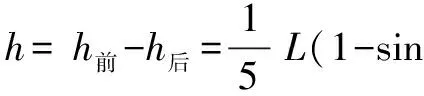
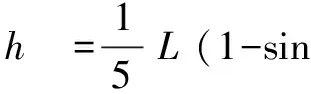
拓展分析二 如果小球高于水平位置,且与水平位置成θ角,绷紧细绳,静止释放,在O点正下方某处有一钉子O3使得小球围绕钉子O3圆周运动,求小球做圆周运动的半径,如图3.
解 小球从A点到A1自由落体运动,由机械能守恒得:
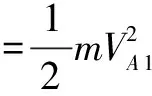
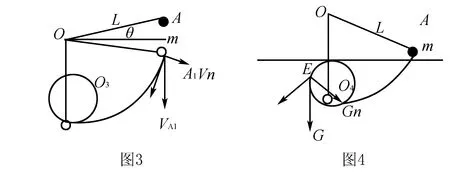
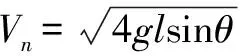
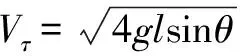
在A1处由于绳子绷紧过程中,拉力做功,小球在A1处的法向速度瞬间为零.
A1点到D点机械能守恒,以小球为研究对象得:
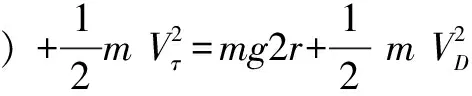
小球在D处恰好做圆周运动,在最高点B处,由重力提供向心力
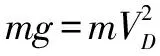
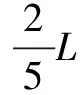
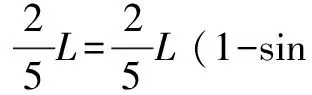
化简:sinθ=2sinθcos2θ
错解 点A、E在等高的水平线上,由于机械能守恒,小球能回到E点,且 VE=0

正确解法:(1)小球在A点的机械能:
EKA=mg2r
小球到达E点的最小机械能为:
EKA>EKE
∴小球不能到达点E
(2)假释小球运动到点D离开圆形轨道,做斜抛运动,连接O4D,与竖直方向夹角为α,α确定,故D点位置确定.
如图4,在D处小球由重力的一个分力Gn= Gcosθ= mgcosθ⑧提供向心力,即Gn= f向=mVD2/r ⑨
根据(A、D两点)机械能守恒:
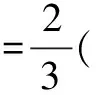
向上面这道普通题型的深化,挖掘,对学生思维的发展,知识的掌握和灵活运用,有重要的影响.在教学工作中,我们也要不断的深化学习.
G
B
1008-0333(2017)10-0072-02

