轴向冲击作用下嵌套式薄壁球壳结构吸能性能研究及优化设计

戎 翔， 邓安仲， 李 飞， 陈 晨

(1.后勤工程学院 化学与材料工程系，重庆 401311;2.后勤工程学院 军事工程管理系，重庆 401311;3.后勤工程学院 信息工程与军事物流管理系，重庆 401311)

轴向冲击作用下嵌套式薄壁球壳结构吸能性能研究及优化设计

戎 翔1， 邓安仲2， 李 飞2， 陈 晨3

(1.后勤工程学院 化学与材料工程系，重庆 401311;2.后勤工程学院 军事工程管理系，重庆 401311;3.后勤工程学院 信息工程与军事物流管理系，重庆 401311)

针对单个小直径薄壁球壳吸能能力有限的问题，提出了一种嵌套式薄壁球壳结构，并通过有限元软件模拟其在轴向冲击下的动态响应过程，分析了外球壳厚度、内球壳高度和内球壳厚度对结构在轴向冲击下力学性能和变形模式的影响；建立了以比吸能、冲击荷载峰值为吸能性能的评价指标，以外球壳厚度、内球壳高度和内球壳为试验变量的响应表面模型；基于响应表面模型，通过非支配遗传算法(NSGA-Ⅱ)对试验变量进行优化，提出了不同工况下结构几何参数选取方案。结果表明，结构几何参数对其吸能特性影响显著，建立的响应表面模型准确可靠，优化方法得到了有限元模拟验证，有利于工程实际应用。

吸能；嵌套式薄壁球壳；响应表面；遗传算法

随着高抗力、大跨度防护门的发展，为减轻门体质量，抵御常规武器爆炸冲击，节约成本，势必要研究新型轻质、吸能性能优异的加固材料，这是防护工程发展的一个重要方向[1]。夹芯材料因其在吸能减振方面的优异性能，受到了国内外学者的广泛关注。夹芯材料一般是由两层高强度薄面板和中间轻质芯层通过焊接或胶接而成，它结合了面板材料抗弯曲、拉伸能力强和芯层材料塑性变形吸能的优势。随着现代工业的发展，薄壁球壳作为芯层材料常见结构形式，在轴向冲击作用下，能够通过自身不可逆的塑性变形显著地耗散冲击动能，且具有轻质、跨度高和承载能力高等优点[2]。

针对薄壁球壳结构的力学性能已进行了许多相关实验及模拟研究工作。Updike[3-4]研究了轴向冲击荷载下刚塑性球壳的压缩变形模式，并提出了一种关于轴向荷载-位移之间关系的分析模型；Gupta等[5-6]研究了轴向准静态压缩时薄壁球壳的弯曲变形模式，以及通过落锤实验分析动态冲击下薄壁球壳的动态响应，主要考虑球壳半径和厚度的变化对其力学性能的影响；Shariati等[7]对三种直径(102 mm、77 mm、53 mm)薄壁球壳结构受刚性平面、长方体、圆柱等不同形式轴向荷载下的力学性能进行了研究，并对平均轴向荷载的变化规律进行了讨论；马春生等[8]通过试验研究了附加质量块的薄壁球壳冲击刚性地面的动态吸能特性，并利用了镜面反射理论得到了径厚比较大时轴向撞击力随压缩位移变化的力学模型。

基于以上分析，可知同种材料薄壁球壳吸能能力主要由球壳厚度和球壳半径决定。而夹芯吸能材料应用于防护门加固中对自重和厚度都具有一定的要求，若自重与厚度太大，加固后可能增加防护门的启闭难度[9]。因此，应用于防护门加固中的夹芯材料芯层只允许小直径薄壁球壳结构形式,而单个小直径薄壁球壳的吸能能力和承载能力相对有限。针对这一问题，本文提出一种嵌套式薄壁球壳结构，并通过一系列有限元数值模拟研究嵌套式薄壁球壳结构在轴向冲击下的动力响应，探讨了结构几何参数对其力学性能的影响，最后基于吸能指标对几何参数进行优化设计，为工程应用提供基础。

1 吸能效率评价指标

为准确量化评估薄壁结构的吸能效率，参考文献[10]定义一组评价指标：吸能值(Energy Absorption，EA)、比吸能(Specific Energy Absorption，SEA)及轴向冲击荷载峰值(Peak Crush Load，PCL)。其中，吸能值(EA)代表轴向冲击作用下薄壁结构吸收的总能量，可表示为

(1)

式中:L表示轴向冲击荷载；d表示薄壁结构在冲击作用下产生的轴向压缩位移。为便于分析比较不同薄壁结构的吸能能力，d统一取结构变形量的75%。

比吸能被定义为单个薄壁结构单元吸收能量值与其质量之间的比值，表示为

(2)

式中，M为单个薄壁构件质量。当比吸能越高，薄壁结构吸能效率也越高。

PCL(Peak Crush Load)表示为薄壁结构在轴向压缩过程中受到的冲击荷载峰值。

2 有限元模拟

2.1 几何构型

本文研究的嵌套式薄壁球壳结构几何示意图如图1所示。某一实际应用中夹芯吸能材料芯层厚度为30 mm，即外球壳外径R=30 mm，厚度d1分别取为0.8 mm、1.0 mm、1.2 mm、1.4 mm、1.6 mm；内球壳高度H分别取为10 mm、15 mm、20 mm、25 mm，厚度d2分别取为0.8 mm、1.0 mm、1.2 mm、1.4 mm、1.6 mm。根据嵌套式薄壁球壳结构的几何参数，可用d1-L-d2简化代表一种构型。例如：1.4-20-1.6表示一种嵌套式薄壁球壳构型，其外球壳厚度为1.4mm，内球壳高度为20mm，厚度为1.6mm。

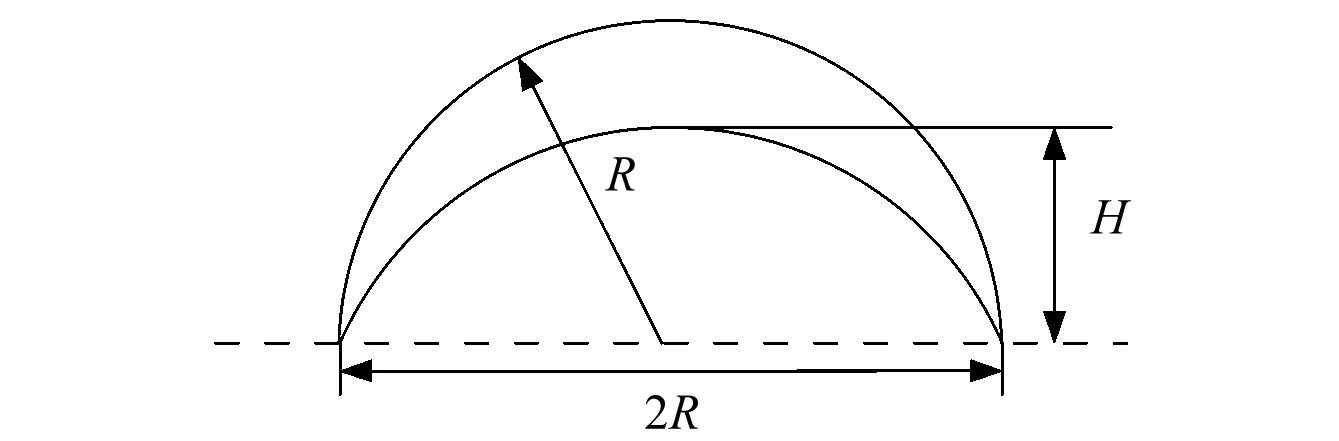
图1 嵌套式薄壁球壳结构几何示意图Fig.1 Geometry description of nested thin-wall spherical shell

2.2 有限元建模

为更好地分析嵌套式薄壁球壳结构在轴向冲击条件下的动力响应过程，本文参考文献[6]中的模型，并采用非线性显式有限元软件LS-DYNA进行分析求解。

如图2所示，加在冲击端的刚体质量为27kg，且约束除轴向位移外其他方向的自由度，给予轴向初速度5m/s。球壳壁采用全积分Belytschko-Tsay壳单元算法进行模拟，沿厚度方向采用5个积分点，单元特征长度取1mm。薄壁球壳底端施加固定的边界条件。分析过程中采用自动单面接触算法(CONTACT-AUTOMATIC-SINGLE-SURFACE)以考虑球壳自身变形可能产生的接触，以及采用面-面侵彻接触算法(CONTACT-ERODING-SURFACE-TO-SURFACE)考虑刚体与球壳之间的接触，同时考虑刚体与球壳之间的摩擦作用，取面与面间的静、动摩擦因数均为0.1。

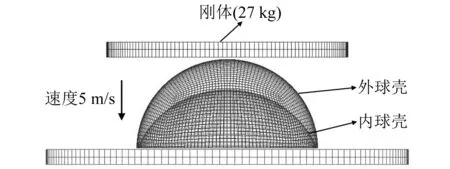
图2 嵌套式薄壁球壳结构有限元模型Fig.2 Finite element model of nested thin-wall spherical shell

球壳采用理想弹塑性铝合金材料，密度ρ=2.74×103kg/m3，杨氏模量为68.9 GPa，泊松比为0.3，材料的真实应力-应变曲线如图3所示。本文采用LS-DYNA中123号材料模型(MAT-MODIFIED-PIECEWISE-LINEAR-PLASTICITY)进行分析。由于铝合金材料对应变率不敏感，所以有限元建模时不考虑应变率效应对材料参数的影响。

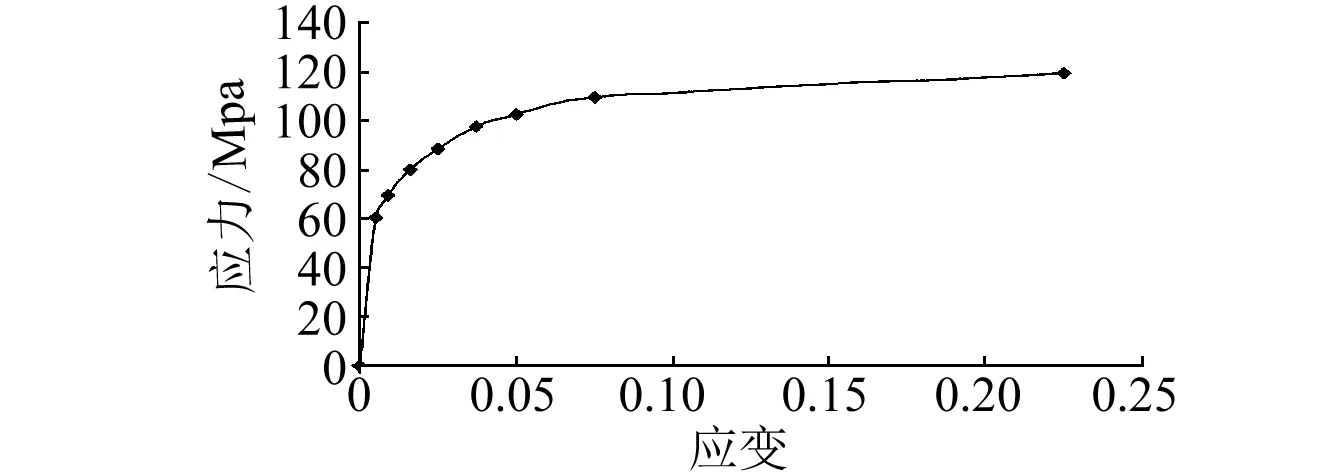
图3 真实应力-应变曲线Fig.3 True stress-strain curve

2.3 有限元模型

为验证所建立的薄壁球壳有限元模型的准确性，根据文献[6]中的试验模型，对一内径为45 mm、高度为45.3 mm及壁厚1.18 mm的薄壁球壳进行轴向冲击模拟。将有限元模拟结果与文献中的试验结果对比，如图4所示。如果仿真和试验误差在20%以内，则可认为仿真模型是正确的。从图4中可以看出，有限元模拟得到的荷载-位移曲线与试验所得相比，变化规律较一致。且通过对比有限元模拟与试验条件下薄壁球壳的吸能效率指标，如表1所示，可以明显地看出，模拟结果与试验结果吻合较好，验证了本文所建立的有限元模型的正确性和有效性。

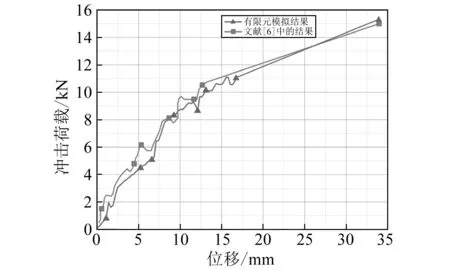
图4 有限元模拟结果与试验结果对比Fig.4 Finite element simulation results compared with the test results

吸能值(EA)/kJ峰值荷载(PCL)/kN有限元模拟结果0.35215.016试验结果0.33915.325

2.4 动态响应影响因素分析

根据2.1中嵌套式薄壁球壳结构几何参数的设置，采用全因子试验方法，总共进行100组试验，得到不同几何参数的嵌套式薄壁球壳结构在轴向冲击条件下的动态响应过程并分析影响因素。

2.4.1 外球壳厚度的影响

外球壳厚度对于嵌套式薄壁球壳结构变形模式和吸能性能具有显著的影响。因此，将内球壳高度设定为15 mm、厚度设定为1.2 mm，比较不同外球壳厚度对结构力学性能的影响，如图5所示。从图中可以看出，随着外球壳厚度增加，结构抗轴向冲击荷载能力显著增强。且当外球壳厚度相对于内球壳厚度较小时，结构的变形模式也发生变化。对于构型1.6-15-1.2，当外球壳与内球壳同时压缩变形时，外球壳壁发生屈曲变形但并未形成皱褶；而对于构型0.8-15-1.2，当压缩到一定程度后，外球壳发生屈曲变形并向内形成皱褶，此时结构抗冲击荷载到达谷值。这一现象产生的原因是当外球壳厚度降低时，薄壁屈服膜力减小，压缩外球壳形成皱褶所需荷载也降低。

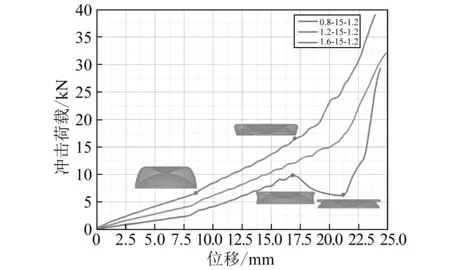
图5 不同外球壳厚度对轴向冲击荷载-位移影响Fig.5 Effect of the thickness of outer spherical shell on the axial crushing load-displacement

2.4.2 内球壳高度的影响

对于嵌套式薄壁球壳结构，内球壳高度是影响吸能效率的关键因素。在保证外球壳厚度和内球壳厚度一定的前提下(同时取1.4 mm)，通过调整内球壳高度，分析其对结构在轴向冲击作用下动态响应的影响。图6为不同内球壳高度下嵌套式薄壁球壳结构的轴向冲击荷载-位移曲线，可以发现当内球壳高度较大时，轴向冲击荷载-位移呈近似分段线性规律。第一个线性段为外球壳产生塑性变形到外球壳凹陷部分边缘与内球壳顶端相接触；接着外球壳与内球壳同时成轴对称向内凹陷，直到内球壳凹陷部分边缘与底面相接触，这一段为第二个线性段；最后外球壳与内球壳不但顶端同时成轴对称向内凹陷，而且凹陷部分底部与底面接触后凸起，形成第三个线性段。当内球壳高度较低时，嵌套式薄壁球壳结构在轴向冲击作用下的轴向冲击荷载-位移曲线也发生了变化。与内球壳高度较高时一样，内球壳高度较低时轴向冲击荷载-位移曲线同样经历前两个线性段，之后曲线发生了“突跳”后进入屈服平台段，此时轴向压缩位移增大而轴向冲击荷载变化很小。

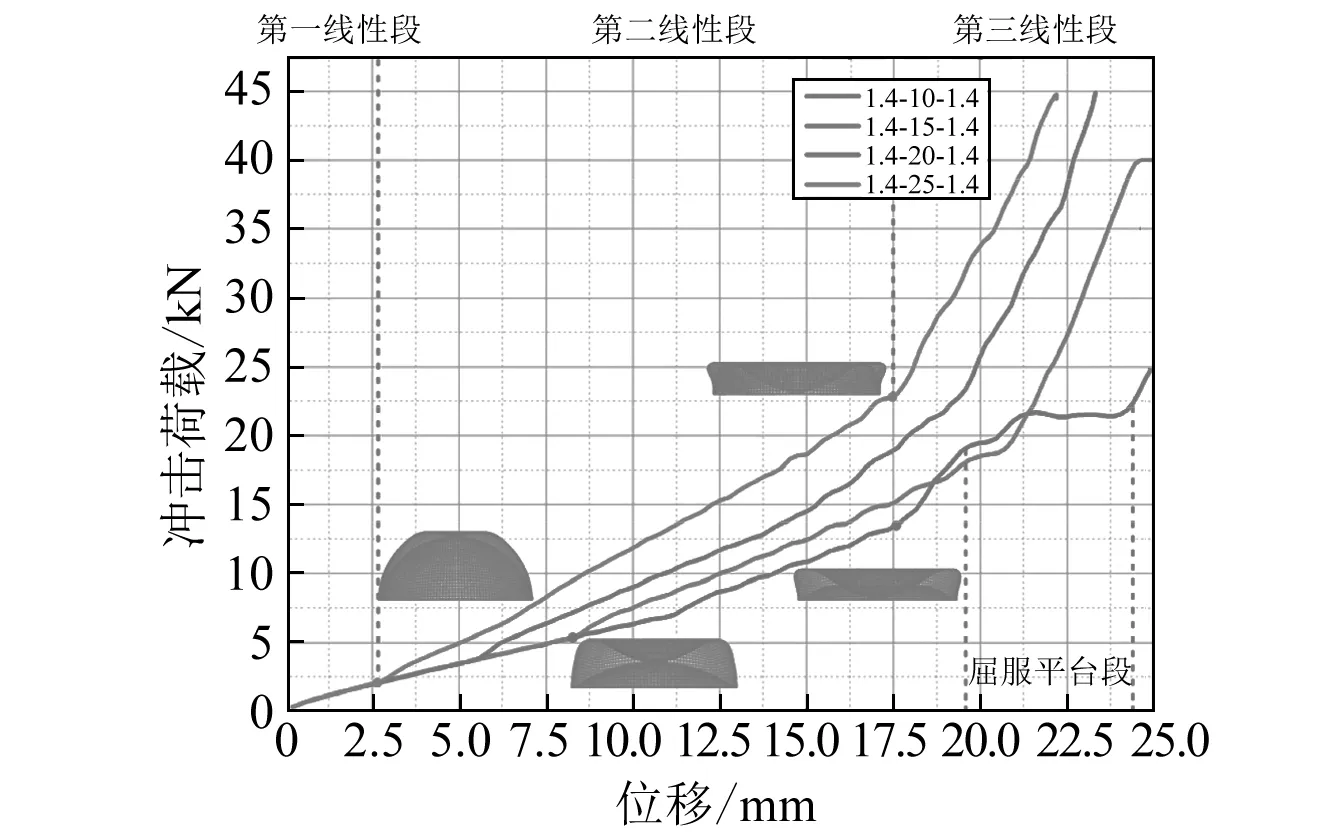
图6 不同内球壳高度对轴向冲击荷载-位移影响Fig.6 Effect of the height of inner spherical shell on the axial crushing load-displacement

2.4.3 内球壳厚度的影响

为研究内球壳厚度对嵌套式薄壁球壳结构承受轴向冲击性能的影响，取外球壳厚度均为1.2 mm、内球壳高度均为25 mm，对不同内球壳高度的嵌套式薄壁球壳结构进行轴向冲击有限元模拟，得到结果如图7所示。由图可见，内球壳厚度的不同并没有改变结构变形模式，结构轴向冲击荷载-位移仍然呈近似分段线性规律。当进入第二个线性段后，外球壳向内凹陷的部分与内球壳顶端相接触，此时内球壳的作用主要是延阻外球壳向内凹陷。而内球壳厚度的增大，提高了压缩内球壳所需荷载，从而使外球壳向内凹陷的作用力变强，造成轴向冲击荷载-位移曲线中第二、第三个线性段斜率增大。

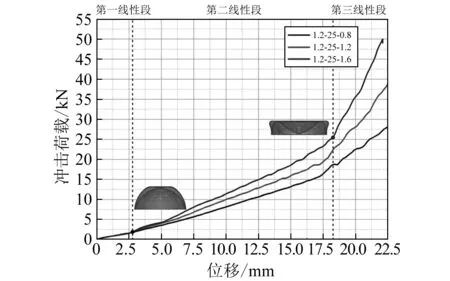
图7 不同内球壳厚度对轴向冲击荷载-位移影响Fig.7 Effect of the thickness of inner spherical shell on the axial crushing load-displacement

3 多目标优化方法

3.1 问题描述

作为轻质夹芯吸能材料芯层结构形式，嵌套式薄壁球壳结构需要在单位质量内吸收足够多的能量。因此，将比吸能(SEA)作为优化模型中的一个目标函数。此外，结构在轴向压缩过程中受到的冲击荷载峰值(PCL)需要被限定在一定范围之内。因为当PCL越大时，夹芯材料作用到被保护结构上的荷载也越大，可能破坏结构的安全性。所以，将降低PCL作为另一个优化目标。综合不同的优化目标，优化问题可以表示为：

(3)

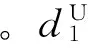
3.2 响应表面法

由于轴向冲击条件下嵌套式薄壁球壳结构的吸能分析是一个高度非线性问题，因此难以给定试验变量与目标间功能函数的明确表达式。为解决这个问题，本文在优化过程中引进响应表面法(Response Surface Methodology，RSM)。RSM是一种高效的试验设计和统计分析的方法[11]，主要用于寻求一个或多个试验变量与若干个目标量之间的关系。响应面试验以外球壳厚度d1、内球壳高度H、内球壳厚度d2为输入，以比吸能(SEA)和负冲击荷载峰值(-PCL)为输出(响应值)，总共进行100组试验，使用Design Expert 8.0软件分析试验数据，计算回归方程。响应曲面优化试验因素及水平设计见表2。

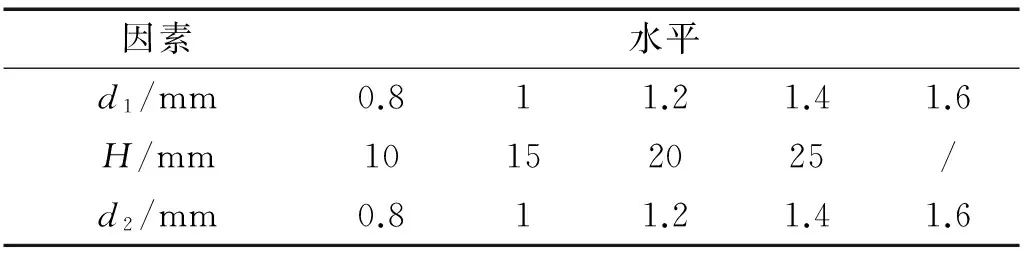
表2 试验因素及水平

3.3 多目标遗传算法

针对多目标优化问题很难存在每个目标函数均为最优的全局最优解的情况，本文拟使用多目标遗传算法(Multi-Objective Genetic Algorithm，MOGA)，该算法主要是在满足约束条件的参数空间内搜索Pareto最优解集。MOGA是基于群体进化的全局搜索优化算法，具有全局寻优能力，且通过MATLAB编程易于实现、运行速度快，将其与RSM结合，可以快速地找出多目标函数的Pareto解集。本文利用非支配遗传算法(NSGA-Ⅱ)来寻找嵌套式薄壁球壳结构设计参数中的Pareto最优解集。作为NSGA的改进版本，NSGA-Ⅱ通过采用更加先进、合理的无支配性排序算法，使整个搜索寻优过程更加有效。本文中使用的NSGA-Ⅱ相关参数见表3。

表3 NSGA-Ⅱ相关参数

4 优化结果分析

4.1 响应值与试验变量的关系模型

采用Design Expert 8.0对试验数据进行分析，得到响应值与试验变量之间关系的多种拟合模型的准确性比较，见表4。

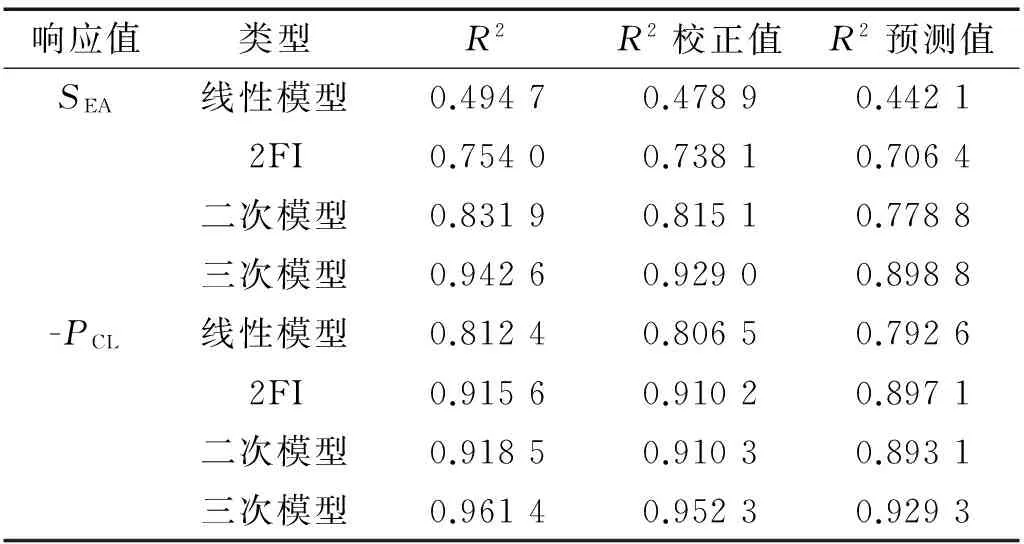
表4 多种拟合模型的准确性比较

从表4中比较结果来看，三次多项式模型为最优；且三次多项式模型是显著的(p<0.000 1)，这说明模型充分代表了真实函数。响应值SEA、-PCL对试验变量(d1、H、d2)的三次多项回归方程如下：

(4)

(5)

图8、图9为各响应值的学生化残差与概率分布图。分析发现，图中学生化残差各点大部分落在直线附近，这表明响应表面法拟合效果均很好。

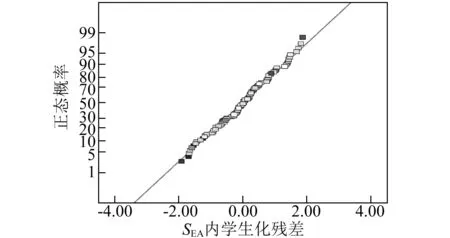
图8 SEA学生化残差分布Fig.8 Normal probability plot of SEA

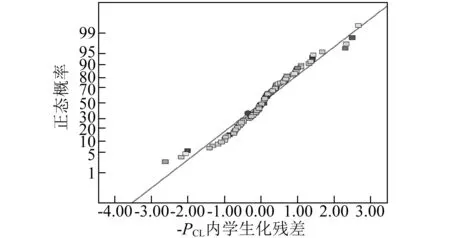
图9 -PCL学生化残差分布Fig.9 Normal probability plot of -PCL

4.2 优化试验变量

在获得SEA、-PCL响应表面模型的基础上，通过NSGA-Ⅱ对试验变量进行优化，得到多目标优化的Pareto最优解集，其Pareto前端分布如图10所示。

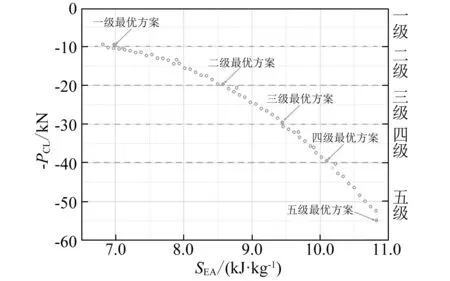
图10 Pareto前端分布Fig.10 Distribution of Pareto front

作为夹芯吸能材料芯层结构形式，嵌套式薄壁球壳结构承受的轴向冲击荷载越大，其作用到被保护结构上的荷载也越大，可能造成夹芯材料失效。因此，根据被保护结构所能承受的轴向荷载级别不同，选取不同的优化方案。本文定义被保护结构能够承受轴向荷载在0～10 kN内为一级，10～20 kN内为二级，20～30 kN内为三级，30～40 kN内为四级，40～60 kN为五级，并根据此优化试验变量。为进一步验证5.1中响应表面模型以及优化方案的准确性，对选取的优化试验变量进行有限元模拟，并将有限元模拟结果与NSGA-Ⅱ优化结果比较，结果见表5。由表5可知，有限元模拟结果与NSGA-Ⅱ结果比较一致，验证NSGA-Ⅱ优化的有效性。

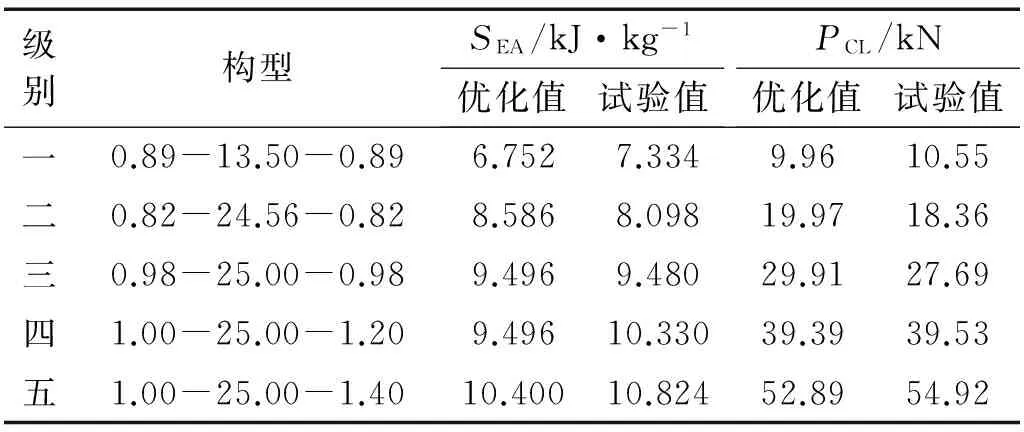
表5 有限元模拟结果与NSGA-Ⅱ优化结果比较

5 结 论

(1)提出一种用于轴向冲击吸能的嵌套式薄壁球壳结构，并采用有限元数值模拟研究了几何参数对结构动态响应的影响。结果表明，提高外球壳厚度、内球壳高度、内球壳厚度都能增强结构抗轴向冲击能力。且当外球壳厚度与内球壳厚度比值变化时，结构的变形模式同时发生变化。

(2)通过Design-Expert 8.0对轴向冲击条件下嵌套式薄壁球壳结构的吸能效率进行分析，建立响应值(SEA，-PCL)与试验变量的关系模型，结果见式(4)和(5)。

(3)通过非支配遗传算法(NSGA-Ⅱ)对嵌套式薄壁球壳结构几何参数进行多目标优化，获得有实用价值的Pareto最优解集，有限元模拟结果验证了响应表面模型以及优化算法的准确性。

[1] 郭东. 爆炸荷载作用下防护门的动态响应行为与反弹机理研究[D]. 北京:清华大学, 2012.

[2] 张威. 薄壁球壳结构的动力学行为与优化设计[D]. 太原:太原理工大学, 2015.

[3] UPDIKE D P. On the large deformation of a rigid-plastic spherical shell compressed by a rigid plate[J]. Journal of Manufacturing Science & Engineering, 1972, 94(3):949-955.

[4] UPDIKE D P,KALNINS A. Axisymmetric behavior of an elastic spherical shell compressed between rigid plates[J]. Journal of Applied Mechanics, 1970, 37(3):635-640.

[5] GUPTA N K, SHERIFF N M, VELMURUGAN R. Experimental and theoretical studies on buckling of thin spherical shells under axial loads[J]. International Journal of Mechanical Sciences, 2008, 50(3):422-432.

[6] GUPTA N K, SHERIFF N M, VELMURUGAN R. Experimental and numerical investigations into collapse behaviour of thin spherical shells under drop hammer impact[J]. International Journal of Solids & Structures, 2007, 44(10):3136-3155.

[7] SHARIATI M, ALLAHBAKHSH H R. Numerical and experimental investigations on the buckling of steel semi-spherical shells under various loadings[J]. Steel Construction, 2010, 48(8):620-628.

[8] 马春生, 杜汇良, 张金换,等. 薄壁扁球壳在撞击载荷下的动态响应和吸能特性研究[J]. 振动与冲击, 2007, 26(1):4-7.

MA Chunsheng, DU Huiliang, ZHANG Jinhuan, et al. Thin shallow spherical shells in dynamic response under the impact load and energy absorption characteristics research [J]. Journal of Vibration and Shock, 2007, 26 (1):4-7.

[9] 张亚栋, 方秦, 李忠平,等. 某大型防护门结构计算分析[C]// 中国土木工程学会防护工程分会第五届理事会暨第九次学术会议. 长春， 2004.

[10] YIN H, WEN G, HOU S, et al. Crushing analysis and multiobjective crashworthiness optimization of honeycomb-filled single and bitubular polygonal tubes[J]. Materials & Design, 2011, 32(8):4449-4460.

Energy absorption property and optimization design of nested thin-wall spherical shells under axial impact

RONG Xiang1, DENG Anzhong2, LI Fei2, CHEN Chen3

(1.Material Science and Engineering, Logistics Engineering University, Chongqing 401311, China;2. Military Engineering and Management, Logistics Engineering University, Chongqing 401311, China;3.Logistics Information& Logistics Engineering, Logistics Engineering University, Chongqing 401311, China)

Considering the limitation in the energy absorption ability of a single small span thin-wall spherical shell, a new nested thin-wall spherical shell structure was designed and its dynamic response under axial impact was simulated by using a finite element software. The effect of the thickness of the outer spherical shell, the height and thickness of the inner spherical shell on mechanical properties and deformation modes under axial impact were analyzed. A response surface model was established based on the evaluation indexes of specific energy absorption (SEA) and peak crush load(PCL), taking the thickness of the outer spherical shell and the height and thickness of the inner spherical shell as test variables. Based on the response surface model, the test variables were optimized with the non-dominated sorting genetic algorithm NSGA-Ⅱ. Under different working conditions, the selection of the geometrical parameters was put forward. The results show that the geometrical parameters are of significant effects on the energy absorption characteristics. The response surface model is accurate and reliable. And the optimization method which has been verified by the finite element simulation is beneficial in engineering applications.

energy absorption; nested thin-wall spherical shell; response surface; genetic algorithm

国家自然科学基金(11372355);军队后勤重点科研计划(BY215J009)

2016-04-06 修改稿收到日期： 2016-08-09

戎翔 男，硕士，1992年生

邓安仲 男，博士，教授，1974年生

TH212；TH213.3

A

10.13465/j.cnki.jvs.2017.10.038