基于直纹曲面重构的铝合金薄壁件加工变形误差补偿方法*

樊建勋，徐仁乾，胡自化，秦长江，徐韬智

（1.海军驻阎良地区航空军事代表室，西安 710089；2.航空工业西安飞机工业（集团）有限责任公司，西安 710089；3．湘潭大学机械工程学院，湘潭 411105）

薄壁件作为数控切削加工的典型零件在航空、军工等尖端科学领域中应用广泛，如飞机结构件中的整体薄板以及发动机的涡轮叶片等。目前薄壁件已广泛采用数控侧铣加工工艺，由于这类零件具有结构形状复杂、刚度低、加工精度要求高等特点，在实际加工中极易产生加工变形，严重影响工件的加工精度以及表面质量[1]。

为有效控制加工变形误差，提高数控侧铣加工精度，国内外许多学者对加工变形误差的离线补偿技术进行研究。国外学者Depince等[2]对平头铣刀侧铣加工过程中刀具变形引起的误差进行了预测和补偿研究，并采用多步迭代的方法来计算最终补偿量。Zhang[3]、Huang[4]、Wei[5]等分别采用神经网络、递归方法和试验手段来修正刀具轨迹，以提高低刚度工件加工质量。Kvrgic[6]、Tung[7]、Peng等[8]开发了一些数控程序修改的软件，该软件通过修正NC代码的方法对加工变形误差进行补偿。国内学者武凯等[9]对薄壁腹板的加工变形规律进行分析并提出优化切削参数的方法来控制加工变形误差。詹友仁[10]通过对叶轮叶片加工变形误差补偿及侧铣刀轨计算方法的理论分析，利用铣削力预测模型及有限元仿真方法预测了叶轮叶片在铣削过程中的加工变形误差，在此基础上建立了基于加工变形误差补偿的叶轮叶片加工刀轨优化算法。刘雄伟[11]、孙越等[12]基于反变形思想，研究了误差补偿中的叶片模型重构和光顺问题，通过采用多次误差补偿方法，有效地提高了叶片的加工精度。王志刚等[13]运用有限元分析软件ANSYS对经典航空薄壁结构件的加工变形进行了分析，提出在精加工时在数控编程时让刀具在原有走刀轨迹中按照变形程度附加一个偏摆补偿的方法，大幅度消除让刀误差。

现阶段离线补偿方法主要从数控程序修改和刀具轨迹的直接修正两方面展开研究。本文转变传统研究思路，对基于直纹曲面重构的薄壁件加工变形补偿方法展开研究，该方法根据直纹面薄壁件加工变形的测量结果优选多次迭代补偿法；通过CAD逆向造型方法构造直纹补偿面间接对刀具轨迹进行修正，建立基于加工变形误差补偿的刀轨优化算法；最后开展直纹面薄壁件的数控铣削试验研究，以验证所建立的补偿方法的有效性。

理论基础

1 加工变形误差补偿原理

加工变形误差的补偿方法主要分为在线式和离线式两种，与在线式误差补偿法相比，离线误差补偿法对相关硬件要求较低，具有成本低，可操作性强的特点，故本文采用离线补偿法开展相关研究。加工变形误差的补偿主要是通过对加工过程中的铣削力进行精确预测，同时利用有限元方法分析得出加工变形，进而通过误差补偿方法对加工刀轨进行修正，从而达到对加工变形误差的补偿，加工刀轨补偿原理如图1所示。在图1中的刀位点j处，理论切触点位置为Xd，该点处的加工变形量为Ui，以及补偿修正后的切触点位置为Xc，3者之间的关系可由下式表示：

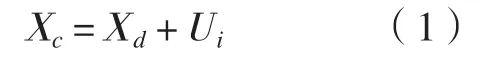
2 加工变形误差完全补偿法

完全补偿法是指每一加工切触点处的补偿量与该点加工变形量相等的补偿方式。加工变形误差完全补偿原理图，如图2所示。图2中以理论轮廓作为基准轴，若工件P点的变形值为Zi，则该点的补偿值为相对基准轴的对称点Zi'，从而完成变形误差的一次性完全补偿。单次加工变形误差补偿法虽然计算简单，但并没有考虑加工变形与误差补偿量的耦合关系。通过对刀位轨迹进行补偿后，新的刀位轨迹会使各个切触点的铣削条件发生变化，从而导致新的加工变形的产生，因此补偿后的实际切深与初始名义切深之间仍残余一定的加工变形误差，故单次加工变形误差补偿难以一次性将加工变形误差补偿到位。

3 多次加工变形误差迭代补偿法

多次加工变形误差迭代补偿法则考虑了加工变形与误差补偿量的耦合关系，采用分层迭代的方式对变形误差进行优化补偿。多次加工变形误差迭代补偿法原理如图3所示。

设刀位某一位置刀触点的初始变形值为δ0，对应的加工变形误差为λ0。进行第一次补偿后，由于铣削参数的变化而产生新的变形值为δ1，对应的加工变形误差为λ1，从而进行第二次补偿。以此类推进行迭代补偿，直到加工变形误差处于合理的加工精度范围内，则补偿终止。

4 直纹面成形方法

直纹面是由两条准线上具有相同u向参数的两点连接的直母线构成的。方程表示为：

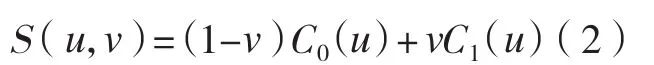
式中，C（0u）、C（1u）为具有相同参数u的两条准线，u为准线方向参数，v为直母线方向参数，u，v∈（0，1）。而直纹面又可分为可展直纹面和不可展直纹面两种类型，若直纹曲面上任意两条直母线在同一平面上，称为可展直纹面，即该曲面能平整地展开成一平面；反之，为不可展直纹面。

参照直纹面的定义利用CAD软件将两条准线上部分u向参数相同的两点用直线相连作为截面线，其构成的多截面曲面即为直纹面，而截面线的数量越多其直纹面的精度也越高。该成形方法可同时适用于可展直纹面和不可展直纹面。

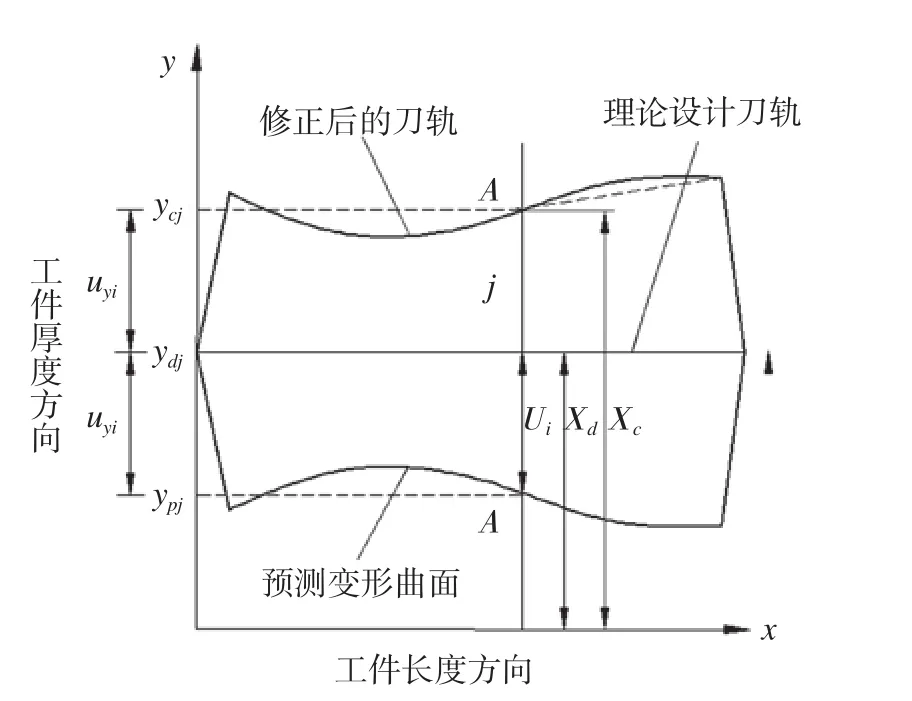
图1 加工变形误差补偿原理Fig.1 Compensation principle of machining deformation error

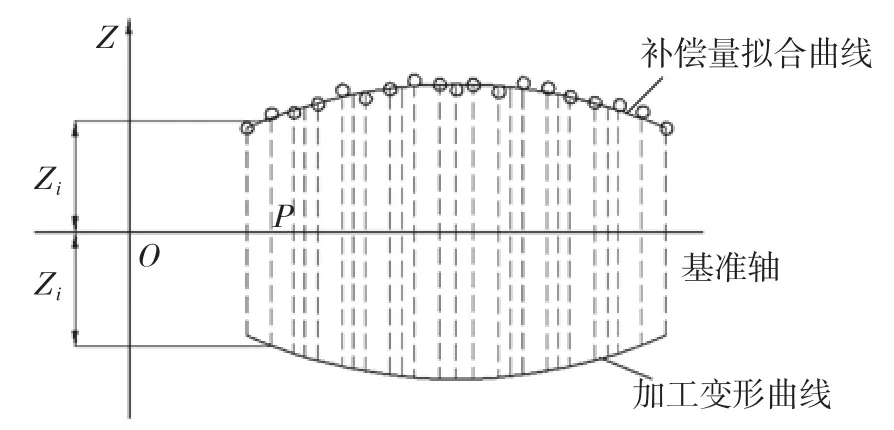
图2 加工变形误差完全补偿原理Fig.2 Complete compensation principle of machining deformation error

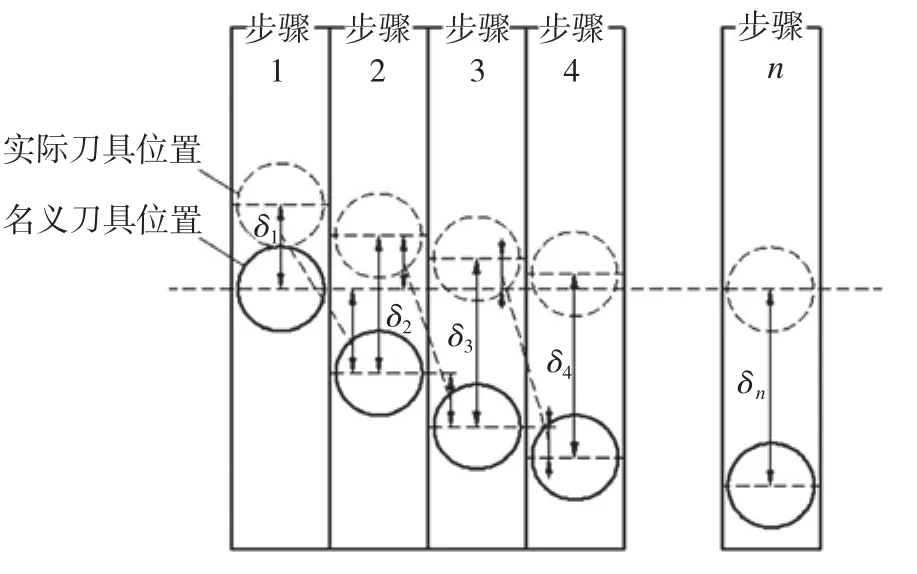
图3 多次加工变形误差迭代补偿原理Fig.3 Iteration compensation principle of multiple machining deformation error

加工变形补偿算法的建立

1 基于直纹面重构的薄壁件加工变形补偿策略分析

加工变形误差的补偿主要是通过对加工过程中的铣削力进行精确预测，同时利用有限元方法分析得出加工变形，通过误差补偿方法对加工刀轨进行修正，达到对加工变形误差的补偿。由于在薄壁件的铣削加工中影响铣削力的主要工艺参数有铣削速度vc、进给量f、轴向切深ap及径向切深ae。因此，本文通过设计正交试验，基于多元线性回归方法建立铣削力预测模型。根据金属切削原理，铣削力经验公式的一般形式为：

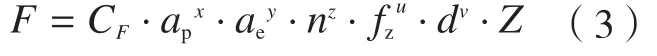
式中，CF为材料以及加工条件的相关系数，ap为轴向切深，ae为径向切深，fz为每齿进给量，n为主轴转速，d为刀具外径，Z为刀具齿数，x、y、z、u、v为各切削参数系数。

在实际加工中，所选取的刀具直径和齿数都是确定的，因此式（3）可简化为：

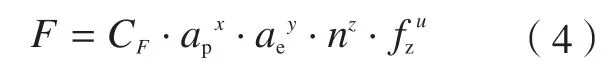
为提高薄壁件的加工精度，本文提出采用构造直纹曲面补偿面对刀具轨迹进行修正，进而建立基于加工变形误差补偿的刀轨优化算法。基于曲面重构的完全补偿法的原理，如图4所示。P1点为薄壁件直纹面某一铣削位置的刀触点，基于完全补偿法原理，若将该点变形误差作为补偿量并沿着刀触点的曲面法矢方向修正刀位轨迹时，则可获得补偿后的刀触点P1'。Pi'位置，以此类推可获取各个铣削位置补偿后的刀触点。Pi'（i=1，2，…，n）的位置，具体表达式为：

式中，βi为补偿偏置量，N（u，v）为曲面S上对应的单位法矢，即：

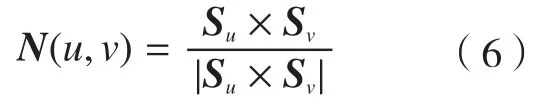
式中，Su和Sv分别表示曲面S关于u和v的偏导向量。

补偿后的离散刀触点还不足以反映出外轮廓特征的变形规律，此时需要通过逆向点造型构造补偿面，并利用CAM软件重新生成APT代码，最终完成薄壁件直纹面加工变形补偿。在进行逆向点造型构造补偿面时，由于本文的研究对象为薄壁件直纹面，且现阶段多数商业CAM软件中多轴侧铣加工数控自动编程只针对直纹面，故将补偿后的刀触离散点进行直纹化逼近，其生成的直纹面即可满足CAM软件数控自动编程条件。参照直纹面的成形方法，重构直纹补偿面的关键环节在于截面线的构造，假设对原直纹面u向某条直母线上v向各切触点进行补偿偏置，由于各点补偿方向和距离各不相同，故补偿后的离散点并不在一条直线上，可将这些离散点利用最小二乘法进行空间线性拟合[13]，已知空间直线的标准方程为：

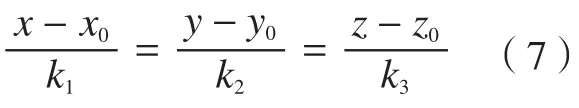
化简可得:

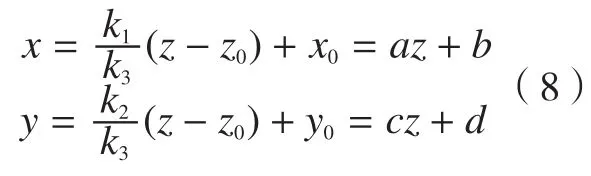
式中，a=k1/k3，b=x0-k1z0/k3，c=k2/k3，

空间直线可看作方程所表示的两个平面的交线，故可对这两个方程进行拟合，由于拟合方程所求的近似值和实际值存在残差，其残差的平方和为：

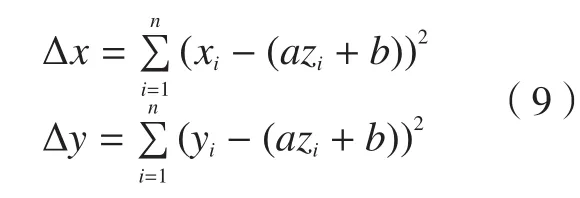
式中，xi、yi、zi（i=1，2，…，n）为各刀触点补偿偏置后的坐标，为了求得残差的最小值对上式中a、b、c、d偏导并令其全部为零：

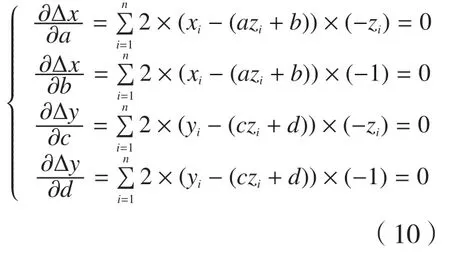
依据式（10）可求得：

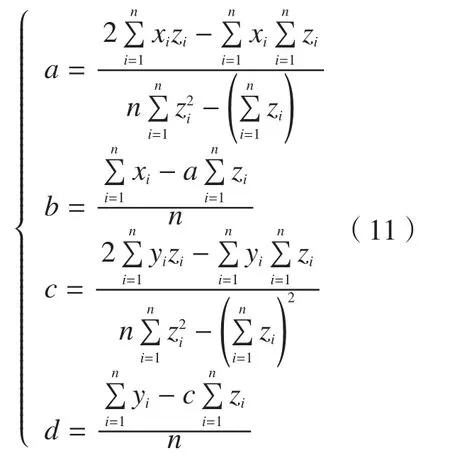
图5为补偿后离散点拟合直线示意图，依次类推可将v向各补偿后离散点拟合而成的直线作为截面线，将截面线坐标导入CAD软件构造直纹补偿面，利用CATIA软件多截面重构的补偿直纹面可直接用于后续刀位计算及数控编程。

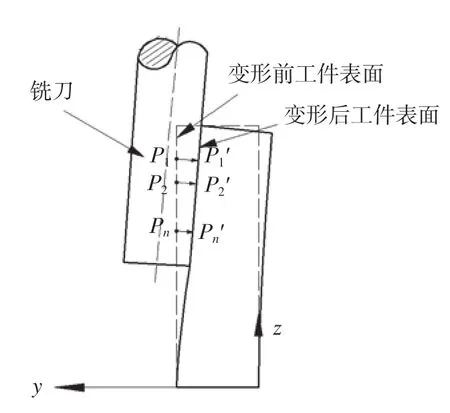
图4 基于曲面重构的完全补偿法原理Fig.4 Principle of complete compensation method based on surface reconstruction

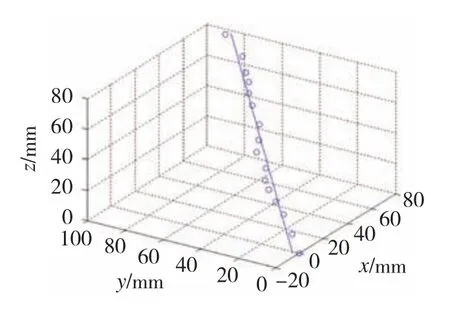
图5 补偿后离散点拟合直线示意图Fig.5 Fitting line diagram of discrete point after compensation

2 基于直纹面重构的薄壁件加工变形补偿迭代算法的建立

根据多次迭代加工变形误差补偿方法以及直纹面重构原理，建立基于直纹曲面重构的薄壁件加工变形补偿算法的步骤如下：

（1）设薄壁件直纹面加工层数为m，每一层侧铣加工刀位点数为n。设第j（j=1，2，…，m）层第i（i=1，2，…，n）个曲面刀位点名义径向切深为，根据所建立的铣削力模型计算出该点的铣削力

（2）将计算获取的铣削力代入有限元模型可预测出外轮廓曲面在第j层第i个刀位点对应的切触点的变形值根据加工变形误差补偿原理可计算得出沿该点曲面法向的补偿量

（3）将第j层第i个切触点沿该点曲面法向进行补偿偏置，可得到补偿后的切触点。重复上述3个子步骤则可计算得出补偿后的第j+1层所有切触点，并将该层所有补偿后的切触点经过曲面拟合得出补偿面。

（4）利用步骤（3）中所拟合重构的补偿面经CATIA数控编程软件进行第j+1层的虚拟加工，计算出新的名义径向切深为，以此获取新的铣削力与加工变形量。重复上述4个子步骤进行循环迭代计算，直到该层切触点的最大加工变形误差处于合理的加工精度范围内，此时可获得最终优化后的加工刀轨。

上述算法中参数可由递推公式（12）进行推导，该公式可根据多次迭代补偿法的相关原理及计算过程归纳得出。

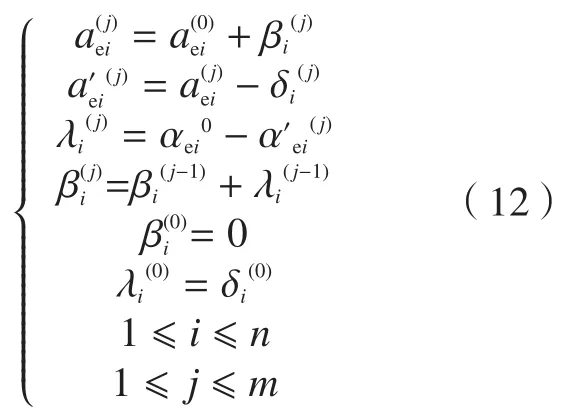
式中，表示第j次补偿第i个点的实际径向切深，且因为以及表示初始加工表面的第i个切触点的名义径向切深以及变形量，可由有限元计算获取，从而式（12）可进一步简化为：

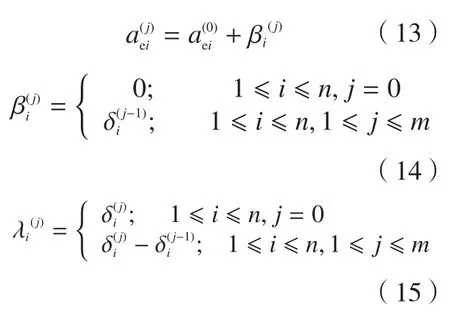
将式（13）～（15）的计算结果带入算法中，可最终建立肋板类零件外轮廓特征加工变形误差补偿刀轨优化算法，图6为该算法具体流程图。

试验验证

为了验证本文所建立的加工变形补偿方法及算法的正确性及有效性，本文以直纹面薄壁件为加工对象。该直纹面薄壁件毛坯的尺寸长 × 宽 × 高 为： 160mm×5.5mm×160mm。坐标系原点位于零件顶端面的中点，材料为铝合金7075-T651，加工设备为HERMLE-C30U五轴数控加工中心。加工刀具为φ20mm整体硬质合金圆柱立铣刀（AL-2RL-D20.0R3.0-AIR），主要参数如表1所示。

为建立铣削力预测模型，选取影响铣削力的4个主要因素即主轴转速n、进给量fz、径向切宽ae、轴向切深ap，每个因素取4个水平，设计了L16（44）的切削力正交试验。并通过选用瑞士KISTLER公司Kistler 9441B型多通道测力仪、Kistler 5070型放大器、台式计算机来构建铣削力检测平台。正交试验方案和收集的3向平均力数据如表2所示。

进而求得三向铣削力关于径向切深ae、轴向切深ap、主轴转速n、每齿进给量fz的线性回归方程，铣削力预测模型如下：

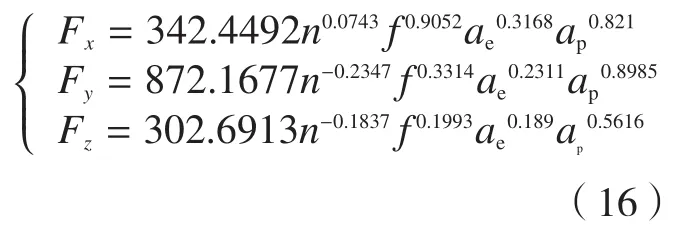
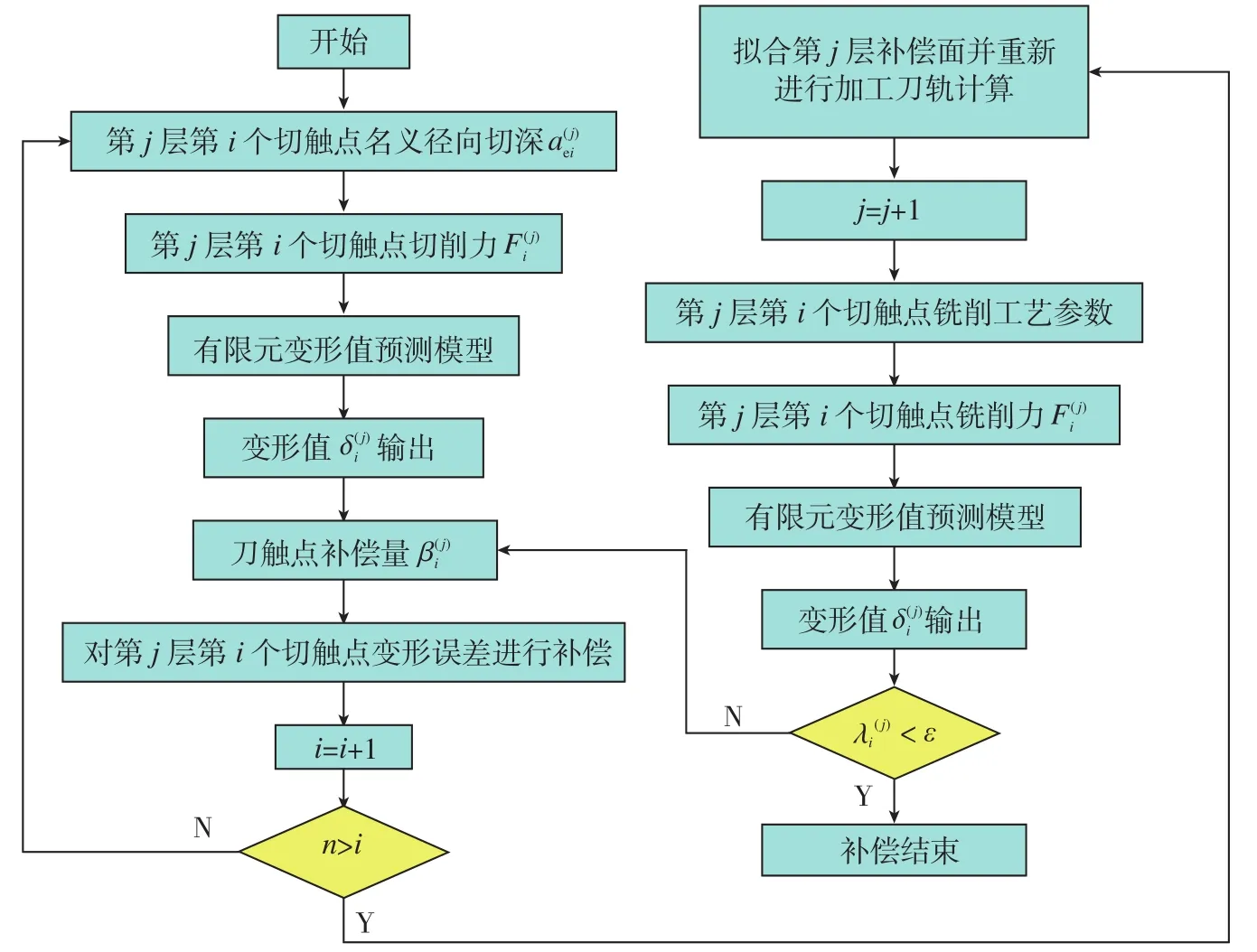
图6 加工变形误差补偿多次迭代算法流程图Fig.6 Flow chart of iterative algorithm for machining deformation compensation

基于有限元分析软件ANSYS建立直纹面薄壁件的有限元模型，由ANSYS分析出所有刀位点的变形值之后，根据加工变形误差补偿和曲面重构原理，基于CATIA软件对薄壁直纹零件进行刀轨规划，然后分别开展未采用补偿方法、1次完全补偿和1次迭代补偿的3种侧铣精加工方案。精加工时刀具采用φ20mm的整体硬质合金立铣刀，切削参数：主轴转速为10000r/min，轴向切深为1mm，径向切深为0.5mm，每齿进给量为0.06mm/z。由于加工零件平面符合直纹面定义，测量点分别沿x、z两向均匀分布，间隔为5mm，且考虑到直纹薄壁件在x向和z向的变形非常小，不到y向变形的1/10，故本文试验采用三坐标测量仪只对y向变形误差进行测量。

在铣削工程中，零件两端的约束少于中间的约束，故未补偿的直纹面薄壁件的加工变形误差呈现“两边大，中间小”的分布规律，且采用压板装夹固定，加工时薄壁件顶端的变形最大，然后沿底部方向逐渐减少。根据加工变形误差测量结果，分别从x和z两个方向进行对比。图7所示为沿工件x方向z=3mm处补偿前后加工变形误差测量值对比图，第二次迭代补偿后的误差平均值为0.074mm，与未补偿时的误差平均值0.255mm相比减少了70.98%，与第一次完全补偿后的误差平均值0.122mm相比减少了39.34%，可见随着迭代次数的增多，加工变形误差下降更为明显，且各个测量点沿x方向的误差更为接近，说明在x方向的补偿效果较为显著。

图8所示为沿工件z方向x=78mm处补偿前后加工变形误差测量对比图，由于零件底部的刚度大于顶部刚度，故未补偿的薄壁矩形板的加工变形误差随着z值的增加逐步增大。第二次的迭代补偿后的误差平均值为0.037mm，与未补偿时的误差平均值0.174mm相比减少了78.74%，与第一次完全补偿后的误差平均值0.086mm相比减少了56.98%，可见随着迭代次数的增多，加工变形误差下降更为明显，且各个测量点沿Z方向的误差分布更为均匀，说明在Z方向的加工变形误差补偿同样取得了较好的效果。

由此可知，本文所建立的基于薄壁件直纹曲面重构的加工变形补偿算法有效地控制了直纹面薄壁件的变形误差，达到了提高直纹面薄壁件加工精度的目的，是一种控制直纹面薄壁件加工变形误差的可行方法。

表1 φ20mm整体硬质合金铣刀主要几何参数

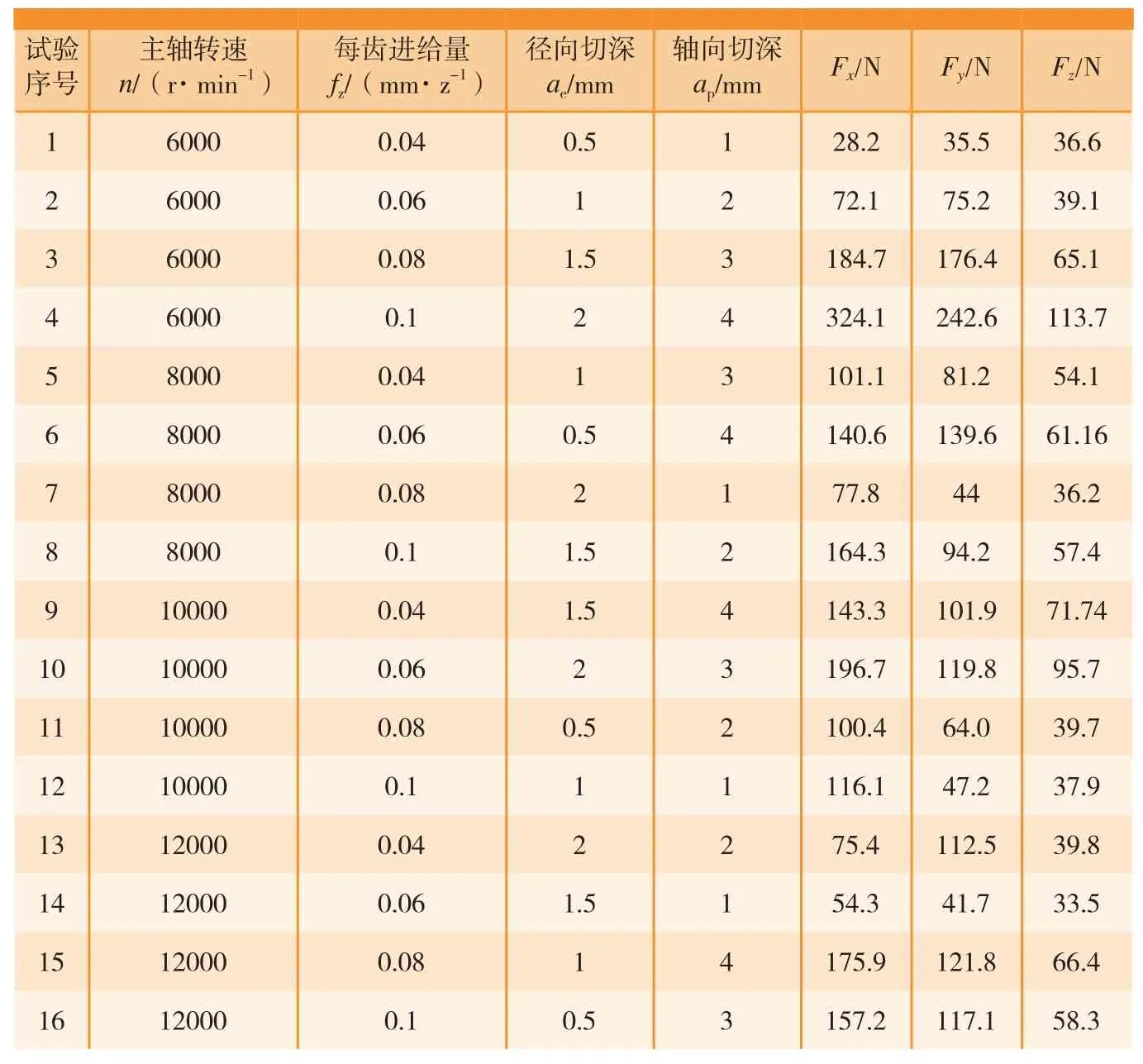
表2 铣削力正交试验方案及3向平均力结果

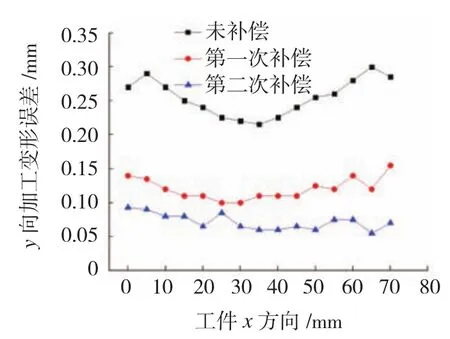
图7 z=3mm变形误差对比Fig.7 Comparison of deformation error of z=3mm

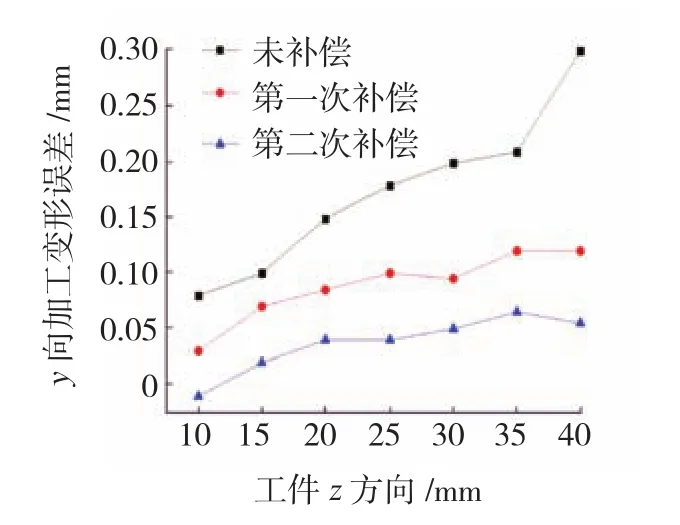
图8 x=78mm变形误差对比Fig.8 Comparison of deformation error of x=78mm

结论

（1）针对直纹面薄壁件在数控侧铣中的加工变形问题，依据加工变形误差补偿和直纹面成形理论，提出了基于直纹面重构的薄壁件加工变形误差补偿策略，该策略将原表面补偿偏置后离散点拟合重构成新的直纹面，并代替原表面进行侧铣加工，并在此基础上建立多次迭代补偿算法以进一步减少加工变形误差。

（2）为验证本文所建立的加工变形补偿方法及迭代算法的正确性及有效性，本文以直纹面薄壁件为加工对象开展了相关验证试验，并对X及z方向加工变形误差分布规律进行分析。结果表明，随着迭代次数的增多，零件的加工变形误差有了明显的下降，且误差分布更为均匀，补偿效果也更为明显，从而证明了本文所建立的基于直纹面重构的薄壁件加工变形误差补偿方法有效可行。

参 考 文 献

[1]何宁,杨吟飞,李亮,等.航空结构件加工变形及其控制[J].航空制造技术,2009(6):32-35.HE Ning, YANG Yinfei, LI Liang, et al.Machining deformation of aircraft structure and its control[J]. Aeronautical Manufacturing Technology, 2009(6):42-47.

[2]DEPINCE P, HASCOET J Y. Active integration of tool deflection effects in end milling[J]. International Journal of Machine Tools and Manufacture, 2006,46(9):945-956.

[3]ZHANG Y, YANG J, JIANG H.Machine tool thermal error modeling and prediction by grey neural network[J]. The International Journal of Advanced Manufacturing Technology, 2012, 59(9): 1065-1072.

[4]HUANG T, CHANG S, DING C, et al.Improvement of residual error in hydrodynamic polishing by recursive error compensation strategy[J]. Microelectronic Engineering, 2012,93:27-34.

[5]WEI Z, WANG M, CAI Y, et al. Form error estimation in ball-end milling of sculptured surface withz-level contouring tool path[J]. The International Journal of Advanced Manufacturing Technology, 2013, 65(1): 363-369.

[6]KVRGIC V, DIMIC Z, CVIJANOVIC V, et al. A control algorithm for improving the accuracy of five-axis machine tools[J].International Journal of Production Research,2014,52(10):2983-2998.

[7]TUNG C, TSO P L. A generalized cutting location expression and post processors for multi-axis machine centers with tool compensation[J]. The International Journal of Advanced Manufacturing Technology,2010, 50(9-12): 1113-1123.

[8]PENG F, MA J, WANG W, et al. Total differential methods based universal post processing algorithm considering geometric error for multiaxis NC machine tool[J]. International Journal of Machine Tools and Manufacture, 2013,70: 53-62.

[9]武凯,何宁,廖文和,等.薄壁腹板加工变形规律及其变形控制方案的研究[J].中国机械工程, 2004, 15(8): 670 -674.WU Kai, HE Ning, LIAO Wenhe, et al.Study on machining deformations and their control approaches of the thin-web in end milling[J]. China Mechanical Engineering, 2004, 15(8):670 -674.

[10]詹友仁.离心叶轮五轴加工刀轨与工艺参数优化方法与试验研究[D].湘潭:湘潭大学, 2012.ZHAN Youren. Research on optimization method of tool paths and process parameters and experiments for five-axis NC milling centrifugal impeller[J]. Xiangtan: Xiangtan Universtity,2012.

[11]刘雄伟,李杰光,赵明,等.航空发动机薄壁叶片加工变形误差补偿技术研究[J].机械设计与制造,2009(10):175-177.LIU Xiongwei, LI Jieguang, ZHAO Ming, et al. Research on the compensation of deformation error in NC machining of thin-walled blades[J]. Machinery Design & Manufacture,2009(10):175-177.

[12]孙越.叶片类扭曲曲面薄壁件铣削加工变形仿真与实验研究[D].沈阳:沈阳航空航天大学, 2013.SUN Yue. Simulation and experiment for the twisted thin-walled part of blades of machining deformation[D]. Shenyang: Shenyang Aerospace University,2013.

[13]王志刚,何宁,武凯,等.薄壁零件加工变形分析及控制方案[J].中国机械工程, 2002,13(2): 114-119.WANG Zhigang, HE Ning, WU Kai, et al.Analysis and control methodology of machining deformation of thin-walled part[J]. China Mechanical Engineering, 2002, 13(2): 114-119.