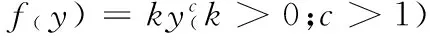随机机器故障下加工时间可控的并行机鲁棒调度
王建军,刘晓盼,刘 锋,王杜娟
(1. 大连理工大学系统工程研究所,辽宁 大连 116023;2. 东北财经大学管理科学与工程学院,辽宁 大连 116025)
随机机器故障下加工时间可控的并行机鲁棒调度
王建军1,刘晓盼1,刘 锋2,王杜娟1
(1. 大连理工大学系统工程研究所,辽宁 大连 116023;2. 东北财经大学管理科学与工程学院,辽宁 大连 116025)
现实生产环境中经常面临随机机器故障,造成初始调度方案性能恶化。针对并行机环境下工件加工时间可控,提出内外两层嵌套式的鲁棒调度策略,旨在降低随机机器故障造成的成本损失期望,干扰发生后通过局部修复实现跟初始计划的匹配。内层建立非线性0-1混合整数规划模型,通过二次锥化方法来求解初始调度方案在随机机器故障干扰情景下的成本损失期望。外层设计基于工件柔性和机器不可用概率的排序算法;由于问题内在的复杂性,利用遗传算法优化工件柔性参数,进而增强初始调度方案的鲁棒性。最后设计随机仿真实验,分别验证了在机器故障所造成的单位时间扰动成本不同时和机器维修水平不同时所提鲁棒调度策略的有效性。
鲁棒调度;并行机;加工时间可控;随机机器故障;匹配
1 引言
制造企业实际生产过程中往往面临诸多不确定性因素,如机器故障、订单变更等干扰事件,这些干扰事件常常造成初始调度方案执行不畅、效率低下、甚至不再可行[1]。面对不确定性事件造成的负面影响,如何制定出具有较强抗干扰能力的鲁棒调度方案已成为生产调度干扰管理领域研究的一个热点问题[2]。
随机机器故障是生产加工系统中最为常见和重要的一类干扰事件[3]。目前,在随机机器故障干扰下的鲁棒调度问题已受到学术界的广泛关注[4-9,12-13]。如针对加工时间固定的情形,通常采用的鲁棒调度方法为插入空闲时间,即在相邻工件之间插入一段缓冲时间来吸收随机机器故障造成的扰动。该方法首次由Mehta等[4]提出,并利用该方法有效降低了车间作业环境下机器故障导致的工件最大延迟时间。基于插入空闲时间的思想,尹文君等[5]采用双子树结构编码的遗传编码系统,使工件排序和空闲时间插入过程有效融合,获得拖期性能和预测能力较好的单机鲁棒调度。李巧云等[6]则提出通过阈值来控制空闲时间插入与否,使得空闲时间得到充分利用。同样是单机环境,Liu 等[7]在优化初始调度性能的基础上,考虑干扰发生后新旧计划偏差,从而转化为双目标问题,并提出两阶段多种群遗传算法求解。而Al-Hinai等[8]将问题扩展到柔性作业车间,并设计混合遗传算法进行了求解。虽然插入空闲时间能够吸收机器故障造成的负面影响,使初始调度方案具有较好的鲁棒性,但该方法往往会造成机器低效率利用[9]。
现实中机器资源往往是有限的,而且工件加工时间可以通过增加成本方式压缩控制[10],此时插入空闲时间则需要增加额外的压缩费用而不再适用。针对加工时间可控的情形,Akturk等[11]在并行机环境下通过压缩工件加工时间的方式,使得某一时刻后新旧加工时间表能够匹配,从而有效降低了机器故障带来的扰动。同样是并行机环境,Gurel等[12]考虑到在扰动时间限定条件下,不同的初始加工排序会产生不同的压缩成本。采用将柔性较好,即吸收干扰能力较强的工件安排在机器不可用概率较高时间段的方式进行工件排序,有效降低了因机器故障而增加的压缩成本,并在各机器故障发生时刻和维修时间服从相同分布情况下获得鲁棒性较好的初始调度方案。Gurel等[12]中的排序策略相同,刘锋等[13]研究了单机环境下的初始加工时间表制定问题,并通过遗传算法确定柔性参数的方式对工件柔性度量进行了改进。
除上述文献在初始调度方案制定时,考虑不确定性因素,从而获得抗干扰能力较强的鲁棒调度外;在执行过程中制定有效的动态调度也可以提高调度的鲁棒性[14]。Tang Lixin等[15]研究了炼钢-连铸生产过程中发生随机干扰事件后的动态调度问题,通过改进差分进化算法对加工时间表重新优化排序。实际中调度方案制定往往是多目标决策,Felix等[16]针对油轮在运集和配送地点处的动态调度问题,就运输成本最小化和服务水平最大化两个目标,利用改进多目标蚁群优化算法获得较好的有效前沿解。与前者调度方案生成不同,Shen Xiaoning等[17]研究了柔性作业车间下的动态调度问题,提出基于预测-反应式的多目标进化算法,并结合决策者偏好建立数学模型来确定调度方案。
由文献综述可知,第一,加工时间可控情形下的鲁棒调度研究相对较少且成本损失仅考虑了压缩费用,并未考虑因“中断-重复”操作造成的资源浪费和给其它生产活动造成的损失,而该些费用普遍存在于生产实践[18]。第二,虽然在制定鲁棒调度中应用到机器故障概率分布信息,但未考虑各机器由于进厂日期、使用生命周期及历史磨损程度不同等原因而导致的故障发生概率及其分布函数的差异性[19]。基于以上两点研究不足,本文针对最一般平行机环境——并行机下机器加工能力有限且工件加工时间可控问题,提出内外两层嵌套式的鲁棒调度策略,旨在有效降低随机故障给生产加工系统带来的成本损失期望,获得具有鲁棒性的初始调度方案。
2 问题描述
如图1所示,机器发生故障后考虑“中断-重复”操作,即被机器故障强制中断加工的工件需要重新加工[13]。因机器故障和“中断-重复”操作使机器可用加工时间减少,为完成加工任务而需要压缩未完工工件的加工时间,同时可能造成机器工件的重新分配[22]。在此过程中考虑系统成本损失最小化。一方面是与调度本身相关的损失ΔC,主要包括“中断-重复”造成的资源浪费和加工时间压缩所增加的成本;另一方面是机器故障给其它相关生产活动造成的损失h·ΔT,其中ΔT为各机器扰动时间段之和,h为单位时间扰动给其它相关生产活动造成的损失。而以系统成本损失最小化为目标的重调度模型(RSM)将在4.2节详细阐述。

图1 初始调度方案与局部重调度方案甘特图
本文的研究目的是获得具有鲁棒性的初始调度方案,降低随机机器故障造成的系统成本损失期望。常见的鲁棒性度量是实际调度性能与计划调度之间偏差的期望指标。然而故障发生时刻和维修时间在未发生前都是未知[7],因此根据机器发生故障的概率及其概率分布信息来模拟机器故障发生的情景,鲁棒性度量则采用调度性能期望[23-24]。此处为系统成本损失期望:E(ΔC+h·ΔT),其对应决策者为风险中性类型。系统成本损失期望越小,则代表初始调度方案鲁棒性越好。
3 机器工件分配模型
为获得鲁棒调度,首先是以加工成本最小化为目标确定机器工件的分配,即确定每台机器所要加工的工件以及各工件加工时间的压缩量。定义0-1变量xij,若工件j在机器i上加工则xij=1,否则xij=0。连续变量yij是工件j在机器i上加工时的加工时间压缩量。从而机器工件分配模型可以用以下非线性0-1混合整数规划模型表示:
(1)
uijxij≥yij≥0,i=1,…,m,j=1,…n
(2)
(3)
xij∈{0,1},yij∈R+,i=1,…,m,j=1,…,n
(4)
其中约束(1)保证分配到机器i上的工件加工时间之和不超过机器可用加工时间段Di;约束(2)表示只有工件j在机器i上加工,即xij=1时,加工时间pij才可能被压缩且压缩量满足0≤yij≤uij;约束(3)表示各工件只能在一台机器上加工;约束(4)是对变量xij,yij的取值范围限制。
当模型中uij=0时模型MJ0为一般意义上的指派问题,非线性压缩成本函数f(y)=kya/b使模型求解难度加大,通过文献[20]可知,上述数学模型为NP难问题。即使非线性函数为二次函数时利用现有商业软件求解较大规模的问题也具有一定的挑战性。为了有效求解该问题,首先引入变量tij将非线性目标转换为约束条件,如模型MJ1所示:
(5)
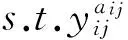
(5′)
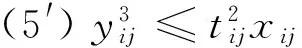
此时便可利用ILOGCPLEX12.4版本求解器进行建模求解,其有效性已在文献[20]中得以证明。
4 工件次序确定模型
在确定机器工件分配后,进一步需要确定每台机器上的工件加工次序。为此,设计了如图2所示内外两层嵌套结构的工件次序确定模型,内层结构主要用来计算初始调度方案的鲁棒性度量,即系统成本损失期望E(ΔC+h·ΔT);外层结构则是对初始调度方案的优化。该模型由初始调度模块、预案反应模块、遗传优化模块三个子模块构成。首先调用初始调度模块,将柔性较好的工件安排在机器不可用概率较高时间段,从而由工件柔性度量转化为工件加工次序;然后调用预案反应模块,计算给定工件加工次序在N种干扰情景下的系统成本损失期望;最后通过遗传算法模块优化工件柔性度量,进而达到优化工件加工次序,增强鲁棒性的目的。上述三个子模块的具体实现将在下面分别阐述。

图2 工件次序确定模型
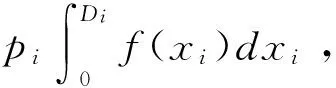
第二步则依据机器i的故障发生时刻及维修时间概率分布情况,依概率随机产生ni次干扰事件。
4.1 初始调度模块
初始调度模块主要是基于机器不可用概率分布函数,将柔性较好的工件安排到机器不可用概率较高的加工时间段,制定出初始加工时间表。其中机器不可用概率是指在t时刻或之前发生机器故障而导致t时刻机器不可用的概率。
(1)工件柔性度量指标及计算
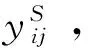
指标1:工件剩余可压缩量wj,计算公式为:
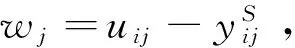
指标2:压缩成本函数的平均坡度Δj,反映工
件进一步压缩的过程中平均单位压缩成本。该值越小,压缩成本越小,柔性越好。计算公式为:
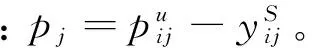
指标5:工件在机器间转移的最小成本LBj,设λi1和λi2分别表示机器i1和i2上工件的一阶导数,即工件边际压缩成本。则工件从机器i1转移到机器i2上加工所发生的转移成本为:
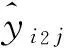
机器间转移成本越小,干扰发生时工件移到其它机器上加工所付出代价越小,即柔性越好。由于本文所研究环境为并行机,因此最小转移成本为:
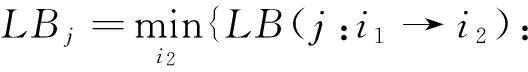
以上五个柔性指标分别从不同角度反映工件柔性,根据与工件柔性正负向关系,采用线性加权方式对工件柔性进行度量。柔性参数αi∈[0,1],将通过4.3中遗传优化模块进行确定和优化。
(2)机器不可用概率分布函数
研究故障发生时刻及维修时间分别服从指数分布且不同机器故障分布函数不同的情况。记机器i发生故障的概率pi,故障发生时刻分别服从参数为λi的指数分布,进而可得生产加工车间故障发生时刻x所服从的概率密度函数为:
同时记加工车间的维修时间y服从参数为λy的指数分布,则由文献[12]可知在t时刻或之前发生故障而使t时刻出现机器不可用概率密度函数为:
下面给出机器不可用概率密度函数Pd(t)为单峰函数的简单证明。
首先,机器发生故障的概率密度函数fx(x)为多个指数分布函数线性加权和,因此可得fx(x)为单调递减函数,即单峰函数且在0处取得最大值。其次,根据文献[12]中引理3.2当fx(x)在[0,+∞)上为单峰函数且有最大值时,相应机器不可用概率密度函数Pd(t)在[0,+∞)区间也为单峰函数。因此可证机器不可用概率Pd(t)是单峰函数。
(3)基于机器不可用概率分布的工件排序算法
在确定工件柔性度量和机器不可用概率之后,需要将柔性较好的工件安排在机器不可用概率较高的时间段来确定各机器上工件加工次序。为此设计了如下工件排序算法,具体步骤如下:
步骤1:令ts=0,te=Di,同时将本机器上加工工件按照柔性从小到大的顺序依次排列。
步骤2:取柔性最小工件j及其加工时间pj,
分别计算当其排到左边和右边时的机器不可用概率,计算公式为:
步骤3:若Pleft 步骤4:检查是否还有剩余未安排工件,如果有则返回步骤2,否则结束。 4.2 预案反应模块 预案反应模块主要是计算机器故障给系统造成的成本损失。为了使系统成本损失最小,而对未完工工件进行局部重调度,使新旧加工时间表能够在某一时刻之后完全一致,并称这一刻为匹配点。进行局部重调度的工件集包括被机器中断加工工件和还未开始加工工件。它们需要重新确定加工机器xij和压缩量yij;此外引入0-1变量zj,当zj=1表示该工件的开始加工时间为所在机器的匹配时间点。此模块用到的参数定义如下: S:初始加工时间表 sj:S中工件j的开始加工时间 M*:发生故障的机器 t*:机器故障发生的时刻 d*:机器故障维修的时间 j*:因机器故障而中断加工的工件 J:需要进行重调度的工件集合J={j|sj≥t*或者j*} Ji:J的子集,机器i上需要重调度的工件集 Pj:表示同一台机器上开始加工时间可以作为匹配点的工件j及其之前的工件集; tj:工件j开始加工时间作为匹配点时,所在机器i上与原调度不一致的加工时间; 当i=M*时,tj=sj-t*; ei:机器i上最后加工工件的完工时间Di作为匹配点时,该机器上与原调度不一致的加工时间表长度; 当i=M*时,ei=Di-t*; di:机器i上可以利用的剩余加工时间; 当i=M*时,di=Di-(t*+d*); 机器故障发生后与初始调度方案相关的成本损失主要包括两方面。一方面是调度本身所造成的成本损失ΔC,主要包括重调度造成的压缩成本增加和“中断-重复”操作造成的资源浪费,即可表示为:ΔC=ΔC压缩费用+ΔC资源浪费。前者通过新旧调度方案压缩成本差计算,后者按照被中断工件的已完工比例来计算,如下所示: 另一方面则是由于新旧加工时间表不一致而给其它生产活动造成的损失。其中扰动时间段ΔT主要包括机器故障维修时间和因重调度而产生扰动时间;设单位时间扰动给其它生产活动造成的成本损失为h,则给其它生产活动造成的损失为: 综上所述,机器故障后给生产系统造成的成本损失为ΔC+h·ΔT。预案反应模块则是以最小化生产系统成本损失为目标函数建立重调度数学规划模型进行求解。具体模型可以表述为如下所示的非线性混合0-1整数规划: (RSM)min ΔC+h·ΔT (6) yij≤uijxij,i=1,…,m,且j∈J (7) (8) (9) (10) (11) (12) xij∈{0,1},yij∈R+,i=1,…,m,且j∈J (13) (14) 其中约束(6)保证在剩余可用加工时间内完成加工任务;约束(7)为压缩量限制;约束(8)保证工件只能在一台机器上加工;约束(9)表示各机器上的匹配点可能为未加工工件开始加工时间且如果是则只能有一点;约束(10)(11)(12)则表示各机器匹配点之后的工件及其压缩量保持不变;约束(13)(14)则是变量取值的约束。与机器工件分配模型MJ0相似,该模型目标函数中同样含有非线性函数;通过二次锥化处理后用ILOGCPLEX12.4软件进行求解,在此不再详述。 4.3 遗传优化模块 遗传优化模块主要是通过遗传算法对柔性度量 (1)编码。采用非负实数编码,种群个体用五维向量{α1,α2,α3,α4,α5}表示,其中αi取[0,1]间实数;初始种群由随机函数生成指定规模的五维向量构成。 (2)个体评价。在进化过程中对于任意个体{α1,α2,α3,α4,α5}。首先,根据4.1初始调度模块中柔性度量Fj公式计算出每个工件的柔性,并且按照该模块中工件排序算法来确定相应的初始加工时间表。然后,依概率产生N种的干扰情景,利用4.2预案反应模块中的RSM数学模型计算出每种干扰情景下的成本损失。最后,取N种干扰情景下的系统成本损失期望E(ΔC+h·ΔT)来评价该个体。该值越小证明初始加工时间表的鲁棒性越强,即个体的适应度也就越大。 (3)遗传操作。为了保存种群优良特性同时更新种群进行选择、交叉、变异操作。本研究中选择操作采用锦标赛制;交叉操作采用离散重组的方式进行;变异操作则是均匀变异算子。鉴于遗传操作属于经典研究内容且非研究重点,细节方面不做过多解释。 (4)终止条件。当进化到指定代数则终止算法, 图3 遗传算法流程图 本节通过数值算例来验证所提鲁棒调度策略有效性。在排序方法方面,与经典SPT规则对比;已有学者证明机器故障发生时刻服从指数分布时SPT规则能够最小化期望工作流时间[26],因而以此制定初始调度方案是一种应对随机机器故障较好的方法。在柔性度量方面,与Gurel等[12]提出的解析式柔性度量对比。同时为了验证鲁棒调度策略普适性,设计了两组实验算例。分别验证在机器故障对其它生产活动影响不同时和机器维修水平不同时的有效性。两组实验都是依概率产生50次干扰情景,遗传算法则采用15条染色体运行30代。 5.1 单位时间扰动成本不同时有效性检验 E[λ·ΔC+(1-λ)·ΔT] 当λ=0时,h=+∞表示其它生产活动对扰动时间非常敏感;因而调度自身所增加的成本可以忽略不计,目标函数则为E[ΔT]。当λ=1时,h=0表示机器故障对其它生产活动的影响可以忽略不计;成本损失仅仅是调度本身所造成的,目标函数则为E[ΔC]。除上述两种情况外,λ的取值根据实际生产中单位扰动时间的成本损失h确定。 本文采用将柔性较好工件安排在机器不可用概率较高时间段的方式进行排序。如图4所示与经典SPT规则比较,当λ在0~1间变动时,本文排序方法对应系统成本损失期望一直处于SPT排序方法下面。从而验证了所提排序方法有效性。 图4 本文排序方法与SPT规则系统成本损失误差棒图 同时与刘锋等[13]中的解析式柔性度量不同,本文利用遗传算法优化柔性参数的方式来确定工件柔性度量。因此就柔性度量方式上与刘锋等[13]中针对故障发生时刻和维修时间概率分布为Exp-Exp情况时所提出的五种解析式柔性度量对比。针对不同柔性度量,定义改进率指标R,计算公式如下所示,其中E(CSPT)和E(CF)分别表示在SPT规则和不同柔性度量下的系统成本损失期望。 表1 不同柔性度量下的改进率指标1/0.1Di(%) 表1为扰动系数λ在0~1区间变化时,各柔性度量的改进率指标R值。表2为50次干扰情景下扰动系数λ从0~1变化11次过程中系统成本损失期望的95%置信区间估计,以及比SPT规则成本损失较小的实验次数。 由表1和表2可见,本文所对应改进率指标R大于0,改进数量最多,置信区间上下界小于SPT从而验证了所提排序方法比SPT规则有效。同时与五种解析式度量相比,遗传算法确定柔性度量的方式改进率R较大,改进数量较多且置信区间偏小,从而验证了所提柔性度量方式的有效性。综上可知,无论单位扰动时间给其它生产活动造成的成本损失h为多少,所提鲁棒调度策略都能有效降低随机机器故障造成的成本损失期望。 5.2 机器维修水平不同时有效性检验 表2 系统成本损失期望95%置信区间和较SPT改进数量 表3为机器故障维修时间分别服从参数为1/0.1Di和1/0.15Di指数概率分布时,扰动系数λ取0.0,0.5,1.0时的改进率指标R值。表4则为在50次干扰情景下,机器故障参数与扰动系数组合的6次变化过程中系统成本损失期望的95%置信区间估计,以及比SPT规则排序系统成本损失较小的实验次数。在不同的机器维修水平下,本文改进率指标R值大于SPT和各解析式扰动度量,同时改进数量总体最多且系统成本损失期望的置信区间上下界最小。从而表明所提鲁棒策略在排序方法和柔性度量方式上分别比SPT排序和解析式柔性度量要好,从而验证了在不同机器维修水平下的有效性。 表3 不同机器维修水平下改进率指标R(%) 表4 系统成本损失期望95%置信区间和较SPT改进数量 5.3 结果分析 通过两组实验对比表明,在排序方法上与经典SPT规则对比,验证了将柔性较好的工件安排在机器不可用概率较高的时间段能够有效降低干扰发生后系统成本损失期望。排序方法相同的情况下,在柔性度量方面与解析式柔性度量方式对比,验证了遗传算法确定柔性度量的有效性。主要原因是各柔性指标是从不同角度来度量工件柔性的。例如工件剩余可压缩量是从时间的角度来度量柔性,该值越大表示能够使扰动时间段越小;而成本压缩函数的二阶导数则是从成本角度来度量工件柔性的,该值越小则压缩单位时间所付出的成本越小。因此当扰动时间段对其它生产活动的影响程度不同时,即单位时间扰动成本h发生变化时,工件各柔性度量指标参数也应做出调整。也就是说不存在唯一柔性度量对不同的目标函数均有效。而遗传算法确定柔性度量方式正是由于其能够根据目标函数来调整柔性度量,从而保证了该方法的有效性。 本文在并行机环境下,针对机器加工能力有限且工件加工时间可控情况中随机机器故障问题。提出内外两层嵌套式的鲁棒调度策略,内层结构通过建立非线性0-1混合整数规划来计算初始调度方案在依概率产生的多种干扰情景下的成本损失期望;外层结构以成本损失期望为个体评价指标,通过遗传算法来优化工件柔性参数进而提高初始调度方案鲁棒性。 通过数值实验表明:(1)在排序方法上与经典的SPT规则对比,将柔性较好的工件安排在机器不可用概率较高时间段的排序策略使得系统成本损失期望更低;(2)在柔性度量上与解析式柔性度量对比,通过遗传算法确定柔性度量的方式平均改进率指标较高;(3)在机器故障对其它相关生产活动影响不同时和机器维修水平不同时,鲁棒调度策略同样具有有效性。 本研究有助于企业制定鲁棒性较好的初始调度方案,使机器故障发生给生产加工系统造成成本损失期望最小。未来进一步的研究方向包括两个方面,一是可以将所提鲁棒调度策略应用到其它类型的干扰事件应对研究中,二是可向鲁棒性替代度量及柔性参数确定方面深入研究和改进。 附录: 指标4证明 设L/ny0=θ,上式可变形为: 将(1+θ)a-1-aθ(1+θ)a-1按泰勒公式展开为: 即证C′(n)<0,因此当需要压缩的时间长度相同时,压缩工件越多则成本越少。又由于受匹配时间的限制,所以工件加工时间越短则放置的工件数量越多,进而使得工件柔性越好。 [1] 刘乐, 周泓. 一种常见干扰条件下的开放式车间重调度研究[J].管理科学学报,2014, 17(6): 28-48. [2]AhmadiE,ZandiehM,FarrokhM,etal.Amultiobjectiveoptimizationapproachforflexiblejobshopschedulingproblemunderrandommachinebreakdownbyevolutionaryalgorithms[J].Computers&OperationsResearch, 2016, 73: 56-66. [3]FazayeliM,AleaghaMR,BashirzadehR,etal.Ahybridmeta-heuristicalgorithmforflowshoprobustschedulingundermachinebreakdownuncertainty[J].InternationalJournalofComputerIntegratedManufacturing, 2016, 29(7): 709-719. [4]MehtaSV,UzsoyRM.Predictableschedulingofajobshopsubjecttobreakdowns[J].IEEETransactionsonRoboticsandAutomation, 1998, 14(3):365-378. [5] 尹文君, 刘民, 吴澄. 随机故障下单机鲁棒调度算法的遗传编程方法[J]. 清华大学学报(自然科学版), 2005, 45(1): 81-84. [6] 李巧云, 王冰, 王晓明. 随机机器故障下单机预测调度方法[J]. 系统工程理论与实践, 2011, 31(12): 2387-2393. [7]LiuLin,GuHanyu,XiYugeng.Robustandstableschedulingofasinglemachinewithrandommachinebreakdowns[J].InternationalJournalofAdvancedManufacturingTechnology, 2007, 31(7-8): 645-654. [8]Al-HinaiN,ElMekkawyTY.Robustandstableflexiblejobshopschedulingwithrandommachinebreakdownsusingahybridgeneticalgorithm[J].InternationalJournalofProductionEconomics, 2011, 132(2): 279-291. [9]XiongJian,XingLining,ChenYingwu.Robustschedulingformulti-objectiveflexiblejob-shopproblemswithrandommachinebreakdowns[J].InternationalJournalofProductionEconomics, 2013, 141(1): 112-126. [10]YangBibo,GeunesJ.Predictive-reactiveschedulingonasingleresourcewithuncertainfuturejobs[J].EuropeanJournalofOperationalResearch, 2008, 189(3):1267-1283. [11]AkturkMS,AtamturkA,GurelS.Parallelmachinematch-upschedulingwithmanufacturingcostconsiderations[J].JournalofScheduling, 2010, 13(1): 95-110. [12]GurelS,KorpeogluE,AkturkMS.Ananticipativeschedulingapproachwithcontrollableprocessingtimes[J].Computers&OperationsResearch, 2010, 37(6):1002-1013. [13] 刘锋, 王征, 王建军, 等. 加工能力受扰的可控排序干扰管理[J]. 系统管理学报, 2013, 22(4): 505-512. [14] 边志兴. 作业车间的模糊动态调度问题研究[J].中国管理科学,2008,16(S1):76-83. [15]TangLixin,ZhaoYue,LiuJiyin.Animproveddifferentialevolutionalgorithmforpracticaldynamicschedulinginsteelmaking-continuouscastingproduction[J].IEEETransactionsonEvolutionaryComputation, 2014, 18(2):209-225. [16]FelixTS,ShekharP,TiwariMK.Dynamicschedulingofoiltankerswithsplittingofcargoatpickupanddeliverylocations:Amulti-objectiveantcolony-basedapproach[J].InternationalJournalofProductionResearch, 2014, 52(24):7436-7453. [17]ShenXiaoning,YaoXin.Mathematicalmodelingandmulti-objectiveevolutionaryalgorithmsappliedtodynamicflexiblejobshopschedulingproblems[J].InformationSciences, 2015, 298:198-224. [18]LiuLe,ZhouHong.Ontheidenticalparallel-machinereschedulingwithjobreworkdisruption[J].Computers&IndustrialEngineering, 2013, 66(1): 186-198. [19]CuiWeiwei,LuZhiqiang,PanErshun.Integratedproductionschedulingandmaintenancepolicyforrobustnessinasinglemachine[J].Computers&OperationsResearch, 2014, 47: 81-91. [20]AkturkMS,AtamturkA,GurelS.Astrongconicquadraticreformulationformachine-jobassignmentwithcontrollableprocessingtimes[J].OperationsResearchLetters, 2009, 37(3): 187-191. [21] 李素粉, 朱云龙, 尹朝万. 具有随机加工时间和机器故障的流水车间调度[J]. 计算机集成制造系统, 2005, 11(10):1425-1429. [22] 刘锋, 王建军, 饶卫振, 等. 安装时间与次序相关的生产调度干扰管理研究[J].中国管理科学,2014, 22(1):45-54. [23]BonfillA,EspunaA,PuigjanerL.Proactiveapproachtoaddresstheuncertaintyinshort-termscheduling[J].Computers&ChemicalEngineering, 2008, 32(8):1689-1706. [24]WuSD,ByeonE,StorerRH.Agraph-theoreticdecompositionofthejobshopschedulingproblemtoachieveschedulingrobustness[J].OperationsResearch, 1999, 47(1): 113-124. [25]AlizadehF,GoldfarbD.Second-orderconeprogramming[J].MathematicalProgramming, 2003, 95(1):3-51. [26]AdiriI,BrunoJ,FrostigE,etal.Single-machineflow-timeschedulingwithasinglebreakdown[J].ActaInformatica, 1989, 26(7): 679-685. RobustSchedulingofUnrelatedParallelMachinesSubjecttoStochasticBreakdownsandControllableProcessingTimes WANGJian-jun1,LIUXiao-pan1,LIUFeng2,WANGDu-Juan1 (1.InstituteofSystemsEngineering,DalianUniversityofTechnology,Dalian116023,China; 2.SchoolofManagementScienceandEngineering,DongbeiUniversityofFinance&Economics,Dalian116025,China) Inevitable machine breakdowns always degrade the performance of the initial schedule in the practice. Considering the controllable processing time in unrelated parallel machines layout, how to generate a robust schedule to reduce the expectation value of the loss cost caused by the stochastic machine failures is studied. Therefore, a robust scheduling strategy of two nested layers is designed. In the inner layer, a nonlinear 0-1 mixed integer model is built to calculate the expectation of the loss cost. Because of the model’s complexity, it is translated into second-order cone constrains for solving efficiency. In the outer layer, sorting algorithm is designed based on the job’s flexibility and the probability of machine unavailability. Due to inherent complex and unstructured nature, genetic algorithm is used to optimize job’s flexible parameters, and to further enhance the robustness of the initial schedule. Through randomly generated numerical experiments, It shows that the proposed scheduling strategy is robust against different disturbance cost per unit time and different mean time to repair of machine breakdown. The research has a certain reference for sorting robust schedule and optimizing job’s flexible parameters. robust scheduling; unrelated parallel machines; controllable processing time; stochastic breakdowns; match-up 1003-207(2017)03-0137-10 10.16381/j.cnki.issn1003-207x.2017.03.016 2015-03-21; 2015-10-13 国家自然科学基金资助项目(71271039, 71672019, 71502026);教育部“新世纪优秀人才支持计划”项目(NCET-13-0082);中央高校基本科研业务费专项资金资助项目(DUT14YQ211) 王建军(1977-),男(汉族),河北保定人,大连理工大学系统工程研究所教授,博士生导师,研究方向:干扰管理、生产调度等,E-mail:.drwangjj@dlut.edu.cn. C939 A

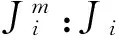
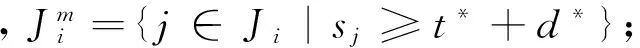
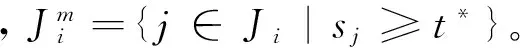
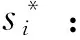
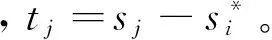
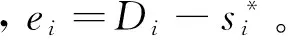
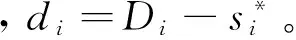
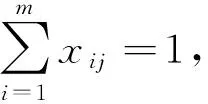
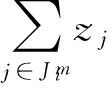

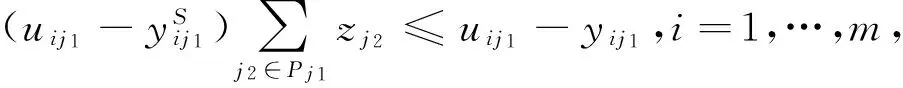
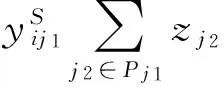
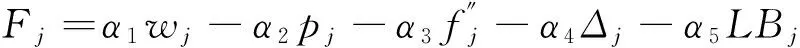
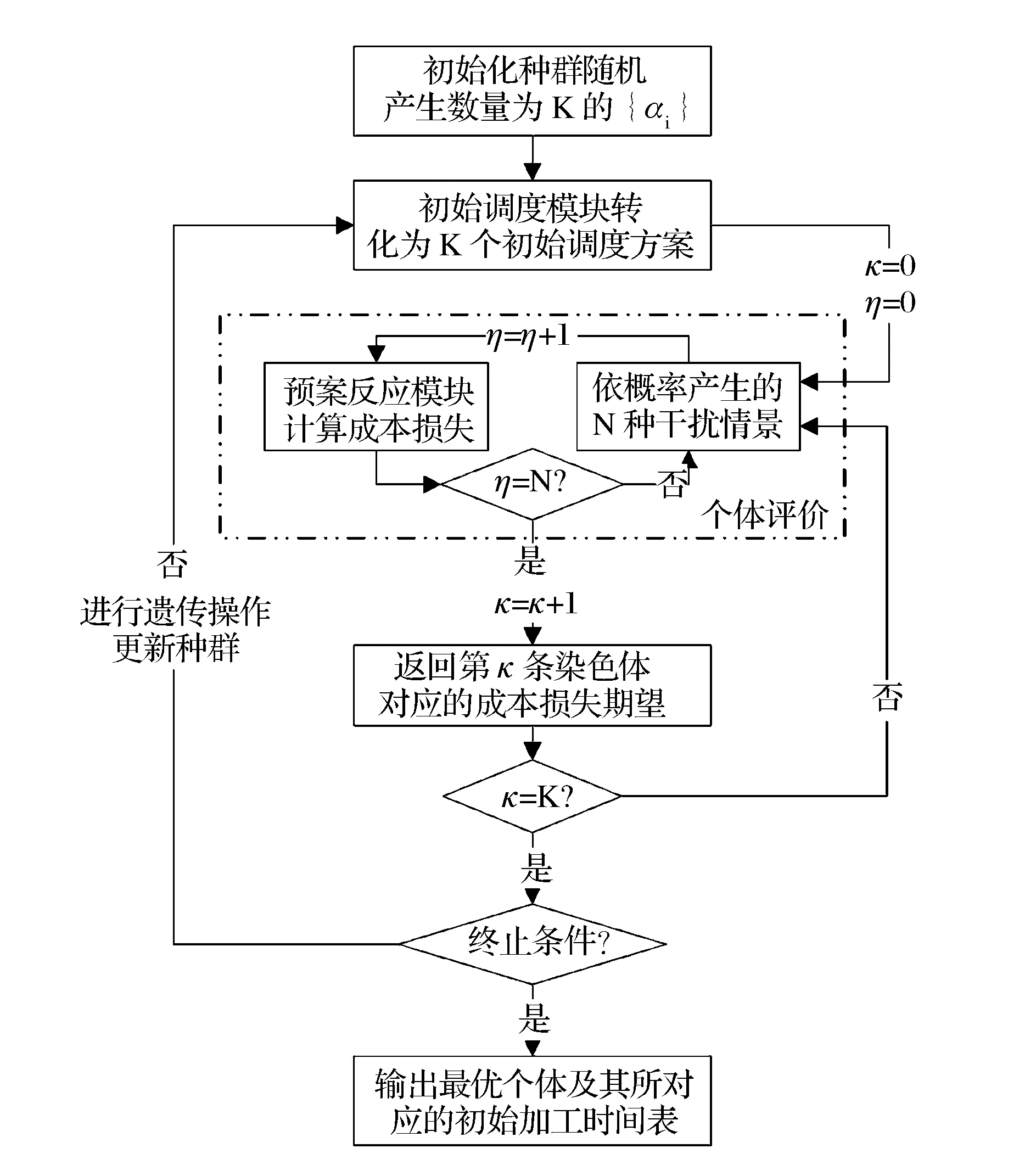
5 数值算例
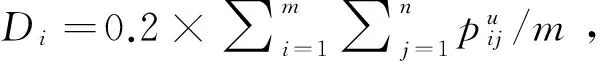

6 结语