基于用户社会关系的社交网络好友推荐算法研究
景 楠,王建霞,许 皓,卞亦文
(1.上海大学悉尼工商学院,上海 201899;2.安徽大学商学院,安徽 合肥 230601)
基于用户社会关系的社交网络好友推荐算法研究
景 楠1,王建霞1,许 皓2,卞亦文1
(1.上海大学悉尼工商学院,上海 201899;2.安徽大学商学院,安徽 合肥 230601)
社交网络中存在海量用户,如何有效推荐好友是社交网络可持续发展的重要环节,也是社交网络相关研究的重要主题。当前实践及现有研究往往基于用户的显性信息推荐好友,而忽略了用户之间的隐性社会关系;此外,显性信息往往不够完整且存在虚假信息问题。为有效实现好友推荐,本文提出了基于用户社会关系的好友推荐算法,并重点应用关联规则算法分析用户之间的隐含关联度,构造用户之间的网络有向图及关系转移矩阵;然后,结合关系转移矩阵与PageRank算法计算每个用户的分数,将分数较高的用户推荐给目标用户。在此基础上,本文引入用户影响力,提出综合考虑用户社会关系及用户影响力的PeopleRank算法。为验证算法的合理性和有效性,将本文所提出的两种算法与传统的社会过滤算法、PageRank算法进行对比分析。为此,本文抓取了Twitter社交网站上用户数据开展实验分析。实验结果显示本文所提出的算法具有较好的推荐效果,尤其是综合考虑用户社会关系及用户影响力的好友推荐算法在推荐准确率和推荐召回率上都有明显的优势。
社交网络;好友推荐;社会关系;影响力;PageRank算法
1 引言
社交网站的兴起改变了人们的交流方式,促进了沟通频率,并提高了沟通效率。网络用户主要通过社交网站关注新闻热点话题及感兴趣的人与事,而相关信息的获取主要来源于其所关注的人群[1]。对于用户而言,如果能够提供一些精选的用户,将能提升用户在社交网站中的体验和满意度。因此,社交网站中好友推荐应运而生。为有效推荐用户好友,推荐算法就成为重要的研究主题。
目前,国内外对于社交网站好友推荐算法的研究成果相对较少。从研究对象角度来看,现有的好友推荐算法主要基于社交网站用户的显性社交信息和显性社会关系[2]。显性社交信息包括用户的地理位置、标签信息、话题信息、文本信息。Zheng Yu等[3]将一个用户访问某个位置的次数作为对该位置的隐含评分,并利用该评分来计算用户之间的相似性,并以此进行好友推荐。胡江文等[4]提出了基于关联规则与标签的好友推荐算法,该算法首先挑选出与目标用户共同好友最多的用户集,然后通过计算目标用户和每个候选用户之间的标签相似度以推荐相似度最高的用户;然后设定初步推荐好友的权重,并进行打分,选取分数最高的用户进行推荐。于海群等[5]利用文本挖掘的相关技术和最小均方误差算法,把抓取的用户话题数据转化成用户偏好特征向量,用相似度度量方法计算用户之间的相似度以确定与用户话题偏好最相近的用户集,并完成用户的二级好友推荐。Weng Jianshu等[6]分别把每个用户发布的所有微博集成为一个文档,使用文档主题生成模型发现每个用户潜在感兴趣的主题。Chen Jilin等[7]采用向量空间模型表示用户所发布的微博文本,用Term Frequency-Inverse Document Frequency 技术提取用户的特征向量,计算用户特征向量之间的相似性,以此推荐相似性较高的用户。
基于显式社会关系的好友推荐基于用户的社会关系在不同的好友之间进行信息互联和好友推荐[8]。显式社会关系通常指社会网络用户的一级人脉,即直接关注关系。基于此类关系的主要算法包括社会过滤和PageRank算法。社会过滤算法基于分析隐含于用户每一位好友的信息准确地推荐好友,主要推荐与目标用户共同好友最多的用户[9]。舒琰等[10]认为微博平台上只通过对比粉丝人数而进行排名的方法不尽合理,其基于PageRank算法,以用户为节点,以用户关系为有向边,建立概率转移矩阵,计算微博用户的PageRank值。Weng Jianshu等[6]提出将用于网页排序的Page Rank 算法应用于社交网络计算用户的影响力,并向目标用户推荐影响力较大的用户。王平等[11]基于人人网的用户社会关系,应用好友分类和关系连接权重分类的方法解决好友过多和信息爆炸的问题。Chen Can等[12]认为用户的影响力与用户页面和用户交互之间的链接结构有关,利用用户之间的社会关系计算用户之间的关系强度构建转移矩阵,结合PageRank算法计算用户的影响力,从而推荐出影响力较高的用户。向程冠等[13]提出一种基于关联规则的社交网络好友推荐算法,其将新浪微博中用户之间的“关注”作为交易记录,将关注的用户作为交易项,所有交易项的集合作为交易数据库,生成二阶候选集,并按支持数降序排序,推荐出排名较高的用户作为好友。
综上所述,现有好友推荐算法通常基于用户显性的社交信息和社会关系,结合数据挖掘技术、统计学方法等进行好友推荐。但这类显性信息多包含结构化与非结构化数据,如短文本、链接、视频、音频、图片等,需要经过复杂的数据处理技术转换成能够描述用户特征的结构化数据才能有效利用[14-16]。同时,这些显式信息的准确获取比较困难,信息中存在信息不完整以及虚假成分等问题,以此信息提取的用户特征向量往往是不准确的。相对于用户显性信息,用户的隐性社会关系往往能为好友推荐提供更多的有效因素。在社交网站的用户关系中,除强关系外,还存在弱关系[4-5]。弱关系是指二级人脉,实质是一种传递关注关系。例如,Simmel三元闭包理论中认为,在一个社交圈内,若两个人有一个共同朋友,则这两个人成为朋友的可能性会提高[18-19];Naruchitparames等[20]提出的FOF理论(好友的好友理论)认为,如果两个用户有很多共同好友,那么这两个用户很可能是好友。在社交网站中,弱关系往往具有较大的人脉关系价值,并能提供较为客观和可靠的数据,可以直接反映用户之间的隐含关联,并能更为准确地反映用户之间的相似性,为好友推荐提供支持[7, 17]。
本文以用户的隐性社会关系为研究对象,着重挖掘用户之间隐含的关联关系,提出一种新的好友推荐算法。该算法将用户选择好友的过程模拟为一个马尔科夫过程,为用户下一步选择关注的用户与当前关注的用户建立关联关系。同时基于此关联关系构造用户间网络有向图,以关联规则的置信度作为图中有向边的权重,并根据此加权有向图建立转移矩阵。结合PageRank 算法计算用户在社交关系中的实际权重,再将权重较高的用户作为潜在好友进行推荐。为便于描述,将该算法称为PeopleRank算法。基于该算法,引入用户影响力,本文又提出了基于用户影响力的PeopleRank算法。本文给出了两种算法的详细过程,并用实验分析说明了所提出算法的合理性和优越性。
2 理论基础
本文所提出的好友推荐算法是基于关联规则和PageRank算法的;因此,本节首先简要介绍这两种方法的基本原理。
2.1 关联规则
关联规则是一种数据刻画方式,主要是从数据中抽取频繁项集[21-23]。设I是一个项集,I={i1,i2,…,in},元素i1,i2,…,in称之为项。事务数据库D={T1,T2,…,Ti,…,Tm}是事务数据集的集合,Ti⊆I。关联规则的形式为X→Y,其中X⊂I、Y⊂I且X∩Y=∅。该关联规则的意义是,如果X中所有项都出现在某事务数据集,那么Y也有可能出现在该事务数据集。
关联规则通常用支持度和置信度衡量。规则X→Y的支持度是指事务数据库中包含X和Y的事务数与所有事务数之比,记为Support(X→Y),即:
(1)
规则X→Y的置信度是指事务数据库中包含X和Y的事务数与包含X的事务数之比。换言之,该规则的置信度等于所有包含X的事务中同时包含Y的事务的比例,记为Confidence(X→Y),即:
(2)
实际上,规则X→Y的支持度可以看作是X∪Y同时出现在事务中的概率P(X∪Y),即Support(X→Y)=P(X∪Y);规则X→Y的置信度可以看作是一个条件概率P(Y|X),即Confidence(X→Y)=P(Y|X)。关联规则挖掘就是在给定的事务数据库中找到那些支持度和置信度不低于给定阈值的关联规则。
2.2 PageRank算法
PageRank算法最早是在谷歌搜索引擎中对网页重要性进行排序的算法[24-26]。该算法将网页之间的链接关系表示成一个有向图,图中的节点代表网页,有向边代表网页之间的链接关系,并对图中的每个网页进行赋值(PageRank值)。对于一个网页而言,其PageRank值是来源于所有链向它的网页,而它也会将自己的PageRank值平均分配给所有它链向的网页。显然,网页被链接的次数越多,其PageRank值也就越高。
PageRank算法模拟了一个人浏览网页的行为,假设一个人从一个随机网页出发,除了可以点击当前网页的出链前进,还能够随机跳转到任一随机网页。
根据上述原理,网页PageRank值的计算公式定义如下:
(3)
其中,PR(Vi)是网页Vi的PageRank值;n是网页总数;d是阻尼系数,它表示一个人在浏览网页时,以d的概率点击当前网页上的出链进行浏览,以1-d的概率随机选择别的网页浏览;In(Vi)是所有链向Vi的网页集合;Out(Vj)是Vj链向的网页的集合;|Out(Vj)|是Vj出链的总数,即出度。
定义一个转移矩阵来表示有向图。假设网页节点数为n,则该矩阵M=(mij)n×n是一个n行n列的矩阵。如果节点i有k条出链,那么对每一个出边链向的节点j,矩阵第i行第j列的矩阵元素mij值为1/k;而其余节点的值为0。因此,可将公式(3)表示成如下形式:
(4)
PageRank算法就是通过计算网页的PageRank值对网页进行排序的,仅仅依赖于网页之间的链接关系,其计算可以离线完成。
3 基于用户社会关系的好友推荐算法
本节基于社会网络中用户间隐性关系,首先提出一种基于用户社会关系的好友推荐算法;然后,引入用户影响力,并提出综合考虑用户社会关系及用户社会影响力的好友推荐算法。
3.1 算法过程描述
本文提出的好友推荐算法将用户随机选择好友的过程模拟成一个马尔科夫过程[27],即在很大程度上,目标用户选择关注的下一个用户与当前已关注的用户之间是关联的,具体定义为:
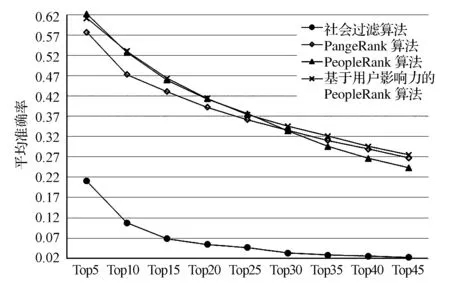
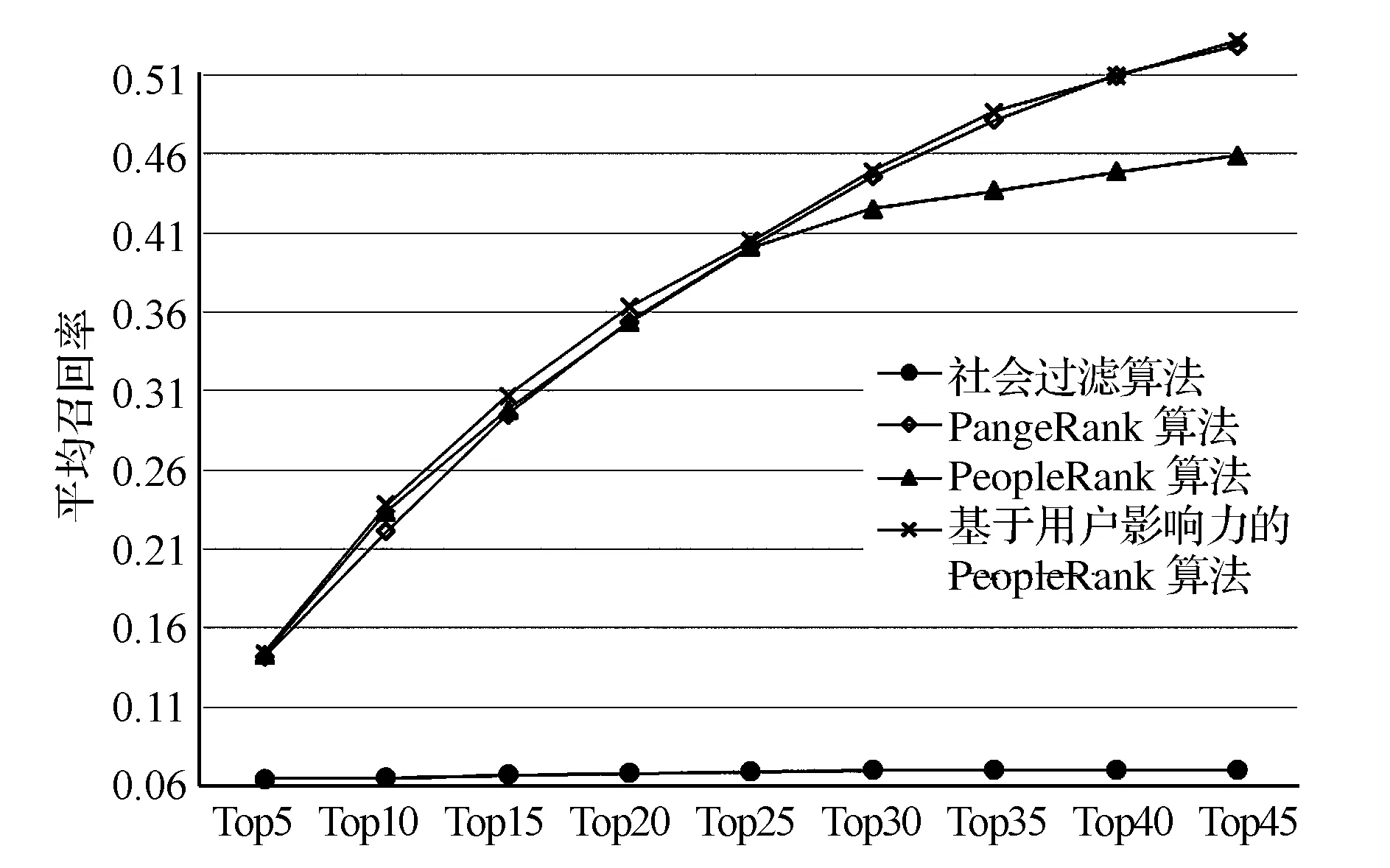
定义3.1:设目标用户为u,推荐候选集为U={u1,u2,…,un},对于任意m个非负整数t1,t2,…,tm(0≤t1 P{U(tm+k)=u′|U(t1)=u1,U(t2)=u2,…,U(tm)=um}=P(U(tm+k)=u′|U(tm)=um). (5) 其中,P(U(tm+k)=u′|U(tm)=um)是条件概率,亦为转移概率,表示在tm时刻目标用户选择关注了用户um的情况下,在tm+k时刻选择关注用户u′的概率。 在社交网站G=(U,E)中,U={u1,u2,…,un},令p(uj|ui)表示一步转移概率,其含义是:已知当前时刻目标用户u关注了ui,则下一步其选择关注用户uj的概率。因此,可定义如下转移概率矩阵: 定义3.2:一步转移矩阵可表示为P=(pij)n×n,其中,pij=p(uj|ui),具体形式如下: P= 其中,一步转移矩阵满足以下两个条件: (1)0≤p(uj|ui)≤1(i,j=1,2,…,n); 3.2 PeopleRank好友推荐算法 本文基于上述马尔科夫过程提出的PeopleRank好友推荐算法假设目标用户随机关注了一个用户,将会以一定的概率d选择与当前用户相关联的用户进行关注,并以(1-d)的概率随机选择别的用户进行关注。设目标用户u的推荐候选集U为包含了n个用户的集合,记为U={u1,u2,…,un}。具体算法过程描述如下: (1)利用关联规则构造用户之间的有向图 设ui,uj∈U,且j≠i,如果剩余n-2个用户中存在关注过ui的用户也同时关注了用户uj,称ui存在一条边指向uj,记为关联规则ui→uj;其表示关注过ui的用户也有可能关注uj。以此类推,当U中所有用户都建立了两两关联的有向边后,即可得到用户关系的有向图。 (2)计算有向边的权重 将关联规则ui→uj的置信度赋值于网络图中有向边的权重。记Confidence(ui→uj)是关联规则ui→uj的置信度,其表示关注过ui的用户也关注uj的概率。具体计算方法如下: 定义剩余n-2个用户中关注过ui的用户的数目为ui的支持度,记为Support(ui);剩余n-2个用户中同时关注过ui和uj的用户的数目为项集{ui,uj}的支持度,记为Support(ui,uj);则有: Confidence(ui→uj)= (6) (3)建立转移矩阵 设M是一个n×n矩阵,n为用户数量。于是,可得到关于目标用户u的转移矩阵M=(mij)n×n,(i,j=1,2,…,n),即: mij= (7) (4)计算候选集中用户的PeopleRank值 在得到转移矩阵M后,即可计算用户的PeopleRank值,即: 其中,PRu(ui)表示用户ui推荐给用户u的PeopleRank值,d是阻尼系数;mji是矩阵M的第j行第i列元素。根据式(8)可得到用户ui的PeopleRank值。 (5)Top-N用户推荐 根据得到的PeopleRank值,并将其按降序排列,并选取前N个用户(Top-N用户)推荐给目标用户。 上述PeopleRank好友推荐算法可总结为:通过用户之间的关联关系,构造有向图和转移矩阵;然后,计算用户的PeopleRank值,并进行排序,将PeopleRank值高的用户推荐给目标用户。从算法角度[18],该过程可描述为: 步骤1:构造用户之间的有向图,如果存在关注过ui的用户也关注了用户uj,就称ui存在一条有向边指向uj,否则不存在有向边。 步骤2:设矩阵M=(mij)n×n是n×n矩阵,n为用户数量,mij是关联规则ui→uj的置信度,它表示关注过ui的用户关注uj的概率。 步骤3:利用公式(8)计算用户的PeopleRank值。 步骤4:根据PeopleRank值输出值较高的Top-N用户列表。 3.3 综合考虑用户社会关系及社会影响力的PeopleRank好友推荐算法 PeopleRank好友推荐算法在进行PeopleRank值的计算时,将权重(1-d)平均分给了每个用户。因此,当目标用户不选择与当前用户相关联的用户,而以(1-d)的概率去随机关注其他用户,候选集中每个用户对于目标用户而言都是同等重要的。换言之,目标用户会以同等概率去选择关注其他用户。实际上,现实中人们往往会关注那些在社交网络中影响力较大的用户而不是其他普通用户。因此,我们提出一种假设:在这种情况下,目标用户可能更倾向于去关注那些比较有影响力的人。因此,考虑用户的影响力,基于用户影响力区分候选集中的用户修正所提出的PeopleRank好友推荐算法。 综合考虑用户社会关系及用户社会影响力的PeopleRank算法需要运用PageRank算法计算候选人集合中的每个用户的影响力,得到表示用户影响力的特定向量,记为eu=(e1,e2,…,en),其中ei表示目标用户u的候选集中用户ui的影响力。因此,基于式(8),可得到用户影响力的PeopleRank值,即: (9) 其中,PRu(ui)表示用户ui推荐给用户u的PeopleRank值;d是阻尼系数;mji是矩阵M的第j行第i列元素。 实验数据集来源于Arizona State University官方网站;该数据集收集了Twitter网站上一部分用户以及用户之间的社会关系[28]。本文选取了1658个用户,包含了60589个用户关系。用户关系数据集用Oracle数据库存储;实验硬件平台为Intel(R) Core(TM)i5-3230M CPU,主频为2.6GHz,4GB内存,500GB硬盘;操作系统为Windows 8.1;数据的查找和分离用Oracle语句完成,所有算法用C++语言实现。 实验采用交叉验证方法[17,29]开展;为此,将数据集分为80%的训练集和20%的测试集。对于目标用户u,将其已经关注的用户集合记为first-user(u),并将first-user(u)里面用户关注的用户记为second-user(u);将second-user(u)中的用户作为候选集,对目标用户u进行Top-N好友推荐。为说明本文所提出方法的合理性和有效性,将之与社会过滤算法和PageRank算法进行对比分析,并采用准确率和召回率进行评价分析[4,9]。其定义为: 准确率=推荐出的已经成为好友的用户数/推荐出的好友数; 召回率=推荐出的已经成为好友的用户数/好友总个数。 实验将使用好友推荐个数N=5,10,15,20,25,30,35,40,45等九种情况分别计算每种算法的准确率和召回率。为比较四种算法的有效性,根据每个算法的推荐结果,分别计算测试集中每个用户在每种情况(N值)下的好友推荐准确率和召回率;然后,计算测试集中所有用户在每种情况下的平均准确率和平均召回率。计算结果如图1和图2所示。 图1 不同N值情形下四种算法平均准确率对比 图2 不同N值情形下四种算法平均召回率对比 图1显示了不同N值情况下四种好友推荐算法的平均准确率。结果显示:社会过滤算法在每一个N值下的平均准确率都远远低于其它3个算法;当N≤25时,PeopleRank算法的平均准确率明显高于PageRank算法的平均准确率;而当N>25时,其平均准确率要比PageRank算法平均准确率差。在每一个N值情形下,基于用户社会关系及用户影响力的PeopleRank算法的平均准确率都高于PageRank算法的平均准确率。就本文所提出的两种算法而言,当N≤25时,两种算法的平均准确率差异较小;而当N>25时,综合考虑用户社会关系及用户影响力的PeopleRank算法的平均准确率明显要高于PeopleRank算法的评价准确率。根据上述结果可知,社会过滤算法推荐的用户往往不被目标用户接受。当N较小时,基于用户社会关系的推荐算法的准确率高于PageRank算法,表明其推荐出来的用户更能让目标用户接受;但是随着N的增大,其推荐准确率就低于PageRank算法,即基于用户社会关系的算法更加适用于精准推荐而非大规模推荐。而综合考虑用户社会关系及用户影响力的推荐算法,在各种情况下,推荐出来的用户都更能让目标用户接受,即对于精准推荐和大规模推荐都具有明显优势。 图2显示了不同N值情形下四种好友推荐算法的平均召回率。与其它三种算法相比,社会过滤算法在每一个N值下的平均召回率都远远低于其它三个算法的平均召回率;综合考虑用户社会关系及社会影响力的PeopleRank算法在每一个N值情形下的平均召回率都优于PageRank算法及PeopleRank算法的平均召回率。当N≤15时,PeopleRank算法的平均召回率高于PageRank算法的平均召回率;而当N>15时,其平均召回率却差于PageRank算法的平均召回率。可见,社会过滤算法在用于好友推荐时,不能有效推荐目标用户真正感兴趣的用户。当N较小时,基于用户社会关系的推荐算法的召回率高于PageRank算法,表明其能挑选出更多的目标用户感兴趣的用户;但是随着N的增大,其推荐召回率低于PageRank算法,表明基于用户社会关系的推荐算法在大规模推荐时,推荐质量降低。而综合考虑用户社会关系及用户影响力的推荐算法,对于精准推荐和大规模推荐都具有明显优势。 基于上述实验结果,可得出以下结论: (1)社会过滤算法在用于Twitter这种双向关注型社交网络的好友推荐时,效果不理想,不适用于弱关系推荐; (2)PageRank算法仅仅考虑了用户的影响力而忽略了用户之间的关联关系,其推荐的好友大多是粉丝数较多的名人明星,而用户关注的名人明星通常是有限的,该算法具有一定的局限性; (3)当推荐人数N较少时,PeopleRank算法的推荐准确率明显高于PageRank算法,在社交网站中进行精准推荐时,可能会有更好的推荐效果;但是PeopleRank算法注重用户之间的关联关系,将随机选择集中的用户同等看待,可能会忽略那些更容易被大众熟知且影响力较高的用户,推荐效果具有局限性; (4)综合考虑用户社会关系及用户影响力的PeopleRank算法兼顾了用户之间的关联关系以及用户影响力,其推荐准确率和召回率是四种算法中最高的,能够更好地向目标用户推荐好友。 在线社交网站中存在海量用户,如何从中寻找出目标用户真正认识或感兴趣的潜在好友是社交网络相关研究的重要主题。在此背景下,本文提出了基于用户社会关系的好友推荐算法,其基本思想是将用户选择好友的过程模拟成一个马尔科夫过程,通过建立并挖掘用户间潜在的关联关系确定推荐好友集合。对于目标用户,选定其二级好友作为候选集;首先,通过关联规则去挖掘候选集中用户间的关联关系,以此重新构造用户间的网络有向图,并以关联规则的置信度作为图中有向边的权重;然后,根据加权有向图建立转移矩阵;最后,结合PageRank算法计算候选集中每个用户的分数,并将排名靠前的用户推荐给目标用户。基于此推荐算法,本文又引入了用户在社会网络中的影响力,对推荐算法进行修正,提出综合考虑用户社会关系及用户社会影响力的好友推荐算法。 为了验证本文所提出的两种算法的有效性,基于准确率和召回率两种评价指标,将其与社会过滤算法以及PageRank算法进行比较。为此,选取了Twitter网站上的数据进行实验分析。实验结果表明:当推荐人数较少时,本文提出的PeopleRank算法的推荐准确率和召回率是优于社会过滤算法和PageRank算法的,更适用于精准推荐;同时,本文提出的综合考虑用户社会关系及用户影响力的PeopleRank算法无论是在准确率还是召回率上都相对较高,表明其无论是用于精准推荐还是大规模推荐,都比另外三种算法具有更好的推荐效果。 本文所提出的算法采用Twitter网站上的数据,且数据集相对较小,未来的研究工作可以考虑采用FaceBook和新浪微博的数据,并尽可能扩大数据集,以进一步验证算法的有效性。此外,本文所提出的算法需要大量的迭代计算,算法有待完善。 [1] 中国互联网信息中心.2014年中国社交类应用用户行为研究报告[EB/OL].[2014-08-22].http://www.cnnic.net.cn/hlwfzyj/hlwxzbg/201408/P020140822379356612744.pdf. [2] Shriver SK,Nair HS,Hofstetter R.Social ties and user-generated content: Evidence from an online social network[J].Management Science,2013,59(6):1425-1443. [3] Zheng Yu, Zhang Lizhu, Ma Zhengnin, et al.Recommending friends and locations based on individual location history [J].ACM Transactions on the Web (TWEB),2011,5(1):5. [4] 胡文江,胡大伟,高永兵,等.基于关联规则与标签的好友推荐算法[J].计算机工程与科学,2013,35(2):109-113. [5] 于海群,刘万军,邱云飞.基于用户话题偏好的社会网络二级人脉推荐[J].计算机应用,2012,32(05):1366-1370. [6] Weng Jianshu, Lim E P, Jiang Jing, et al. Twitterrank: Finding topic-sensitive influential twitterers[C]//Proceedings of the third ACM international conference on Web search and data mining:New York, USA, February 04-06,2010. [7] Chen Jilin, Geyer W, Dugan C, et al. Make new friends, but keep the old: Recommending people on social networking sites[C]//Proceedings of the SIGCHI Conference on Human Factors in Computing Systems. Boston, USA, April 04-09,2009. [8] Huang Wuhan, Meng Xiangwu, Wang Licai. A collaborative filtering algorithm based on users' social relationship mining in mobile communication network [J].Journal of Electronics and Information Technology,2011,33(12):3002-3007. [9] 高永兵,杨红磊,刘春祥,等.基于内容与社会过滤的好友推荐算法研究[J].微型机与应用,2013,32(14):75-78. [10] 舒琰,向阳,张骐,等.基于PageRank的微博排名MapReduce算法研究[J].计算机技术与发展,2013,23(2):73-76. [11] 王平,龙毅宏,唐志红,等.基于社会关系的互联网信任建立模式研究[J].软件,2011,32(4):12-15. [12] Chen Can, Feng Haodi. Microblog recommendation based on user interaction[C]//Proceedings of 2012 2nd International Conference on.Computer Science and Network Technology (ICCSNT),December 29-31,2012. [13] 向程冠,熊世桓,王东.基于关联规则的社交网络好友推荐算法[J].中国科技论文,2014,9(1):87-91. [14] 丁兆云,贾焰,周斌.微博数据挖掘研究综述[J].计算机研究与发展,2015,51(4):691-706. [15] 官思发,朝乐门.大数据时代信息分析的关键问题、挑战与对策[J].图书情报工作,2015,59(3):12-18. [16] 赵宇,黄思明,陈锐.数据分类中的特征选择算法研究[J].中国管理科学,2013,21(6):38-46. [17] 徐志明,李栋,刘挺,等.微博用户的相似性度量及其应用[J].计算机学报,2014,37(1):207-218. [18] Klimek P, Thurner S. Triadic closure dynamics drives scaling laws in social multiplex networks [J].New Journal of Physics,2013,15(6):63008-63016. [19] Opsahl T. Triadic closure in two-mode networks: Redefining the global and local clustering coefficients [J].Social Networks,2013,35(2):159-167. [20] Naruchitparames J, Gunes M H, Louis S J. Friend recommendations in social networks using genetic algorithms and network topology[C]//Proceedings of 2011 IEEE Congress on.Evolutionary Computation (CEC).New Drleans, USA, June 5-8,2011. [21] Orriols-Puig A, Martínez-López F J, Casillas J, et al. Unsupervised KDD to creatively support managers' decision making with fuzzy association rules: A distribution channel application[J].Industrial Marketing Management,2013,42(4):532-543. [22] 张玲玲,周全亮,唐广文,等.基于领域知识和聚类的关联规则深层知识发现研究[J].中国管理科学, 2015,23(2):154-161. [23] 蔡伟杰,张晓辉.关联规则挖掘综述[J].计算机工程,2001,27(5):31-33. [24] 欧卫,欧缤忆,谢赞福,等.一种基于PageRank的微博用户影响度评估算法[J].计算机与现代化,2013,(12):34-37. [25] Rajaraman A, Ullman J D.大数据:互联网大规模数据挖掘与分布式处理[M].王斌,译.北京:人民邮电大学出版社,2012. [26] 李强,王申康.一种基于PageRank算法原理的会员人气度排序算法[J].计算机系统应用,2008,(1):27-30. [27] 姬新龙,周孝华.基于马尔科夫随机波动和极值理论的风险测度[J].中国管理科学,2014,22(10):44-51. [28] Arizona State University. Twitter dataset[R/OL]. http://socialcomputing.asu.edu/datasets/Twitte. [29] Hsu W H, King A L, Paradesi M S R, et al. Collaborative and structural recommendation of friends using weblog-based social network analysis[C]//Proceedings of AAAI Spring Symposium:Computational Approaches to Analyzing Weblogs.Stanford, California, USA, March 27-29,2006. Friend Recommendation Algorithm based on User Relations in Social Networks JING Nan1,WANG Jian-xia1,XU Hao2, BIAN Yi-wen1 (1.SHU-UTS SILC Business School, Shanghai University, Shanghai 201899, China; 2. Schoolof Business, Anhui University, Hefei 230601, China) Due to the vast amounts of users, it is difficult for a user to make effective connections with others for common interests. Friend recommendationon online social networks, therefore, becomes a challenging research issue, which may have significant effects on sustainable developments of social networks.Most of the existing friend recommendation methods are conducted based on users’ explicit informationsuch as background, demography, interests and posts, while ignoring users’ implicit informationsuch as their social relationships. Notably, explicit information is often incomplete and not trustworthy, and cannot be appropriately used to measure user similarities.In order toeffectively recommend friends, a recommendation algorithm is proposed based on user relationship information in online social networks. In the described algorithm, user relationships are characterized by using the association analysis method, and then a weighted, directed graph between network users is constructed. Based on this graph, this algorithm builds a transition matrix and uses the PageRank algorithm to calculateusers’ scores that indicate the acceptance probabilities, and then recommend the users with high scores to the target user on social networks. In addition, with the consideration of the user authority in a specific social network, an enhanced friend recommendation algorithm is further developed.In order to validate the proposed approaches, friend recommendation experiments on Twitter are conducted and the users’ information and their relationship data are extracted. For this purpose, two traditional methods, i.e., social filtering algorithm and the PageRank algorithm, are used to compare with the two proposed approaches based on two measures, i.e., accuracy and recall rate. Experiments results show that the proposed recommendation algorithms yield clearly better results in accuracy and recall rate than the traditional recommendation algorithms. social networks; friend recommendation; social relationship; user authority; PageRank algorithm 1003-207(2017)03-0164-08 10.16381/j.cnki.issn1003-207x.2017.03.019 2015-11-18; 2016-05-14 国家自然科学基金面上资助项目(71371010,71571115);上海市科学委员会科技人才计划项目(14PJ1403700);上海市教育委员会科研创新项目(14YS006);教育部在线教育研究中心在线教育研究基金(全通教育)项目资助(2016YB138) 卞亦文(1978-),男(汉族),安徽芜湖人,上海大学悉尼工商学院,博士,教授,研究方向:服务运作管理、决策分析,E-mail:ywbian@shu.edu.cn. C931;TP39 A4 实验分析
5 结语

