应急预案的执行状态优化问题研究

石 彪，薛旭旭，池 宏，祁明亮

(1.中国科学院科技政策与管理科学研究所，北京 100190；2.中国科学院大学工程科学学院,北京 100049)



应急预案的执行状态优化问题研究

石 彪1，薛旭旭2，池 宏1，祁明亮1

(1.中国科学院科技政策与管理科学研究所，北京 100190；2.中国科学院大学工程科学学院,北京 100049)

突发事件的发展演变具有极强的不确定性，随着时间的推进，突发事件对应急处置的需求会发生变化，而处于执行过程中的预案,尤其是其中的部分工序可能不再适用，及时地调整预案工序的执行状态对提升整体应急处置效率具有重要意义。针对突发事件应急处置中不确定的应急处置需求，结合应急处置与事件演化的动态博弈特征，从可操作性应急预案的执行工序层面对应急预案的执行状态优化问题进行了研究，解决了特定时刻预案工序的执行状态选择问题，为根据突发事件的实时信息调整可操作性应急预案工序的执行状态提供决策辅助。

突发事件；应急预案；执行状态优化

1 引言

应急预案是为了满足突发事件可能出现的应对需求而预先制定的处置方案，尤其是操作层面的预案，其具有明确的处置目标和适用条件[1-3]。目前, 我国各级政府已经制定了应对各类突发事件的应急预案体系[4]，但从应急预案的编制和使用情况来看，目前的大多数预案仍然是通过对特定类型突发事件的应对经验进行总结得出的应急处置工作流程，这为应急管理者提供了基本的决策支持,但突发事件的发展演变具有很强的不确定性，其既取决于事件演变的时间规律，也受前期应急处置效果的影响[5]。此外，在某些特定领域，尤其是生产领域的应急处置中，应急资源在一定时间窗口内的种类和数量也往往是有限的[6-7]。因此，面对实时变化的应急处置需求，处于执行过程中的整体预案或其中的部分处置动作可能不再适用，及时地调整其执行状态，选择关闭、暂停或重启这些处置动作，对促进有限应急资源的有效利用，提升预案的整体处置效率具有重要意义。

目前国内外针对应急预案的执行状态优化问题研究相对较少。瞿斌[8]等针对应急决策方案的动态调整问题,提出了一种基于调整成本、调整损失和处置效果三因素的期望效用最大化方法。姜艳萍[9]等考虑了应急处置效果和应对损失、不同方案之间的转换成本等因素下,给出了应急决策方案的动态调整方法。于辉[10]研究了在决策者完全没有突发事件持续时间信息的条件下，单个或两个企业何时启动应急预案的问题。张玲等[11]通过构建基于情景的最小最大后悔值准则鲁棒优化模型,研究了应急救灾网络构建方法。盛方正等[12]假设企业会采取措施收集有关突发事件的信息，并且会根据它掌握的信息，对突发事件的持续时间进行预测，然后对单个及多个企业何时启动应急预案进行了分析。余昇等[13-14]考虑了预案启动后损失立即停止和逐渐停止两种情形下的应急预案启动策略。于辉等[15]在启动应急预案之前加入了前期处置环节，研究了管理者面对突发事件时应该何时启动前期处置方案和应急预案的问题。王长峰[16]等研究了针对重大工程应急管理决策问题，构建了基于系统内部网络组织的动态博弈模型。周传贤[17]提出了关于商场启动应急疏散预案的时机，即通过判断商场是否达到最大人流密度来确定启动疏散预案时机，为商场在节假日人流高峰时启动预案提供了思路和方法。Cormack等[18]研究了基于设计结构矩阵(DSM)的软件模块化重构方法，田军等[19]进一步基于DSM研究了应急任务流程模块化的方法，为应急流程的动态重组提供了可行途径。

上述研究主要集中在应急预案的动态调整问题上，其选择预案启动与否的原则往往是以应对成本最小化为目标，将突发事件发展演变的不确定性归结为持续时间的不确定性，而这些都与应急管理的现实情况存在一定差距。应急预案的启动与否之所以存在选择问题正是因为突发事件的发展演变具有不确定性，这种不确定性不仅表现为已经发生的突发事件的持续时间不确定，更重要的是突发事件的发展演变方向本身存在极强的不确定性。预案的启动必然涉及成本投入，但启动预案的最终目标仍然是为了尽可能降低突发事件造成的损失。此外，从问题研究的对象来看，除了当突发事件存在多个可能的演变方向，而需要在多个备选预案中进行选择，从而涉及应该在何时、启动或关闭某些预案之外，预案中的具体处置动作也存在需要根据突发事件的实际演变情形采取适时启动、关闭或暂停执行的问题。本文将针对以上不足，围绕应急预案中具体处置动作的执行状态问题展开研究。

传统的应急预案是文本型的，为了更好地利用其中所包含的应急处置信息，便于计算机存储和运算，对应急预案的数字化表达非常必要。应急处置流程是应急预案的重要组成部分，其包含反映突发事件演变过程的关键场景点和一系列具有逻辑顺序的处置动作，是应急预案中的核心内容，也是应急预案数字化表达的基础[1]。为了尽可能保持预案中应急处置动作的逻辑序关系，本文将借鉴项目管理中对网络计划的表述方式，将应急预案表达为以应急处置流程为核心的网络计划图，图中的工序表示具体的应急处置动作，每个工序具备工期、完成结束时间和资源等属性。

预案工序的执行涉及具体资源的调用，根据处置动作和资源调用情况不同，将工序的执行状态分为启动、关闭和暂停三种(如表1所示)：

表1 应急预案中工序的三种执行状态

启动状态是指执行具有特定目标的处置动作，并使用一定数量的资源来完成这一处置动作；关闭状态是指停止执行某个处置动作，并释放其执行启动状态时需要占用的资源；暂停状态是指停止执行某个处置动作，但仍然占用启动状态下需要使用的资源。以飞机起落架故障应急处置为例，在地面准备的过程中需要将拖车开到指定位置待命，如果起落架故障未能排除，则可以使用拖车将受损飞机拖走；如果故障排除，尚未到位的拖车准备工作将调整为关闭(返回)或暂停(原地待命)状态。

2 问题描述

突发事件的发展演变具有极强的不确定性，随着时间的推进，突发事件对应急处置提出的需求信息不断更新，而应急预案中工序的执行状态也需要做出相应的调整，使得应急处置能够更快更好地满足突发事件的不确定需求。

突发事件自身造成的直接损失往往难以估量，但由于应急处置的不及时或低效所造成的间接损失也常常占到了相当重要的比重，尽可能降低由于应急处置不当造成的间接损失是提升应急管理水平的重要内容。

由于预案中工序的执行状态选择不当造成的间接损失有以下几类：

(1)资源准备不足造成的紧缺损失。应急处置需要的资源如果准备不足会直接影响应急处置的效果，其造成的损失往往是最为明显和直接的。

(2)资源准备过量造成的闲置损失。应急处置强调效率和时间，但并不代表在任何时刻都可以不计成本，在缺乏总体计划和实际处置需求信息的情况下做出的过量的资源调用不仅造成资源的闲置损失，还常常有损应急处置的效率。

(3)资源占用造成的机会损失。资源占用会造成一定的机会损失，如拖车原地待命会造成有限的资源在其他场合无法使用。

(4)执行状态切换造成的损失。工序的执行状态在不同状态之间进行切换时是有成本的，暂停状态是介于关闭和启动之间的一种中间状态，因为涉及资源的占用和释放，三种状态之间的切换以启动和关闭状态之间的切换成本最高。

预案中工序的执行状态优化问题是在已知时刻t突发事件的各种可能情景的发生概率、工序i的工期、资源参数和工序i在三种执行状态之间切换的损失参数，针对时刻t的工序i构建执行状态优化模型，通过选择工序i在t时刻的执行状态，尽可能降低由于资源不足或者闲置造成的期望损失、t-1时刻执行状态切换为t时刻状态的损失以及资源占用造成的损失，为预案执行过程中的实时决策辅助提供依据。

3 模型构建

3.1 符号定义

c：场景，是指处置主体要素、影响处置的周边环境要素和资源要素在某个时刻所处状态的取值集合；当突发事件性质发生变化、处置空间或对象发生改变、处置任务目标发生变动时的场景为关键场景。

s：情景，是指从突发事件的发生时刻开始，经过一个或多个关键场景的切换后到达结束时刻的一条可能的场景演变路径。

S：情景集合，s∈S；

Ia：应急准备阶段工序集合；

Ib：应急处置阶段工序集合；

Ic：应急善后阶段工序集合；

I：工序集合，i,j∈I={1,2,…n}，n代表所有工序中的末尾工序，I=Ia+Ib+Ic；

K：资源种类集合，k∈K={1,2,3,4}={人员、工具、设备、物资}；

t：突发事件演变过程中的某个时刻，t=1,2,…,n；

ηst：情景s在t时刻的发生概率；

rsik：情景s中工序i调用资源k的数量；

psi：情景s中工序i的工期；

准备阶段工序的工期主要取决于资源调集的时间。对于所需资源储备数量较少，需要多次调运的，其工期取决于需要调配资源的数量，如果存在多种资源需要调集时，其工期取决于关键资源的需求数量；对于所需资源储备数量充足，可以采取一次或并行调集的，其工期受资源量的影响不大。假设以上两种模式的工序具有如下关系：

psi=usi·rsik*+vsi,i∈Ia

usi: 表示准备单位关键资源k*所用的工期，usi≥0；

vsi：为准备阶段工序的工期常数；

处置和善后阶段的工序都是在既定资源准备基础上完成的工作。有些工序的工期主要取决于所用关键资源数量的大小，所能调用的资源越多，其工期越短。比如飞机起落架故障应急处置阶段的客货安置工序，地服人员越多，其安置所需时间越短；但也有部分工序的工期与所用资源量的多少无关，如残损航空器搬移工序，并非拖车越多越快，其处置时间基本不受拖车数量的影响。假设以上两种工序的工期有如下关系：

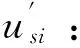
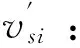
Νsik：情景s中第i个工序对资源k的需求数量；

Φk：单位资源k的临时调用成本(紧缺情况)；

Γk：单位资源k的闲置成本(过度应对情况)；

Ωk：单位资源k在暂停状态下，单位时间内被占用造成的机会损失；

αsit：0-1变量，如果情景s中工序i在时刻t启动则为1，否则为0；

βsit：0-1变量，如果情景s中工序i在时刻t关闭则为1，否则为0；

γsit：0-1变量，如果情景s中工序i在时刻t暂停则为1，否则为0；

αsi：表示情景s中工序i在时刻t之前执行启动状态的总时长；

βsi：表示情景s中工序i在时刻t之前执行关闭状态的总时长；

γsi：表示情景s中工序i在时刻t之前执行暂停状态的总时长；

m：工序i在t-1时刻的执行状态(m∈{αs,i,t-1,βs,i,t-1,γs,i,t-1})；

n：工序i在t时刻的执行状态(n∈{αsit,βsit,γsit})；

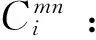
3.2 模型假设和约束

预案中工序的执行状态优化建模需要满足以下假设和条件：

(1)执行状态的唯一性约束。对任何一个时刻的某项工序而言，在启动、关闭和暂停三种执行状态中只能选择一种状态实际执行。即αsit+βsit+γsit=1。

(2)工期与资源量的函数为可逆函数。对应急准备阶段的工序而言，实际调运的资源量为：

类似的，对应急处置和善后阶段的工序而言，实际调运的资源量为：

(3)应急处置需求的不确定性包含两部分，一是当前场景对应急资源种类和数量的需求参数是不确定的，二是当前情景对应急处置动作的时间需求是不确定的。这需要实时更新工序的安排方案，即根据情景发生演变的实时信息更新工序的时间和资源调度方案，这属于在线动态生成应急处置方案的问题范畴[15-17]，这也是目前应急预案智能化研究领域的热点问题之一。

3.3 优化目标

应急预案中工序的执行状态选择需要依据实时更新的应急处置方案，考虑未来多个情景的发生概率，以及不同情景对资源和处置时间的需求变动，来确定应急资源使用效率最高的执行状态方案。由于处于不同阶段的工序具有不同类型的工期资源函数形式，接下来将分别讨论。

3.3.1 资源准备阶段工序

(1)当usi>0时，构建如下目标：

Min{EXa|i∈Ia,usi>0}=

式中[•]+表示当方括号中的值大于零时，该函数值为原始值，否则为0。

式中第一项表示启动状态时由资源准备不足造成的紧缺损失；第二项表示启动状态时由资源准备过量造成的闲置损失；第三项表示暂停状态对资源占用造成的机会损失；第四项表示不同执行状态之间的切换损失。

(2)当usi=0时，构建如下目标：

式中1{·}是一个指示性函数，即当大括号中的值大于零时，该函数值为1，否则为0。

式中第一项表示启动状态时由资源准备不足造成的紧缺损失；第二项表示启动状态时由资源准备过量造成的闲置损失；第三项表示暂停状态对资源占用造成的机会损失；第四项表示不同执行状态之间的切换损失。

3.3.2 应急处置和善后阶段的工序

类似资源准备阶段，有：

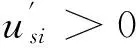
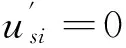
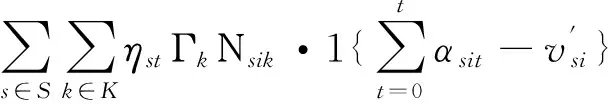
综上，对应急预案工序执行状态的优化模型可以归纳为：

(1)

s.t.αsit,βsit,γsit={0,1}

(2)

αsit+βsit+γsit=1

(3)

基于以上优化目标和约束构建的模型为0-1整数线性规划模型，在预案工序数量规模有限的情况下，采用Lingo或Cplex等整数线性规划软件包能够快速求得最优解，能够为实时选择工序执行方案中各个工序的最优执行状态提供决策支持。但当工序数量规模较大(超过1000)时，采用线性规划软件包计算结果也极为耗时，可以采用包括分支定界和排序等算法相对快速地求得最优解。考虑到应急管理实践的特点，应急预案时为了快速应对突发事件的处置方案，且应急预案一般都是采取分层编制的方法，其每层预案的工序数量一般不会超过100个，采用现有整数线性规划软件求解在应急状态下的预案工序执行状态最优解具备可行性。

4 算例

4.1 算例说明

(1)情景假设：航空公司在t=0时刻收到飞机发生空中颠簸信息，t=30时刻收到飞机发生起落架故障信息，在考虑工序的资源、时间约束条件下生成了工序安排方案后，随着应急处置工作的开展，情景参数发生变化，现需要根据事件进展调整工序在某一时刻的执行状态。

(2)工序初始安排方案：初始方案见图1,工序的工期和资源参数见表2，其中情景G表示收到突发事件初始信息，情景G1表示故障未排除情景，情景G2表示故障成功拍出情景。假设当前时刻为t=30，已经完工的工序包括工序1～10，正在进行的工序为“机务地面处置准备”，未开始的工序包括16～35。

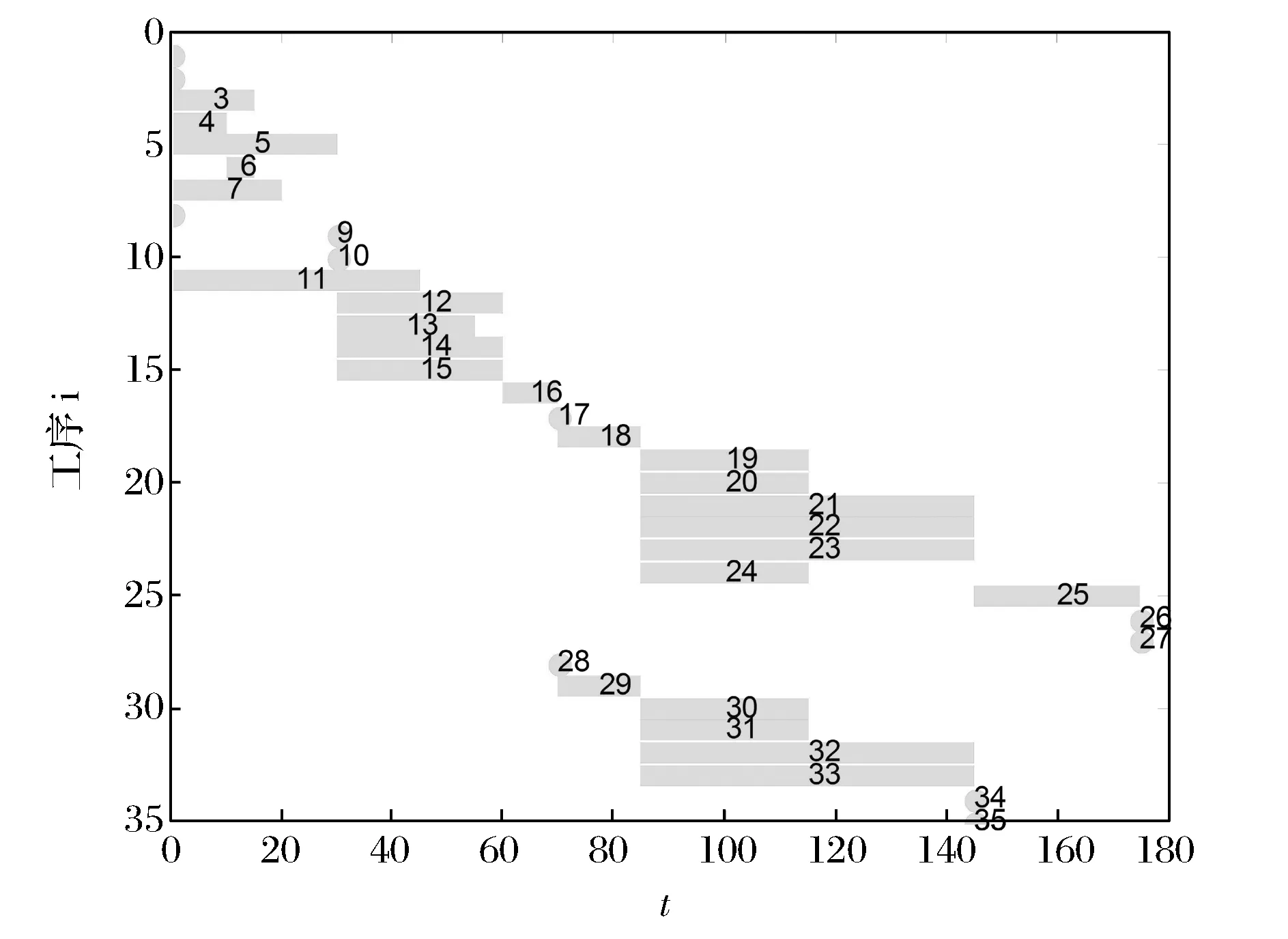
图1 预案初始工序安排方案

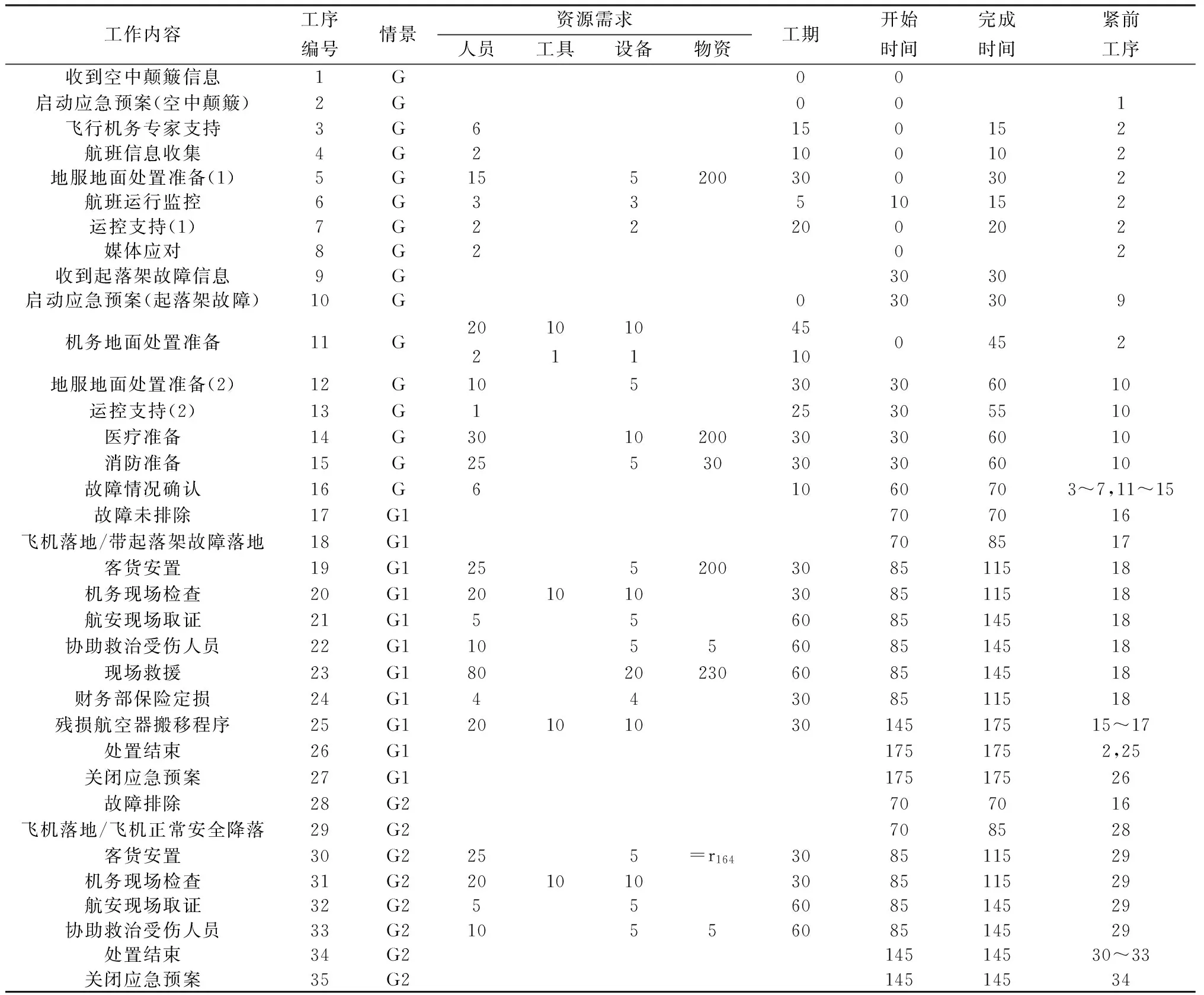
工作内容工序编号情景资源需求人员工具设备物资工期开始时间完成时间紧前工序收到空中颠簸信息1G00启动应急预案(空中颠簸)2G001飞行机务专家支持3G6150152航班信息收集4G2100102地服地面处置准备(1)5G155200300302航班运行监控6G33510152运控支持(1)7G22200202媒体应对8G202收到起落架故障信息9G3030启动应急预案(起落架故障)10G030309机务地面处置准备11G20210110145100452地服地面处置准备(2)12G10530306010运控支持(2)13G125305510医疗准备14G301020030306010消防准备15G2553030306010故障情况确认16G61060703～7,11～15故障未排除17G1707016飞机落地/带起落架故障落地18G1708517客货安置19G1255200308511518机务现场检查20G1201010308511518航安现场取证21G155608514518协助救治受伤人员22G11055608514518现场救援23G18020230608514518财务部保险定损24G144308511518残损航空器搬移程序25G12010103014517515～17处置结束26G11751752,25关闭应急预案27G117517526故障排除28G2707016飞机落地/飞机正常安全降落29G2708528客货安置30G2255=r164308511529机务现场检查31G2201010308511529航安现场取证32G255608514529协助救治受伤人员33G21055608514529处置结束34G214514530～33关闭应急预案35G214514534

(3)情景参数变化情况

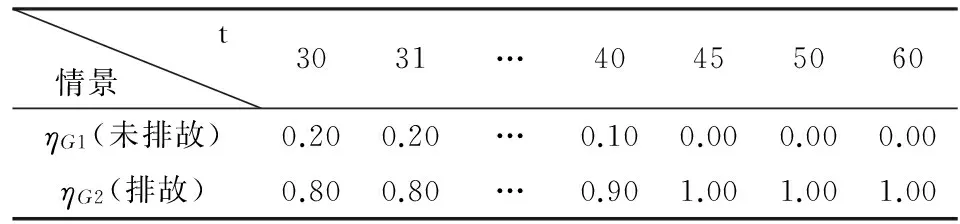
表3 各时刻的情景概率

(4)需求参数变化情况

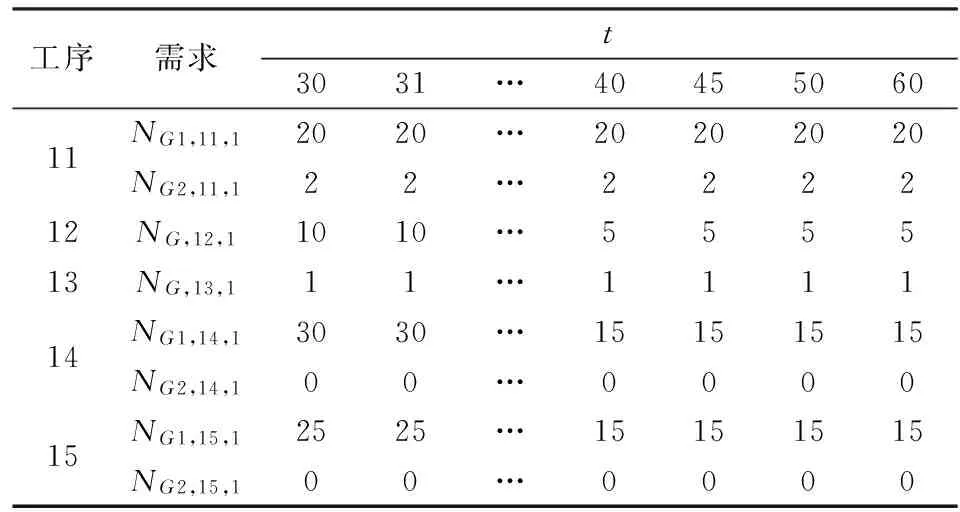
表4 各时刻的需求参数

(4)状态切换参数

表5 状态切换损失参数

4.2 模型计算

4.2.1 工序11在各时刻的启动状态优化模型

取初始参数如下：

us,11=0.56,vs,11=33.89,S={G1,G2},k*=1,Φ1=0.8,Γ1=0.2, Ω1=0.15

由于us,11>0，且工序11处于应急准备阶段，求解优化模型可得t=30～46各时刻目标值如表6所示：

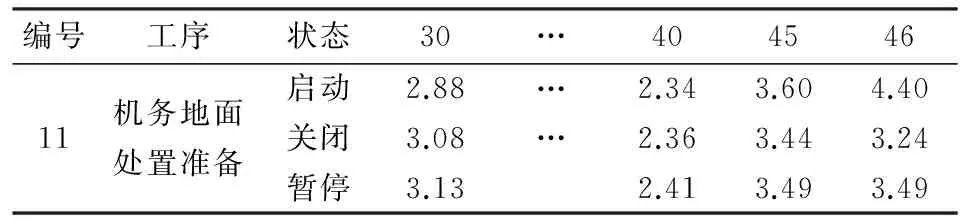
表6 工序11的执行状态优化结果

因此，工序11在t=30～44期间将选择启动状态；在t=45～60期间将选择关闭状态。

4.2.2 工序12到工序15在各时刻的启动状态优化模型

由于工序i=12～15的usi=0，且属于应急准备阶段，求解优化模型可得t=30～61各时刻的目标值如表7～10所示：

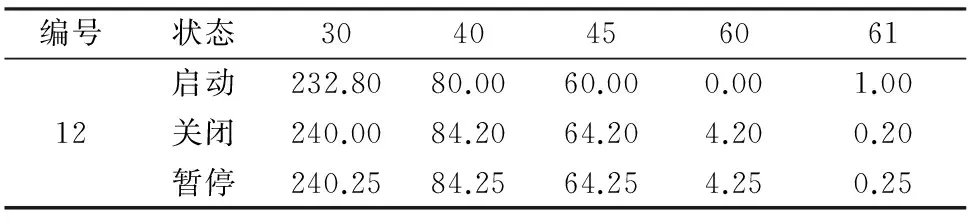
表7 工序12的执行状态优化结果

工序12在t=30～60期间将选择启动状态，在t=61之后选择关闭状态。

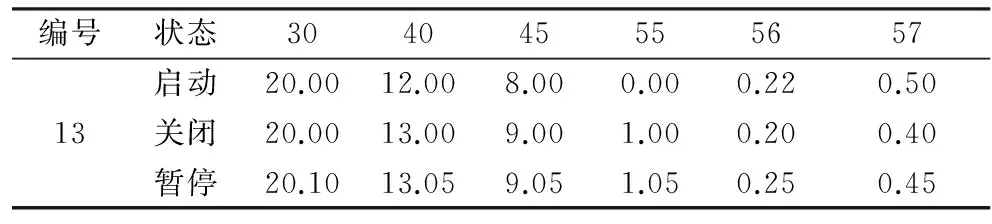
表8 工序13的执行状态优化结果

工序13在t=30～55期间将选择启动状态，在t=56之后选择关闭状态。

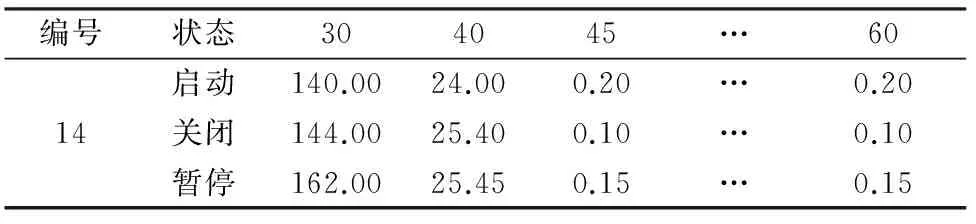
表9 工序14的执行状态优化结果

工序14在t=30～44期间将选择启动状态，在t=45之后选择关闭状态。

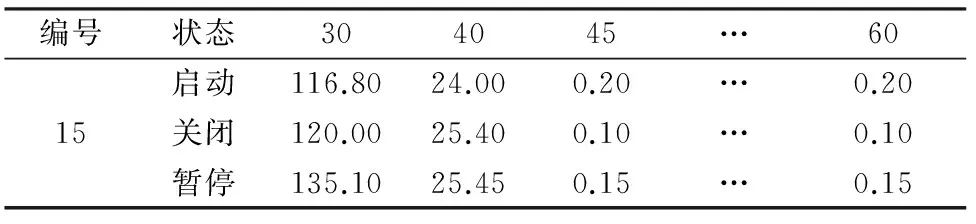
表10 工序15的执行状态优化结果

工序15在t=30～44期间将选择启动状态，在t=45之后选择关闭状态。

4.3 结果分析

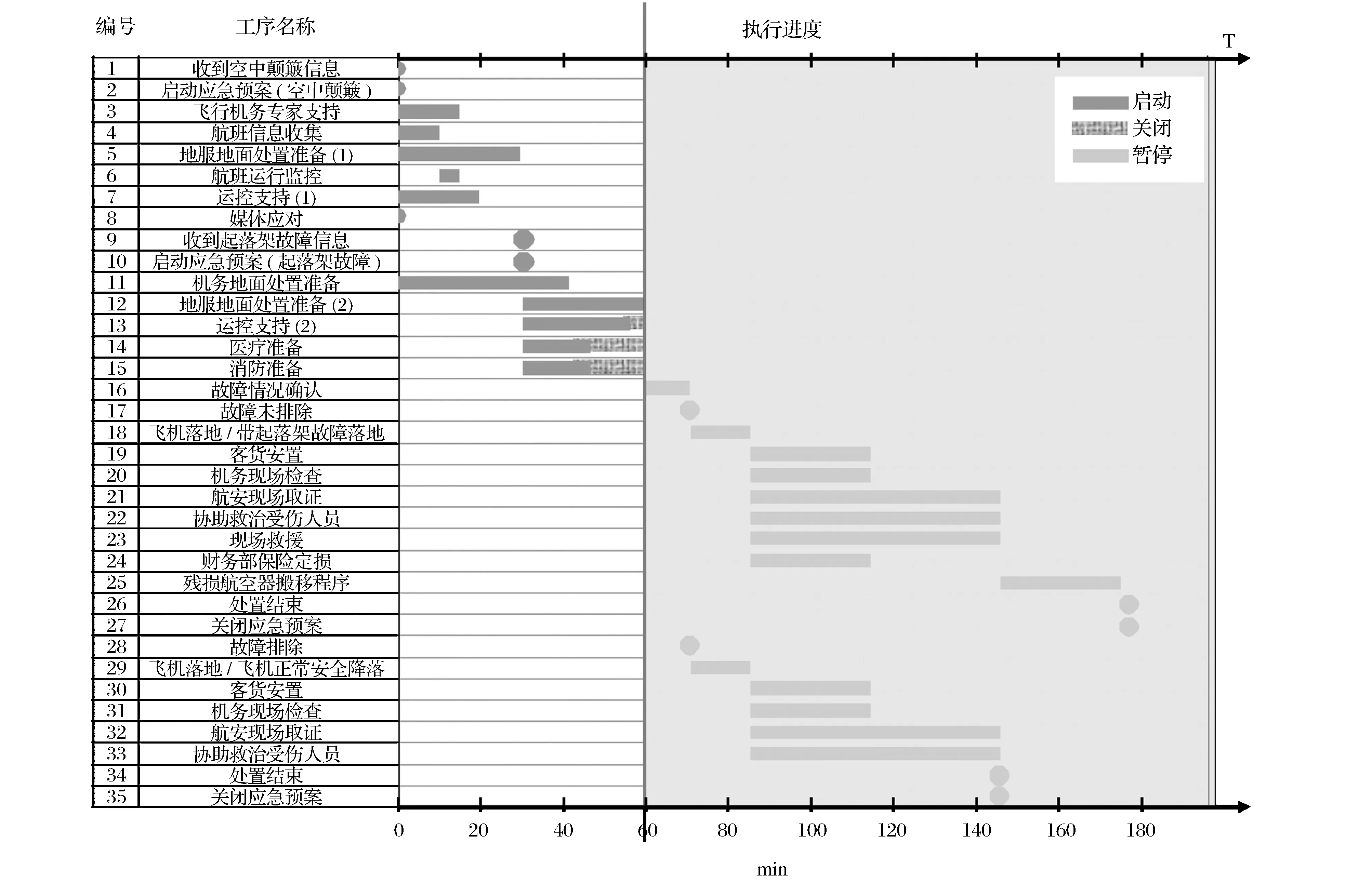
图2 预案的执行状态优化结果

综合上述算例结果，当预案执行至t=60时，其执行过程的信息如图2所示。从结果中可以看出，情景发生概率和需求参数的变化都对工序的执行状态产生了影响。当t=40时，两种可能情景的发生概率发生了明显变化，排故成功的预期得到进一步增强，这时排故不成功的可能性仍然存在，由于预先设置的物资紧缺损失的惩罚值较大，在t=40～45期间，所有工序的紧缺期望损失仍然较高，大部分工序仍然按照原计划执行启动状态，这与实际应急处置过程中“杜绝侥幸，全力以赴”的处置理念是一致的；当t=45时，两种可能情景的发生概率再次发生变化，排故成功已成定局，此时，机务、医疗和消防准备都选择了关闭状态，因为继续执行启动会造成更大的资源闲置损失。相对而言，工序12和工序13的处置工作并不受不同情景的影响(两种情景下的需求参数相同)，都会执行启动状态到原计划工期结束为止。

5 结语

应急预案是为了满足突发事件特定情景需求下的应急处置方案，当初始情景发生触发预案启动后，随着突发事件的演化，这时需要调整部分工序的执行状态来提升应急资源的使用效率。本文在预案的网络计划表达和工序初始安排方案构造的基础上，定义了工序的三种执行状态，并分析了由执行状态选择不当造成的间接损失，包括资源准备不足造成的紧缺损失、资源准备过量造成的闲置损失、资源占用造成的机会损失、执行状态切换造成的损失等，依据损失最小原则建立了应急预案的执行状态优化问题的数学模型，最后通过实例分析讨论了不同情景下工序状态的选择优化过程。本文的方法解决了可操作性预案在特定时刻工序的执行状态选择问题，能够为根据突发事件的实时信息调整应急预案工序的执行状态提供决策辅助。

[1] 于瑛英,池宏. 基于网络计划的应急预案的可操作性研究[J]. 公共管理学报, 2007, 4(2): 100-107.

[2] Qi Mingliang, Chi Hong, Ji Lei, et al. A study on the method for constituting an operable emergency plan[C]//Proceedings of the 3rd International Conference on Management and Service Science，Beijing, China,2009.

[3] 石彪,祁明亮，邵雪琰，等.乌鲁木齐社区应急管理机制路线图[J]. 国家行政学院学报，2012,(2):35-40.

[4] 吴宗之, 刘茂. 重大事故应急预案分级、分类体系及其基本内容 [J]. 中国安全科学学报, 2003, 13(01): 18-21.

[5] Cohen R, Weinisch K. The impact of a major earthquake on the evacuation of the emergency planning zone of a nuclear power plant [J]. Journal of emergency management, 2015, 13(2): 135-43.

[6] Liang Yan, Bao Jinsong, Hu Xiaofeng, et al. A heuristic project scheduling approach for quick response to maritime disaster rescue[J]. International Journal of Project Management 2009,27(6): 620-628.

[7] 胡信布, 何正文, 徐渝. 基于资源约束的突发事件应急救援鲁棒性调度优化 [J]. 运筹与管理, 2013, 22(02): 72-9.

[8] 瞿斌，王雪芳. 基于效用的应急决策方案动态调整方法 [J]，统计与决策，2014，(7): 46-49.

[9] 姜艳萍，樊治平，苏明明. 应急决策方案的动态调整方法研究[J]，中国管理科学，2011，19(5): 104-108.

[10] 于辉，陈剑. 突发事件下何时启动应急预案[J]. 系统工程理论与实践, 2007,(8):27-32.

[11] 张玲，陈涛，黄钧. 基于最小最大后悔值的应急救灾网络构建鲁棒优化模型与算法[J]，中国管理科学，2014,22(7): 131-139.

[12] 盛方正，季建华，周娜. 基于供应链管理的应急预案启动时间研究[J]. 工业工程与管理，2008,(6):1-5.

[13] 余昇，徐寅峰，董玉成，等. 基于在线方法的蓝藻危机应急预案启动策略[J]. 系统工程理论与实践，2011,31(5):914-919.

[14] 余昇, 徐寅峰, 郑斐峰. 太湖水华危机应急预案在线风险补偿启动策略 [J]. 运筹与管理, 2011, 20(2): 117-24.

[15] 于辉，江智慧. 突发事件下分阶段启动应急预案模型研究[J]. 管理工程学报, 2011,25(1): 109-114.

[16] 王长峰，满颖. 基于动态博弈理论的重大工程应急管理决策研究[J]，中国管理科学，2013，(11): 173-179.

[17] 周传贤,杨阳. 商场启动疏散预案的最大人流密度思考[J]. 中国安全生产科学技术, 2007,3(5):122-125.

[18] Cormack A M, Rusnak J, Baldwin C Y. Exploring the structure of complex software design: An empirical study of open source and proprietary Code [J].Management Science,2006,52 (7):1015-1030.

[19] 田军，李莉芳，白剑，等. 基于DSM的应急任务流程模块化设计研究[J]，中国管理科学，2014，22(8)： 100-107.

Research on Executing State Optimization of Emergency Plan

SHI Biao1, XUE Xu-xu2, CHI Hong1, QI Ming-liang1

(1. Institute of Policy and Management, Chinese Academy of Sciences, Beijing 100190,China;2.School of Engineering Science, University of Chinese Academy of Sciences, Beijing 100190, China)

The development of emergency has a strong uncertainty, the demand of emergency treatment will change as emergency plan executing,so the overall plan or part of the processes may not be applicable for the changed demand, it will be significant to change the executing state of those processes for improving emergency response efficiency. In order to respond to uncertaintyemergency needs, consideringdynamic game features between the evolution of emergenciesand emergency response, the optimization problem of executing state has been studied in operational level, which can help selecting executing state in a specific moment as the emergency needs changed, and providingdecision support based on real-time information to adjust for emergency contingency plans and the implementation of the process state.

emergency event; emergency plan; executing state optimization

1003-207(2017)03-0156-08

10.16381/j.cnki.issn1003-207x.2017.03.018

2015-07-30；

2016-08-31

薛旭旭(1992-)，男(汉族)，河南南阳人，中国科学院大学工程科学学院，硕士，研究方向：应急管理，E-mail:xue_xuxu@126.com.

C931.1

A