包含广义Fibonacci多项式的循环矩阵行列式的计算

师白娟

(西北大学 数学学院, 陕西 西安 710127)

包含广义Fibonacci多项式的循环矩阵行列式的计算

师白娟

(西北大学 数学学院, 陕西 西安 710127)

主要研究包含广义Fibonacci、Lucas多项式的行斜首加尾右循环矩阵和行斜尾加首左循环矩阵的行列式,利用多项式因式分解的逆变换给出行斜首加尾右循环矩阵和行斜尾加首左循环矩阵,包含广义Fibonacci、Lucas多项式行列式的显式表达式.

行斜首加尾右循环矩阵; 行斜尾加首左循环矩阵; 广义Fibonacci多项式; 广义Lucas多项式; 行列式

0 引言

循环矩阵是一类非常重要的特殊矩阵,在现代科技工程领域应用广泛,比如分子震动、图像处理、通信、信号处理、编码、预处理等领域.文献[1]为其研究奠定了深厚的基础.近几年内循环矩阵的探究已经延伸到很多方面,成为活跃的研究课题,广泛应用于应用数学与计算数学的许多领域,如控制理论、最优化、求解(偏)微分方程、矩阵分解多目标决策、二次型化简及平面几何学,特别是在广义循环码方面[1-12].

循环矩阵类有许多特殊而良好的性质与结构,(右)循环矩阵、左循环矩阵、r循环矩阵、g-循环矩阵、Hessenberg矩阵、三对角矩阵、斜循环矩阵及一些特殊的f(x)-循环矩阵、行首加r尾r右循环矩阵(RFPrLrR)和行斜首加尾右循环矩阵,主要研究这些特殊矩阵的特征值、行列式、逆矩阵及范数,尤其是谱范数.文献[13]研究广义Fibonacci数列的循环矩阵的行列式;文献[14]给出Fibonacci-Lucas的一类循环矩阵的行列式;文献[15]给出包含Fibonacci数列的循环与斜循环矩阵的行列式;文献[16]讨论了包含Fibonacci数列和Lucas数列的循环矩阵的行列式;文献[17]给出包含Fibonacci和Lucas数列的Toeplitz矩阵的范数.xn-x+1-循环矩阵被称为RSFPLR循环矩阵,即行斜首加尾循环矩阵,比一般的f(x)-循环矩阵有更好的结构和性质,所以求解RSFPLR循环线性系统有更好的快速算法.

行斜首加尾循环矩阵不同于一般的循环矩阵,也不是行首加r尾r右循环的特殊形式,而是一类特殊的循环矩阵.本文的目的主要是运用多项式因式分解的逆变换研究包含广义Fibonacci、Lucas多项式的关于行斜首加尾右循环矩阵和行斜尾加首左循环矩阵的行列式,结合广义Fibonacci、Lucas多项式的特征给出行列式的显式表达式.首先介绍行斜首加尾右循环矩阵和行斜尾加首左循环矩阵的定义和广义Fibonacci、Lucas多项式的特征性质,然后给出主要的结果和详细过程,最后呈现未研究的结果.

1 预备知识

定义 1.1 通常Fibonacci、Lucas多项式F(x)=Fn(x),L(x)=Ln(x),n=0,1,2,…,定义为二阶线性递推数列:

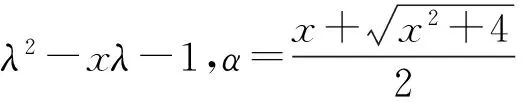
一种广义Fibonacci多项式的通项公式为

广义Lucas多项式的通项公式为

其中

已知

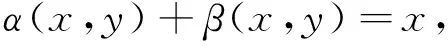
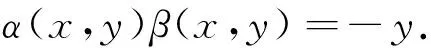
定义 1.2 一个第一行是(a1,a2,...,an)的行斜首加尾右循环矩阵(RSFPLR)为

A=RSFPLRCircfr(a1,a2,...,an)=

也就是说给定任意一行(a1,a2,…,an)作为矩阵的第一行,那么第二行就让第一行的第一个元素加上第一行的最后一个元素,最后一个元素乘以-1,得到的序列所有元素向右移一位,即(-an,a1+an,…,an-2,an-1).任意一行满足以下规则:对第i行的第一个元素加上第i行的最后一个元素;最后一个元素乘以-1;得到序列的所有元素向右移一位得到第i+1行.易知,行斜首加尾右循环矩阵(RSFPLR)是xn-x+1-循环矩阵[3],并且这类矩阵既不是斜循环矩阵的延伸也不是它的特殊情形,而是一种新的特殊矩阵.定义Θ(-1,1)作为基本行斜首加尾右循环矩阵:

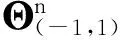
A=RSFPLRCircfr(a1,a1,...,an)=

(1)

A是一个行斜首加尾右循环矩阵,当且仅当

对某一多项式f(x)有

定义 1.3 一个第一行是(a1,a2,...,an)的行斜尾加首左循环矩阵(RSLPFL)为

B=RSLPFLCircfr(a1,a2,...,an)=

给定任意一行(a1,a2,…,an-1,an)为矩阵的第一行,那么第二行用第一行的第一个元素乘以-1,第一行的最后一个元素加上第一行的第一个元素,得到的序列所有元素向左移一位,也就是(a2,a3,…,an+a1,-a1).任意一行满足以下规则:对第i行元素的第一个先乘-1;第i行最后一个元素再加上第i行的第一个元素;所有元素向左移一位得到第i+1行.

引理 1.1 设A=RSFPLRCircfr(a1,a2,…,an),那么A的特征值是

此外

这里ωi,i=1,2,…,n是方程

(2)

的根.

证明 由定义1.2和方程(1)知道A是R行斜首加尾右循环矩阵,当且仅当A与Θ(-1,1)可交换,即

(3)

需证明以下2个特征:

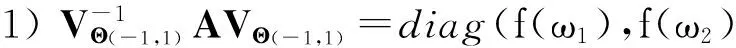
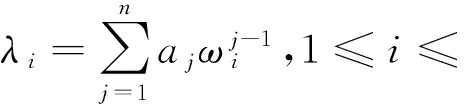
(4)

其中ωi(1≤i≤n)是g(x)=xn-x+1的不同的n个根.

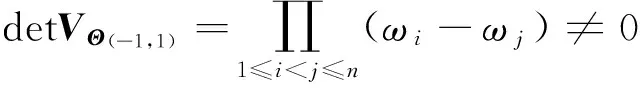
(5)

这里

得

2)由1)的结论可知A的特征值是

因此由矩阵A与它的特征值的关系可得

引理1.1得证.

引理 1.2

证明

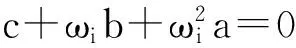
因为ωi(i=1,2,…,n)满足方程(2),则有:

证明 容易验证.进一步有

2 主要结果及证明

定理 2.1 如果C=RSFPLRCircfr(F1,F2,…,Fn),那么

证明 矩阵C=RSFPLRCircfr(F1,F2,…,Fn)可表示为

C=

利用引理1.1,矩阵C为

由引理1.2得

同理可得推论2.1.

D=RSFPLRCircfr(Fn,Fn-1,…,F1)=

类似定理2.1的证明可得

定理 2.2 如果E=RSLPFLCircfr(F1,F2,…,Fn),那么可得

证明 矩阵E=RSLPFLCircfr(F1,F2,…,Fn)可以表示为:

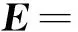
并且

这里D=RSFPLRCircfr(Fn,Fn-1,…,F1),并且它的行列式由推论2.1可知:

因此

detE=detDdetΓ=

考虑广义Lucas多项式Ln的关于行斜首加尾右循环矩阵和行斜尾加首左循环矩阵的行列式的解法.

定理 2.3 如果F=RSFPLRCircfr(L1,L2,…,Ln),那么可得

证明 矩阵F=RSFPLRCircfr(L1,L2,…,Ln)可以表示为

F=

利用引理1.1,F的行列式为

由引理1.2可得

定理2.3得证.同理可得矩阵

G=RSFPLRCircfr(Ln,Ln-1,…,L1),

G=

由定理2.3可得

定理 2.4 如果H=RSLPFLCircfr(L1,L2,…,Ln),那么可得

证明 矩阵H=RSLPFLCircfr(L1,L2,…,Ln)可表示为

H=

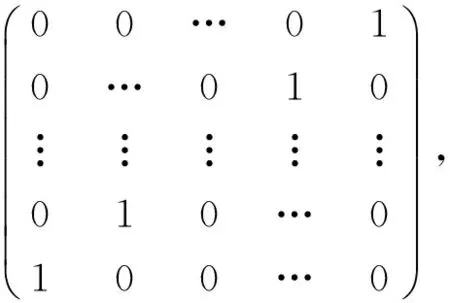
并且

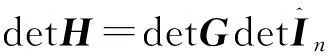
这里G=RSFPLRCircfr(Ln,Ln-1,…,L1),它的行列式在定理2.3中可知,

如果H=RSLPFLCircfr(L1,L2,…,Ln),可得

3 结论

基于这些引理,可知关于行斜首减尾右循环的一些信息,即xn+x+1循环矩阵,同理求广义Fibonacci多项式关于此类循环矩阵的行列式.本文只研究包含广义Fibonacci多项式的行斜首加尾右循环矩阵的行列式.

对广义的Fibonacci、Lucas多项式,当y=1时,可得原始的Finonacci、Lucas多项式;当x=y=1时,可得Fibonacci、Lucas数列;当y=1,x=2时,可得Pell数列.基于本文可以迅速得到Chebyshev多项式,(p,q)-Chebyshev多项式关于行斜首加尾右循环矩阵和行斜首减尾右循环的行列式.本文的理论适用于线性递推数列和多项式,进而研究包含这些数列的循环矩阵的范数,这就证明了文中的所有结论.

4 例子

取x=y=1,n=3,设M=RSFPLRCirc(F1,F2,F3)是包含Fibonacci数列的3×3阶行斜首加尾右循环矩阵

F1=1,F2=1,F3=2,detM=25,由定理2.1的公式可得detM=25.

[1] DAVIS P. Circulant Matrices[M]. New York:Wiley,1979.

[2] 江兆林,周志伟. 循环矩阵[M]. 成都:成都科技大学出版社,1999.

[3] DAVID C. Regular representations of semisimple algebras, separable field extensions, group characters, generalized circulants, and generalized cyclic codes[J]. Linear Algebra Appl,1995,218:147-183.

[4] JIANG Z L, XU Z B. Efficient algorithm for finding the inverse and group inverse of FLSr-circulant matrix[J]. Appl Math Comput,2005,18(1/2):45-57.

[5] TIAN Z P. Fast algorithms for solving the inverse problem ofAx=b[J]. International J Algebra,2011,9:121-124.

[6] MUSTAFA B. On the norms of circulant matrices with the generalized Fibonacci and Lucas numbers[J]. J Pure Appl Math,2015,6(1):84-92.

[7] LI J, JIANG Z L, SHEN N. Explicit determinants of the Fibonacci RFPLR circulant and Lucas RFPLL circulant matrix[J]. Algebra Number Theory Appl,2013,28(2):167-179.

[8] JIANG Z L, LI J, SHEN N. On the explicit determinants of the RFPLR and RFPLL circulant matrices involving Pell numbers in information theory[J]. Information Comput Appl,2012,308:364-370.

[9] TIAN Z P. Fast algorithm for solving the first plus last circulant linear system[J]. Shandong University Natural,2011,46(12):96-103.

[10] JIANG Z L, SHEN N, LI J. On the explicit determinants of the RFMLR and RLMFL circulant matrices involving Jacobsthal numbers in communication[J]. Lecture Notes in Electrical Engineering,2014,272:401-408.

[11] TIAN Z P. Fast algorithms for solving the inverse problem ofAX=bin four different families of patterned matrices[J]. Appl Math Comput,2011,52:1-12.

[12] JAISWAL D V. On determinants involving generalized Fibonacci numbers[J]. Fibonacci Quarterly,1969,7:319-330.

[13] SHEN S Q, CEN J M, HAO Y. On the determinants and inverses of circulant matrices with Fibonacci and Lucas numbers[J]. Appl Math Comput,2011,217:9790-9797.

[14] AKBULAK M, BOZKURT D. On the norms of Toeplitz matrices involving Fibonacci and Lucas numbers[J]. Hacet J Math Stat,2008,37(2):89-95.

[15] JIANG Z L. Efficient algorithm for finding the inverse and group inverse of FLSr-circulant matrix[J]. Appl Math Comput,2005,18(1/2):45-57.

[16] FATIH Y, DURMUS B. Hessenberg matrices and the Pell and Perrin numbers[J]. J Number Theory,2011,131(8):1390-1396.

[17] PREDRAG S,JOVANA N, IVAN S. A generalization of Fibonacci and Lucas matrices[J]. Discret Appl Math,2008,156(14):2606-2619.

[18] ZHANG Z Z, ZHANG Y L. The Lucas matrix and some combinatorial identities[J]. Indian J Pure Appl Math,2007,38(5):457-465.

[19] MILADINOVI M, PREDRAG S. Singular case of genralized Fibonacci and Lucas matrices[J]. J Korean Math Soc,2011,48(1):33-48.

[20] 何承源. 循环矩阵的一些性质[J]. 数学的实践与认识,2001,31(2):211-216.

[21] 曾泳泓.γ-循环矩阵的快速算法和并行算法[J]. 数值计算与计算机应用,1989,10(1):36-42.

2010 MSC：15A18

(编辑 郑月蓉)

Determinants of RSFPLR Circulant Matrices of the Generalized Fibonacci Polynomials

SHI Baijuan

(SchoolofMathematics,NorthwestUniversity,Xi’an710127,Shaanxi)

The main purpose of this paper is to use the inverse factorization of polynomial to give the determinants of RSFPLR circulant matrices and RSLPFL circulant matrices of the generalized Fibonacci polynomials, and the generalized Lucas polynomials. We give the explicit determinants.

generalized Fibonacci polynomials; generalized Lucas polynomials; RSFPLR circulant matrix; RSLPFL circulant matrix; determinant

2016-05-10

国家自然科学基金(11371291)

师白娟(1992—),女,硕士生,主要从事初等数论的研究,E-mail:593800425@qq.com

O177.91

A

1001-8395(2017)01-0022-07

10.3969/j.issn.1001-8395.2017.01.004