基于上下近似与边界域的粗糙集之间的相似度量

钟 诚,王哲河

(海南热带海洋学院 海洋信息工程学院,海南 三亚 572022)

基于上下近似与边界域的粗糙集之间的相似度量

钟 诚,王哲河

(海南热带海洋学院 海洋信息工程学院,海南 三亚 572022)

度量不确定性集合的相似度是粗糙集的核心内容之一.对现有的基于上下近似的粗糙集相似度量方法进行分析,提出一种基于上下近似与边界域的粗糙集间的相似度量公式,并通过例子说明,该方法具有较高的分辨力.

粗糙集;上下近似;边界域;相似度量

0 引 言

粗糙集理论是Pawlak教授于1982年提出的一种能够定量分析处理不精确、不一致、不完整信息与知识的数学工具[1].该理论已成功地应用在机器学习与知识发现、模式识别、数据挖掘、过程与控制、决策支持与分析等方面.粗糙集理论无需提供问题所需处理的数据集合之外的任何先验信息,是通过等价关系的分类以及分类对于目标的近似实现知识发现.知识的不确定性主要是由给定论域里粗糙近似的边界引起的,当边界为空时,知识是完全确定的.边界越大,知识就越粗糙.在实际应用过程中,经常需要比较两种知识模式的一致性或相似性.因此,不同的相似度方法也不断提出[2-6].

文献[2-3]都是基于上下近似集的粗糙集之间相似度量,其中文献[3]对文献[2]的公式加以改进,不但分别考虑了集合间的上、下近似集间的差集,而且又考虑了上下近似集距离的权重.但实际上集合间的边界域距离的大小也会直接影响不确定性集合的相似度,基于这点,本文提出一种基于上下近似与边界域的粗糙集相似度量方法.并通过例子将其与文献[2-3]的基于上下近似的粗糙集相似度量公式进行比较,说明该方法具有更高的分辨力.

1 基本概念

等价关系可以将对象集分类.从认知的角度来看,人们需要通过分类去认识那些不能精确分类表示的对象集,这种集合称为粗糙集.

下面给出有关的基本概念,详细的讨论见文献[1,5,7-11].

设IS=(U,A,V,f)是一个信息系统,U为对象集,A为属性集,f为U和A的关系集,V为属性的值域,B⊆A,x∈U属性B对应的x等价类为：

[x]B={y∈U|f(x,a)=f(y,a),∀a∈B},

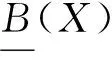
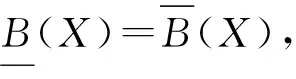
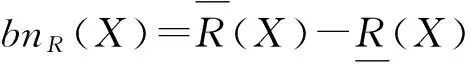
定义1 设(U,R)为近似空间,X,Y⊆U.

1)若RX=RY,则称集合X和Y为R下粗相等,记作X≈RY;

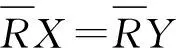
2 粗糙集的相似度量

定义2 设U是一个非空论域,记P(U)为U的所有子集的集合S∶P(U)×P(U)→[0,1],∀X,Y,Z∈P(U),如果S满足:

1)0≤S(X,Y)≤1;

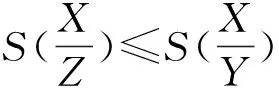
则称S(X,Y)是集合X,Y之间的相似度.

如果将1)换成“当且仅当X=Y时S(X,Y)=1”.则称S(X,Y)是集合X,Y之间的弱相似度.

相似度量是检索两个知识模式一致性以及相似性的一个重要方法,因此,定义一种分辨力较高的相似度量公式是很有必要的.本文将分析文献[2-3]的基于上下近似集的相似度量方法,在此基础上,提出一种基于上下近似与边界域的粗糙集相似度量方法.

2.1 现有的基于上下近似的粗糙集相似度量

定义3[2]设(U,R)为近似空间,∀X,Y⊆U定义

(1)

定义4[3]设(U，R)为近似空间,∀X，Y⊆U，α,β∈[0,1],α+β=1.定义

(2)

经研究,发现定义3只是考虑了粗糙集间的上、下近似的差集,而定义4不但考虑粗糙集间的上、下近似的差集,而且考虑了上、下近似的差集对集合间的相似度量的影响,并引入了权重计算.边界域的大小会影响集合的粗糙度,所以粗糙集间的边界域的差集也会影响粗糙集间的相似度,而定义3,4都没有考虑粗糙集间的边界域的差集对相似度的影响.因此,本文将提出一种基于上下近似集与边界域的粗糙集间的相似度量方法.

2.2 基于上下近似与边界域的粗糙集相似度量

为了方便叙述下文的基于上下近似集与边界域的粗糙集相似度量公式,先给出边界域距离的定义.

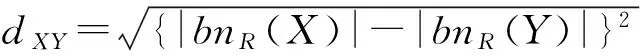
由定义5可得到以下性质.

定理1 设(U,R)为近似空间,∀X,Y⊆U,则有以下性质成立.

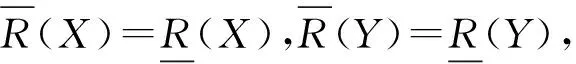
证明 由定义5,显然性质1)成立.

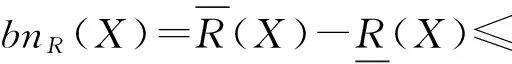
推论1 若X=Y=φ,则dXY=0.

定义6 设(U,R)为近似空间,∀X,Y⊆U,α,β,γ∈[0,1],α+β+γ=1.定义

(3)

下面定理的结果是一种相似度量.

定理2 设(U,R)为近似空间,则∀X,Y⊆U,S(X,Y)为X与Y关于等价关系R的相似度.

证明 显然S(X,Y)满足定义2中的1)-3),下面证明其满足定义中的条件4).

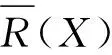
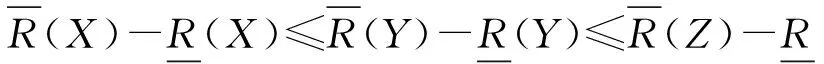
所以

故S(X,Y)≥S(X,Z).同理可证:S(Y,Z)≥S(X,Z).

性质1 设(U,R)为近似空间,则S(U,φ)=0.

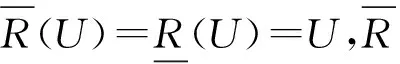
推论2 设(U,R)为近似空间,∀X⊆U,S(X,φ)=0.

性质2 设(U,R)为近似空间,∀X,Y⊆U∧X≈RY,则S(X,Y)=1.

证明 由定义2及定义5,即可证该性质成立.

性质3 设(U,R)为近似空间,∀X,Y⊆U,且X,Y是关于R的精确集,则

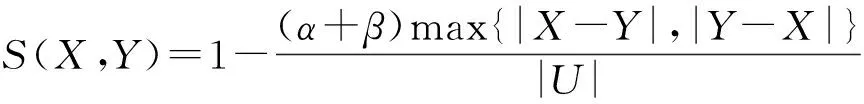
证明 若X,Y是关于R的精确集,则

故由定义5可证.

3 算例分析

下面给出一个具体的例子.

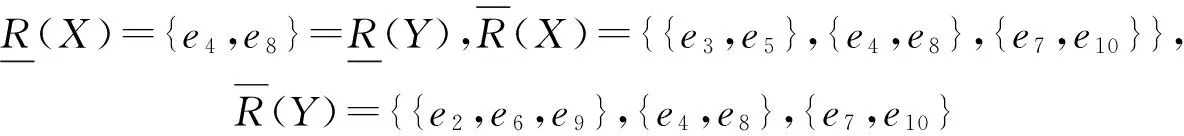
所以有

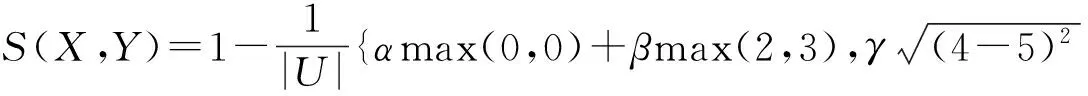
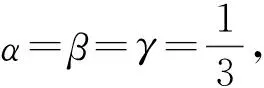
利用文献[2]定义的相似度量即式(1)可得:

利用文献[3]定义的相似度量即式(2)可得:

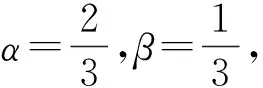
从结果可以看出,由式(1)计算得的两个集合的相似度太低,而式(2)又太高,由式(3)计算得到的相似度更贴近实际.

4 结 语

本文在现有的上下近似集粗糙相似度量方法研究的基础上,讨论了边界域对不确定性集合相似度的影响,并提出一种基于上下近似集与边界域的粗糙集合间的相似度量方法.最后通过例子进行验证,本文所提出的相似度量方法具有更高的分辨力.

[1]Pawlak Z.Rough Sets [J].International Journal of Computer and Information Sciences, 1982, 11(5):341-356.

[2]刘文军,赵利萍.粗糙集的相似度量[J].数学理论与应用.2012,32(3):35-42.

[3]林娟,米据生,解滨.粗糙集的两种相似性度量[J].计算机科学.2015,42(6):79-100.

[4]张清华,王进,王国胤.粗糙模糊集的近似表示[J].计算机学报,2015,38(7):1484-1494.

[5]徐久成,沈均毅,王国胤.Rough集之间的相似度量[J].计算机科学,2003,30(10):55-60.

[6]史占红,连玉平.基于包含度的粗糙集间的相似性度量[J].数学教学研究,2008,27(2):53-54.

[7]张文修,吴伟志,梁吉业,等.粗糙集理论与方法[M].北京: 科学出版社, 2008.

[8]王国胤,姚一豫,于洪.粗糙集理论与应用研究综述[J].计算机学报,2009,32(7):1229-1243.

[9]徐伟华.序信息系统与粗糙集介绍及研究综述[J].琼州学院学报,2014,21(5):12-16.

[10]李敬,王利东,李晓庆,等.基于优势度的序信息系统属性重要性度量[J].琼州学院学报,2015,22(5):17 -22.

[11]张文修,梁怡,徐萍,等.基于包含度的不确定性推理[M].北京:清华大学出版社,2007.

(编校：曾福庚)

Similarity Measures between Rough Sets Based on theLower and Upper Approximation and Boundary Domain

ZHONG Cheng, WANG Zhe-he

(School of Ocean Information Engineering, Hainan Tropical Ocean University, Sanya Hainan 572022, China)

Measuring the similarity of the uncertain set is one of the cores of the rough set.The analysis was conducted on the current rough set similarity measuring methods based on the lower and upper approximation.Consequently, a similarity measuring formula between rough sets on the basis of the lower and upper approximation and boundary region was proposed.Examples showed that the method has a higher resolution.

rough set; lower and upper approximation; boundary region; similarity measure

格式：钟诚,王哲河.基于上下近似与边界域的粗糙集之间的相似度量[J].海南热带海洋学院学报,2017，24(2)：39-42.

2016-11-01

海南热带海洋学院青年科研基金(QYQN201515，QYQN201428)

钟诚(1981-),男,海南昌江人,海南热带海洋学院海洋信息工程学院讲师,硕士,主要研究方向为粗糙集、数据处理.

TP18; O159

A

2096-3122(2017) 02-0039-04

10.13307/j.issn.2096-3122.2017.02.08