预测模型下模糊控制实时任务调度算法

乔 付

(海南热带海洋学院 海洋信息工程学院,海南 三亚 572022)

预测模型下模糊控制实时任务调度算法

乔 付

(海南热带海洋学院 海洋信息工程学院,海南 三亚 572022)

现有实时任务调度算法的性能指标相对比较单一,如只考虑利用率问题,忽略了任务丢失率这项关键性能指标.因此,本文提出同时考虑到节点的利用率和任务丢失率,使用预测信息来进一步提高系统的实时性能,在反馈控制实时系统模型中增加一个预测模型,并使用模糊控制策略实现实时任务调度.最后,通过实验验证所提模糊控制实时任务调度算法性能.

实时任务调度;模糊控制;预测模型

0 引 言

一个大型的应用程序通常要被划分成多个任务并被分配到不同的计算节点上进行计算,在没有实时任务调度算法的配合下,计算节点就会把这些任务按照到达的顺序进行排队,不会考虑有时间要求任务的计算问题.

实时任务调度算法分为静态和动态实时任务调度算法两种[1-5].静态实时任务调度算实现已知任务集和它的约束,如截止期限[6]等.RM(Rate Monotonic)算法是静态实时任务调度的代表算法;而动态实时任务调度算法不知道具体的任务集和相关的约束,例如,有新的任务加入时,动态实时任务调度算法不知道当前正在调度的具体任务,也不知道任务的具体完成时间.

多数调度理论和算法都是基于周期任务模型或随机任务模型[7-8],且都是从任务级角度研究其调度问题,也有从功能级模型研究任务间的调度问题,但仅限于简单的分布式功能[9-12].文献[2]提出一种类似RM算法的静态实时任务调度算法,该算法对现有已知任务的约束要求严格.文献[3]所述动态实时任务调度算法的典型代表算法是EDF算法,但是该算法在资源不足时表现出来的性能欠佳.上述算法均属于开环调度算法,不适合在反馈控制调节系统中应用.传统的控制系统设计和实现的方法是把控制和调度分开的,不能确保提供控制质量,从资源调度的角度看,应用到实时调度的开环实时调度算法缺乏灵活性,如文献[13]提出的开环控制调度算法;文献[14]提出按照最大偏差的任务优先策略对任务进行调度,其需要不断地执行排序算法,使系统算法的复杂度增加;文献[15]提出了适合小规模的实时任务调度算法;文献[16]提出一种反馈实时控制任务的调度架构,使用反馈信息调节负载,优化整体性能,其缺点是采样时间间隔过于精确,使得系统不好控制;文献[17]侧重按照控制应用程序的动态性,使用新的调度策略来控制系统性能;文献[18]的预测模型不是在时间约束下考虑的模型;文献[19]提出一种模糊实时任务调度算法,该算法适合在不可预测情况下的实时任务调度,也就不能使用预测信息来调节反馈控制器;文献[5]提出的模糊反馈控制调度算法同样也忽略了使用预测信息,并且该算法只侧重于利用率,没有关注任务丢失率问题;文献[20]虽然考虑了任务丢失率问题,但其也是没有使用预测信息.

因此,为提高实时性能在反馈控制模型中引入预测模型,给出预测模型算法,设计了PID控制器,分析了其稳定性,基于该控制器提出一种模糊控制实时任务调度算法.

1 模糊控制实时任务调度算法

1.1 预测的模糊控制实时系统模型

图1 预测模糊控制模型

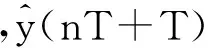
(1+a1x-1+a2x-2+…+anx-n)y(nT)=(b1+b2x-1+…+bmx-m+1u(nT)+(c0)+c1x-1+…+cpx-p)ξ(nT)+d,

(1)

其中：n(nT)是控制器的输出;y(nT)是处理后输出;d是偏移量,ξ(nT)是噪声.

不失一般性,令d=0,ξ(nT)=0.为方便,把式(1)写成如下形式：

Ap×(m+n)X(n+m)×1=Yp×1，

(2)

其中：y,bi,ai的个数分别是p,m,n.

根据式(2),X(n+m)×1有如下三种表示方法：

(3)

不妨定义J为下面的形式：

(4)

其中:e(nT-iT)=r(nT-iT)-y(nT-iT)表示r(nT-iT)与y(nT-iT)之间的误差;Δu(nT-jT)表示输出增量;h1,h2表示预测界限和控制界限.

1.2 模糊PID控制器设计

图1虚线框内的PD+I控制器的转移函数为：

UPID(S)=UPD(s)+U1(S),

(5)

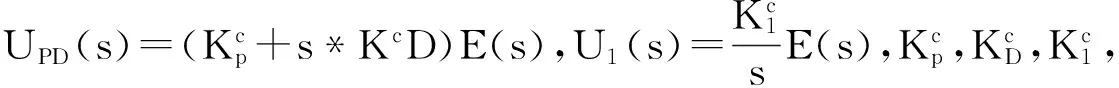
从图1设计的PD+I控制器,可知：

还可以推出：

ΔUPD(nT)=Kp*d(nT)+KD*r(nT),ΔUI(nT)=K1*r(nT)+K1*e(nT-T),

UPD(nT)=-UPD(nT-T)+KUPD*ΔUPD(nT),U1(nT)=U1(nT-T)+KU1*ΔU1(nT),

图1中的PD+I控制器的转移函数表示为：

UPID(nT)=UPD(nT)+UI(nT).

(6)

对于模糊化PD控制器过程,图2和图3分别为输入和输出的隶属函数,可以把输入空间分成如图4的20个组合区域,PD控制器使用下面的四个模糊控制规则：

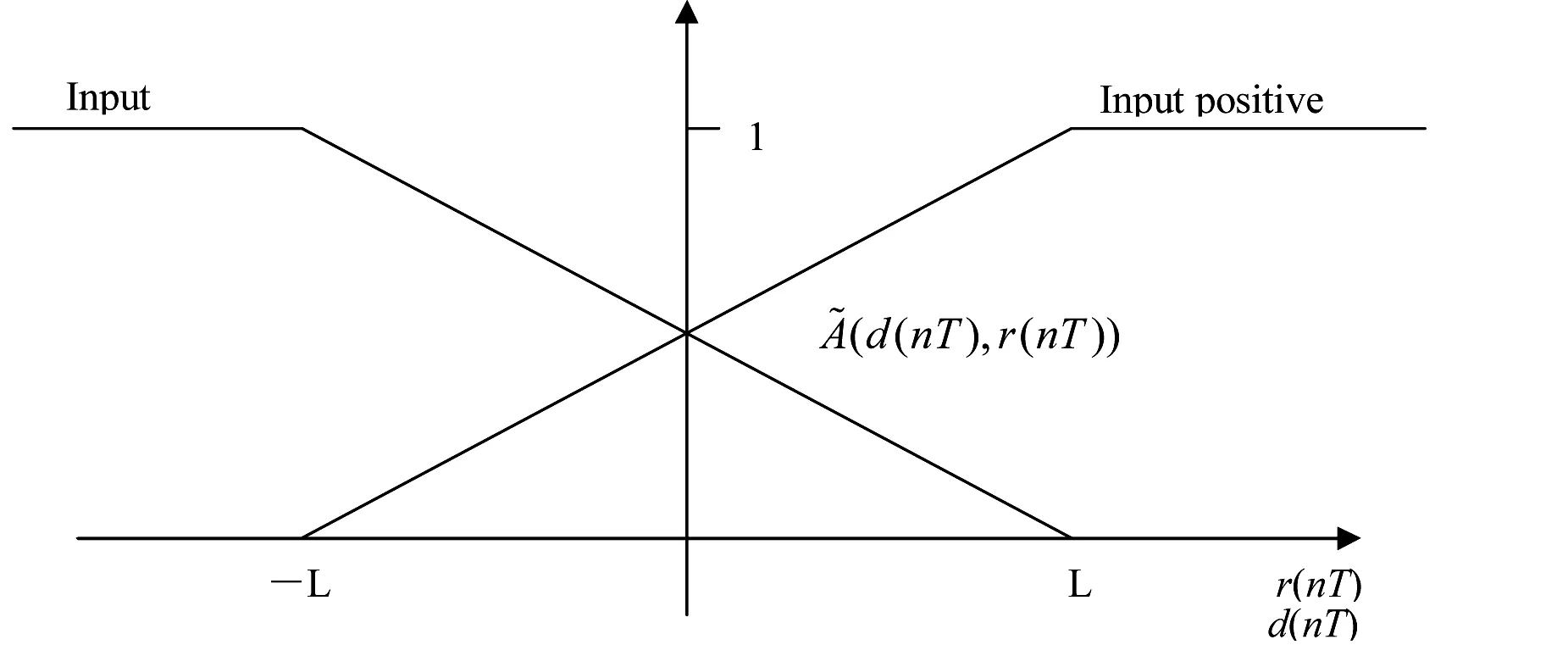
图2 模糊PD控制器的输入隶属函数

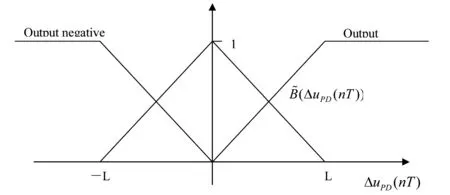
图3 模糊PD控制器的输出隶属函数

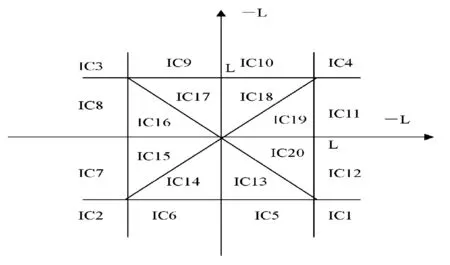
图4 模糊PD控制器的输入组合区域

规则1：IFd=d.nANDr=r.nThenPD-output=o.p,

规则2：IFd=d.nANDr=r.nThenPD-output=o.n,

规则3：IFd=d.pANDr=r.nThenPD-output=o.p,

规则4：IFd=d.pANDr=r.pThenPD-output=o.z,

其中:d.p表示正误差,d.n表示负误差,r.p表示正误差率,r.n表示负误差率,o.p和o.n分别表示正负输出,o.z表示零输出,AND是扎德模糊算子.

模糊化质心表示成如下形式：

(7)

应用输出隶属度值o.p=L,o.n=-L,o.z=0和图4中的直线方程可以得到：

因此,图4的IC1～IC20范围的有关模糊PD控制器的ΔuPD(nT)值可求：

同理,对于模糊I控制器,也有类似如图2和图3的输入和输出隶属函数,可以把输入空间分成类似如图4 的20个组合区域,并有如下的模糊规则：

规则5：IFe(nT-T)=e.nANDr=r.nThenI-output=o.n,

规则6：IFe(nT-T)=e.nANDr=r.pThenI-output=o.z,

规则7：IFe(nT-T)=e.pANDr=r.nThenI-output=o.z,

规则8：IFe(nT-T)=e.pANDr=r.pThenI-output=o.p.

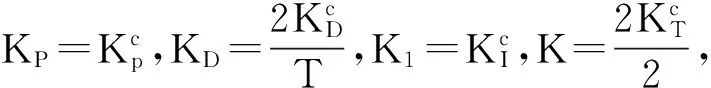
1.3 模糊PID控制器稳定性分析

分析控制器的稳定性方法很多,这里采用Lyapunov’s第二方法[13]来分析所设计的PD+I控制器.按照Lyapunov’s第二方法,该控制器可以表示为：

(8)

其中：x是状态向量,θ是干扰,u是控制器,y系统输入,f(x),F(x),g(x),h(x)是非线性函数.

式(8)要保持如下的参考系统：

(9)

所设计的可预测模糊PD+I控制器的输入J的两个目标为

J(nT)的误差：eJ(nT)=J(nT)-Jr(nT);

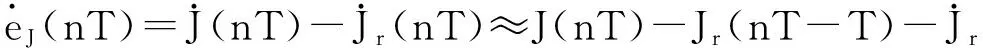
当y=h(x)=x,h(xr)=xr时,式(8)减去式(9)可得：

e=y-yr=x-xr,

(10)

可令ef=f(x)-fr(xr),eF=F(x)-Fr(xr),则有：

(11)

∃α1,α2,α4,α5,α6,α7,β1,β2,β3,β4,β5<0的常量,且满足如下条件：

按照上面的条件所设计的预测控制系统是稳定的.

该预测模型的建模架构如图5所示,选择控制参数U={u1,u2,…，uN}用来定义每一个解决器,对应的参考输入R=(r1,r2,…，rM),即为给定的问题事例,f1,f2,…，fN为可供选择的N个不同配置的模型.模型fi使用动态的信息y(k)预测R={r1,r2,…，rM}的最好参数.例如,在第一个采样间隔里选择了u1∈U,如果预测可以得到较好的参数性能,则可继续切换到u2,u3,…，uN∈U.从一个参数的配置模型切换到另一个参数的配置模型,当从u1到u2切换时,u1的处理暂停并保留现场,恢复u2的处理现场.该预测模型还要满足两个条件,第一,可以使用建模后事例的解决器性能参数预测新的事例性能参数;第二,如果在两个事例所使用的解决器相同,那么该解决器可以用来继续执行这两个事例的其它处理操作.

基于这两个条件,可以按如下步骤描述出该预测模型算法PMA(PredictionModelAlgorithm)：

1) 初始化时为每一个由参数配置μ1∈U的解决器给定时间上限T.

2) 由每一个解决器记录每一个采样间隔的优化参数配置情况,yij(k)表示第j个事例rj的第k个采样间隔的第i个解决器所得到的优化参数方案,此过程没有发生切换.

4) 计算Dj(r,k)的最小距离min{Dj(r,k)},求得min{Dj(r,k)}所对应的事例IOPT的参数配置模型,使用该参数配置模型预测执行事例ri的参数配置情况.

5) 在下一个采样时间间隔,使用解决器参数配置u(k+1)来预测在给定时间上限T内的最终结果.

6) 在每个采样时间间隔重复上述过程.

1.4 模糊控制任务调度算法描述

不妨取误差E、误差变化率ECR和控制输入U的模糊集合分别为

E={NB,NM,NS,NZ,PZ,PS,PM,PB},

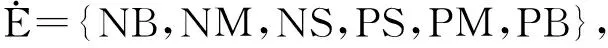
U={NB，NM，NS，ZE，PS，PM，PB},

其中：NB=负大,NM=负中,NS=负小,NZ=负零,PZ=正零,ZE=零,PS=正小,PM=正中,PB=正大.

e={-6,-5,-4,-3,-2,-1,-0,+0,+1,+2,+3,+4,+5,+6},

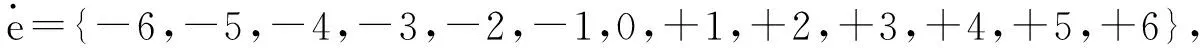
u={-7,-6,-5,-4,-3,-2,-1,0,+1,+2,+3,+4,+5,+6,+7}.

使用表1的控制规则,采用Min-Max模型使用最大隶属度方法求出控制决策表,将该控制决策表存储起来,供运行时查找使用.

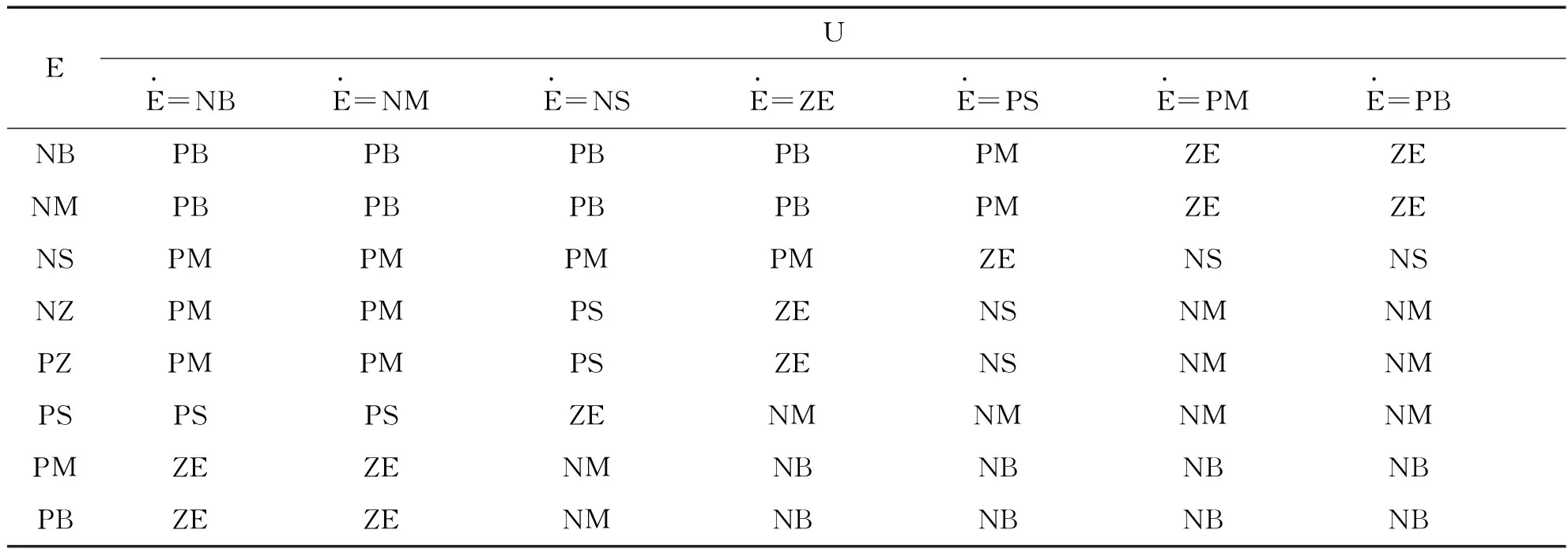
表1 模糊控制规则表

模糊控制实时任务调度算法(FUCRTSA：FuzzyControlReal-timeTasksSchedulingAlgorithm)步骤如下：

1)当有新的任务进入,计算当前节点的利用率和任务丢失率,并执行这个新任务.

2)当有任务退出,释放任务所占用资源,同时计算当前节点利用率和任务丢失率.

2 实验结果与分析

模拟实验平台为一台PC机,基本参数：处理器是AMD X2 240、内存是4GB, Windows 10操作系统.比较本文所提出的FUCRTSA算法与文献[5,20]算法的性能,文献[5]提出的模糊反馈控制调度算法没有使用预测信息,并且该算法只侧重于利用率,没有关注任务丢失率问题.

实验中选择了计算节点利用率和任务丢失率作为衡量指标,图6为运行三个算法的计算节点利用率比较,图7为运行三个算法的任务丢失率比较.在实验中,有足够多的任务供系统去执行,预测利用率为80%,任务丢失率为2%.从图6中可以看出,三个算法在取得计算节点利用率达到稳定的时间有很大区别,使用FUCRTSA算法在19秒时开始使得利用率达到了90%,使用文献[20]算法在24秒时开始使得利用率达到了90%,使用文献[5]算法在28秒时开始使得利用率达到了90%.另外,在0-5秒时,文献[5]算法所取得的利用率变化不大,而其它两个算法取得的利用变化较大.

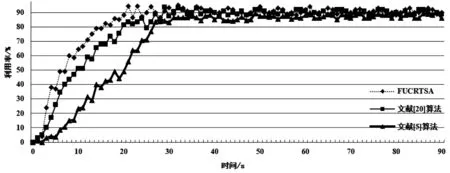
图6 使用三个算法的计算节点利用率比较

从图7中可以看出,三个算法几乎在同一时间得到稳定的任务丢失率状态,但使用FUCRTSA算法所取得的任务丢失率维持在1%左右,使用文献[20]算法所取得的任务丢失率维持在1.8%左右,使用文献[5]算法所取得的任务丢失率维持在2%左右.

综合上述实验结果,在计算节点利用率和任务丢失率上FUCRTSA算法要好于文献[20]算法和文献[5]算法.这是由于文献[20]算法和FUCRTSA算法都是用了闭环控制,而文献[5]算法使用的是开环控制的结果,而且FUCRTSA算法中使用了预测信息来处理反馈信息,使得FUCRTSA算法性能要好于文献[20]算法.

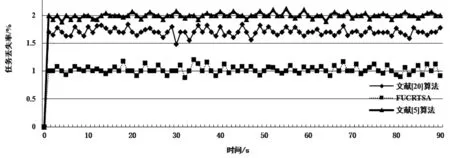
图7 使用三个算法的任务丢失率比较

3 结论

解决了网格计算中实时任务调度问题,考虑到预测信息可以提高实时性,在反馈控制模型中引入了预测模型,设计了模糊PID控制器,并分析其稳定性,提出了模糊控制实时任务调度FUCRTSA算法.实验表明：在利用率和任务丢失率两个性能指标上FUCRTSA算法优于文献[20]和文献[5]中算法,而文献[20]中算法又优于文献[5]中算法.

[1]Park SM, Humphrey M.Feedback-controlled resource sharing for predictable eScience[C]//Proc of the 2008 ACM/IEEE conference on supercomputing.New York:IEEE press, 2008:15-21.

[2]Ayav T, Sorel Y.Feedback control static scheduling for real-time distributed embedded systems[C]//Proc of the 11th IEEE IntConf on Embedded and Real-Time Computing Systems and Applications.New York:IEEE press, 2005:173-176.

[3]Baker T P.An analysis of EDF schedulability on a multiprocessor[J].IEEE transactions on parallel and distributed systems, 2005, 16(8):760-768.

[4]殷月竹,殷志祥,许锋,等.单输入时滞离散系统的LQR问题[J].合肥工业大学学报(自然科学版),2008, 31(12):2072-2076.

[5]Xia F.Feedback scheduling of real-time control systems with resource constraints [J].JCS&T,2007, 7(3):263-267.

[6]黄丽达,李仁发.截止时限为关键参数的混合关键级实时任务调度研究[J].计算机研究与发展, 2016, 53(7): 1641-1647.

[7]Lakshmanan K,De Niz D, Rajkumar R.Mixed-criticality task synchronization in zero-slack scheduling[C]//Proc of IEEE Real-Time and Embedded Technology and Applications Symp.New York:IEEE press, 2011:47-56.

[8]Dorin F, Richard P, Richard M, et al.Schedulability and sensitivity analysis of multiple criticality tasks with fixed-priorities[J].Real-Time Systems, 2010, 6(3):305-331.

[9]Zeller M, Prehofer C, Weiss G, et al.Towards self-adaptation in real-time, networked systems:Efficient solving of system constraints for automotive embedded systems[C]//Proc of IntConf Self-Adaptive and Self-Organizing Systems.New York:IEEE press, 2010:79-88.

[10]Katoen J P, Noll T, Wu H, et al.Model-based energy optimization of automotive control systems[C]//Proc of the Conf on Design, Automation and Test in Europe.New York:IEEE press, 2013:761-766.

[11]Hernrich P, Prehofer C.Network-wide energy optimization for adaptive embedded systems[J].ACM SIGBED Review, 2013,10(1):33-36.

[12]Xie G, Li R, Xiao X, et al.A high-performance dag task scheduling algorithm for heterogeneous networked embedded systems[C]//Proc of IEEE IntConf on Advanced Information Networking and Applications.New York:IEEE press,2014:1011-1016.

[13]Sahoo D R,Swaminathan S, et al.Feedback control for real-time scheduling[C]// Proceedings of the 2002 American Control Conference.New York:IEEE press, 2002: 1254-1259.

[14]Yepez J, Josep M.Fuertes, Pau Marti.The large error first (LEF) scheduling policy for real-time control systems[EB/OL].(2009-11-9)[2016-11-5].http://dcs.upc.edu/uploads/publications/f1fd9a72bb792dcd7a23b159c4dca8bb.pdf.

[15]Ying L, Crawford S L, Wheeler Ruml, et al.Feedback control for real-time solving[C]//Proceedings of CP2004 workshop.NewYork:IEEE press,2004, 9:1-15.

[16]CervinA,Eker J, Bernhardsson B, et al.Feedback-Feedforward Scheduling of Control Tasks[J].Real-Time Systems, 2002, 23(1):1-15.

[17]Marti P, Fohler G, Ramamritham K, et al.Improving quality-of-control usingflexible timing constraints: metric and scheduling[C]//Proceedings of Real-Time Systems Symposium.New York:IEEE press, 2002: 91-100.

[18]Nudelman E, Devkar A, Shoham Y, et al.Understanding random SAT: beyond the clauses-to-variables ratio[C]// Proceedings of constraint programming.New York:IEEE press2004:438-452.

[19]金宏,王宏安,傅勇,等.模糊反馈控制实时调度算法[J].软件学报,2004,15(6):791-798.

[20]乔付.具有模糊多目标网格任务调度算法[J].计算机工程与科学,2013,36(9):1644-1649.

(编校：曾福庚)

Fuzzy Control Real-Time TasksScheduling Algorithm Based on Prediction Model

QIAO Fu

(School of Ocean Information Engineering, Hainan Tropical Ocean University, Sanya Hainan 572022,China)

The performance indices are relatively single in existing real-time tasks scheduling algorithms.For instance, if only the utilization rate is considered, the tasks loss rate that is a key performance index is ignored.Therefore in this paper the utilization rate and loss rate were considered simultaneously, and the real-time performance of the system was improved by the use of the prediction information.Moreover, a prediction model was added to the feedback control real time system model, and fuzzy control strategy was used for real-time tasks scheduling.Finally, the performance of the proposed fuzzy control real-time tasks scheduling algorithm was verified by the experiments.

real-time scheduling; fuzzy control; prediction model

格式：乔付.预测模型下模糊控制实时任务调度算法[J].海南热带海洋学院学报,2017，24(2)：47-54.

2016-10-07

乔付(1975-)，男，黑龙江依安人，海南热带海洋学院海洋信息工程学院副教授，博士，主要研究方向计算机视觉和并行计算.

TP393.028

A

2096-3122(2017) 02-0047-08

10.13307/j.issn.2096-3122.2017.02.10