基于MUSIC与FOA的异步电动机转子断条故障检测
史丽萍,吴文军,马晓伟,张玉鸿
(1.中国矿业大学,徐州221008;2.国网四川省电力公司经济技术研究院,成都610041)
0 引 言
异步电动机转子断条故障是常见电机故障之一,它将导致电动机运行性能下降,严重时电机会因此无法驱动负载而出现堵转、停转,甚至烧坏电机,威胁工业生产的可靠性和安全性,同时增加生产成本[1]。因此对该故障进行及时可靠的检测颇为重要。
基于定子电流特性分析(以下简称MCSA)是异步电动机转子断条故障在线诊断的常用方法。研究表明,定子电流中包含电机的故障特征,因而通过提取定子电流故障特征可以准确地检测电机故障[2]。例如当异步电动机定子电流中出现(1±2s)f1频率分量(f1为供电频率,即定子电流基频分量,s为转差率)时,电机则发生转子断条故障,因此在判断转子断条故障时可以对该边频分量进行检测[3]。
常用的边频分量检测方法有Park矢量变换、瞬时功率法和快速傅里叶变换(以下简称FFT)等。这些方法都可以在一定程度上有效检测转子故障。但是Park矢量变换及其改进策略是基于定子三相电流信号的方法,而瞬时功率法不仅需要采集定子电流信号还需要电压信号,这无疑大大提高了硬件要求,导致成本增加[4]。在异步电机转子断条故障检测中,FFT是最常用的电流特性分析方法。但是当电机负载比较小时,转差率s非常低,边频分量(1±2s)f1极其接近基频f1,为了确保检测精度,就必须保证具有足够长时间的采样信号,同时边频分量的幅值较基频很小且由于噪声干扰,这就导致边频分量极易被淹没,频谱泄露在所难免,此时基于FFT的定子电流特征分量检测方法的灵敏度便会大打折扣[5]。而且,只有当定子电流信号以及负载在较长时间内保持平稳时此方法才有效,一旦负载波动太大,其检测准确性将严重恶化[6]。
多重信号分类(以下简称MUSIC)是比较常用的现代谱估计技术,在相同的采样点数或采样时长情况下,其明显比FFT具有更好的频率分辨力,尤其是对于短数据情况更能彰显其高分辨率的优越性。对于负载波动、噪声干扰情况下的异步电机故障诊断,该方法十分行之有效[7]。
通过计算得到感应电动机转子断条故障时基波成分的幅值以及边频分量的幅值,然后将二者之比定义为转子断条故障严重系数,从而反映电机的故障程度[8]。MUSIC虽能够准确估计特征信号的频率,但其不能提供特征信号的幅值和初相角。为了确定各个频率的幅值、初相角,群体智能优化算法被引入。如模式搜索算法(PSA)、粒子群优化算法(PSO)以及模拟退火算法(SAA)等是比较流行且效果不错的方法。2011年,台湾学者Wen-Tsao Pan提出了果蝇算法(以下简称FOA)[9],因其具有算法简单、参数少、易调节、实时性好等优点引起了广泛关注,并应用于不同领域,但是在迭代过程中盲目搜索,容易陷入局部最优,且后期收敛速度慢等是该算法的严重缺陷[10-12]。文献[12]对其进行了诸多改进策略,其改进策略解决了FOA定义域不能为负值的问题,同时提高了算法全局寻优能力和收敛速度,相比SAA等耗时更少。
本文首先以转子断条故障仿真信号测试FFT和MUSIC的频率分辨力,结果表明MUSIC的频率检测精度很高,然后采用SAA和FOA对仿真信号进行幅值、初相角估计,表明FOA具有更好的精度与收敛速度。最后,采用 MUSIC与 FOA对一台Y132M-4型感应电机进行实验验证。实验结果表明,采用MUSIC与FOA相结合的异步电动机转子断条故障检测方法是行之有效的。
1 MUSIC
1.1 基本理论
MUSIC是一种基于矩阵特征值分解的方法,其原理如下[13]:
采样信号x(n)用p个谐波分量的组合表示:
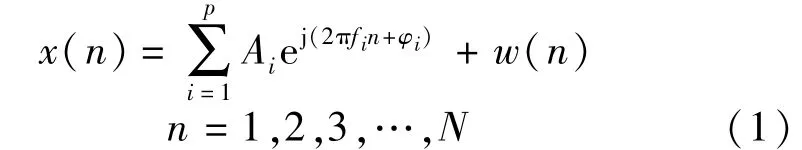
式中:p,N分别为谐波个数和采样点数;fi,Ai,φi则表示第i个谐波的频率、幅值、初相角;w(n)为零均值、方差为σ2的白噪声。
引入一个m×N阶矩阵(一般取m=3N/4以保证m≥p)。
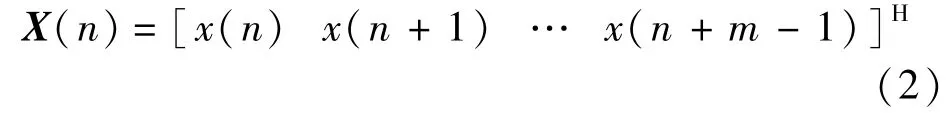
则X(n)的自相关矩阵:
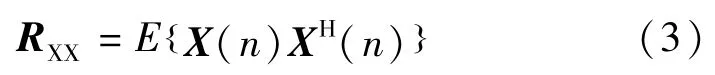
式中:H表示共轭转置;E表示数学期望。
MUSIC算法的步骤如下:
步骤1:构造相关矩阵RXX并将其进行特征值分解。
步骤2:将步骤1中的特征值按降序排列,同时定前p个为主特征值,后m-p个为次特征值σ2,然后求出所有特征值对应的特征向量vi(i=1,2,3,…,m)。
步骤3:构造谱估计表达式:
式中
步骤4:取fi=Δf,计算P(fi)。Δf即为频率分辨率,本文取值为0.001 Hz。
步骤5:根据计算结果搜索出最大的p个峰值所对应的频率f1,f2,…,fp即为所求。
1.2 基于转子断条仿真信号的MUSIC性能分析
采用式(4)模拟异步电动机转子断条时定子电流信号:

采用MUSIC与FFT分别对该模拟信号进行分析,其结果如表1所示。此时转差率s=0.2%,采样频率Fs=5 kHz。表中给出N1=50 000(时长10.0 s),N2=7 500(时长1.5 s)两种情况下MUSIC与FFT的计算结果。
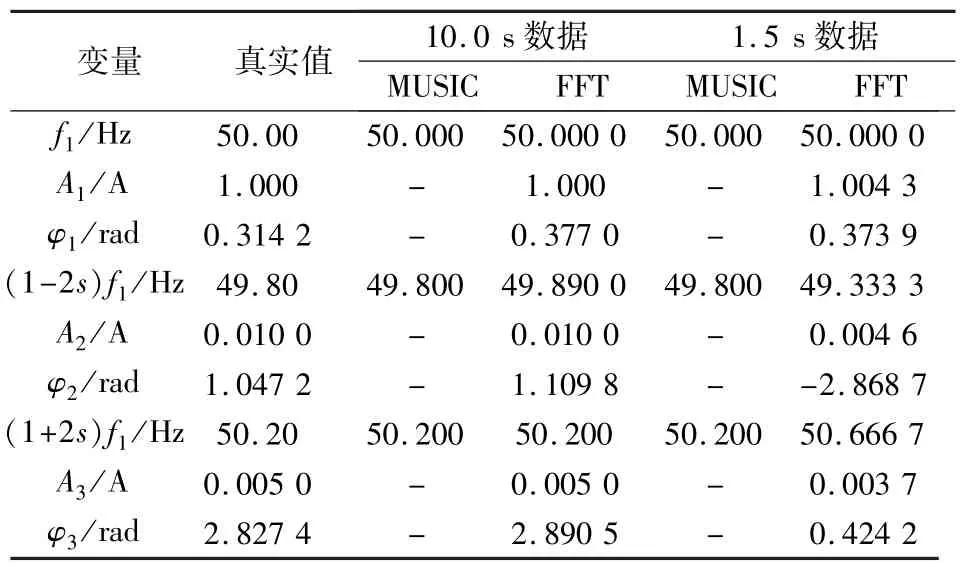
表1 MUSIC与FFT算法的性能比较
表1表明,MUSIC对采样信号具有更高的频率估计精度,尤其对于短数据情况,MUSIC的频率分辨力丝毫不受影响,而FFT则因频谱泄露不能精确计算各特征分量的频率和幅值。
由此可知,MUSIC可以准确检测出断条故障时定子电流中包含的故障特征信息,且能够有效克服因为负载波动、噪声干扰等影响故障特征频率难以准确提取的弊端。但MUSIC对于特征信号的频率和相位估计则无能为力,导致其无法判断转子断条严重程度。此问题亟须解决。
2 FOA
2.1 基本理论
FOA同其它群体智能优化算法一样,也是基于生物的行为过程而抽象演变出来的一类具有全局寻优能力的新智能算法[14]。由于嗅觉和视觉系统比大多数动物发达,果蝇首先依靠嗅觉搜集漂浮在空气中的各种食物的气味,然后以此为建立导向,一步一步向食物所在位置靠拢,充分发挥其视觉的优越性,最终发现食物与同伴的聚集地[15]。但是基本FOA不能求解定义域包含负数的情况,导致其不能正确求解特征分量的幅值、初相角。文献[10]对基本FOA进行了相应的改进,本文便采用其改进的FOA进行幅值、初相角的求解。其主要步骤如下:
步骤1:参数初始化
设定果蝇群体规模SizePop,最大迭代次数Maxgen,搜寻系数n,初始权重系数w0,权重调整系数α。
步骤2:候选解的线性产生机制
步骤2.1:初始化果蝇群体位置
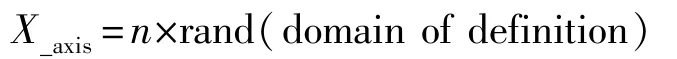
步骤2.2:赋予果蝇个体利用嗅觉搜寻食物的随机方向和距离
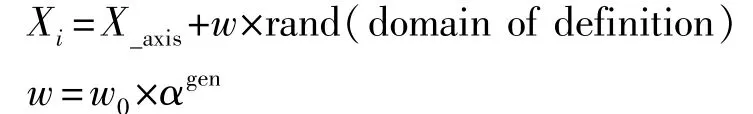
步骤2.3:计算味道浓度判定值
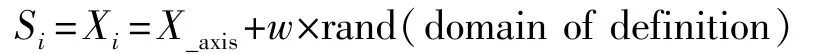
步骤3:将Si代入适应度函数Function中求出果蝇个体的气味浓度值Smelli

步骤4:找出果蝇群体中表现为味道浓度最佳的个体

步骤5:将最佳气味浓度值保存下来,并令最大气味浓度值的果蝇的位置X_axis成为下一次迭代时果蝇群体的初始位置
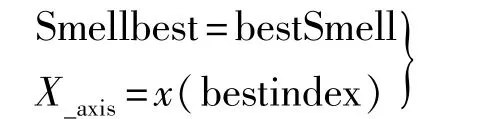
步骤6:进入迭代寻优,直到满足终止条件。
2.2 基于转子断条仿真信号的FOA性能分析
首先利用MUSIC确定采样信号x(n)各成分的频率fi,然后采用FOA估计各成分的幅值Ai、初相角φi(i=1,2,3,…,p)。
工程上,式(1)的信号可以转化:

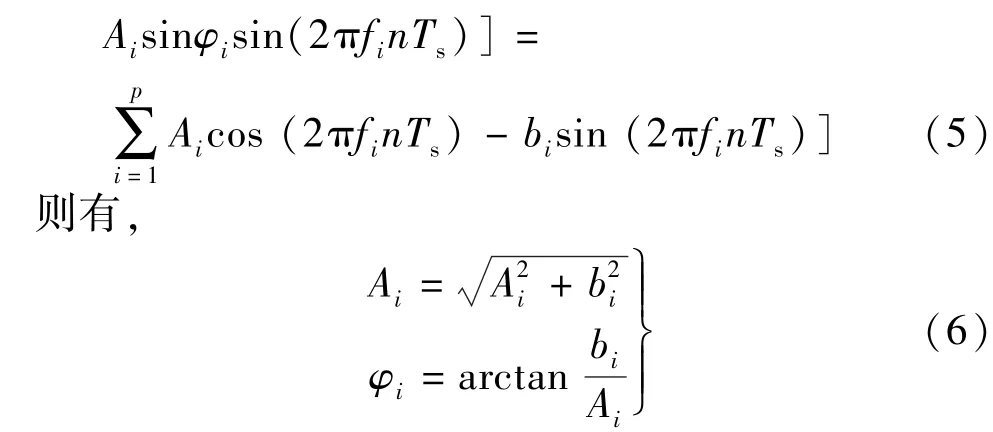
令y1(n),y2(n)为p×N矩阵:
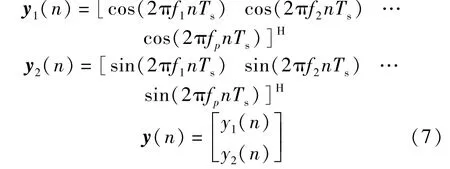
式中:n=1,2,3,…,N。
同理,令X=(A1A2…Apb1b2…bp)。由于x(n)和y(n)都是已知,则目标函数可设:通过式(8)便可以求解X,进而可以得到幅值Ai,初相角φi(i=1,2,3,…,p)。
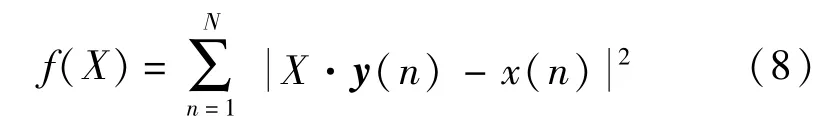
式(4)的信号进行FOA和SAA分析结果如表2所示。
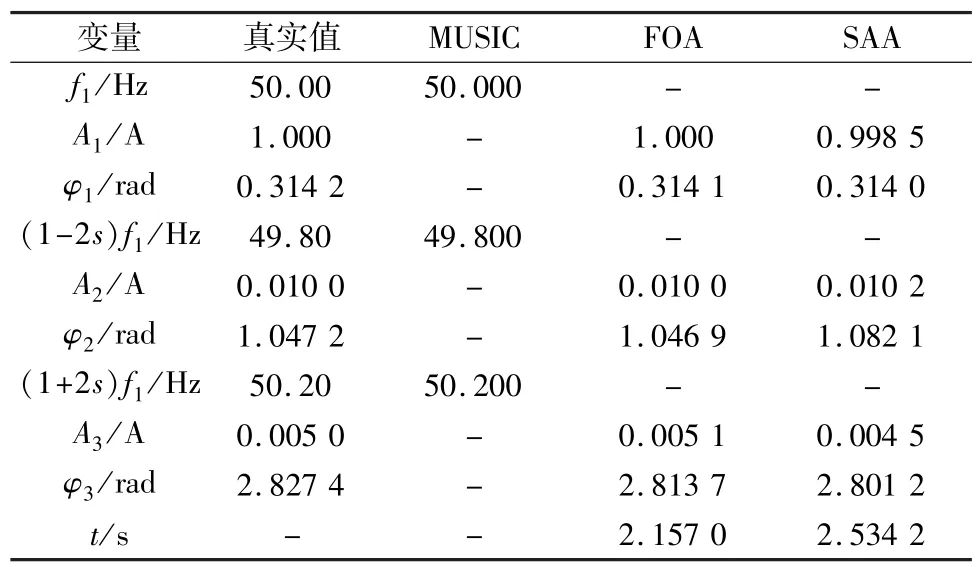
表2 FOA与SAA算法的性能比较
表2表明,在MUSIC估计频率的基础上,FOA和SAA均能计算出仅有1.5 s数据的短时采样信号各频率成分的幅值和初相角,但是FOA的计算结果明显比SAA的计算结果更接近真实值,其计算误差也在工程允许范围内。不仅如此,采用FOA进行幅值和初相角估计时,由于参数少、寻优效率高,其运算速度快于SAA,前者比后者用时缩短了近15%。
3 基于MUSIC与FOA的异步电动机转子断条故障检测方法
3.1 基本流程
1)采集A相定子电流信号,记为i(采样频率5 kHz,采样时长10 s)。从中提取一段长度1.5 s的数据,要求其比较平稳即可,记为is。
2)经带通滤波器进行滤波,用MUSIC确定is各个频率分量的频率。
3)根据频率估算结果,应用FOA确定各频率分量的幅值。
4)根据边频分量与基频分量的幅值之比确定转子断条情况。
本文采用转子齿槽谐波转差率估计技术解决MUSIC可能产生虚假频率的问题。首先在MUSIC对频率的估计结果中选出最接近供电频率的基频f1,再通过包含于定子电流中的齿槽谐波分量确定转差率s,进而便可以确定边频分量(1±2s)f1的大小。
3.2 实验结果
实验电机为一台Y132M-4型感应电机,其主要技术参数如表3所示。

表3 实验电机主要技术参数
分别对轻载1根断条、满载2根断条的故障电机进行实验。实验时,电流的采样频率和采样时间分别为5 kHz,1.5 s。A相定子电流在两种情况下的波形如图1所示。
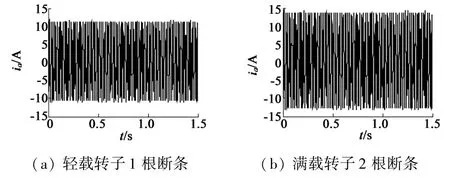
图1 定子电流信号波形
图2为两种方法下电机轻载转子1根断条的实验结果频谱图。由图2可知,采用FFT分析时,由于基频分量的泄露及过小的转差率,故障特征分量被基频分量淹没而难以辨认。当采用基于MUSIC与FOA的新方法时可以明显分辨故障特征分量。

图2 轻载转子1根断条情况下的实验结果
图3为两种方法下电机满载转子2根断条的实验结果频谱图。由图3可知,由于故障程度加剧及转差率增大,采用FFT分析时故障特征分量没被基频分量完全淹没,但是仍非常微弱,辨认困难。采用基于MUSIC与FOA相结合的方法时可以更加容易分辨故障特征分量。

图3 满载转子2根断条情况下的实验结果
表4、表5给出了两种故障情况下,采用FFT与新方法的各个频率分量参数辨识结果。由于初相角对断条严重程度的判断没有太大意义,故表中未给出。同时为了比较1.5 s数据时FFT与新方法的检测精度,在表中给出了10.0 s数据时的FFT检测结果。
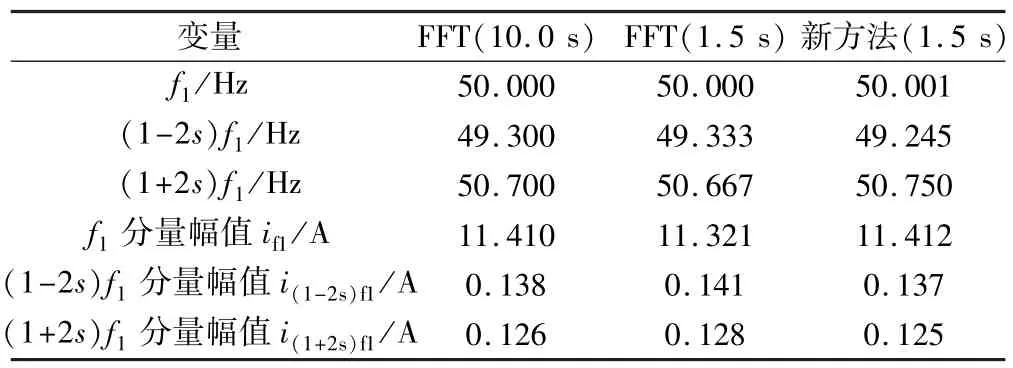
表4 轻载转子1根断条实验结果
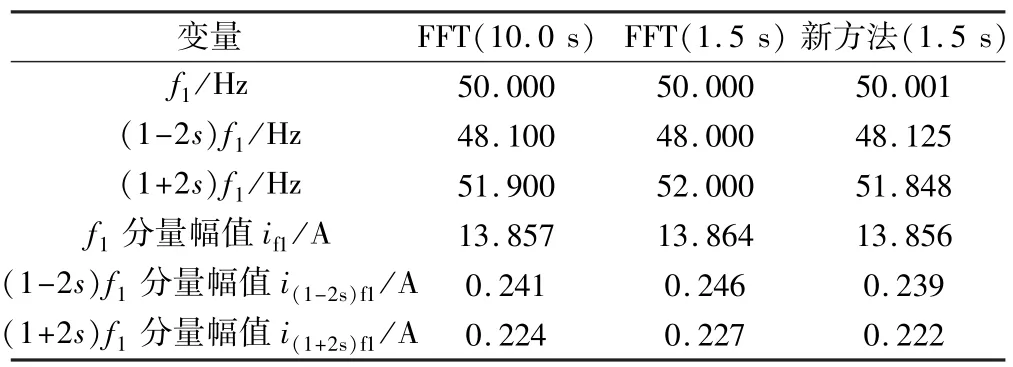
表5 满载转子2根断条实验结果
由表4、表5可知,对于短时采样信号,FFT的检测精度明显下降,然而基于MUSIC与FOA的新方法却并不受采样时间短的影响,检测性能良好,效果理想。
4 结 语
MUSIC算法是一种具有高分辨率的谱估计技术,将其用于异步电动机转子断条故障检测取得良好效果。MUSIC不仅具有较高的频率分辨力,信号不需要正周期采样,对于短时信号均有很好的性能,同时能够克服FFT中频谱泄露和栅栏效应的缺点。FOA作为一种新的群智能算法,具有精度高、参数少、耗时少的优点,能够精准计算各频率分量的幅值和相位。通过仿真和实验进一步证实了将MUSIC与FOA相结合的方法用于异步电机转子断条故障检测是有效的,提高了异步电机转子断条故障检测的准确性,且有利于实时故障的检测。
参考文献
[1] 刘振兴,尹项根,张哲,等.基于瞬时功率信号频谱分析的鼠笼式异步电动机转子故障在线诊断方法[J].中国电机工程学报,2003,23(10):148-152.
[2] 马宏忠,胡虔生,黄允凯,等.感应电机转子绕组故障仿真与实验研究[J].中国电机工程学报,2003,23(4):111-116.
[3] DELEROI W,DELEROI W.Broken bar in a squirrel-cage rotor of an induction motor[J].1984,67(3):141-149.
[4] 许伯强,孙丽玲,李和明.基于高频率分辨力谱估计技术与优化算法的异步电动机转子故障检测新方法[J].中国电机工程学报,2013,33(3):140-147.
[5] 王攀攀,史丽萍,张勇,等.采用一种混合骨干微粒群优化算法的感应电机转子断条故障诊断[J].中国电机工程学报,2012,32(30):73-81,13.
[6] 孙丽玲,许伯强,李志远.基于MUSIC与SAA的笼型异步电动机转子断条故障检测[J].电工技术学报,2012,27(12):205-212.
[7] 卜乐平,夏立.基于MUSIC算法的异步电动机转子故障检测方法[J].电机与控制应用,2005,32(5):56-59.
[8] 许伯强,孙丽玲,李和明.笼型异步电动机转子断条数目诊断新判据[J].中国电机工程学报,2009,29(6):105-101.
[9] 潘文超.果蝇最佳化演算法[M].台北:沧海书局,2011:10-12.
[10] 胡能发.演化式果蝇算法及其应用研究[J].计算机技术与发展,2013,23(7):131-133.
[11] 韩俊英,刘成忠.自适应调整参数的果蝇优化算法[J].计算机工程与应用,2014,50(7):50-55.
[12] 单单.止损策略对双随机安全第一投资组合模型的影响研究[D].重庆:重庆大学,2014.
[13] 张贤达.现代信号处理[M].北京:清华大学:2002:125-150.
[14] PAN W T.A new fruit fly optimization algorithm:Taking the financial distress model as an example[J].Knowledge-Based Systems,2012,26(2):69-74.
[15] PAN W T.Using modified fruit fly optimisation algorithm to perform the function test and case studies[J].Connection Science,2013,25(2-3):151-160.

