温度对超声波电动机起动阶段位移分辨率的影响

郑 伟,黄伟彬,罗敏峰

(福建工程学院,福州350118)

0 引 言

超声波电动机是利用逆压电效应和摩擦作用将电能转化为机械能,与传统的电磁电机相比较,表现出重量轻、低转速、输出大力矩和定位精度高等特点,在各种新兴高科技领域呈现出良好的应用前景[1-3],因此希望超声波电动机能有足够的定位精度便于精确控制。由于超声波电动机中摩擦界面的性质、压电陶瓷的压电性和定转子结构的动力学特性都与温度密切相关,关于温度对超声波电动机机械性能的影响受到广泛关注[4-6]。事实上,在机械特性变化的同时,定位精度也因位移分辨率的温度敏感性而受到显著影响。超声波电动机的定位精度高得益于断电自锁特性和良好的定子振幅可控性,使得位移分辨率可以达到很高的水平。理想条件(恒温、隔振等)下,位移分辨率可达纳米级甚至亚纳米级,对常温下超声波电动机分辨率的控制方法的研究取得了长足进步[7-10]。然而,由于压电陶瓷本身存在温升,超声波电动机运行过程中定/转子摩擦产生温升,而高位移分辨率的实现依赖于起动阶段的温度稳定性,温度对位移分辨率的影响成为超声波电动机高精度定位不可回避的问题。

本文通过对超声波电动机定子弹性体中压电材料、摩擦材料等在不同温度下进行特性分析,剖析温度对超声波电动机位移分辨率影响机理,通过试验验证影响机理,并通过前馈方法对单台超声波电动机进行控制,提高其分辨率的稳定性。

1 温度对超声波电动机分辨率影响分析

旋转型行波超声波电动机主要由定子和压电陶瓷组成的定子产生超声振动,从而驱动转子。超声波电动机的驱动元件为压电陶瓷,定子金属材料主要由铜基材料加工,在常温下温度变化对铜基材料性能的影响很小,而压电陶瓷的温度特性具有很强的非线性特性。

旋转型行波超声波电动机的定子是由定子金属体和压电陶瓷组成,通过逆压电效应工作[11]。沿着极化方向在压电陶瓷上施加激励电压V=V0sinωt,V0为电压幅值。根据逆压电效应,压电陶瓷产生变形,该变形等效为基础位移激振方式的交变变形,用于驱动超声波电动机定子。因此压电陶瓷的性能是超声波电动机定子振动的重要影响因素之一。在超声波电动机的设计中,常用的压电方程为第一类压电方程[12]:

式中:ε为应变;D是当电场强度E为常数时的电位移强度弹性柔度常数;σj为应力;En为电场强度;d是压电常数;表示σ为常数时的介电常数。式(1)是应用在不考虑温度影响下的情况,压电常数dni与环境温度成线性关系。

通过对压电陶瓷在不同的温度环境下试验[12],根据超声波电动机用压电陶瓷的特点,对常温环境下的压电方程进行修正。考虑温度对压电陶瓷的影响,得到的压电方程:

式中:d是压电常数;ΔT为温度变化量,d-为含温度影响的压电常数;是热膨胀系数;e-为含温度影响的介电系数恒定应力下的热电系数。

与式(1)相比较,式(2)中考虑了环境温度变化对压电常数的影响以及压电陶瓷在不同温度环境下热膨胀和热释电等因素。

与温度相关的物理量α与温度的函数关系可展开级数[13],即:

式中:α0为α(物理量)在参考温度T0时的值;和分别表示α(物理量)在参考温度T0时的一级、二级和三级温度系数,它们的定义:因此,α在温度T时的温度系数Tα的表达式:

温度系数物理意义:在某温度下,当温度每变化1℃时,α所产生的相对变化。从式(3)～式(5)看出,式(2)只考虑了一级温度系数[12],该式能较好地反映压电陶瓷在不同温度环境下的性能变化。文献[14]对超声波电动机用压电陶瓷的压电常数d33在不同环境温度下进行测量,其试验结果如图1所示。从图1中可以看出,在常温15℃ ～35℃的范围内,压电常数依然有小的波动。

图1 不同温度下压电常数变化

在文献[14]中,对该数据进行线性化处理,其压电方程如下:

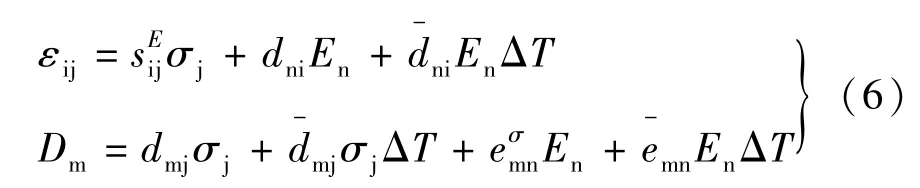
本文研究的温度范围在5℃～40℃的范围内,用比较接近试验数据的方程来描述,其中d-为考虑了温度因素的压电应变常数;其值为随着温度变化的值,因此将式(6)中修正:

式中:A为在标准测试温度下压电陶瓷压电常数。修正后的压电方程是否符合实际情况,需要通过对超声波电动机在不同本体温度下试验进行验证。本试验不涉及控制,只测试常态下温度对超声波电动机本体分辨率的影响。

2 试验设计

通过上节分析了温度对超声波电动机位移分辨率的影响因素,本节通过试验对其进行验证。

2.1 超声波电动机位移分辨率试验组成

本试验系统如图2所示,通过电机轴的反光,反算出电机转过的角度[7]。

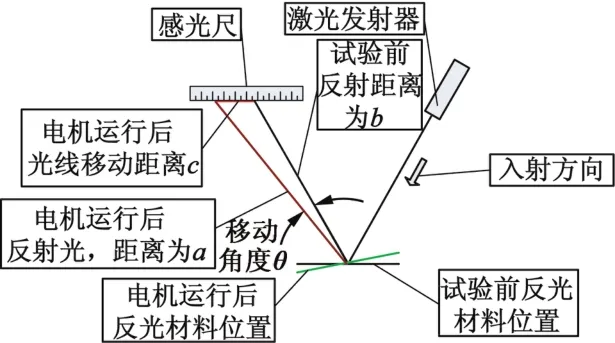
图2 超声波电动机位移分辨率试验系统

2.2 试验设计

本试验使用TRUM-60旋转型行波超声波电动机作为试验对象,单片机控制位移(型号为STC89-C52RC),单片机的P1.0为电机驱动器的启停控制,射激光光线到尺上,通过单片机控制超声波电动机运动,超声波电动机运动根据余弦定理:P1.1为正反转控制口。P1.0通过控制超声波电动机起动来实现超声波电动机运行的时间,该方法的实现是通过定时器T0中断实现的。

由于超声波电动机是通过摩擦传递运动和力,因此超声波电动机从开始运行起,本体就开始发热,直到其本体发热与环境达到热平衡后,本体温度才稳定下来不再变化。本试验用TRUM60型超声波电动机作为试验对象,从运行开始到与环境达到热平衡为试验时间,因此,对本试验首先在室温下,测量超声波电动机位置分辨率,然后将其空载运行固定间隔时间后,再测试超声波电动机的温度和位置分辨率,以观察变化规律。

3 试验结果及分析

3.1 试验过程及结果

根据2.2中的试验设计,搭建试验系统,其试验系统如图3所示。

图3 位移分辨率试验

在不同的超声波电动机本体温度下,通过单片机程序,对P1.0口输出,确定控制驱动器驱动超声波电动机运行时间,测量超声波电动机转过的角度,从而得到不同本体温度下超声波电动机的位移分辨率。

在常温下,将冷态的超声波电动机驱动器通过单片机控制超声波电动机运行100 μs,并通过式(6)计算平均值及转动角度误差,在超声波电动机运行10 min后,测量超声波电动机本体温度后,继续测试分辨率,如此重复。

该试验样本TRUM60参数:定子直径60 mm,驱动频率40kHz,额定转速120r/min,额定扭矩0.5 N·m,额定输出功率6 W,最大扭矩1.6 N·m,最大转速150 r/min。试验分两次完成,其室内环境温度分别为16℃和24℃,每15次测量作为一组数据,测试完成后,电机连续运行10 min后,继续测试15次为一组,直到电机的温度与外界环境温度达到热平衡。取典型数据进行分析,如图4所示,电机的表面温度依次为16.3℃,18.8℃,24.3℃,27.0℃,31.2℃,34.9℃(随后测量表面温度在34.3℃ ～35.4℃这个区间变化)。其中,测试点18.8℃的具体意义是在室温为16℃时,电机从16.3℃开始运行,当表面温度达到25.5℃后,在室温中降温到18.8℃后测试。

将该数据代入式(7)中,a=1.01×10-2,b1=-3.8×10-4,b2=1.2×10-5。 在该组数据中,可以简化为一阶。为了验证该趋势与压电元件在不同温度下性能变化,进行如下试验验证。

图4 不同温度下超声波电动机分辨率

3.2 试验验证

本控制方法是应用上节得到的压电陶瓷受温度影响得到的结论,为了验证起动阶段超声波电动机分辨率变化主要由压电陶瓷影响而产生的,利用试验得到式(6)中的修正数据。结合控制用单片机,通过软件设定输出不同时间长度,该时间长度是通过修正后的式(6)计算所得,用于补偿超声波电动机起动阶段的分辨率。将单片机的控制输出端接入驱动器,将单片机的P1.0口作为控制口,单片机硬件如图5所示。

图5 超声波电动机分辨率控制装置

针对本次试验用超声波电动机,超声波电动机用试验中得到的数据代入式(7)中进行控制,由于16℃ ～24.3℃阶段角度变化小(0.000 2°),因此只取从24.3℃开始验证。超声波电动机在室温下,P1.0口的输出脉冲宽度分别为130 μs持续10 min,120 μs持续 10 min,110 μs 持续 10 min,105 μs 正常工作,测量分辨率,并根据测量结果修正P1.0口输出脉冲宽度的时间,最终调整的时间脉冲宽度为143 μs,121 μs,109 μs,102 μs,最终超声波电动机的分辨率如图6所示。

图6 应用前馈控制后不同温度下超声波电动机分辨率

图6中采用与图4同比例显示,可以看出通过补偿压电陶瓷性能的变化,可以有效降低波动误差。但是同时也降低了超声波电动机的分辨率,从0.007°变化到0.012°,而且是针对本试验超声波电动机,由于超声波电动机的制造工艺和原材料很难保证完全一致,因此应用式(6)可以对超声波电动机分辨率的稳定性进行验证,但是其参数不具有通用性。从本文所提及的超声波电动机可以看出,压电陶瓷是影响其分辨率的重要因素之一,如要进一步量化,需要对压电陶瓷、粘贴工艺在不同温度下性能变化结合起来进行研究。

4 结 语

从温度与压电陶瓷性能关系的角度,对超声波电动机位移分辨率与温度的关系进行分析,并进行试验,从试验结果可以得到:(1)当需要精密驱动的情况下,超声波电动机本身运行时产生的温度变化影响超声波电动机的分辨率;(2)温度对压电陶瓷的影响能够反映到超声波电动机位移分辨率上;(3)在超声波电动机的起动阶段,如需改善分辨率,可以从考虑提高压电陶瓷的温度稳定性方面进行设计。

参考文献

[1] 赵淳生.世界超声波电动机技术的新进展[J].振动测试与诊断,2004,24(1):1-5.

[2] 芦小龙,张建辉,赵淳生.行波型旋转超声波电动机温度场分析方法[J].中国电机工程学报,2011,31(18):33-39.

[3] 潘松,菅磊,黄卫清.超声波电动机直驱的电动物镜控制方法[J].振动:测试与诊断,2016,36(4):796-800.

[4] 郭超,杨明,李世阳.基于温度反馈的超声波电动机速度控制系统[J].微特电机,2012,40(5):62-64.

[5] 王光庆,郭吉丰.行波型超声波电机的温度特性[J].中国电机工程学报,2008,28(9):98-104.

[6] 芦小龙,张建辉,赵淳生.行波型旋转超声波电动机温度场分析方法[J].中国电机工程学报,2011,31(18):33-39.

[7] 苏民伟,罗敏峰,郑伟.超声波电动机位移分辨率特性研究[J].组合机床与自动化加工技术,2016(2):9-12.

[8] XIE Yangqiu,TAN Yonghong,DONG Ruili.Nonlinear modeling and decoupling control of XY micropositioning stages with piezoelectric actuators[J].Mechatronics,IEEE/ASME Transactions,2013,18(3):821-832.

[9] 芦小龙.用于空间环境的超声波电动机的研究[D].南京:南京航空航天大学,2014.

[10] 阮玉镇,郑伟.旋转型行波超声波电动机磨损控制研究[J].微特电机,2015(1):43-45.

[11] 赵淳生.超声电机技术与应用[M].北京:科学出版社,2010.

[12] WANG D,FOTINICH Y,CARMAN G P.Influence of temperature on the electromechanical and fatigue behavior of piezoelectric ceramics[J].Journal of Applied Physics.1998,83(10):5342-5350.

[13] 张沛霖,张仲渊.压电测量[M].北京:国防工业出版社,1983.

[14] 郑伟,赵淳生.低温环境下超声波电动机定子特性[J].南京航空航天大学学报,2009,41(1):1-5.

[15] 郑伟.超声波电动机寿命及温度适应性研究[D].南京:南京航空航天大学,2008.