一种外伸梁式弹簧定子超声波电动机的设计

董迎晖,赵言安,顾雅春

(合肥工业大学,合肥230009)

0 引 言

超声波电动机是一种利用压电元件的逆压电效应、弹性体超声频域内的谐振和定、转子之间的摩擦传动实现致动输出的新型电机[1]。与传统的电磁电机相比,超声波电动机具有结构简单紧凑、响应快、控制精度高、转速低、能量密度大、无电磁干扰、无噪声污染等优点[2-3]。目前,超声波电动机已应用于航空航天、汽车工业、生物医学、精密仪器等领域[4]。

毫米量级的微型弹簧定子超声波电动机由于更为短小轻薄的结构,在微尺寸领域更具优势。微型超声波电动机按定子形状可分成三类:管式定子超声波电动机、柱式定子超声波电动机和弹簧定子超声波电动机。管式超声波电动机国外研究较多,典型的有T.Morita等[5]研制的压电薄膜管式超声波电动机;S.X.Dong等[6]研制的管式压电陶瓷超声波电动机。国内方面,朱华[7]和王天华[8]等对上述几种管式超声波电动机进行优化改进。柱式超声波电动机以国内研究为主,但是这种超声波电动机采用管式定子,结构较为复杂,进一步微小化存在较大的难度。Tadashi Moriya[9]等人于2005年提出一种用Lamb波驱动的弹簧定子超声波电动机,取一个直径为0.3 mm的不锈钢丝作转子,将另一直径为0.25 mm的不锈钢丝绕在转子上形成螺旋状的定子。该电机结构简单,尺寸微小,被应用于血管超声波扫描仪中。但此种电机需要较长的波导,占用空间,而且输出扭矩较小,能量损耗大,应用受限。为解决采用Lamb波驱动的弹簧定子超声波电动机存在的问题,我们曾提出一种采用弯曲行波驱动的弹簧定子超声波电动机,电机的结构如图1所示[10]。将两组压电陶瓷粘贴在弹簧定子的两端面上,施加电压以激发定子的两相弯振模态,利用模态叠加法将这两相弯振模态合成驱动行波。由于弹簧定子两端面是曲面,压电陶瓷的粘接不可靠,影响电机的实际工作性能。在此基础上,本文提出一种改进结构的外伸梁式弹簧定子超声波电动机,用一块外伸梁跟弹簧定子固连,将压电陶瓷固定在外伸梁上,解决了压电陶瓷粘接不可靠的问题。

图1 弹簧定子超声波电动机结构示意图

1 电机的基本结构和驱动原理

超声波电动机的基本结构示意图如图2所示。定子由压电陶瓷、外伸梁、连接板和弹簧4部分组成。转子、弹簧定子、外伸梁与连接板的材料均为不锈钢,其中弹簧截面为正方形;外伸梁结构通过两片连接板焊接在弹簧左右端的螺圈上;在外伸梁的3个外表面上粘贴3片压电陶瓷,粘贴位置如图2所示。

图2 外伸梁式弹簧定子超声波电动机结构示意图

本文所提出的外伸梁式弹簧定子超声波电动机采用模态叠加法产生行波,压电陶瓷的极化方向如图3所示。为使超声波电动机能够安全的使用,故将3片压电陶瓷的内表面接地;上方压电陶瓷沿Y轴正向极化,并在压电陶瓷外表面施加正弦激励电压,以激发弹簧沿Y轴方向的一阶弯曲振动;左右两块压电陶瓷沿X轴正向极化,并在压电陶瓷外表面施加余弦激励电压,以激发弹簧沿X轴方向的一阶弯曲振动。这两相一阶弯曲振动各在时间上相差π/2相位、空间上相互垂直,由模态叠加可知,当这两相一阶弯曲振动被同时激发出来时,在弹簧定子中就会叠加合成为一列行波,使定子内表面的各个质点做椭圆运动。

图3 压电陶瓷的极化方式

2 定子结构参数的优化设计

由超声波电动机的驱动原理可知,让定子产生同频同型的两相弯曲振动模态是决定定子内表面各质点能否做椭圆运动的关键。但因定子的结构并不是对称的,所以这两相一阶弯曲振动模态也不是完全相同,如果这两相一阶弯曲振动频率差异较大就会使超声波电动机的输出功率发生波动,从而影响电机的输出性能,所以必须对弹簧定子的各个结构做相应的优化设计,以达到电机的X,Y相的特征频率相近的目的。取弹簧定子的中径(d)、螺距(t)、边长(b)和外伸梁的长(l)、宽(w)、高(h)6个结构参数为优化变量,对弹簧定子的两相一阶弯曲频率进行优化,使频率及其差值满足要求。

利用标准正交表L8(27)设计正交试验,结合有限元软件ANSYS,找出两相一阶弯振频率及其差值与各设计变量之间的关系。试验结果如表1所示。

表1 弹簧定子设计变量正交试验

对正交试验的结果数据采用多元线性回归计算处理。

以x向弯振频率为指标y1,通过计算回归方程如下:

由式(1)可以看出,影响x向弯振频率的主要因素是弹簧截面边长b,其次是内径d与外伸梁宽w。

以y向弯振频率为指标y2,回归方程如下:

由式(12)可以看出,影响y向弯振频率的主要因素是弹簧截面边长b,其次是内径d与螺距t。

通过多元线性回归分析可知:弹簧的边长b、中径d和螺距t对两相弯振频率的影响最大,因此在对弹簧定子各个结构进行优化时优先考虑弹簧的这3个参数的调整。弹簧的边长b、中径d和螺距t3个参数对频率的影响趋势如图4所示。

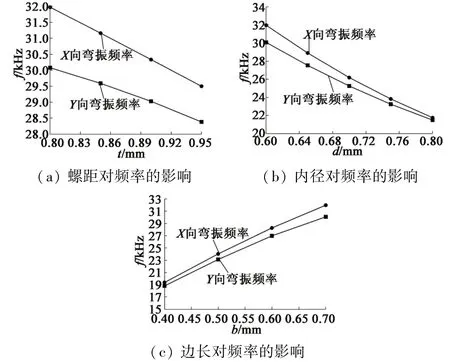
图4 弹簧参数对频率的影响图

综合以上弹簧定子参数对频率的影响趋势与弹簧定子自身几何尺寸的约束,利用有限元分析软件ANSYS对弹簧定子各个结构参数进行调整,找到一组综合性能较好的弹簧定子结构参数的组合,具体尺寸如表2所示。由表2可以看出,优化后,弹簧定子x,y方向的一阶弯曲振动模态的固有频率分别增大至22 396 Hz和22 368 Hz,而频率差仅为28 Hz,故优化效果明显。

表2 弹簧定子尺寸优化结果

3 优化后定子运动特性分析

根据表2中的优化后的弹簧定子各个结构参数重新对定子进行建模,并对定子进行模态分析。分析结果如图5所示,图5分别表示的是弹簧定子的X,Y相一阶弯振模态,即定子的工作模态。由超声波电动机工作原理可知,只要弹簧定子中激励出两相一阶弯曲振动,则定子内表面上与转子相接触的各个质点就能形成椭圆运动,由此便可通过摩擦力来驱动定子转动。

图5 弹簧定子两相弯振模态图

对弹簧定子进行谐响应分析,选取弹簧左端面一个节点作为定子谐响应的分析点,如图6所示可选取图中的P4点,绘制该节点的位移随频率响应曲线,如图7所示。

分析可知,由于弹簧结构并不是完全对称的,导致Y向一阶弯曲振动的振幅大于X向振幅,但在频率为22.37 kHz左右处,定子的两相振幅基本相同,振幅约1.6 μm,达到驱动转子的要求。

图6 定子节点选取示意图

图7 优化后定子的位移响应曲线

对定子进行瞬态动力学的分析,绘制图6中的6个节点的运动轨迹,如图8所示。从图8中可以看出,6个节点的运动方向均为逆时针,从而确保弹簧定子内表面上各个质点对转子驱动力方向的一致性。但由于弹簧定子的结构存在不对称性,椭圆轨迹相对于正椭圆有一定程度的倾斜。其中,P1和P2节点处的椭圆运动发生4处畸变,对转子的驱动效果有所影响;其余4个节点的椭圆轨迹相比于P1和P2节点更加光滑,并且振幅更大,对转子的驱动效果好。对行波在定子中的传播路径分析可知,因连接板与定子和外伸梁与连接板均是独立结构彼此连接在一起,行波传播至这两个部位时会产生一定突变,并会增大这两个部位的局部刚度,因此更靠近定子内表面处的4个节点的行波传播质量更好,振动幅度也更大,椭圆运动轨迹也更加光滑。

图8 定子的椭圆运动轨迹

总结:虽然行波在传播过程中由于定子结构的不规则产生了一定的突变,导致外伸梁附近的一些节点椭圆运动轨迹发生内凹,但定子内表面处的节点椭圆运动轨迹都比较光滑,X与Y向振动的振幅也能达到2 μm,能够满足驱动要求。

4 结 语

本文在此前研究的基础上提出了一种改进结构的弹簧定子超声波电动机,通过外伸梁结构来解决压电陶瓷与定子粘接不可靠的问题。设计了该电机的驱动方式,并从理论上分析了驱动面质点有效椭圆运动的存在性;采用正交试验和ANSYS软件对定子的结构参数进行优化设计,通过对比,优化后弹簧定子的动力学特性得到较大的提高。

参考文献

[1] 赵淳生.超声电机技术与应用[M].北京:科学出版社,2007:1-25.

[2] 赵淳生.21世纪超声电机技术展望[J].振动、测试与诊断,2000,20(1):7-11.

[3] 陈超,任金华,石明友,等.旋转行波超声电机的冲击动力学模拟及实验[J].振动、测试与诊断,2014,34(1):8-14.

[4] 赵淳生.世界超声电机技术的新进展[J].振动、测试与诊断,2004,24(1):1-5.

[5] MORITA T,KUROSAWA M,HIGUCHI T.An ultrasonic motor using a bending cylindrical transducer based on PZT thin film[J].Sensors and actuators,1995,50(1-2):75-80.

[6] DONG S X,LIM S P,LEE K H,et al.Piezoelectric ultrasonic micromotor with 1.5mm diameter[J].IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control,2003,50(4):361-367.

[7] 朱华,陈超,赵淳生.一种微型柱体超声电机的研究[J].中国电机工程学报,2006,26(12):128-133.

[8] 王天华,张辉.1mm管式悬臂梁结构微型超声马达研究[J].南京大学学报学报,2007,43(4):419-425.

[9] MORIYA T,AKANO Y,FURUKAWA Y,NAKAJIMA A.Development of a miniature ultrasonic motor using a helical coil as a stator[C]//IEEE Ultrasonic Symposium,2005:1546-1549.

[10] 董迎晖,顾雅春,汤开元,等.采用弯曲振动模态的弹簧定子超声电机[J].振动、测试与诊断,2013,33(157):13-16.