基于带载能力最大化的PMSM单电流调节器弱磁控制

孙鹤旭,刘 杰,董 砚,荆 锴

(1.河北工业大学,天津300130;2.河北科技大学,石家庄050018)

0 引 言

永磁同步电机(以下简称PMSM)以其高功率密度、高功率因数、结构简单等一系列优点,广泛应用于家用电器、交通运输、航空航天以及机床、机器人等领域[1]。近年来电动汽车行业蓬勃发展,为适应电动汽车的高速运行,电机必须具备良好的弱磁调速性能,因此本文对PMSM弱磁调速控制进行了研究。

针对PMSM弱磁控制,学者们做了大量研究,文献[2]从改善电机结构的角度入手,通过重新设计电机结构对PMSM弱磁进行了分析。从控制策略的角度,传统弱磁电流轨迹可通过公式法[3]、查表法[4]、梯度下降法[5]等控制方法规划获得,但上述方法计算过程较为复杂,实际工程实现困难。文献[6-7]提出一种基于电压外环的反馈补偿弱磁控制算法,将电压偏差量作为弱磁控制的输入量,易于实现。上述各种方法均含有两个电流调节器,交直轴电流耦合作用会随着电机转速的上升而增强,这种耦合会导致电机高速运行时控制效果变差,严重时可能导致系统失控。文献[8]提出一种单电流调节器弱磁控制,仅控制直轴电流分量,从而解决了双电流控制时交直轴电流耦合的问题,动态响应快,易于实现。但是该文献中没有具体分析能够仅利用直轴电流调节器进行弱磁控制的原因,且母线电压和带载能力没有充分利用。

针对上述问题,本文在文献[8]基础上,根据内嵌式PMSM数学模型从理论上分析了其单电流调节器弱磁控制的可行性,并针对电机单电流调节器弱磁控制带载能力弱的问题,提出了一种全新的交轴电压给定方法,提高单电流调节器弱磁控制的转矩输出能力,改善单电流调节器弱磁控制性能,搭建了仿真模型,并根据仿真模型进行了实验验证。

1 PMSM单电流调节器弱磁控制可行性分析

传统弱磁控制交直轴电流环各有一个电流调节器进行调节。单电流调节器弱磁控制在传统控制基础上去掉了其中一个电流调节器,取而代之的是直接给定其电压控制量。

若去掉交轴电流调节器,交轴电压直接给定为定值uq=uFWC,此时在同步旋转坐标系下,PMSM稳态电压方程:

式中:id,iq为定子电流交直轴分量;Ld,Lq为电机交直轴电感;ωr为电机的电角速度;ψf为永磁体磁链。

电磁转矩方程:

式中:p为电机极对数。将式(2)变形可得:

式(4)称为交直轴电流耦合方程。可以看出,当q轴电压给一个恒定值时,iq,id呈线性关系,通过控制一个电流变量id即可控制另一电流变量iq。在小变量范围内进行,由式(4)可得:

由式(1)可得:

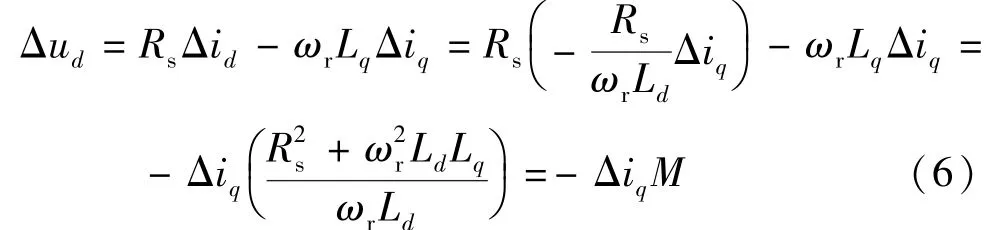
式中由式(3)可得:

结合式(5)～式(7)可知,id一个变量即可控制iq从而控制ud最终控制转矩输出。

若将直轴电压给定为定值ud=uFWC,同理可以分析得:

由式(8)可以看出,给定直轴电压的情况下,iq,id也呈线性关系,也可以通过控制其中一个电流变量从而控制另一电流变量。但不同于交轴电压给定的是,此时iq,id之间的比例系数为正值,当负载变大时,id会随之正向增大,导致弱磁工作范围非常有限。以电动状态运行的内置式PMSM为例,如图1所示,假设电机当前处在稳定的弱磁工作点P,当负载增加时,即Δiq>0,根据式(9),Δid也要相应正向增加,这将导致电机的工作点向右上方向移动,最终只能落在电压极限圆上的Q1点。可以看出,这段弱磁工作范围非常有限,且最终不能满足负载转矩要求,所以定直轴电压方法不适用于弱磁控制。但若是在固定交轴电压的情况下,负载增加时,根据式(5),Δid要反向增加,即电机的工作点向左上方移动,最终能稳定在满足负载转矩的Q2点,该点仍处在电压电流极限圆内的有效工作区域,并且该方向上还有更宽的弱磁工作区域。

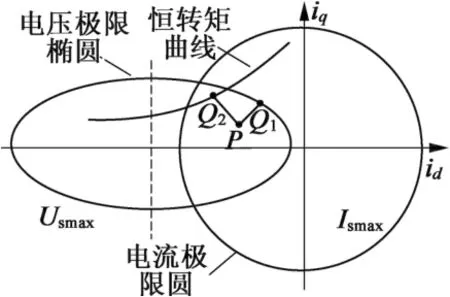
图1 弱磁工作点随负载变化示意图

基于以上分析可知,定交轴电压的单电流调节器弱磁控制在PMSM上是可行的。它不仅能够消除传统双电流调节器高速时因交直轴电流耦合而带来的调速性能差、甚至失控等问题,而且控制和实现更为简单。

2 PMSM单电流调节器弱磁优化控制

由上节分析可知,通过交直轴电流之间的耦合关系进行单电流弱磁控制,控制框图如图2所示,直轴电压指令由转速环和电流环调节获得,交轴电压直接给定。交轴电压如何给定是单电流弱磁控制中的一个重要问题,它对电机的电压利用率、运行效率和带载能力都有较大影响。目前主要有定交轴电压给定和变交轴电压给定两种方法。

图2 单电流调节器弱磁控制框图

2.1 定交轴电压单电流弱磁控制

当交轴电压uFWC为定值,转速为ω1时,如图3所示,直线EF为交直轴电流耦合方程式(4)所对应的曲线。 其中 E(-ψf/Ld+uFWC/ωrLd,0),F(-ψf/Ld,uFWC/Rs)。由坐标值可以看出,当交轴电压为固定

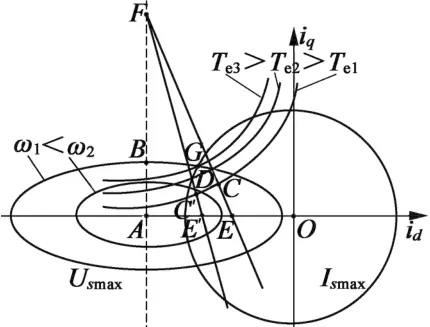
图3 定交轴电压弱磁控制电流轨迹

值时,F点位置将固定不变,E点位置将随着转速上升而左移。式(3)与式(4)的交点为PMSM的稳态工作点。当输出转矩为Te1时,稳态工作点为C点。保持转速ω1不变,当负载增加时,工作点将由C点向D点移动并停留在D点,此时转矩输出为Te2,继续加载,目标工作点将落在电压极限椭圆外而无法跟随。Te2为定交轴电压弱磁控制PMSM的最大输出转矩,其小于电机两极限圆交点处G所对应的系统最大转矩输出能力Te3。电机的带载能力没有得到充分应用。当转矩为Te1恒定不变,转速由ω1上升到ω2时,电机的稳态工作点由C点移动到C′点。但无论是C点还是C′点,都在电压和电流极限圆内,电压和带载能力都没有得到充分发挥和利用。

2.2 以带载能力最大化为目标的变交轴电压单电流弱磁控制

无论如何选择uFWC,定交轴电压的方法都不能同时兼顾电压利用率、带载能力和电机运行效率。为了改善这一问题,文献[8]提出变交轴电压给定策略,根据电机带载工况来实时改变交轴电压的给定值,给定原则为负载越小给定交轴电压越大。方程式如下:

式中:h的值与电压波动有关,一般取值范围为0.8～1。该方法缓和了电压利用率、带载能力和电机运行效率之间的矛盾关系,且着重考虑了电机的运行效率。但是电压利用率和电机带载能力并没有得到完全应用。

图4 变交轴电压弱磁控制电流轨迹

本文主要考虑提高电机的带载能力,给出一种新的变交轴电压给定方法,如图4所示。G点为电压极限圆和电流极限圆的交点,其电压利用率和带载能力都最大,为最优工作点。电压电流约束方程如下:

式中:Ismax,Usmax分别为电机定子电流和端电压极限值。求解上式可得交点G点的坐标值:

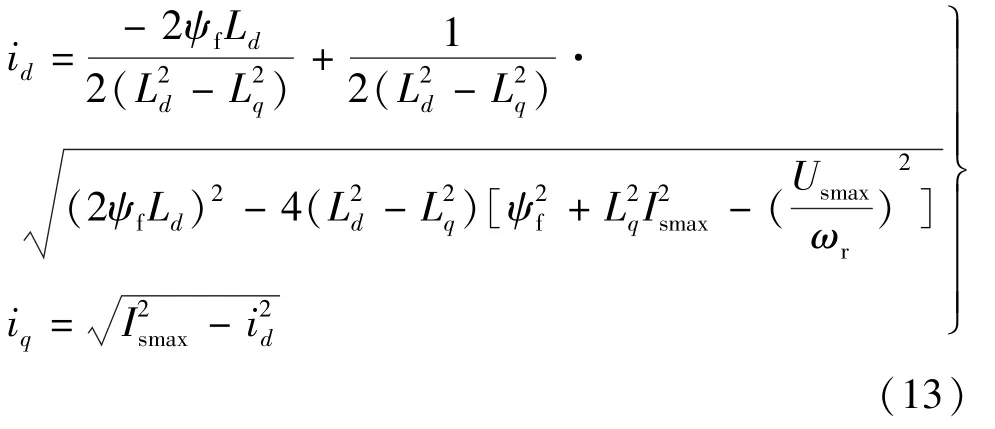
将G点坐标值代入直线EF的方程,高速时反电势很大,忽略定子电阻,可求得此时交轴电压给定值:

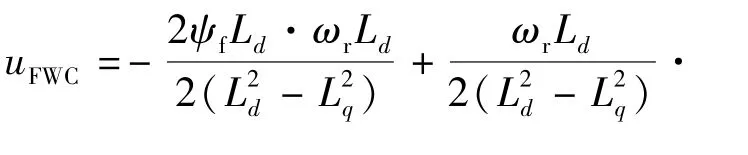
式中:除转速外其余量均为常值,通过反馈转速,实时改变uFWC,让电流耦合曲线EF穿过最优工作点G点。电机最大输出转矩可达到电压电流极限限制下的最大值,弱磁控制时系统的带载能力可得到最大发挥。

当电机转速为ω1恒定不变,负载转矩从0逐渐增加至最大时,电机的稳态工作点将从E点沿着直线EF向G点移动。当工作点落在G点时,此时弱磁控制的带载能力达到最大为Te4,这也是转速为ω1时,电压电流极限限制下系统的最大输出转矩。当负载转矩为Te6恒定不变,转速由ω1上升到ω2时,电流耦合曲线随着交轴电压的改变向曲线方向移动,稳态工作点由M点移动到点,最优工作点由G点沿着电流极限圆移动到点,此时系统能够输出的最大转矩为点对应的Te5。

由分析可知,按上述变交轴电压给定控制策略,电机输出转矩能够达到电压电流极限限制下的最大值,电机的带载能力能够得到充分发挥利用。系统的整体控制框图如图5所示,基速以下采用最大转矩电流比(以下简称MTPA)控制,基速以上采用本文单电流弱磁控制,交轴电压根据式(14)给定。

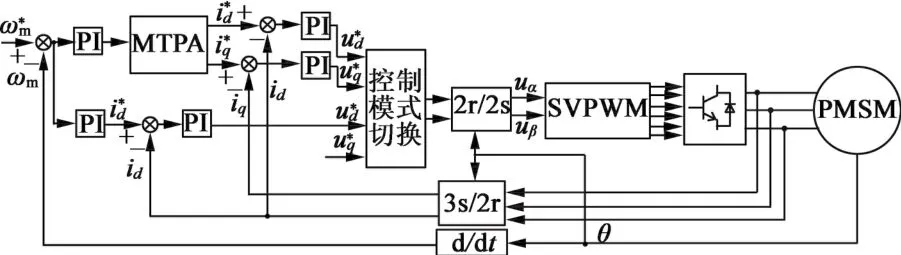
图5 系统控制框图

3 仿真分析与实验验证

3.1 仿真结果及分析

基于以上分析,搭建了PMSM系统仿真模型,电机主要参数如表1所示。

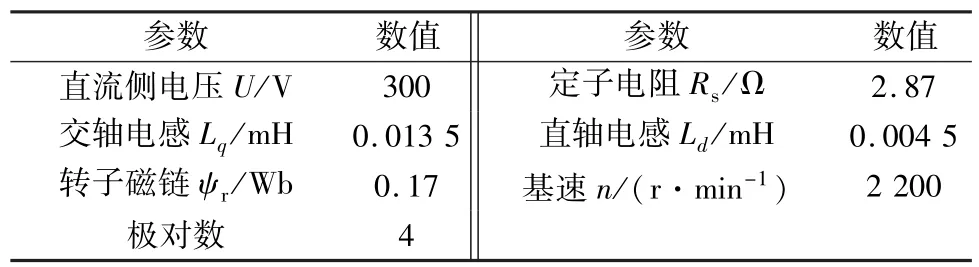
表1 电机参数

为了验证整个控制系统运行的可靠性,空载状态下给定了一个基速上下完整的转速曲线,在0～0.5 s时,给定转速为2 000 r/min,此时系统为MTPA控制;0.5～1 s时,给定转速为5 000 r/min,系统运行在弱磁控制区;1～1.5 s时给定转速回到2 000 r/min,系统又切回MTPA控制。转速响应曲线如图6(a)所示,仿真结果表明电机能很好地跟随给定转速,且转折速度2 200 r/min处电机在两种控制方式之间切换平稳。图6(b)为转矩响应曲线,系统以最大转矩电流比起动,起动瞬间会有一个大的转矩输出,但会快速稳定下来,0.5 s电机升速时会产生大的正向转矩,1 s时电机降速会产生一个大负向转矩。其余时间输出转矩都为0,转矩脉动较小。图6(c)为d轴弱磁电流变化曲线,电机起动后d轴电流快速稳定在-5 A,0.51 s电机进入弱磁控制,弱磁电流id迅速反向增大,最终稳定在-22 A;1.09 s之后系统切回MTPA控制。id恢复到-5 A,整个电流变化趋势与理论相符。图6(d)为整个过程中交轴电压uq的变化曲线,0.51～1.09 s间交轴电压的给定方法为本文提出的变交轴电压给定方法。仿真结果表明本文所提控制方法系统可平稳有效运行。

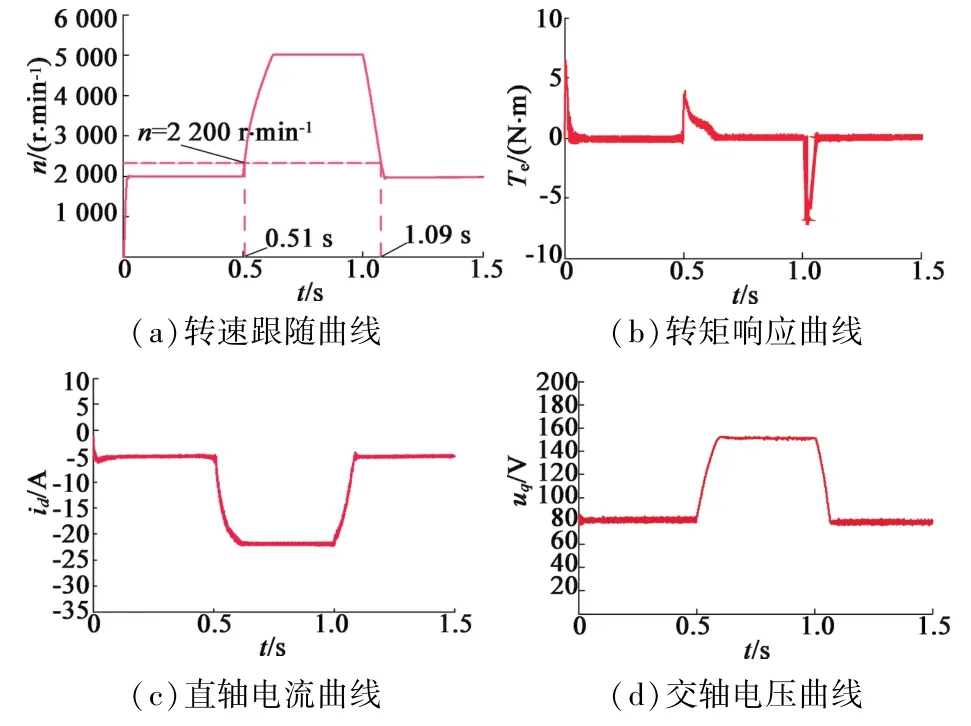
图6 转速与转矩仿真曲线

为观测电机弱磁工作点随负载和转速的变化曲线,将交直轴仿真电流绘制在id,iq坐标平面上。起始状态为转速4 000 r/min,负载转矩1 N·m的稳定工作状态,此时工作点为图7中A(A′)点,保持转速不变,当负载转矩以3 N·m/s的加速度增加,仿真结果如图7(a)所示,电流轨迹沿着电流耦合曲线从A点向B点移动,运动轨迹符合理论分析。当负载转矩不变,给定转速由4 000 r/min上升到6 000 r/min时,如图7(b)所示,电流轨迹沿着恒转矩曲线由点向C点移动。上述仿真结果显示电流运行轨迹和本文理论分析几乎一致。

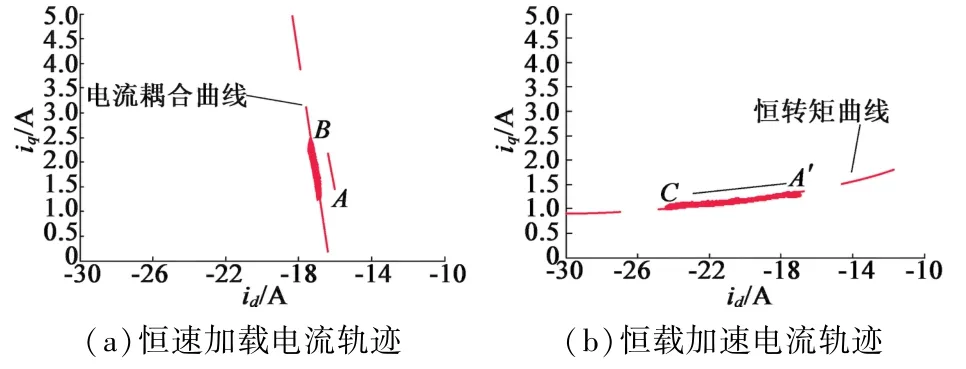
图7 电流轨迹仿真曲线

为了对比本文改进的变交轴电压弱磁控制与传统的定交轴电压弱磁控制的转矩输出能力,分别对两种控制策略进行了恒速加载仿真。仿真结果如图8所示,给定转速为恒定5 000 r/min,0～0.5 s时电机空载。待电机转速稳定之后,从0.5 s开始负载转矩以5 N·m/s的变化率恒速加载。图8(a)为本文变交轴电压控制下电机的转速和转矩波形。可以看出在1.81 s时转速由稳定的5 000 r/min开始下滑,此时负载转矩已经超过转速为5 000 r/min时系统的最大输出转矩能力,由转矩曲线可看出此时的最大输出转矩为6.55 N·m。继续加载,电机的输出转矩无法平衡负载转矩,转速将继续下降,电压极限椭圆会相应变大,输出转矩会随着转速下降仍有缓慢上升,但此时的输出转矩已不是5 000 r/min时对应的输出转矩。图8(b)为定交轴电压控制下电机的转速和转矩波形。为了更全面的对比,交轴电压在0.5 s,1 s,1.5 s时分别给定为150 V,100 V,50 V。相应时刻转速和转矩会有波动。在1.38 s时转速由5 000 r/min开始下滑,此时对应的最大输出转矩仅为4.4 N·m。对比仿真结果可明显看出,本文所提出的变交轴电压控制方法有效提高了单电流调节器弱磁控制的最大转矩输出能力。

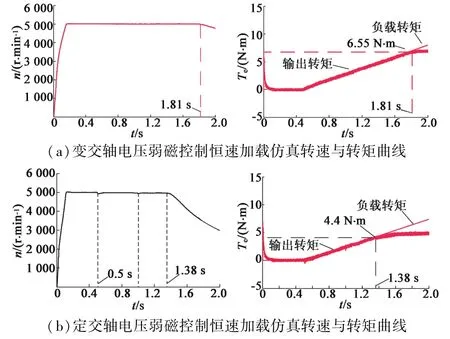
图8 恒速加载仿真曲线对比

3.2 实验结果及分析

根据仿真模型搭建了实验平台。平台主要包括调压器、两台控制器、两台内置式PMSM,其中一台为实验电机,另一台充当负载。控制板采用TI公司的TMS320F28335为核心控制芯片,功率部分主要包括三相逆变模块以及一系列检测电路。进行恒速加载实验,电机空载起动,转速稳定在目标转速5 000 r/min处,从0.5 s起负载转矩以5 N·m/s恒速加载,观测电机的转速波形。如图9(a),使用本文改进的变交轴控制策略时,1.72 s时刻负载转矩超出系统最大带载能力,转速由稳定状态开始下滑,此时刻对应系统的最大输出转矩为6.1 N·m。图9(b)为使用传统定交轴控制策略,可以看到电机转速从1.28 s时刻即开始快速下滑,对应系统的最大输出转矩仅为3.9 N·m。由于实际存在摩擦等因素,实验波形与仿真曲线存在细微差别,但实验结果依然证明了本文改进的弱磁控制策略能有效提高系统的带载能力,改善系统的控制性能。

图9 不同控制策略下恒速加载实验转速波形

4 结 语

本文从理论上分析了PMSM单电流调节器弱磁调速控制的可行性,并对交轴电压的给定进行了改进,有效提高了单电流调节器弱磁控制的最大带载能力,改善了单电流弱磁控制性能。构建了PMSM单电流调节器弱磁控制系统,取得了较好的调速效果,简单新颖,易于实现。仿真和实验都证明了本文所提方法的正确性,为电动汽车用PMSM弱磁调速提供了理论参考。

参考文献

[1] 唐朝晖,丁强,喻寿益,等.内埋式永磁同步电机的弱磁控制策略[J].电机与控制学报,2010,14(5):68-72.

[2] 张开明,钱东波,陈杰.永磁同步电动机弱磁控制的设计[J].微特电机,2009,37(6):42-45.

[3] MORIMOTO S,SANADA M,TAKEDA Y.Wide-speed operation of interior permanent magnet synchronous motors with high-performance current regulator[J].IEEE Transactions on Industry Applications,1994,30(4):920-926.

[4] LENKE R,DONCKER R,Mu Shin K,et al.Field weakening control of interior permanent magnetmachine using improved current interpolation technique[C]//Power Electronics Specialists Conference.Jelu,Korea,2006:1-5.

[5] 盛义发,喻寿益,桂卫华,等.轨道车辆用永磁同步电机系统弱磁控制策略[J].中国电机工程学报,2010,30(9):74-79.

[6] KIM J M,SUL S K.Speed control of interior permanent magnet synchronous motor-drive for the flux weakening operation[J].IEEE Transactions on Industry Applications,1997,33(4):43-48.

[7] PAICU C,TUTELEA L,ANDREESCU G,et al.Wide speed range sensorless control of PM-RSM via “active flux model” [C]//IEEE Energy Conversion Congress and Exposition.San Joe,CA,U-nited states,2009:3822-3829.

[8] SONG C,XU L,ZHANG Z.Efficiency-optimized fluxweakening control of PMSM incorporating speed regulation[C]//Power Electronics Specialists Conference.Orlando,FL,United states,2007:1627-1633.