网格曲面模型及样条曲面模型的样条实体构建的研究综述

王会颖,章义刚,李怀英

(1.安徽财贸职业学院 雪岩贸易学院，合肥 230601；2.合肥学院 建筑工程系，合肥 230601；3 .合肥工业大学 过程优化与智能决策教育部重点实验室,合肥 230009)

网格曲面模型及样条曲面模型的样条实体构建的研究综述

王会颖1,章义刚2,李怀英3

(1.安徽财贸职业学院 雪岩贸易学院，合肥 230601；2.合肥学院 建筑工程系，合肥 230601；3 .合肥工业大学 过程优化与智能决策教育部重点实验室,合肥 230009)

等几何分析的研究极大地促进了CAD、CAE的无缝结合，而如何构建样条实体模型成为制约等几何分析发展和应用推广的关键瓶颈。从等几何计算的视角出发，介绍NURBS和T样条基础理论，着重介绍了NURBS、B样条和T样条实体建模的研究进展，并分析了各种构建方法的优点和存在的不足。最后，对未来需要进一步深入研究的关键问题进行了分析和探讨。

等几何分析；NURBS样条；B样条；T样条；样条实体建模

0 引 言

计算机辅助工程(Computer Aided Engineering，CAE)中模型的表示常用多边形网格法，而计算机辅助设计(Computer Aided Design，CAD)中常用NURBS(Non- uniform Rational B- spline)样条模型表示，CAE与CAD之间存在着不兼容和模型转换问题，以及由此产生的精度降低和时间耗费等问题已经困扰了工业界数十年，严重影响工业界高精度模型和高效率计算的发展。

2005年，Hughes等提出了等几何分析(Isogeometric Analysis, IGA)，为CAD和CAE的无缝结合带来了曙光。[1]等几何分析直接将CAD中设计出的样条模型作为分析模型，节省了模型转换中耗费的大量时间，也极大地提高了计算精度。并且在传统有限元分析中，如果初次网格划分后得到的计算精度达不到设计要求，必须对该有限元模型进行重新网格划分，而在等几何分析中，则可以直接基于原有网格划分的结果对模型进行局部细化，简化了繁琐的网格划分步骤。但等几何分析的模型需要由样条实体构建，要想推进CAD和CAE的无缝融合，必须建立可用于计算分析的样条实体模型[2-3]，构建一种高效且便捷的生成样条实体的计算方法迫在眉睫。

传统的CAD模型中，实体模型常用的表示方法是边界表示法(Boundary Representation, B- rep)，使用边界曲面来表示实体，但实体内部的体积数据仍包含很多重要信息，如材料性能、密度等，[2]而且边界曲面模型无法直接用于分析。在IGA中，分析模型需要由样条实体构建[3]，所以如何将边界曲面模型转变为三变量参数样条实体模型对于等几何分析发展具有重大意义[1-2]。

目前，样条实体构建的研究仍处在初级阶段，虽然有一些开创性的成果，但使用的模型都是拥有简单拓扑结构的几何模型，由任意复杂几何模型或裁剪模型构建样条实体的方法仍未出现，现有构建算法也存在很多不完善的地方，这也是制约等几何分析发展和推广应用的关键瓶颈。本文从网格曲面模型和样条曲面模型出发，介绍了NURBS和T样条的基础理论，着重介绍了NURBS实体、B样条实体、T样条实体构建方法的研究进展并分析了其优点和不足，最后对进一步深入研究的热点问题进行了探讨。

1 B样条和T样条基础理论

1.1 NURBS、B样条实体

非均匀有理B样条(NURBS)统一了二次曲面和自由曲线曲面的表达形式，具有一套高效、快速、稳定的数值算法。NURBS有很好的数学性质，如仿射不变性，变差减缩性，凸包性等，也有很好的几何造型优势。但NURBS也存在缺陷：第一，多张NURBS曲面拼接时容易产生间隙和重叠；第二，NURBS的矩形拓扑结构使得细分时引入大量控制顶点，增大了计算量且不便于模型细化设计。[4]三变量B样条实体数学表达式如(1)式。其中，Pi,j,k,i=0,1,…,m,j=0,1,…,n,k=0,1,…,l是u,v,w方向上的控制点。Ni,p(u),Nj,p(v),Nk,r(w)是u,v,w方向上的B样条基函数。B样条实体也可被分解成Bezier体以便后续等几何分析，Bezier体可表示为(2)式，其中，Pi,j,k是控制点。Bi,p(u),Bj,q(v),Bi,r(w)是u,v,w方向上的Bernstein基函数。

(1)

(2)

1.2 T样条、T样条实体和雅克比行列式

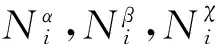
T样条实体的雅克比行列式如(4)式。 雅克比行列式值的正负是判断T样条实体是否适合于分析的重要依据。如果J为正值，则构建的T样条实体适合于等几何分析。如果J为负值，则几何模型可能存在自交和重叠的部分，不能用于等几何分析。

(3)

2 NURBS实体、B样条实体、T样条实体构建方法

2.1 T样条实体的构建

T样条提供了一种新型的几何造型技术，解决了NURBS在局部细化和拼接方面的不足。而边界曲面模型只有在经过样条实体参数化之后才能用于等几何分析，所以构建基于网格曲面模型和样条曲面模型的T样条实体尤为重要。

由于T样条及T样条实体构建的复杂性，自2003年Seder和郑建民提出T样条理论，经历了很长一段时间的研究后，2011年才出现第一篇构建T样条实体的文献。[5]随后的3年中，T样条实体的研究迎来了新高潮。2012年，张永杰和王文艳等人提出更加标准和完整的构建T样条实体的方法，[2]成为T样条实体建模发展的里程碑。随后，文献[2-7] 在上述研究的基础上，将输入模型拓宽至任意复杂边界曲面模型，并提出由T样条曲面构建T样条实体方法，但目前T样条实体构建研究的输入模型都是拥有简单拓扑结构的几何模型。

2011年，文献[6]提出通过自适应四面体网格化和网格重构光顺技术，由网格边界模型构建T样条参数化实体的方法，该方法流程如图1。该文章首次提出相对完整的由边界曲面“实体”来构建三变量T样条实体的方法。该方法关键是对边界曲面“实体”进行参数化，如图2，随后在参数化立方体单元上构建T网格，并由T网格计算生成三变量T样条实体。但该方法也存在不足：(1)T样条实体内部存在奇点，其雅克比行列式值为负值，不便于等几何分析。(2)输入的“实体”表面为零亏格，当亏格数大于零时该方法不一定适用。(3)构建的T样条实体的边界表面的连续性在参数立方体的8个角节点和12条边上为C0。

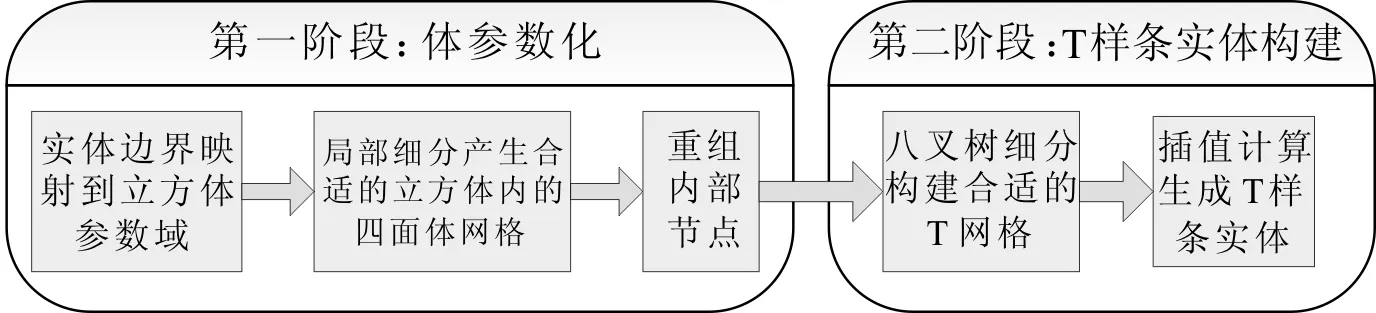
图1 文献[6]构建T样条实体方法。

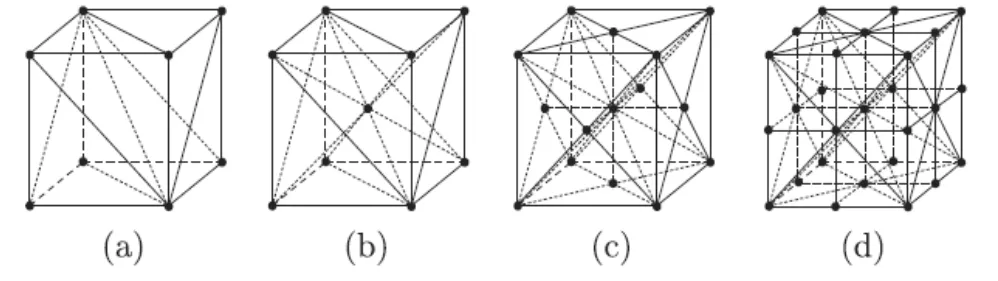
图2 文献[6]细分算法及参数化过程

随后，文献[2]提出了由零亏格边界曲面三角网格表示向T样条实体转化的方法，如图3。该文章使用映射法和八叉树细分方法将网格边界模型转化为实体T样条模型，并保证了边界曲面除边角节点外均为C2连续的特性。其中，由八叉树细分可以得到初始T网格，但此初始T网格的部分节点存在负雅克比行列式值，且边界处不具有良好的性质。该文章通过边界加层方法来提高T网格的质量和T样条实体表面的连续性。之后，通过文献[4]提出的模板化技术处理参数立方体中的奇异节点和偏奇异节点，保证T网格是无缝隙的。经过此步骤后，初始T网格转变成有效的T网格，可作为T样条实体构建的基础。随后，通过计算T网格中的节点矢量和节点基函数，构建T样条实体，并通过Beizer因子提取，将T样条实体用于等几何分析(案例如图4)。

图3 文献[2]构建T样条实体方法

图4 文献[2]由边界曲面构建T样条实体和Beizer因子提取实例

相比于之前T样条实体构建的文献，该文章提出了较为完整的T样条实体构建的方法，构建的T网格中不含有负值的雅克比行列式且保证了T样条实体的边界曲面除去边角节点外均为C2连续的性质。但该方法也存在一些缺陷：(1)虽然得到的T网格不含有负值的雅克比行列式，但在Beizer因子提取后，不能保证所有的Beizer因子都有正雅克比行列式值。(2)输入的边界模型为零亏格，对于更加复杂的任意拓扑的结构没有进行讨论。(3)参数化映射和T网格质量优化步骤十分耗费时间。

之后,文献[3] 发展了上述方法，提出了任意复杂拓扑几何边界网格的三变量T样条实体化方法(如图5)。该文章在上述文献[2]基础上，将输入模型拓宽至任意复杂拓扑几何边界网格模型。并通过计算调和函数标量场和处理鞍点等过程进行体参数化，构建多重立方体参数域。随后，运用上述文献[2] 方法构建T 样条实体(案例如图6)。该方法具有很多优点：(1)三变量实体T样条直接在多重参数立方体上构建，且多重立方体可由任意复杂拓扑的几何模型自动生成；(2)实体T样条的表面为一张曲面并且只有极少数不规则节点；(3)所有T样条实体的雅克比行列式为正值，适合于等几何分析；(4)除了多重立方体边界角节点外，其余T样条实体的边界曲面为C2连续，保证了曲面的光顺性。但该文章也存在以下不足：(1)只考虑了含有莫尔斯鞍点的几何结构，没有考虑含有任意鞍点的几何结构；(2)没有考虑模型设计中的尖点特征。

图5 文献[3]构建T样条实体方法

图6 文献[3]由两亏格边界模型生成T样条实体和Beizer因子提取实例

图7 T样条曲面构建T样条实体的方法

文献[7] 提出了由T样条边界曲面构建三变量T样条实体的方法，可总结为图7。该文章输入模型为简单T样条边界曲面模型，要求T样条曲面为零亏格并且只含有八个奇异点。构建的T样条实体和初始T样条具有很好的一致性，有相同的边界表示和连续性，并且雅克比行列式为正值。在T样条实体的内部，除了不规则节点的局部区域外，连续性为C2。该方法也可用于由NURBS和局部细分B样条曲面构建三变量T样条实体(案例如图8)。

图8 文献[7]T样条曲面构建T样条实体实例

未来，任意复杂边界曲面模型(高亏格)的参数立方体构建和映射问题、T样条实体内部不规则节点处理问题、将初始T样条转变成适合分析的T样条实体问题、T样条实体局部细分问题和T样条实体边界曲面连续性问题仍是研究的热点。

2.2 NURBS、B样条实体的构建

NURBS、B样条实体构建的研究早于T样条实体，国内外学者也纷纷提出了不同的构建方法。目前，NURBS、B样条实体构建研究的关注热点主要集中在体参数化方法、三变量B样条实体的拟合迭代算法、优化重组内部控制顶点和权重、改善B样条实体的适合分析性等方面。其中，构建体参数化的方法有离散调和函数映射法、凸组合映射法、离散保形映射法等。

文献[8] 提出由零亏格边界三角网格模型构建B样条实体的方法，首先使用调和函数进行体参数化，由输入的三角网格生成四边形网格，再生成四面体网格并构建六面体网格。最后，以构建的六面体网格为基础，通过迭代拟合算法构建三变量B样条实体。文献[9] 提出扫略实体NURBS参数化建模方法并用于等几何分析，并对合适的参数化过程和边界插值条件的影响进行了论述。

文献[10] 通过血管模型的图像数据构建NURBS实体模型并用于等几何分析，构建方法如图9。但当模型复杂时，血管的分支会出现含有自交的区域，且如何评价构建的NURBS实体及如何提高网格的质量等问题仍有待解决。文献[11] 通过多盒实体的样条边界模型构建B样条实体并对于样条的参数化进行了研究，给出了不同计算域的适合分析的实体参数化方法。该文章通过解约束优化问题，使二次能量函数值最小化，来保证得到的体参数化结果达到最好，并保证没有自交部分且参数域部分有很好的均匀性和正交性。

图9 血管NURBS实体建模过程

文献[12] 提出基于梯度优化方法构建三变量B样条实体。其采用分而治之的方法通过找到内部控制顶点最合适的位置，运用区域聚合方法，保证最小雅克比行列式值为正，并通过最小化体积函数改善参数化质量。该方法很大地降低了问题的复杂性，减少了计算时间。文献[13]提出通过离散体参数化的方法，构建B样条实体。输入模型为边界三角网格模型，由每个内部顶点的几何信息构成一个线性系统方程。通过解此线性系统方程，完成离散体参数化过程。随后，该文章提出迭代算法来拟合三变量B样条实体。当控制顶点数量较多时，该拟合算法可以很好地控制运算时间的持续增长。

文献[14] 提出高效体参数化方法构建适合分析的NURBS实体。该文章提出莫比乌斯转换方法来优化参数化结果，之后建立适合分析的体参数化模型，通过边界再参数化方法和优化内部顶点和权重方法来构建适合分析的NURBS实体。

NURBS、B样条实体构建的方法相比于T样条实体构建较为简单，研究成果也更加丰富。未来，B样条实体的网格质量改善问题、高亏格复杂边界曲面模型的B样条实体构建问题、构建适合分析的体参数化问题仍是研究的热点。

3 总结与展望

等几何分析为CAE、CAD的无缝结合带来了曙光，构建可用于等几何分析的参数化样条实体也成为急需解决的问题。本文依据NURBS、B样条理论和T样条理论，着重介绍了T样条实体构建和NURBS、B样条实体构建研究进展，也介绍了现有实体研究成果的优点和存在的缺陷。目前，样条实体构建的相关研究仍处在初级阶段，存在很多有待解决的问题。未来，样条实体研究的方向如下：

(1)由任意高亏格复杂边界曲面模型构建样条实体的研究。目前，现有研究成果的输入模型大多为零亏格几何模型，少数研究针对一亏格或者两亏格几何模型。对于高亏格模型问题仍没有一套现有的处理方法。如何由任意复杂的CAD模型构建样条实体模型，仍是影响IGA广泛应用的关键问题。

(2)改善样条网格质量的研究。样条网格质量的好坏直接影响等几何分析的准确性和收敛性，并对计算时间和复杂度也产生较大影响。可以通过处理奇异节点、优化重组内部控制顶点和重置权重、光顺和优化处理等方法进行改善。这是一个约束优化问题，也是未来研究的热点。

(3)由初始样条网格构建适合分析的样条实体的研究。由于构建的三变量样条实体需要用于等几何分析，所以要求样条实体必须是适合分析的，即雅克比行列式值为正值。目前的研究中，构建的样条实体含有部分雅克比行列式值为负的区域。几何上表现为模型可能存在自交或者重叠部分，不适合等几何分析。虽然目前的研究出现了一些成果，但将初始样条网格模型转变成适合分析的样条实体模型是研究的热点问题。

(4)样条实体边界曲面的连续性问题研究。目前，对于构建的三变量样条实体的边界曲面的连续性问题研究较少，且在奇异节点处连续性突减，如何改善样条实体表面的连续性问题也是未来研究热点。

[1] Hughes T J R, Cottrell J A, Bazilevs Y. Isogeometric Analysis: CAD, Finite Elements, NURBS, Exact Geometry and Mesh Refinement[J]. Computer Methods in Applied Mechanics and Engineering, 2005, 194(39): 4135- 4195.

[2] Zhang Y, Wang W, Hughes T J R. Solid T- spline Construction from Boundary Representations for Genus- zero Geometry[J]. Computer Methods in Applied Mechanics and Engineering, 2012, 249: 185- 197.

[3] Wang W, Zhang Y, Liu L, et al. Trivariate Solid T- spline Construction from Boundary Triangulations with Arbitrary Genus topology[J]. Computer- Aided Design, 2013, 45(2): 351- 360.

[4] Wang W, Zhang Y, Xu G, et al. Converting an Unstructured Quadrilateral/hexahedral Mesh to a Rational T- spline[J]. Computational Mechanics, 2012, 50(1): 65- 84.

[5] Sederberg T W, Zheng J, Bakenov A, et al. T- splines and T- NURCCs[C]//ACM Transactions on Graphics (TOG), 2003, 22(3): 477- 484.

[6] Escobar J M, Cascón J M, Rodríguez E, et al. A New Approach to Solid Modeling with Trivariate T- splines Based on Mesh Optimization[J]. Computer Methods in Applied Mechanics and Engineering, 2011, 200(45): 3210- 3222.

[7] Zhang Y, Wang W, Hughes T J R. Conformal Solid T- spline Construction from Boundary T- spline Representations[J]. Computational Mechanics, 2013, 51(6): 1051- 1059.

[8] Martin T, Cohen E, Kirby M. Volumetric Parameterization and Trivariate B- spline Fitting Using Harmonic Functions[C]//Proceedings of the 2008 ACM Symposium on Solid and Physical Modeling. ACM, 2008: 269- 280.

[9] Aigner M, Heinrich C, Jüttler B, et al. Swept Volume Parameterization for Isogeometric Analysis[M]. Berlin Heidelberg:Springer , 2009:45.

[10] Zhang Y, Bazilevs Y, Goswami S, et al. Patient- specific Vascular NURBS Modeling for Isogeometric Analysis of Blood Flow[J]. Computer Methods in Applied Mechanics and Engineering, 2007, 196(29): 2943- 2959.

[11] Xu G, Mourrain B, Duvigneau R, et al. Analysis- suitable Volume Parameterization of Multi- block Computational Domain in Isogeometric Applications[J]. Computer- Aided Design, 2013, 45(2): 395- 404.

[12] Wang X, Qian X. An Optimization Approach for Constructing Trivariate B- spline solids[J]. Computer- Aided Design, 2014, 46: 179- 191.

[13] Lin H, Jin S, Hu Q, et al. Constructing B- spline Solids from Tetrahedral Meshes for Isogeometric Analysis[J]. Computer Aided Geometric Design, 2015, 35: 109- 120.

[14] Xu G, Mourrain B, Galligo A, et al. High- quality Construction of Analysis- suitable Trivariate NURBS Solids by Reparameterization methods[J]. Computational Mechanics, 2014, 54(5): 1303- 1313.

[责任编辑：张永军]

The Summary of Construction of Spline Solid from Boundary Representation or Spline Surface

WANG Hui- ying1, ZHANG Yi- gang2，LI Huai- ying3

(1.School of Xueyan Trade，Anhui Finance and Trade Vocational College,Hefei 230601；2.Department of Architecture Engineering，Hefei University,Hefei 230601；3. Key Laboratory of Process Optimization and Intelligent Decision-making for Ministry of Education, Hefei University of Technology, Hefei 230009,China)

Isogeometric analysis(IGA) brings the tight integration of CAD and CAE. How to generate trivariate spline solid becomes an urgent task for the development and popularized application of IGA. This paper presents the review of NURBS and T- spline basic theory, and emphasizes the research progress of NURBS、B- spline and T- spline solid, based on the perspective of isogeometric analysis. In addition, this paper analyzes the advantages and deficits of the research achievement. Finally, this paper discusses the deep study problems of solid construction in the future.

isogeometric analysis； NURBS、B- spline；T- spline；construction of spline solid

2017-01-10

2017-03-03

国家“863”云制造主题项目(2015AA042101)、国家自然科学基金重大研究计划培育项目(91546108)、国家自然科学基金项目(71301041)、安徽省高校自然科学重点项目(KJ2016A009，KJ2017A860)资助。

王会颖(1969— ),女,安徽萧县人,安徽财贸职业学院雪岩贸易学院副教授、博士,研究方向:群体智能、云制造；章义刚(1965— ),男, 安徽南陵人,合肥学院建筑工程系副教授, 研究方向：智能计算。

TH126

A

2096-2371(2017)02-0057-07