Three-Dimensional Problem of the Compressible Water-gas Mixture Impacting on Rigid Plates
GE Liang,ZHANG Zhong-yu,YAO Xiong-liang,SUN Long-quan
(College of Shipbuilding Engineering,Harbin Engineering University,Harbin 150001,China)
Three-Dimensional Problem of the Compressible Water-gas Mixture Impacting on Rigid Plates
GE Liang,ZHANG Zhong-yu,YAO Xiong-liang,SUN Long-quan
(College of Shipbuilding Engineering,Harbin Engineering University,Harbin 150001,China)
On the basis of the mass and momentum conservation,an inviscid model is established to investigate water-gas mixture impact problems,for which weak compressibility should be taken into consideration.The Internal Doubly Asymptotic Approximation method is adopted to solve the governing equation.A separate treatment on the free surface and rigid plate is used to satisfy the boundary conditions.The numerical results are in excellent agreement with those calculated by the Autodyn solver and the corresponding theoretical formula.The influence of volume fractions of gas on the impact load characteristics is investigated.The results reveal that with the volume fraction of gas increasing,the peak of load will decrease significantly.Meanwhile,the pulse width and the minimum value of the pressure will increase for homogeneous water-gas mixture impact.
water-gas mixture;compressibility;internal DAA method
0 Introduction
Water jet impact problems have been paid great attention since they are common phenomena in many fields,such as the collapse of a spherical bubble in an underwater explosion, green water and wave impact.The impact pressure may cause material damage,although it only lasts a short period.With the development of engineering technology in the recent years,the gas is taken into account in the impact process,such as‘cushion effect’[1],which occurs when the flat structures entry into the water with a high velocity.Since when the flat structure falling fast,a portion of the air will be trapped and push into the water by flat structure.Thus,a layer of air cushion is formed.The formation of air cushion[2]was investigated experimentally, and the experimental results showed that the expansion and compression of air cushion would make the hydrodynamic pressure pulsating in the anaphase of the impact process.Another experimental study was conducted[3],in which the Slingshot Impact Testing System was used to launch objects with different speeds and dead rise angles.The air cushion was captured at a small dead rise angle by a high-speed camera.The problem of two-dimensional unsteady im-act on a layer of liquid which is mixed with air near the wall is solved with the linear theory of the velocity potential[4].The air cushion was also studied using the finite element method[5]. It was found that the impact pressure lasted a short period and the drop splashing only appeared latterly during the process of the plate entering the water.
The phenomenon is similar to the above when the high-speed slender with cavitation exiting from the water[6].The cavitation begins to be compressed,and the water-gas mixture will impact on the surface of slender,which will be subjected to a large impact force.However,due to the involved gas,the problem of water-gas mixture impact becomes more complex.Since the mixture density changes along with gas volume fraction increasing,the acoustic velocity of the mixture will change as well.Fortunately,the formula for acoustic velocity was derived for the homogeneous mixture[7],with the assumption that one phase was the elastic boundary of another phase,the results of which were in good agreement with the experimental data[8].
To our knowledge,previous studies have achieved some characteristics of water impact, but few studies have been carried out for water-gas mixture impact problems.In this work,a three-dimensional inviscid model is proposed for the water-gas mixture impact problems.The influence of gas volume fractions on impact load characteristics is analyzed,which aims at providing some reference for the design of marine engineering structures.
1 Mathematical model and numerical procedure
The water-gas mixture domain is cylindrical with the diameter D and the length L.A Cartesian coordinate system o-xyz is introduced with its origin located at the center of the plane z= 0.Initially the mixture moves to the rigid plate at an instant velocity V.Sband Sfare the solid boundary and free surface boundary,respectively,and L is the length of fluid domain,as shown in Fig.1.Then the continuity equation can be obtained as follows:

where U is the velocity of the water-gas mixture and ρhis the density of the water-gas mixture.
Furthermore,we assume that the mixture is homogeneous. Then based on the mixture model,the density of mixture is only dependent on the volume fraction of gas and can be expressed as

where ρland ρgare the densities of water and gas,and α is the volume fraction of gas.
The mixture is inviscid and weakly compressible,and the gravity and surface tensor are ignored,so we can obtain the momentum equations:
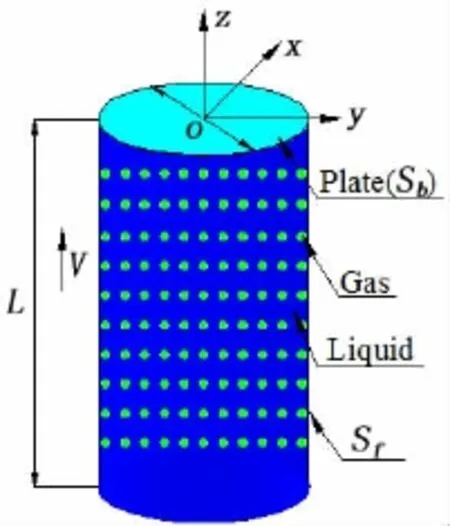
Fig.1 Sketch of the water-gas mixture impact problem

where p is the impact pressure.Fortunately,the change of ρhis very gentle and thus ρhcan be assumed to be a constant.Then Eq.(3)can be reduced as

Based on the state of mixture,we have that:

where chis acoustic velocity of the mixture[7],which can be expressed as:

where cland cgare acoustic velocities of water and gas,respectively.
Together with Eqs.(1-6),we can obtain the following governing equation for water-gas impact:

where φ0is the disturbed potential.
The no-flux condition normal to the rigid plate takes the form with the linear approximation:

Note that the normal n goes into the fluid at a point on the plate.
The Internal Double Asymptotic Approximations[9-10]is an effective boundary element method for the general solution in the Eq.(7).These approximations approach exactness in both the early time and the later approximation.In the early approximation,when the time is small, the velocity potential is only linking to the surface around the point Q,so we can introduce the second-order early approximation

where rQis the position vector of the point Q,κ and s˙nare the local mean curvature and the normal velocity of the point Q,respectively.
The later approximation corresponds to that t is large.Then the Taylor expansion is used for the retarded variables and the second order form is taken
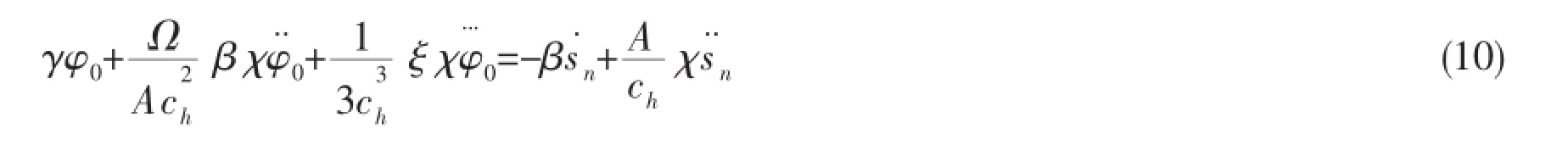
where Ω is the volume of the fluid domain,A is the area of the surface,and the spatial integral operators can be defined by:

Based on the operator matching method for the early approximation and later approximation,we can introduce the second order DAA for internal acoustic domain

where the operators M,Π,d are defined by
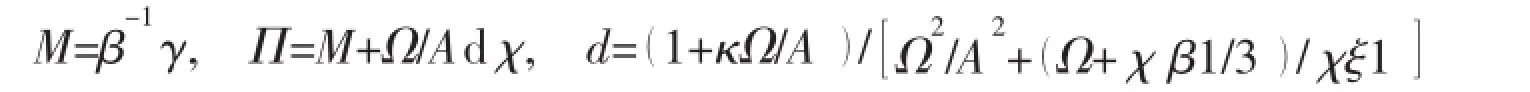
The fluid boundaries are discretized into a set of triangular elements with N nodes.Each element is mapped into the isosceles right triangle[11],and the shape function is chosen as

Thus the spatial integral operators can be obtained numerically at each element as follows:
The spatial integral operators can be calculated by assembling the above equations from each element,and then the Eq.(10)can also be rewritten in the matrix form
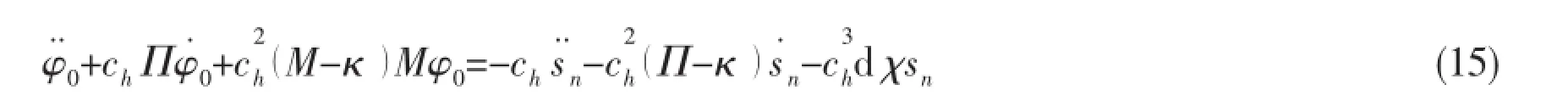
The velocity potential of the vertexes at the free surface is moved to the left hand side of Eq.(15)and the displacement of the nodes is moved to the right.The Eq.(15)then becomes


where the superscript or subscript b denotes the node at the solid boundary and f denotes the nodes at the free surface.
The forward difference scheme is adopted to solve the above equation and the value of the time step is chosen as the following equation[12]

The intersections of the solid boundary and the free surface should be treated especially since the normal may not be continuous,which has an influence on the convergence[13].Similar to the Ref.[14],the spatial integral operators at the intersections can be split into two parts:one from the integration over the solid boundary and the other from the integration over the free surface.
2 Results and discussions
2.1 Comparisons for the water impact problem
The present method is first verified by the problem of water impact,which means that the volume fraction of gas is zero.The diameter of fluid domain is 1 m and the length is 20 m.The boundaries of fluid domain are divided into a set of 1 620 triangle elements with 812 nodes. Note that all the following cases use the same set of elements.The same case is also solved by Autodyn-3D solver[15],and the fluid domain is divided into the 400 000 hexahedron elements. The two-dimensional impact problem was solved by Autodyn-2D solver[15]with the rectangle domain(1 m×20 m),which is divided into the 100 000 quadrilateral elements.The SNL model is chosen for water.

Fig.2 Comparisons of(a)maximum pressures and(b)minimum pressures due to the change of velocity by different solvers
Due to the change of velocity,the comparisons of maximum and minimum pressures at the center are shown in Fig.2.It can be seen that the maximum pressures obtained by the three solvers are almost identical,while there are significant differences in minimum pressures between the Autodyn-2D and the present method or Autodyn-3D.It should be noted that the two-dimensional domain is infinite compared with the three-dimensional domain,and no reflect pressure wave is generated at infinity.Therefore,the minimum pressures obtained by Autodyn-2D will be larger than those obtained by the present method or Autodyn-3D.
2.2 Characteristics for the water-gas mixture impact
The characteristics of the loads for the water-gas mixture impact are investigated with different volume fractions of gas.The results are non-dimensional in order to be compared with those for water impact,including the time t,the impact pressure p and the resultant.The dimension D is the length scale,the velocity V is the velocity scale,and the water hammer pressure ρCV is the pressure scale,here ρ is the density of water and C is the acoustic velocity of water.Thus we have:


Tab.1 Comparisons of peak pressure between the present results and the empirical results
Tab.1 provides the comparisons of peak pressure between the present results and the empirical results[7,16]with the volume fraction of gas varying from 1‰to 4‰.It is found that the two methods have good agreements and the maximum relative error is 0.42%.

Fig.3 History of the impact pressures at the center with different volume fractions of gas

Fig.4 History of the resultants with different volume fractions of gas
Fig.3 presents the history of the impact pressure at the rigid plate center with volume fraction of gas varying from 1‰to 4‰.It can be seen that with the volume fraction of gas increasing,the peak pressure will decrease gradually,but the pulse width will increase.In addition,the peak pressure is 1 and the pulse width is 1 for water impact from the Ref.[16].So it can be obtained obviously that due to the presence of gas,the peak pressure will reduce significantly and the pulse width will increase simultaneously.As the gas exists in the form of bubbles with the small radius in the physical world,a very low acoustic velocity can be obtained according to the Eq.(6),even at small gas volume fraction.The acoustic velocity attenuation can be accounted for by considering the individual response of bubbles to the pressure wave.In other words,the state of mixture has changed as a result of the involved gas.The acoustic velocity of mixture reduces more greatly than those of water,and it will take more time for reflected pressure wave to propagate into the center of plate,which makes the impact pressure pulse widened.The history of resultant for the rigid plate is shown in Fig.4,which has the similar tendency with those of impact pressure at the rigid plate center.

Fig.5 Contours of impact pressure at the time T=0.5 with(a)α=1‰;(b)α=2‰;(c)α=3‰;(d)α=4‰
The contours of impact pressure with different volume fractions of gas at T=0.5 are shown in Fig.5.At the initial time,the compressibility of the liquid is of significance.Most of regions are subjected to large impact pressure and the pressure is comparable to ρhchV(chis acoustic velocity of mixture).The mixture may have the similar impact property with water, though the gas exits in the form of bubbles in the water.
Fig.6 provides the contours of impact pressure at the time when the resultants reach the minimum respectively.At this moment,there exists negative pressure at the vicinity of thecenter due to the reflected pressure wave generated by the free surface.In practice,the negative pressure will lead to the appearance of cavities attached to the rigid plate.Then the pressure increases again,which leads to a collapse of the bubbles with the formation of new impact.It can also found that gas can restrain negative pressure effectively as the absolute values of the minimum pressures decrease with the volume fraction of gas.The impact pressures of mixture decline rapidly and stabilize in the later jet impact.After this time,the steady state is reached and the pressure approaches hydrodynamic pressure.

Fig.6 Contours of impact pressure at the time of the minimum resultant with(a)α=1‰,T=2.9;(b)α=2‰,T=3.8;(c)α=3‰,T=5.2;(d)α=4‰,T=5.6
3 Conclusions
A three-dimensional inviscid physical model is established for the compressible watergas mixture impact problems.The Internal Doubly Asymptotic Approximation method was adopted to solve the water-gas mixture impact problems.The results show that the compressibility of the liquid is dominant and gas plays an important role in the impact process.As the gas exists in the form of bubbles with the small radius in the physical world,the state of mixture will change.So the peak of load can decrease significantly with the volume fraction of gas increasing.Rapid temporal evolution of the pressure can be observed during this stage.This behavior can be partly explained by the pressure wave propagated from the free surface.
[1]Chuang S L.Experiments on flat bottom slamming[J].Journal of Ship Research,1966,10:10-17.
[2]Lin M C,Shieh L D.Simultaneous measurements of water impact on a two-dimensional body[J].Fluid Dynamics Research,1997,19(3):125-148.
[3]Huera-Huarte F J,Jeon D,Gharib M.Experimental investigation of water slamming loads on panels[J].Ocean Engineering,2011,38:1347-1355.
[4]Korobkin A A.Two-dimensional problem of the impact of a vertical wall on a layer of a partially aerated liquid[J].Journal of Applied Mechanics and Technical Physics,1996,47:643-653.
[5]Chen Z,Xiao X,Wang DY.Simulation of flat bottom structure slamming[J].China Ocean Engineering,2005,19(3):385-394.
[6]Wang Y W,Huang C G,Du T Z,et,al.Shedding phenomenon of ventilated partial cavitation around an underwater projectile[J].Chinese Physics Letter,2012,29(1):014601-04.
[7]Nguyen D L,Winter E R F,Greiner M.Sonic velocity in two-phase systems[J].Journal of Multiphase Flow,1981,7:311-320.
[8]Coste C,Laroche C.Acoustic behaviour of a liquid/vapour mixture in a standing-wave tube[J].J Fluid Mech,1993,246:67-89.
[9]Geers T L.Doubly asymptotic approximation for transient motions of submerged structures[J].The Journal of the Acoustical Society of America,1978,64:1500-1508.
[10]Geers T L,Zhang P Z.Doubly asymptotic approximations for submerged structures with internal fluid volumes:Formulation[J].Journal of Applied Mechanics,1994,61:893-899.
[11]Ye X,Yao X L,Zhang A M,Pang F Z.The motion and acoustic radiation characteristics for cavitation in the compressible vortex fluid[J].Acta Phys.Sin.,2013,62:114702.
[12]Zhang A M,Wang S P,Wu G X.Simulation of bubble motion in a compressible liquid based on the three dimensional wave equation[J].Engineering Analysis with Boundary Elements,2013,37:1179-1188.
[13]Dommermuth D,Yue D K P.Numerical simulations of nonlinear axisymmetric flows with a free surface[J].Journal of Fluid Mechanics,1987,178:195-219.
[14]Ni B Y,Zhang A M,Wu G X.Numerical simulation of motion and deformation of ring bubble along body surface[J].Applied Mathematics and Mechanics,2013,34(12):1495-1512.
[15]ANSYS,ANSYS/Autodyn[K].User Documentation,Version 6.1,2007.
[16]Sun S L,Hu J,Hu J Z.Impact of a compressible water column on an elastic plate[J].Journal of Ship Mechanics,2013, 17(9):1031-1037.
三维可压缩水气混合物射流冲击平板特性研究
葛亮,张忠宇,姚熊亮,孙龙泉
(哈尔滨工程大学船舶工程学院,哈尔滨150001)
根据质量和动量守恒方程,忽略流体的粘性,计入流体的可压缩性,建立水气混合物射流冲击平板问题的物理模型。采用内域双渐进方法对控制方程进行数值离散,平板边界和水域分别进行处理以满足各自的边界条件。数值结果与解析解及Autodyn的数值结果吻合较好。在验证方法合理性的基础上,深入地分析了含气量对射流冲击载荷特性的影响规律。数值结果表明:随着含气量的增加,冲击压力峰值将会显著地降低,而脉宽和射流冲击压力的极小值都会增大。
水气混合物;可压缩性;内域DAA方法
O353.4
:A
葛亮(1989-),男,哈尔滨工程大学船舶工程学院博士研究生;
1007-7294(2017)03-0309-09
O353.4
:A
10.3969/j.issn.1007-7294.2017.03.006
张忠宇(1988-),男,哈尔滨工程大学船舶工程学院博士研究生;
姚熊亮(1963-),男,哈尔滨工程大学船舶工程学院教授,博士生导师;
孙龙泉(1983-),男,哈尔滨工程大学船舶工程学院副教授。
Received date:2016-10-27
Biography:GE Liang(1989-),male,a graduate student in Harbin Engineering University; ZHANG Zhong-yu(1988-),male,a graduate student in Harbin Engineering University,E-mail:zhangyu061031@126.com;
YAO Xiong-liang(1963-),male,professor/tutor.
——关于葛亮研究的总结与思考
- 船舶力学的其它文章
- Measuring the Acoustic Properties of Underwater Coating Material under Pressure-Acoustic Impedance Method
- Modal Pole Placement for Coupled Structural Acoustic System Based on Reduced Order Model
- Effect of Adiabatic Shear on Penetration Properties of Water-back Plate
- Safety Assessment of An Aging Offshore Jacket Platform by Integrating Analytic Hierarchy Process and Grey Clustering Method
- A Study on Connector Loads of Very Large Floating Structures near Islands and Reefs
- Three Dimensional Crack Path Prediction of Brittle Fracture in Weldment Under Fatigue Load

