Three Dimensional Crack Path Prediction of Brittle Fracture in Weldment Under Fatigue Load

YANG Da-peng,PAN Hai-yang,ZHAO Yao,LI Tian-yun

(1.Mechanical Engineering Department,Zhengzhou Technical College,Zhengzhou 450121,China;2.School of Naval Architecture&Ocean Engineering,Huazhong University of Science and Technology,Wuhan 430074,China;3.Zheng Zhou Technical College,Urban Rail Transport Department,Zhengzhou 450121,China)

Three Dimensional Crack Path Prediction of Brittle Fracture in Weldment Under Fatigue Load

YANG Da-peng1,2,PAN Hai-yang3,ZHAO Yao2,LI Tian-yun2

(1.Mechanical Engineering Department,Zhengzhou Technical College,Zhengzhou 450121,China;2.School of Naval Architecture&Ocean Engineering,Huazhong University of Science and Technology,Wuhan 430074,China;3.Zheng Zhou Technical College,Urban Rail Transport Department,Zhengzhou 450121,China)

Based on a second order perturbation method,three dimensional fatigue stress intensity factors are analyzed for a curved crack.The method is extended to obtain an approximate representation of a three dimensional fatigue stress intensity factors at the tip of a curved crack.A fatigue energy release rate due to three dimensional curved crack growth can be calculated by using Irwin’s formula.Considerations are made for a three dimensional fatigue curved crack in materials with inhomogeneous fracture toughness.Paths of a brittle three dimensional fatigue curved crack propagating along a welded joint are predicted as a practical application of the present method,where the effects of fatigue applied stresses,residual stresses,and material deterioration due to welding are taken into considerations.

three dimensional fatigue stress intensity factor;curved crack;a second order perturbation method;a fatigue energy release rate

0 Introduction

Perturbation analyses for quasi-static slightly curved crack were first performed by Banichuk[1],and Goldstein and Salganik[2-3],in which they satisfied the boundary conditions approximately along the slightly curved crack surfaces with the use of Muskhelishvili’s complex potentials.Having obtained a rather simple expression of stress intensity factors by using the same method,Cotterell and Rice[4]examined the crack growth path of a semi-infinite crack in an infinitely extended plane.A second order perturbation solution was calculated by Karihaloo et al[5],in which they considered a straight crack of finite length with slightly kinked-curved extension in an unbounded plane that was subjected to uniaxial tensile stress at infinity.First order perturbation analyses were also performed by Sumi et al[6-7]for a straight crack in a fi-nite body with a slightly branched and curved extension.The shape of branched and curved extension was approximated by a continuous function with three shape parameters,and the approximate stress intensity factors at the extended crack tip were obtained in terms of these parameters and the near tip stress field parameters ahead of the crack tip prior to its extension,where the effects of the geometry of the domain were also taken into account.Yang et al[8]have obtained approximate descriptions of the stress intensity factors at the two dimensional curved crack tip,where the cracked body was subjected to dynamic loads.Wu[9],Amestoy and Leblond[10]have acquired the exact asymptotic results of the path of a crack warp ramification and the stress intensity factors existing in crack warp ramification tip.But as far as application of second order perturbation solution is concerned,the grand old men’research productions were all localized in those of crack warp development in weldment while enduring loads of static state on linear elasticity conditions[13].At the present time,operators of science and technology have not taken measure of second order perturbation analysis to work over problems which a three dimensional curved crack develops and extends in crack body enduring fatigue loads in elasticity state or quasi elasticity state[14-15].

In this paper,a three dimensional curved crack tip fatigue stress intensity factors have been analyzed and calculated on the basis of the research production of Sumi et al.Furthermore,the shape of a three dimensional curved crack has been predicted when crack body was received fatigue loads.When received fatigue loads,the original three dimensional straight crack will stretch to incurvate because of uneven fracture toughness or material inhomogeneity such as a local degradation zone.Using a second order perturbation analysis solution,fracture behaviors of a three dimensional brittle fatigue curved crack will be researched into.

1 Approximate description of a three dimensional curved crack in a finite body receiving fatigue load

1.1 Modification of the second order perturbation solution to a three dimensional fatigue curved crack

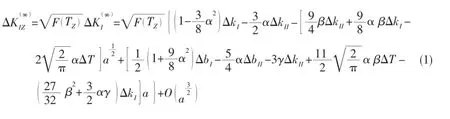
Fig.1 A three dimensional curved crack in a finite body enduring fatigue load

And the finite body corrections of the fatigue stress intensity factor amplitudes at the three dimensional curved crack tip are given by：

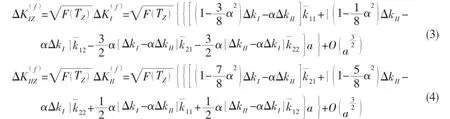
Therefore,the three dimensional fatigue stress intensity factor amplitudes ΔKIZand ΔKIIZat the three dimensional curved crack tip are respectively given by：

where ΔKIZand ΔKIIZare the three dimensional dynamic stress intensity factors which arecontaining three axis stress constraints. Thereinto[16-17]：

where TZis off surface confinement factor[16-17].

1.2 Criterion of the three dimensional curved crack unsteady extending in weldment when enduring fatigue load

Let fatigue fracture toughness of the three dimensional crack body be KCZ,let type one fatigue fracture toughness of the three dimensional crack body be KICZ,let type two fatigue fracture toughness of the three dimensional crack body be KIICZ,let stress intensity factor variation amplitude threshold value be ΔKthZ,let stress ratio of fatigue load be R,let curved crack length be LZ,thereupon calculation formula of the three dimensional fatigue curved crack steady propagation rate will be acquired as follows：

where C and m are material constants.

Condition or criterion of three dimensional fatigue curved crack steady existing and not extending：

Condition or criterion of three dimensional fatigue curved crack steady extending：

Condition or criterion of three dimensional fatigue curved crack unsteady extending：

If combining Eqs.(5-11),we can know the extending state of the three dimensional fatigue curved crack.

2 Discussion on fatigue crack path criteria

2.1 Fatigue energy release rate

Based on the research production of Bilby and Cardew[11],the dynamic elastic energy release rate ΔGZ,due to the slightly branched and curved crack extension in homogeneous materials receiving dynamic loads can be calculated as：

where μ and ν are shear modulus and Poisson’s ratio,respectively,and ΔKIZand ΔKIIZare the three dimensional dynamic stress intensity factors at the extended crack tip.According to subsistent research products[8,16],ΔGZis given by：

The three dimensional dynamic energy release rate of three dimensional curved crack is initially governed by the first term G0Zwritten as：

The first and second variations of G0Zare calculated as：

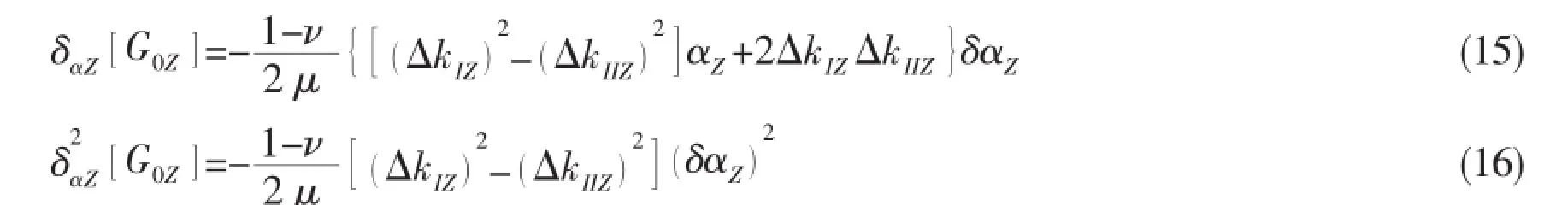
which gives rise to the three dimensional maximum dynamic elastic energy release rate of the crack body.

One of the criteria often used in crack path prediction is the condition of local symmetry, which requires that ΔkIIZvanishes along curved crack[8].When the crack body is receiving dynamic loads,this criteria will demand that the discretionary ΔkIIZdue to dynamic loads all vanishes along curved crack extension.This means that in homogeneous materials the both criteria designate equivalent crack paths within the second order approximation theory.

2.2 The effects of inhomogeneous distribution of three dimensional fatigue fracture toughness

Here a crack under pure Mode-I fatigue loading condition is considered,whose tip intersects a specially oriented line degradation zone at angle αZ*(see Fig.2),and where the critical fatigue energy release rates for the base material and the degraded material are ΔGCZand ΔGCZ*,respectively.The three dimensional fatigue stress intensity factor at the instance of fracture is calculated from Eq.(14)and given by：

By comparison,if the crack extends in the degraded zone,the kink angle is αZ*and corresponding the fatigue stress intensity factor prior to the crack extension is also calculated from Eq.(14)as：

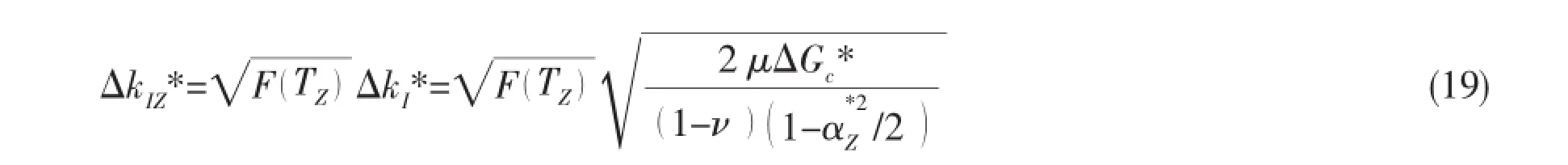
3 The three dimensional curved crack path prediction of brittle fracture in weldment receiving fatigue load

3.1 An analytical model of a brittle fatigue crack in weldment

Based on the aforementioned quasi-static crack analysis,investigations are made for a transverse welded joint in an infinite plate under a uniaxial tensile stress Δσawhich is dynamic.The sum of the longitudinal component of welding dynamic residual stress σrand the outer dynamic stresses Δσbwhich is acting parallel to the welded joint is accordingly fatigue in the region.Here,let Δσr′=σr+Δσbin order to analyze them conveniently.As is shown in Fig.2,the initial crack of length 2Hzis assumed to be parallel to the welding line.Material deterioration is observed along the heat affected zone,which is modeled as a line degradation being also parallel to the welded joint with the distance Lsfrom the initial crack line.The resistance forces of three dimensional fatigue curved crack propagation can be denoted by ΔGCZfor base and weld metals,and ΔGCZ*for the heat affected zones respectively.Brittle fatigue crack propagation is assumed to occur from the right hand side of the crack tip where the origin of the Cartesian coordinate system O-X1X2X3is established.Since a slightly warp ramifi-cation extension under fatigue stresses may be expected,the fatigue crack intersects the degradation line at angle αZ*with x1=hz*.

Fig.2 A mathematical modeling of three dimensional curved crack propagation along a welded joint receiving fatigue load

The stress field parameters at the original crack tip are obtained as：

3.2 Three dimensional fatigue crack path prediction

As was discussed in the previous subsection,in the case where the initial crack tip is contained in a homogeneous material receiving fatigue loads,a fatigue crack path can be determined by the local symmetry criterion,which is equivalent to the condition ΔkIIZ=0 along the curved trajectory.The three dimensional fatigue curved crack path is approximated by Eq.(23), and the shearing mode of stress intensity factor can be approximated by the first order terms of Eq.(6).Putting the equation to be identically zero and disregarding the second order terms, the shape parameters of the fatigue curved crack path are determined as：

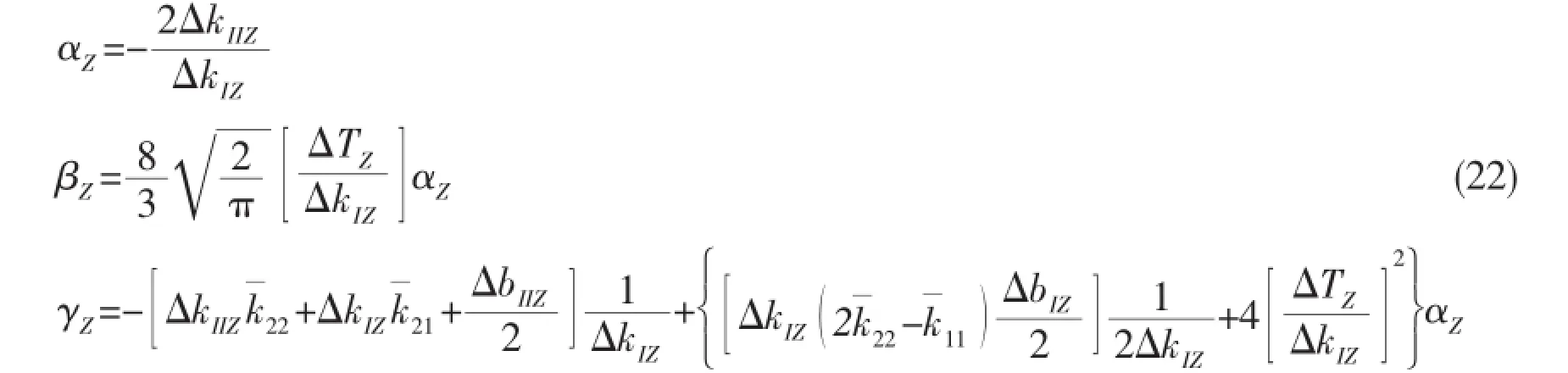
Substituting Eq.(21)into Eq.(22),equation αZ=βZ=γZ=0 will be obtained.

This three dimensional straight fatigue crack extension could occur only for the perfect system,which means that the loading condition and the geometry have the perfect symmetry with respect to the crack line.Let us study the case in which non-collinear crack propagation is caused by some load induced disturbances in the system with a small initial three dimensional kink angle αZat the original crack tip used as the imperfection parameter of the system.

where αZ,βZand λZare the shape parameters.

The three dimensional fatigue crack path stability is then examined by considering the second and third terms of Eq.(23).The effect of fatigue crack path stability should be examined by means of the rest of the terms being proportional to αZ.So the three dimensional fatigue crack path stability should be evaluated by the quantity range ΔDSZthat is expressed as：

where ΔBSZand ΔCSZare the three dimensional amplitude parameters representing the destabilizing effect against the fatigue curved crack：

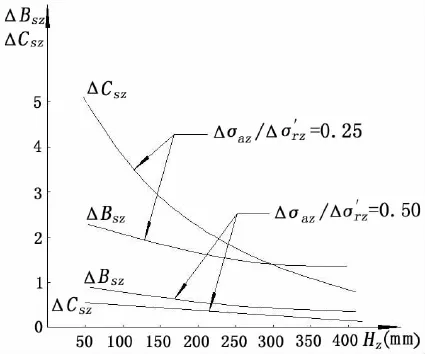
Fig.3 Three dimensional fatigue curved crack path destabilizing factors

Fig.3 shows the crack path destabilizing factors ΔBSZand ΔCSZfor the present analysis model,where the ratios of applied fatigue stress and the sum of the outer fatigue stress and the residual stress are chosen as 0.25 and 0.5.From the moment t=0(s)the approximate moment t=5(s),the fatigue crack path destabilizing factors ΔBSZand ΔCSZare increasing,and will get up to maximum approximately when t=5(s).In the case where the applied fatigue stress level is relatively low compared with the sum of the outer fatigue stress and the residual stress,and where the size of the initial crack is relatively small,these parameters have large values.This means that fatigue crack paths of low stress brittle fracture initiated from a small initial crack at weldment can most probably be branched into the base metal approximately when the fatigue crack path destabilizing factors get up to maximum.

As the fatigue crack further extends,it begins to intersect the line degradation zone.Here the question presents itself on whether the fatigue crack intersects the zone and penetrates into the base metal,or whether it branches to the heat affected zone,where the fracture toughness is lower than that of the base metal.For the sake of solving the question,the angle αZ* is calculated,which is shaped by the fatigue crack and the degradation line by means of equa-tions(21),(22)and(23).The condition of three dimensional fatigue crack extension along the degradation line could be acquired by using inequality(20).

3.3 Results and discussions

In this subsection,fatigue crack paths of brittle fracture in weldments are analyzed based on the numerical results.Numerical calculations are performed for the cases in which the initial half crack length is chosen as H=100,200,300,400 and 500 mm.Since the distance LSZ, between the initial crack line and the degradation line is of the order of the beads width,it is chosen as 25 or 50 mm.The imperfection parameter αZis selected as 0.5,1.0,1.5,2.0,2.5 and 3.0 degrees.

Fig.4 Critical relations between the material degradation and the applied stress or the outer stress which is fatigue for various initial three dimensional crack lengths;three dimensional fatigue cracks penetrate into the base metal for the conditions corresponding to the upper left regions with respect to the curve

4 Conclusions remarks

In this paper,three dimensional fatigue brittle crack development in a finite body is analyzed by using a second order perturbation solution.And it is applied to examine the relation between the fatigue energy criterion and the fatigue stress criterion for the fatigue crack path prediction.As far as homogeneous materials are concerned,both criteria designate equivalent fatigue crack paths within the second order approximation theory.It should be contrasted for fatigue crack paths in materials with inhomogeneous fracture toughness,in which the energy criterion predominates over the stress criterion.As a practical application of the method,morphological characteristics of three dimensional fatigue brittle fracture in weldment are studied, and the critical curves for the three dimensional fatigue crack propagation along the degraded zone have been acquired considering many factors such as the applied fatigue stresses,the welding residual stresses,the localized material deterioration and the defect sizes.

There are a large number of three dimensional curved cracks in ship structures,and three dimensional curved cracks are more than two dimensional curved cracks,so the research of this paper is very meaningful.

[1]Banichuk N V.Determination of the form of a curvilinear crack by small parameter technique,Izv[J].An SSSR MTT, 1970,7-2：130-137.(in Russian)

[2]Goldstein R V,Salganik R L.Plane problem of curvilinear cracks in an elastic solid,Izv[J].An SSSR MTT,1970,7-3：69-82.(in Russian)

[3]Goldstein R V,Salganik R L.Brittle fracture of solids with arbitrary cracks[J].Int.J Fracture,1974,10：507-523.

[4]Cotterell B,Rice J R.Slightly curved or kinked cracks[J].Int.J Fracture,1980,16：155-169.

[5]Karihaloo B L,Keer L M,Nemat-Nasser S,Oranratnachai A.Approximate description of crack Kinking and curving[J].J Appl.Mech.,1981,48：515-519.

[6]Sumi Y,Nemat-Nasser S,Keer L M.On crack branching and curving in a finite body[J].Int.J Fracture,1983,21：67-79;Erratum,Int,J Fracture,1984,24：159.

[7]Sumi Y.A note on the first order perturbation solution of a straight crack with slightly branched and curved extension under a general geometric and loading condition[J].Engng.Fracture Mech.,1986,24：479-481.

[8]Yang Dapeng,Zhang Xueyan,Zhao Yao,Bai Ling,Zhao Hui.Crack path prediction of brittle fracture in weldment under dynamic loads[J].Journal of Ship Mechanics,2012,16(3)：254-270.

[9]Wu C H.Explicit asymptotic solution for the maximum-energy-release-rate problem[J].Int.J Solids Structures,1979,15：561-566.

[10]Amestoy M,Leblond J B.On the criterion giving the direction of propagation of cracks in the Griffith theory[J].Comptes Rendus,1985,301,serie II：969-972.(in French)

[11]Bilby B A,Cardew G E.The crack with a kinked tip[J].Int.J Fracture,1975,11：708-712.

[12]Sumi Y,Nemat-Nasser S,Keer L M.On crack path stability in a finite body[J].Engng.Fracture Mech.,1985,22：759-771.

[13]Richard H A.Theoretical crack path prediction.(Institute of Applied Mechanics,University of Paderborn);Fulland M, Sander M S.Fatigue and fracture of engineering materials and structures[J].2005,28(1-2)：3-12.

[14]Wang Lei,Wu Jiankang.Flow behavior in microchannel made of different materials with wall slip velocity and electroviscous effects[J].Acta Mechanica Sinica,2010,26(1)：73-80.

[15]Zhang Weifeng,Feng Hua.The wavelet analysis of vibration detection for structure’s crack fault[J].Mechanics in Engineering,2010,32(1)：20-23.

[16]Zhao Xinwei,Luo Jinheng,Yang Zheng,Zhang Hua,zhang Guangli.3-D fracture mechanics characteristics for pipeline steel with surface crack under fatigue load[J].Journal of Mechanical Strength,2009,31(4)：654-660.(In Chinese)

[17]Qi Guiying.Study on 3D-fracture behavior in CTS-specimen with inclined crack[D].Dissertation for the Degree of D. Engineering,Harbin Engineering University,2011：46-47.

疲劳载荷作用下焊接点三维线弹性弯曲裂纹路径预测

杨大鹏1，2，潘海洋3，赵耀2，李天匀2
（1.郑州职业技术学院机械工程系，郑州450121；2.华中科技大学船舶与海洋工程学院，武汉430074；3.郑州职业技术学院城市轨道交通系，郑州450121）

利用二阶摄动方法研究了疲劳载荷作用下结构线弹性裂纹的弯曲扩展问题并求解了三维动态应力强度因子。利用二阶摄动方法研究了疲劳载荷作用下裂纹路径预测时的应力准则与能量准则之间的关系。就均匀物质而言，在二阶摄动分析理论的框架内，两种准则指明了相同的三维疲劳弯曲裂纹扩展路径。但在具有非均匀断裂韧度的物质中，能量准则优越于应力准则。作为二阶摄动方法的实际运用，研究了焊接结构中疲劳线弹性裂纹的形态特征和弯曲扩展路径问题，综合考虑了诸如远场动态作用应力、焊接残余应力、局部物质衰变以及不同尺寸的缺陷的存在等因素，绘制出疲劳载荷作用下退化区域中裂纹弯曲扩展的临界轨迹曲线。

三维疲劳应力强度因子；弯曲裂纹；二阶摄动方法；疲劳能量释放率

O343

：A

杨大鹏（1974－），男，博士，郑州职业技术学院副教授；

1007-7294（2017）03-0318-11

O343

：A

10.3969/j.issn.1007-7294.2017.03.007

潘海洋（1986-），男，郑州职业技术学院助教；

赵耀（1958-），男，华中科技大学教授，博士生导师

李天匀（1969-），男，华中科技大学教授，博士生导师。

Received date：2016-09-23

Foundation item：Supported by Henan Province Basic and Advanced Technology Research Plan Project (No.152300410003);The Training Program of the Major Research Plan of the National Natural Science Foundation of China(No.91016026)

Biography：YANG Da-peng(1974-),male,Ph.D.,associate professor,E-mail：ydpzpysh@163.com;

PAN Hai-yang(1986-),male,assistant.