Modal Pole Placement for Coupled Structural Acoustic System Based on Reduced Order Model
YU Dan-zhu,LI Sheng,2
(1.State Key Laboratory of Structural Analysis for Industrial Equipment,School of Naval Architecture,Faculty of Vehicle Engineering and Mechanics,Dalian University of Technology,Dalian 116024,China;2.Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration,Shanghai 200240,China)
于丹竹1,黎胜1,2
(1.大连理工大学工业装备结构分析国家重点实验室运载工程与力学学部船舶工程学院,辽宁大连116024;2.高新船舶与深海开发装备协同创新中心,上海200240)
Modal Pole Placement for Coupled Structural Acoustic System Based on Reduced Order Model
YU Dan-zhu1,LI Sheng1,2
(1.State Key Laboratory of Structural Analysis for Industrial Equipment,School of Naval Architecture,Faculty of Vehicle Engineering and Mechanics,Dalian University of Technology,Dalian 116024,China;2.Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration,Shanghai 200240,China)
The problem of modal pole assignment of a coupled structural acoustic system based on reduced order model from the forced responses is addressed.The reduced order model might be obtained entirely from measured vibration data,there being no need to determine or to know the structural matrices and the acoustic impedance matrix.The modal natural frequencies and damping ratios of the coupled system are assigned separately and simultaneously using output feedback control by collocated actuator-sensor arrangements.Different control configurations are discussed and active structural acoustic control is demonstrated numerically using a fluid-loaded plate.The numerical examples show that the chosen eigenvalues may be assigned to predetermined values.
pole placement;reduced order model;acoustic fluid-structure interaction; output feedback;active structural acoustic control
0 Introduction
There are many areas of engineering in which fluid-structure coupling is an important issue,with regard to both the sound radiated into the fluid and the effect of the fluid on the vibrations of the structures.Examples include the study of interior noise in automotive,aerospace, and marine vehicles,and the effect of heavy external fluid loading on marine structures.For a coupled structural acoustic problem,such as an acoustic fluid-structure interaction problem[1], the fluid,accelerated and compressed by the vibrating structure,exerts radiation loading,i.e., oscillatory surface pressures that combine with the applied loads,thereby modifying the structural response.Therefore,the effect of fluid-structure interaction has to be included in the coupled structural acoustic system.What is more,the heavy fluid loading is frequency dependent[2]and this makes the determination of the fluid-loaded modes and the corresponding modal control more difficult.In 2006,Li and Li[3]used a matrix-free formulation of rational Krylov projection to construct Reduced Order Models(ROM)and then estimate modal parameters of the fluid-loaded structures from forced responses.The frequency dependence of the acousticimpedance matrix in the coupled structural acoustic system is automatically removed,and there is no need to determine or to know the structural M,C,K matrices and the acoustic impedance matrix.
The problem of pole placement has received considerable attention from the active-control and vibrations communities over several decades[4].The pole placement is about to set natural frequencies and damping to specified values and the applications include the avoidance of large-amplitude vibrations close to resonance,and the design of adaptive structures,capable of changing their behavior to respond in a desirable way to a varying demand[5].The wellknown Independent Modal Space Control(IMSC)method,proposed by Meirovitch in the 1980s[6],is a modal pole assignment method and allows the frequency and damping of the controlled modes to be changed independently using diagonal control gain matrices.Starting from the original IMSC,many improvements were developed to improve its performance and robustness[7].In 2007,a pole assignment approach based on measured receptances to eigenvalue assignment in structural vibration problems was introduced by Ram and Mottershead[8]and became known as the‘receptance method’.The receptance method is very different from previous pole assignment method in a way that it does not require evaluation or knowledge of the system matrices M,C,K.
For the active modal control of structural vibration and sound radiation of fluid-loaded structures,Fein et al[9]presented a modal state-space formulation for a fluid-loaded plate and considered active vibration control of the fluid-loaded plate by means of a modal concept using piezoelectric actuators/sensors.They obtained the modal parameters for the fluid-loaded structure from experimental modal analysis and conducted experiments to verify the active modal control.Li[10]presented an active modal damping control of a fluid-loaded plate via negative velocity feedback,and the feedback gain between the piezoelectric actuators/sensors for the modal control is obtained by using the in-vacuo modal matrix and the incompressible fluid-loaded modal matrix.So far very few reports have concerned with the pole assignment of coupled structural acoustic systems.
This paper presents a pole assignment approach for coupled structural acoustic systems. The approach makes use of Li and Li’s method[3]for modal pole placement,the advantage is even if the explicit system matrix form is not available,the ROM can still be constructed directly from transfer functions by experimental measurements.The problem of assigning the poles of the system to predetermined values is then solved by choosing the appropriate feedback gain matrix.The present method is demonstrated by means of a numerical example of active control of structural vibration and acoustic radiation of a plate underwater.
1 Theory
1.1 Coupled structural acoustic model
For structures with fluid-loading,based on the well-established coupled finite element and boundary element analysis,the matrix equation of motion is given by[11],


The link between the acoustic pressure and the velocity distribution on the surface of the structure can be always written as[3],

where Z denotes the acoustic impedance matrix and vnthe vector of the surface normal velocity.For acoustic radiation problems,Z in general being complex-valued and frequency dependent,could be obtained by boundary element method for an arbitrary shaped three-dimensional bodies or by the surface Rayleigh integral for a baffled plate.
The normal velocity vector vnis related to the structural velocity vector v and the vector of the structural displacement x through the transformation matrix G,

Substituting Eqs.(2)and(3)into Eq.(1)yields,

where contains the structural displacement vector x as the only unknown variable to describe the coupled structural acoustic system.
1.2 Active control of coupled structural acoustic system
Consider the active control problem below,

where the vector Ffrepresents the control force derived from the action of a set of force actuators represented by,

where the m×1 vector u denotes the m inputs,one for each control device(actuator),and Bfdenotes the nd×m matrix of weighting factors,(influence coefficients)or actuator gains,ndis the total number of structural degrees of freedom(DOF).
In order to control the system,we need a feedback loop.Let y be an s×1 vector of sensor outputs denoted and defined by,

where Cdand Cvare s×ndmatrices of displacement and velocity influence coefficients,respectively.The output is feedback to the input vector u of the actuator array in the form,

where the m×s matrix Gfconsists of constant feedback gains.
In the way above,the active control problem is then reduced to the modified form,
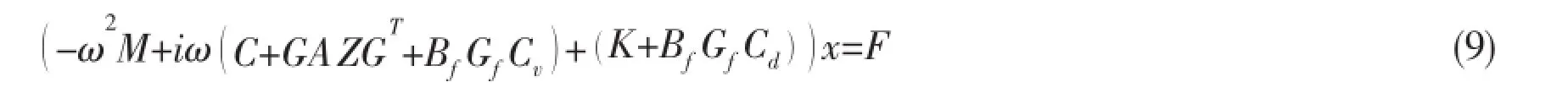
The pole placement in the such way is equivalent to find suitable control matrix to realize the desirable eigenvalue distribution.
2.3 Modal parameter estimation by ROM using transfer function
The receptance matrix,which is measurable experimentally,is the inverse of the dynamic stiffness matrix.The receptance matrix H()ωof the open-loop coupled system is now defined as,

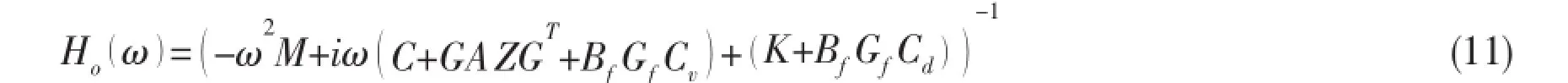
To identify the modal parameter of the coupled structural acoustic system from the measured transfer function,we use the reduced order model[3],which is based on rational Krylov projection.First introduce a transfer function,

Any other transfer function can also be used as soon as it captures the dynamics of the coupled system.System matrices of the ROM are derived from the above transfer functions at a set of interpolation frequencies,theα,()βblock of the stiffness and mass matrices of the ROM is given by,


2.4 Modal pole assignment[12]
To cause the closed-loop system to have the desired poles(eigenvalues)and,hence,a desired response,the Bf,Cd,Cvand Gfmust be chosen appropriately.When the velocity feedback is used,the choice of the gain is through the equation
When the displacement feedback is used,the choice of the gain is through the equation
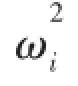
2.5 Active control simulation and vibro-acoustic response
For a fluid-loaded structure and a Multiple-Input-Multiple-Output(MIMO)control system using displacement/velocity feedback,if the actuator and sensor locations are chosen,then the input matrix Bf,the output displacement matrix Cdand the output velocity matrix Cvare known,the pole assignment problem is to solve gain Gffrom Eq.(16)and Eq.(17)to get desired modal response information.Once Gfis chosen appropriately,the eigenvalues of the controlled system and the corresponding vibro-acoustic response x,vnand p are determined.Further,the acoustic power Π radiated from the structure can be calculated as,

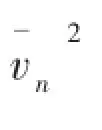

where S0is the area of the structure surface.
3 Numerical examples
The dimensions of a simply supported plate in a baffle are Lx=0.455 m,Ly=0.379 m,and thickness h=0.003 m.The plate is made of steel with density ρs=7 850 kg/m3,Young’s modulus E=2.1×1011N/m2,and Poison’s ratio v=0.3.The disturbance is assumed to be a point force with amplitude F0=1 N and located at the plate center.The plate is assumed to be vi-brating in water with a density ρ=1 000 kg/m3and a sound speed c=1 500 m/s.The proportional damping coefficient α=7.522 7 and β=1.136 42×10-5.The plate is modeled by 16×16 four-noded quadrilateral isoparametric elements and the element mesh is shown in Fig.1.The finite element is based on the Mindlin plate theory(the first-order shear deformation theory). The Rayleigh integral on the plate surface is calculated by discretisizing the plate surface with the same mesh as the plate finite element mesh.The total number of structural DOFs is nd=803.Twelve evenly distributed interpolation frequencies in the frequency band(10,560)Hz and force matrix consisting of five probing vectors are used to obtain the transfer functions and construct the ROM.
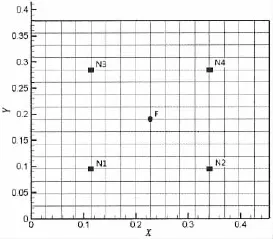
Fig.1 Plate element mesh and collocated sensor/actuator locations
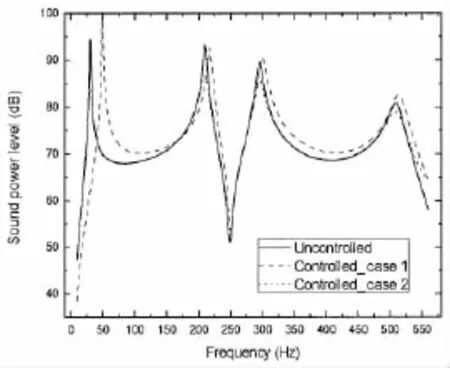
Fig.2 Sound power level before and after control for Case1 and Case 2
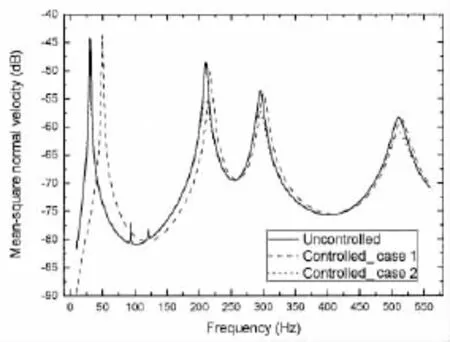
Fig.3 Mean-square normal velocity level before and after control for Case 1 and Case 2

Fig.4 Sound power level before and after control for Case 3 and Case 4
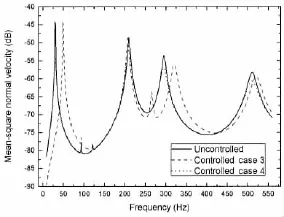
Fig.5 Mean-square normal velocity level before and after control for Case 3 and Case 4
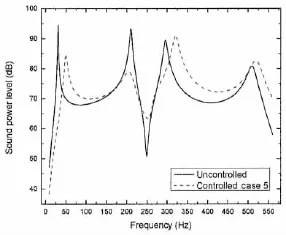
Fig.6 Sound power level before and after control for Case 5
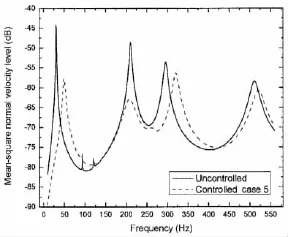
Fig.7 Mean-square normal velocity level before and after control for Case 5
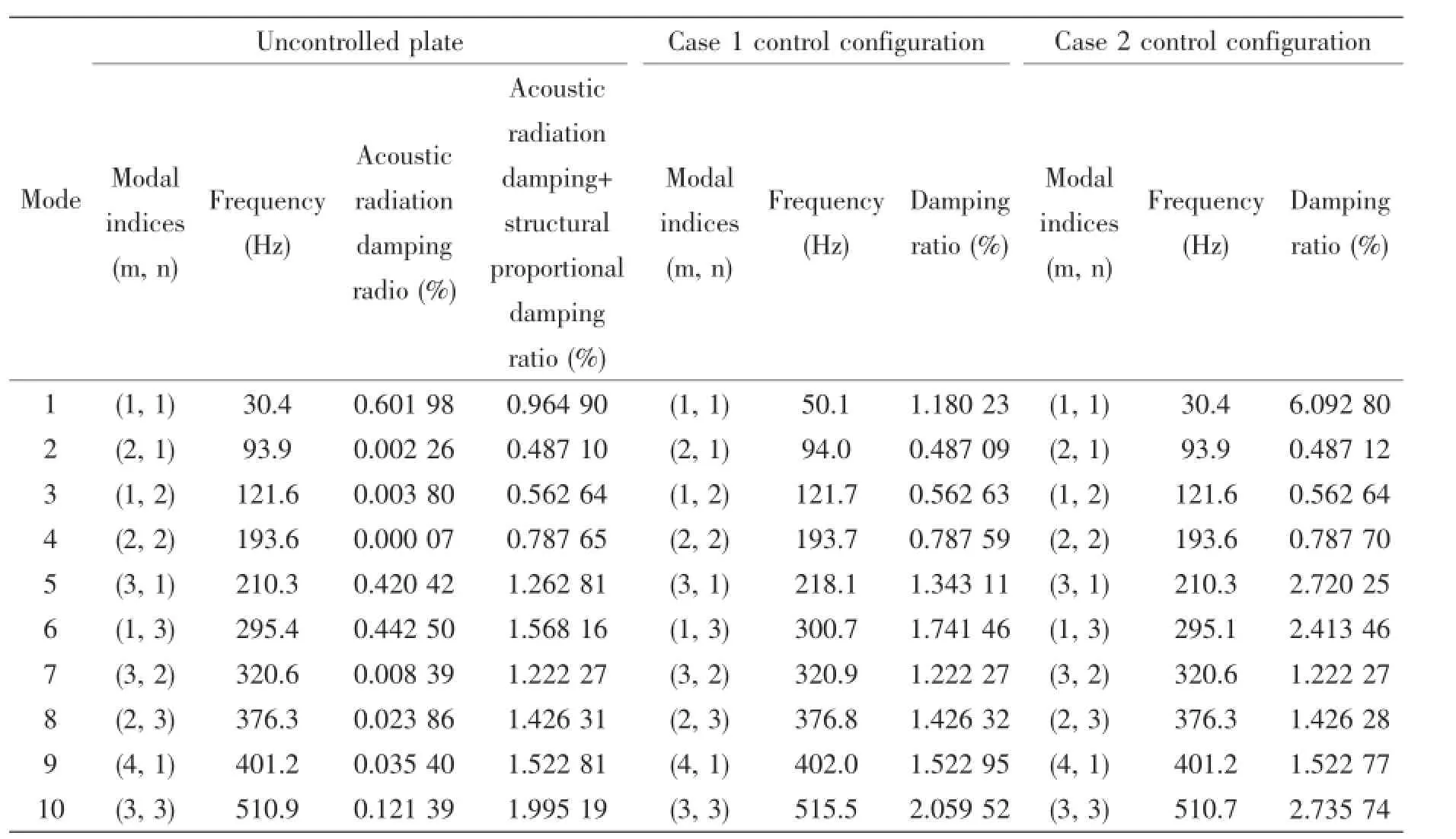
Tab.1 Natural frequencies and modal damping rations of the plate before and after control for Case 1 and Case 2
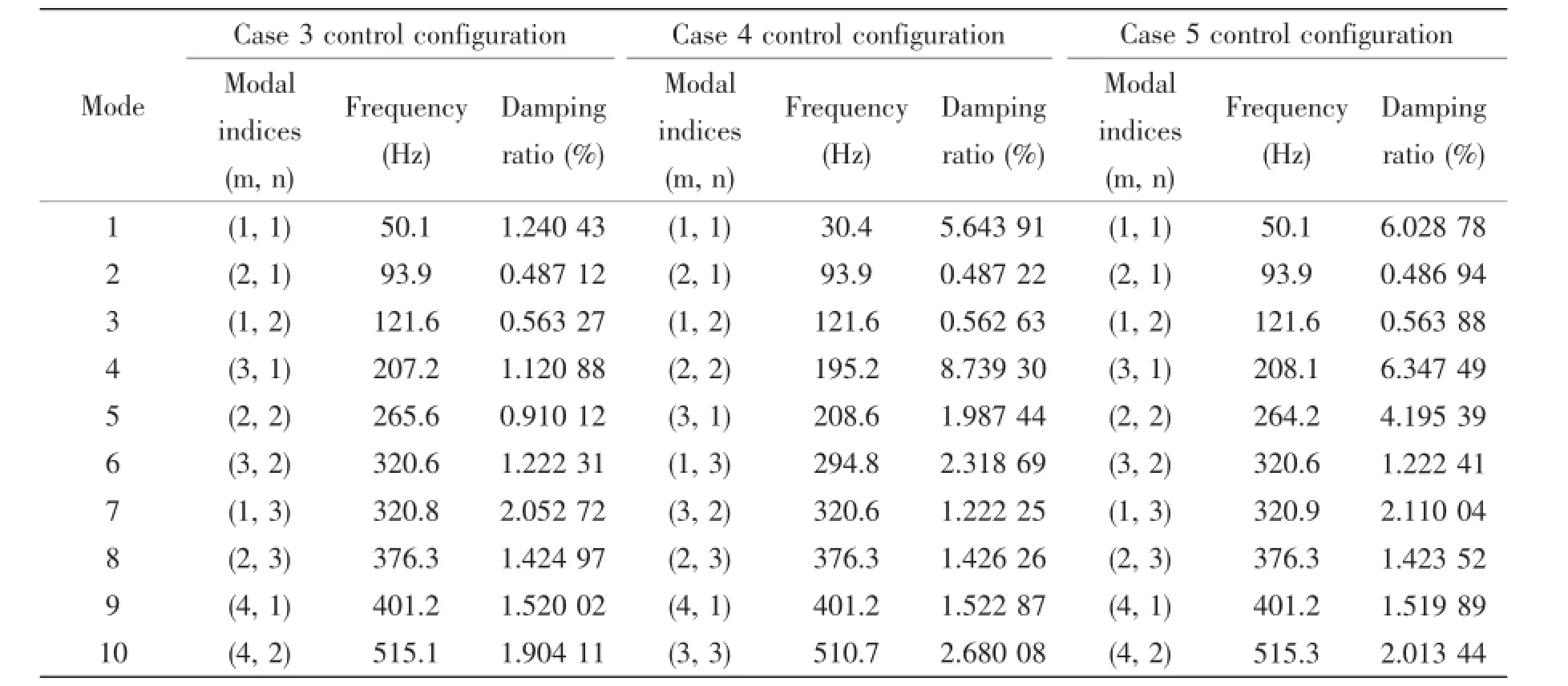
Tab.2 Natural frequencies and modal damping rations of the plate after control for Case 3,Case 4 and Case 5
Figs.2-7 show the sound power level(dB,re:10-12W)and the mean-square normal velocity level(dB,re:1 m2/s2)of the plate without and with control for all cases of the five different control configurations,the numerical results are obtained by a frequency sweep with increments of 1 Hz.The first 10 natural frequencies and modal damping ratios of the plate without and with control for all cases are listed in Tab.1 and Tab.2.
From the figures and tables,we can see that for Case 1,the first-mode natural frequency is changed from 30.4 Hz to 50.1 Hz,the sound power level at 30 Hz is reduced from 94 dB to 61 dB.For Case 2,the first-mode damping ratio is changed from 0.964 90%to 6.092 80%, the sound power level at 30 Hz is reduced from 94 dB to 84 dB.For Case 3,the first-mode natural frequency is changed from 30.4 Hz to 50.1 Hz,the sound power level at 30 Hz is reduced from 94 dB to 61 dB.For Case 4,the first-mode damping ratio is changed from 0.964 90%to 5.643 91%,the sound power level at 30 Hz is reduced from 94 dB to 84 dB.For Case 5,the first-mode natural frequency and damping ratio are changed simultaneously to 50.1 Hz and 6. 028 78%,the sound power level at 30 Hz is reduced from 94 dB to 61 dB,at the assigned resonant frequency 50 Hz the sound power level is 85 dB which is less than 94 dB.To see the control performance on sound pressure at field points,Fig.8 shows the sound pressure level(dB,re:10-6Pa)at a field point(0.24 m,0.15 m,1.50 m).We can see that the effects of active control on the field pressure are similar as on the sound power.
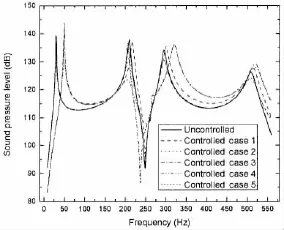
Fig.8 Sound pressure level before and after control

Fig.9 Mode shapes of Modes 1,4,5,and 7 of control configuration Case 3
It is clear that the realizations of the eigenvalue assignment are achieved.However,we also can see that the controls on the first mode affect uncontrolled modes,especially in Case 3,Case 4 and Case 5.As we know,if the mass matrix,the stiffness matrix and the damping matrix can be diagonalized by the modal matrix,independent modal control can be achieved. For a fluid-loaded structure,to whatever degree that these conditions are hard to exactly meet since the heavy fluid loading is frequency dependent and the fluid-loaded modes are complex modes.In addition,the active control especially the actuator locations also affect the mode shapes(modal matrix).From Tab.2,we can see from the modal indices(m,n)that the modal order of Case 3 and Case 5 is different from that of uncontrolled plate.Fig.9 illustrates the mode shapes of Modes 1,4,5,and 7 of control configuration Case 3.It is clear that the controlled water-loaded shapes display big perturbations of the conventional mode shapes of the plate with Modal indices(1,1),(3,1),(2,2)and(1,3),respectively.To avoid the side effects of the above control strategy,what we can do is to have a control only in the working frequency range such as in a narrow band around 30 Hz,the design of a practical feedback control system thus generally involves a compromise between having a high control gain to achieve good performance in the working frequency range,and having a lower control gain to avoidside effects on other modes outside the working frequency range.
4 Conclusions
In this paper,a transfer function which might be obtained from measurements is used to construct the ROM of a coupled structural acoustic system,the problem of assigning the poles of the coupled system to predetermined values is then solved by choosing the appropriate feedback gain matrix.The method is demonstrated by means of a numerical example of active control of structural vibration and acoustic radiation of a plate with different control configurations.Numerical results of water-loaded natural frequencies and damping ratios,radiated sound power,mean-square normal velocity and field pressure of the plate with and without control show that the realizations of the eigenvalue assignment are achieved.
[1]Junger M C.Acoustic fluid-elastic structure interactions:Basic concepts[J].Computers&Structures,1997,65(3):287-293.
[2]Giordano J A,Koopmann G H.State-space boundary element-finite element coupling for fluid-structure interaction analysis[J].Journal of the Acoustical Society of America,1995,98:363-372.
[3]Li X,Li S.Modal parameters estimation for fluid-loaded structures from reduced order models[J].Journal of the Acoustical Society of America,2006,120:1996-2003.
[4]Wei X,Mottershead J E,Ram Y M.Partial pole placement by feedback control with inaccessible degrees of freedom[J]. Mechanical Systems and Signal Processing,2016,70-71:334-344.
[5]Tehrani M G,Elliott R N R,Mottershead J E.Partial pole placement in structures by the method of receptances:Theory and experiments[J].Journal of Sound and Vibration,2010,329(24):5017-5035.
[6]Meirovitch L.Dynamics and control of structures[M].New York:John Wiley and Sons,1990.
[7]Serra M,Resta F,Ripamonti F.Dependent modal space control[J].Smart Materials&Structures,2013,22(10):622-629.
[8]Ram Y M,Mottershead J E.Receptance method in active vibration control[J].AIAA Journal,2007,45(3):562-567.
[9]Fein O M,Gaul L,Stobener U.Vibration reduction of a fluid-loaded plate by modal control[J].Journal of Intelligent Material Systems and Structures,2005,16:541-552.
[10]Li S.Active modal control simulation of vibro-acoustic response of a fluid-loaded plate[J].Journal of Sound and Vibration,2011,330(23):5545-5557.
[11]Everstine G C,Henderson F M.Coupled finite element/boundary element approach for fluid-structure interaction[J].Journal of the Acoustical Society of America,1990,87:1938-1947.
[12]Inman D J.Vibration,with control,measurement and stability[M].Englewood Cliffs,New Jersey:Prentice Hall,1989.
于丹竹1,黎胜1,2
(1.大连理工大学工业装备结构分析国家重点实验室运载工程与力学学部船舶工程学院,辽宁大连116024;2.高新船舶与深海开发装备协同创新中心,上海200240)
摘要:基于结构声耦合系统的降阶模型实现了水下结构振动和声辐射的极点配置。文中的降阶模型可完全基于结构声耦合系统的振动响应通过实验来获取,可以不需要形成或知道结构的质量阵、阻尼阵、刚度阵和流体的声阻抗矩阵。以水中板结构的振动和声辐射为例使用同位的传感器/作动器布置采用输出反馈控制对流体加载下的板的固有频率和阻尼进行了配置,并对不同的控制构型进行了分析和讨论。数值模拟结果表明基于降阶模型进行水下结构振动和声辐射的极点配置是可行的。
基于降阶模型的结构声耦合系统的极点配置
极点配置;降阶模型;流固耦合;输出反馈;结构声主动控制
TB53
:A
于丹竹(1985-),女,大连理工大学船舶工程学院博士研究生;
1007-7294(2017)03-0361-11
TB53
:A
10.3969/j.issn.1007-7294.2017.03.011
黎胜(1973-),男,大连理工大学船舶工程学院教授,博士生导师。
Received date:2016-09-27
Foundation item:Supported by the Funds of Science and Technology on Underwater Test and Control Laboratory under Grant No.9140C260101130C26095
Biography:YU Dan-zhu(1985-),female,Ph.D.student;
LI Sheng(1973-),male,professor/tutor,E-mail:shengli@dlut.edu.cn.
- 船舶力学的其它文章
- Numerical Study on the Nonlinear Characteristics of Longitudinal Motions and Wave Loads for SWATH Ship in Regular Head Waves
- Coupled Hydrodynamic and Aerodynamic Response Analysis of a Tension-Leg Platform Floating Wind Turbine
- Validation of CFD Simulation for Ship Roll Damping
- Motion Behavior of a Semisubmersible in Freak Waves
- Numerical Investigation of the Side Wall Effects for Two Ship Models Advancing Parallel in Waves
- Three-Dimensional Problem of the Compressible Water-gas Mixture Impacting on Rigid Plates

