Numerical Investigation of the Side Wall Effects for Two Ship Models Advancing Parallel in Waves

XIAO Wen-bin

(Academy of Ocean Science and Technology,National University of Defense Technology,Changsha 410073,China)

Numerical Investigation of the Side Wall Effects for Two Ship Models Advancing Parallel in Waves

XIAO Wen-bin

(Academy of Ocean Science and Technology,National University of Defense Technology,Changsha 410073,China)

A three-dimensional(3-D)Green function method,as the translating-pulsating source in frequency domain as its kernel,is developed to investigate the side wall effects for two ship models advancing parallel in the regular waves of towing tank.Distributed source integration approach is applied to solve the wave exciting forces and free motions of the two models in close proximity.Satisfaction of the impenetrable boundary condition of tank walls is achieved by the mirror image principle,as a result of the tank-wall Green function representation including an infinite series.From the propagation characteristics of a point source in far field,it is obvious that all kinds of wave patterns are not possible to emerge ahead of the source if Strouhal number is larger than 0.272 and the influence scope of propagating waves can then be defined by the half angle of ring-fan wave.Different from the side wall effects for single ship model,the interference of the reflection waves from the tank walls acting on both ships has to be taken into consideration.According to the ship particulars, tank breadth and relative position of two ships,a discriminant method is proposed for two models by six geometric critical half angles.For the sake of simplifying tank-wall Green function,mirrored images of point source and ship model are discussed to acquire the approximate mirror number.The quantitative differences of tank-wall Green function at different mirror numbers involve the area aft of ship bow.Based on the principles of integral efficiency and accuracy,finite terms of the infinite series can be selected for the tank-wall Green function.Numerical results show that the impact of the side wall effects on the two-ship motion responses is focused on the long-wave tested conditions.

two ships;side wall effects;Green function method; translating-pulsating source;model test

0 Introduction

In the towing tank with finite breadth,side wall effects may exert great influence on the ship model advancing in waves,which are mainly due to the reflection waves acting on the model.The waves produced by the model propagate toward the side walls of the tank,and then may go back to it.If there are side wall effects,many experimental results,such as the free motions,wave exciting force,unsteady wave pattern and fluctuating pressure,may be affected.Studies about these effects will contribute to the investigation of hydrodynamic performance difference in the open water and towing tank conditions[1],and qualitative and quantitative analyses are expected for the side wall effects in seakeeping model test.

The model tests of two ships advancing parallel in waves now are still not sufficient for technological complexity in engineering.The main difficulties are as follows：(1)Different from the normal tank,the towing carriage for two-model test should be equipped with another auxiliary towing apparatus[2],which may add to the experimental cost.(2)The longitudinal and vertical motions are given great attention for the advancing single model in head waves.However,the freedoms of two-model roll motions should be released for the non-ignorable transversal disturbance.(3)The transversal distance between two models should be adjustable according to different test conditions.The enlargement of transversal distance may intensify the side wall effects,which makes two-model tests more difficult in the experimental design and data analysis.For the single floating body,the 15th International Towing Tank Conference proposed a standard for seakeeping experiment in the form of check list[3].Based on the ITTC standard, the side wall effects were considered and checked in the two-model tests by Yang[4]and Mc-Taggart,et al[5],which both neglect the mutual interaction of the two models in close proximity.It must be recognized that the side wall effects are much complicated for two advancing models.Except for the critical wavelength corresponding to each model,the radiation and diffraction waves generated by a model may act upon another one.Additionally,the relative position of two models in the towing tank should be taken into account whether the tank wall effects occur in waves.

For the side-wall effects problem in waves,the theories and computational methods have developed recently from the 2-D approximate approach to the 3-D boundary element method. Earlier studies were oriented toward the qualitative analysis of side wall effects by the thin ship theory[6]and strip theory[7-9].The 3-D panel method was firstly proposed by Kashiwagi (1989)to investigate the side wall effects and the hydrodynamic calculations were carried out for the zero-speed[10]and forward-speed[11]cases,in which the numerical results agreed well with the test data of a prolate spheroid and a Lewis-form ship model.The pioneering works by Kashiwagi push forward the quantitative calculations of the side wall effects for single floating body.From the radiation problem only,unsteady wave measurement was introduced to the side wall effects by Iwashita,et al[12]and their calculated results of a panel method in time domain were validated by model experiment.

In present paper,3-D Green function method with the integral kernel of translating-pulsating source in frequency domain has been employed to probe into the side wall effects of two ship models.Based on the propagation characteristics of this kind of Green function,a practical approach is proposed to discriminate the side wall effects for two models in close proximity.The influences of side wall effects on the wave exciting forces and free motions are illustrated by the two-model test example.

1 Basic mathematical problems

1.1 Definite conditions of flow velocity potentials

A right-hand Cartesian coordinate system o-xyz,as shown in Fig.1,is defined by placing the o-xy plane coinciding with the undisturbed free surface and oz axis oriented positively upward.The origin o is set at the axial plane of the tank and the coordinate system is moving with the same speed as the models.In the towing tank with the breadth BT, two ship models,numbered as a and b,are assumed to advance at constant forward velocity U and oscillate sinusoidally with frequency ωe.The transversal and longitudinal spaces between two models are denoted by Dxand Dy.For Dx＞0,ship b is ahead of ship a.And for Dy＞0,ship b is on the starboard side of ship a.

The flow liquid is satisfied with the assumption of irrotational and incompressible ideal fluid and the surface-tension effect is ignored here.If the incident wave elevation and ship oscillatory motion are small,the unsteady velocity potential Φ x,y,z,（）t in the first order form can be written below.

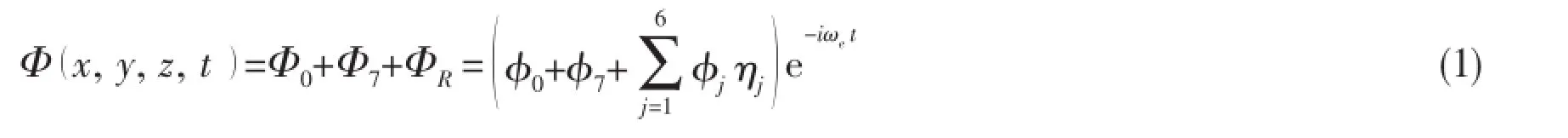
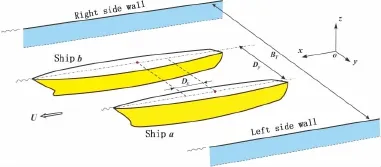
Fig.1 Definition of the coordinate system

where Φ0,Φ7and ΦRare the incident,radiation and diffraction potentials,respectively;φ0and φ7are the spatial components of Φ0and Φ7,respectively;φjis the amplitude of radiation potential at unit oscillatory motion and ηjis the first-order motion at six degree of freedom, where the cases of j=1～6 correspond to surge,sway,heave,roll,pitch and yaw modes.

The velocity potential in the flow field here is not only satisfied with the 3-D Laplace equation,linearized free surface condition,bottom boundary condition and far-field radiation condition,but also the ship surface condition,which can be written as

The boundary conditions of side-wall effects problem are different from those in open water and an extra boundary condition is the impenetrable condition of tank walls,which can be written as

Specifically,the velocity potential φjhere is included with not only the radiation and diffraction potentials under open water,but also the potential contribution of tank-wall reflection.

1.2 Boundary integral equation

By employing the 3-D Green function method,the differential equations in the definite conditions are transformed into the integral equations on the ships’surfaces.Satisfied with the conditions mentioned above,the flow velocity potential can be demonstrated by the reasonable Green-function distribution with the point-source form or the hybrid source-and-dipole form. Here,the velocity potential φjj=1～（）7 is the solution of boundary integral equation with the point-source form,illustrated in Eq.(4).

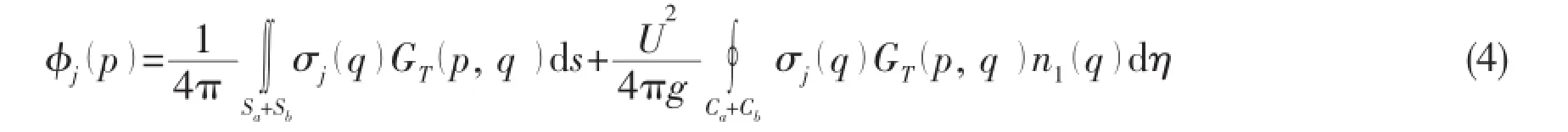
where GT（ p,q） is the tank-wall Green function;q（ ξ,η,ζ）is the source point at the flow field;σ（q） is the unknown source strength;S is the mean wetted surface of the ship body;C is the intersection line of ship surface and undisturbed free surface;n1（q） denotes the unit normal component along the η axis on the water line C.The ship surface is numerically subdivided into hundreds of panels and the source strength is assumed as a constant on each discretized panel.

According to the mirror image principle,tank-wall Green function GTp,（）q can be presented as follows：

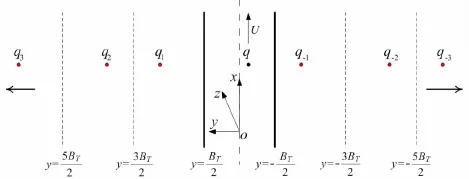
Fig.2 Images of the translating-pulsating source

For the two models advancing in the parallel course,the transversal space between the models’gravity centers is almost one order of the magnitude with the ship length.So,the transversal influence of the translating-pulsating source cannot be negligible at the ship wetted surface by the slender-ship theory,which makes it difficult to calculate the infinite series shown in Eq.(5).If the tank-wall Green function is not simplified,the numerical computation will be very inefficient.

By putting the partial derivatives of Eq.(4)along the normal direction of ship surface into the Eq.(2),the source strength can be numerically solved at each mode.The velocity potential on the ship surface is then determined after the substitution of the known strength into the Eq.(4).

1.3 Wave exciting forces and free motions

By the rigid-body dynamics,the coupled motions of two ship models in waves can be expressed below：

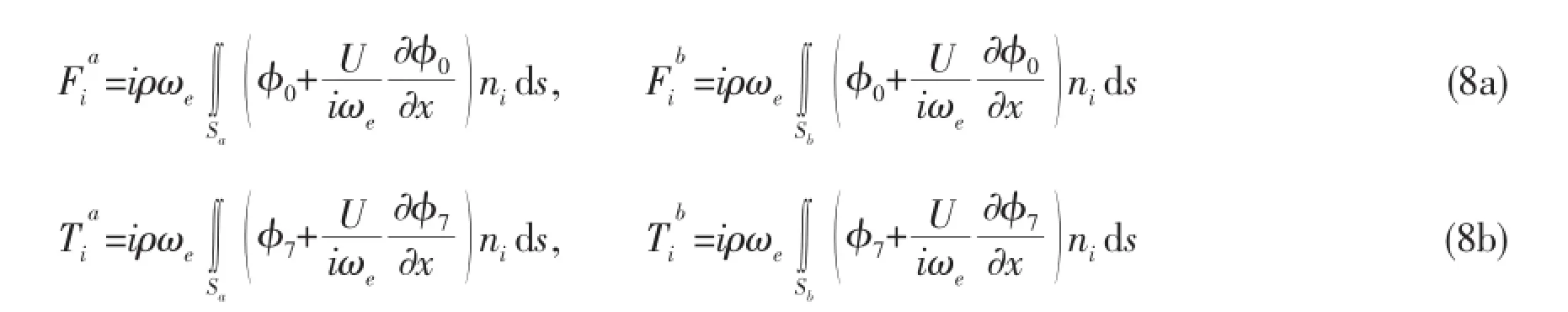
For any ship model,the wave exciting force is defined as the sum of its Froude-Krylovforce and diffraction force.Eq.(7)is composed of twelve coupled equations,whose solutions are the plural motion responses of two models at six degree of freedom.

2 Discrimination of side wall effects for two models

For the tested models,the freedom of free motions are not restricted all.Based on the propagation characteristics of 3-D translating-pulsating source Green function,a discrimination method is here proposed for the side-wall effects problem of two ship models.The cases to discuss are the head incident wave and τ＞0.272.If the distance between the ship a and the left side wall isassumed as Da,six geometric critical half angles,illustrated in Fig.4,can be determined by the ship length,tank breadth and relative position of two models.The detailed representations of the six angles are written as follows：

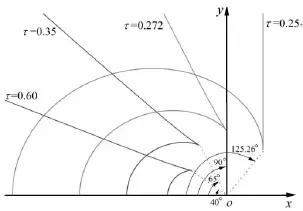
Fig.3 Constant phase curves of ring-fan wave patterns

Fig.4 Six geometric critical half angles

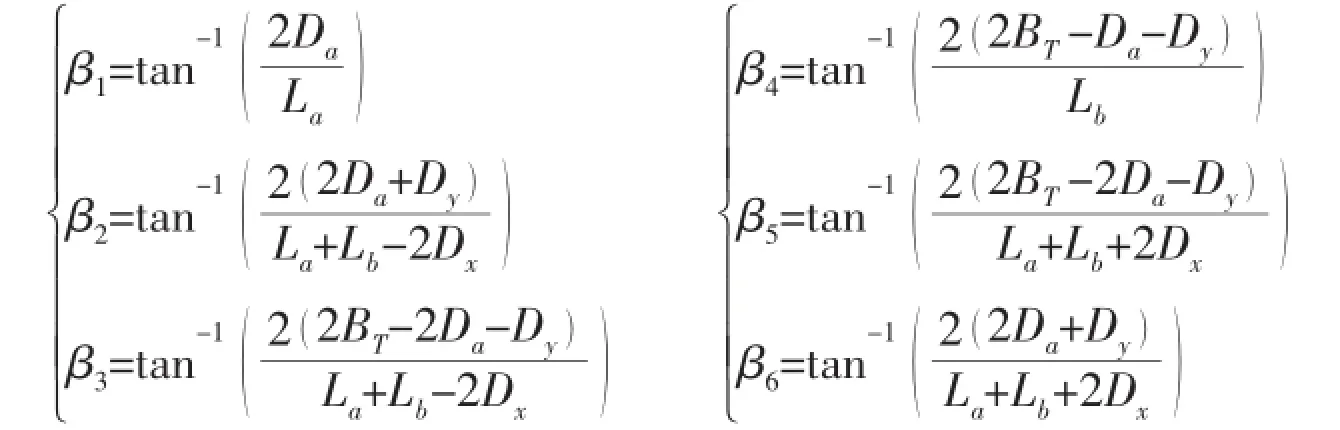
where Laand Lbare the waterline lengths of ship a and ship b,respectively.

In the six geometric critical half angles,β1and β4correspond to the critical cases that the radiation-diffraction waves generated by the ship model reflect back from the side wall and interfere its own motions.If the longitudinal space between two models are large enough,wave patterns related to β1and β4may bypass its original model and act on the other one,where the critical angle should be referenced by β2and β5.Because of the shadowing effect of ship body, the interference waves between the models’sides are restricted in a narrow area.However, the motion responses of any ship model must be affected by this kind of interference waves, that is to say,the interfered model generates new radiation-diffraction waves.If the secondary reflection of the waves between the ships’sides is not taken into account,β3and β6cannot be neglected in the side-wall effects discrimination.Above all,the side wall effects for two ship models advancing parallel in waves can be discriminated by the six geometric critical angles above.The minimum value of these angles is defined as βtto determine whether the side wall effects occur.

If the half angle of the ring-fan wave pattern βrcorrelated to the tested case is larger than the minimum angle βt,the side wall effects will occur.However,these kind of effects do not appear if βr＜βt.

An experiment[22-23]was carried out to measure the surge,heave,roll and pitch motions of two ship models advancing in head regular waves at a towing tank(132 m×10.8 m×2 m).Ship a is placed in the central axis of tank and the longitudinal space between two models is always set as 0 m.The two models are towed respectively by two towing apparatuses in the carriage.Tab.1 shows the main particulars of the tested models.

Tab.1 Main particulars of the tested models

In the test above,forward speeds of the two models are the same and the speed-Froudenumber Fr=0.149,0.171 for ship a.The range of wavelength in head waves is from 2 m to 10 m.By the tested parameters of ship speed and wavelength,the minimum value of Strouhal number τ equals to 0.28,which is larger than 0.272.Therefore,the radiation-diffraction waves produced by the actual and mirrored models are all propagating toward the sterns.By Eq.(9),it can be easy to determine the parameters such as the critical half angle βt,range of tested wavelength λ and Strouhal number τ with the interference of side walls,illustrated in Tab.2.

Tab.2 Cases of the model test if side wall effects are in presence

3 Numerical results and discussion

3.1 Simplified computation of tank-wall Green function

By applying the mirror image principle in the side-wall effects problem,the infinite mirrored models will exert the hydrodynamic interaction on the actual models.However,this kind of interaction decreases as the transversal distance between the mirrored and actual models increases.If the image number m is greater than a certain value,the effective interaction area will shrink and even vanish by the wave-propagation characteristics mentioned in Chap.2.On the basis above,simplified method of the infinite series in Eq.(5)is introduced and the tankwall Green function GTis turned into finite terms.

For the tested models in Tab.1,the origin o in the follow-up coordinate system is fixed on the intersection line of center buttock and middle section of ship a.There is a point source q（ La/2,0,-1） located at the bow of ship a.Fig.5 and Fig.6 illustrate how the tank-wall Green function changes along the lengthwise direction of ship a,where the image number m=1,3,7, 15.

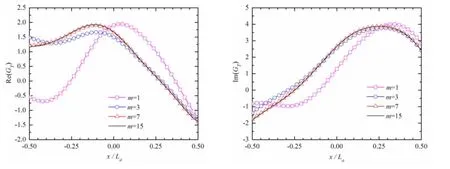
Fig.5 Dependence of Re GT（）and Im GT（）on the image number m(τ=0.28,Fn=0.149,λ=10 m)

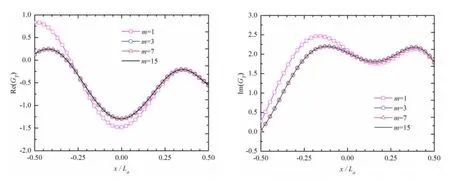
Fig.6 Dependence of Re GT（）and Im GT（）on the image number m(τ=0.295,Fn=0.149,λ=9 m)

As seen in Fig.5,the magnitude differences of tank-wall Green function are getting smaller and smaller with the increase of image number.The curve of Green function with m=7 is almost coincided with that with m=15,which indicates that the propagating waves of mirror images pose little impact to the ship a if m≥7.In the Fig.6,the real part and imaginary part of tank-wall Green function with m=3 are fundamentally the same as those with m=7,15.The common trait in the two figures above is that the magnitude difference in the vicinity of ship stern is greater than that around the ship stem,which is related to the wave backward-propagating characteristic for τ＞0.272.

3.2 Wave exciting forces

From the analysis in Section 3.1,there are certain differences of tank-wall Green function at different image numbers.In the experimental condition,measured data are generally in the macroscopic quantity such as wave exciting force or free motions of ship model.Therefore, the integral results of tank-wall Green function and its partial derivatives on ship wetted surface are needed to be taken into account for the side-wall effects problem.

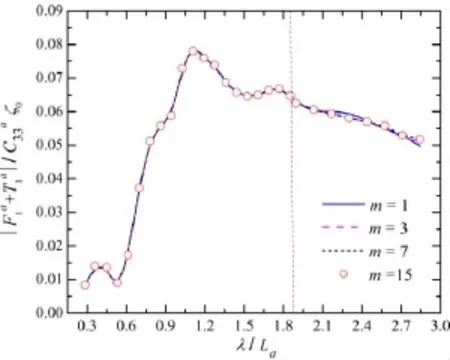
Fig.7 Dependence of the surge wave load of ship a on the image number

Fig.8 Dependence of the sway wave load of ship a on the image number

As the integral kernel of simplified tank-wall Green function,3-D panel method is applied to determine the wave exciting forces of the two models with the experimental conditions of advancing speed,relative position and wavelength.Figs.7-12 depict the calculated resultsof wave loads of ship a in the condition of Fr=0.149 and Dy=0.35La,in which ζ0is the amplitude value of the incident wave.As seen in these figures,the differences of wave exciting forces mainly occur near the maximum wavelength if m=3,7.However,the results of wave loads are almost coincided if m=7,15.Therefore,the image number of seakeeping calculation should be set to 7 at least in this test,that is to say,the numerical calculation can meet the engineering accuracy requirement with 7 mirrored models on each side of the actual model in the side-wall effects problem of the two models here.

Fig.9 Dependence of the heave wave load of ship a on the image number

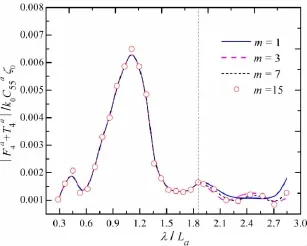
Fig.10 Dependence of the roll wave load of ship a on the image number

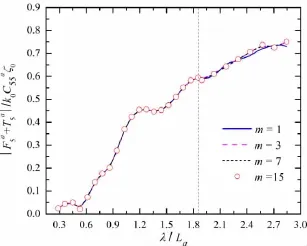
Fig.11 Dependence of the pitch wave load of ship a on the image number

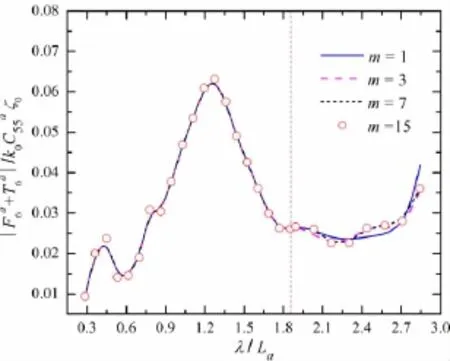
Fig.12 Dependence of the yaw wave load of ship a on the image number

3.3 Free motions

By the translating-pulsating source Green function in the open water,validation had been performed through the free motions of ship a and ship b by Xu&Dong[22-23],in which the calculated results agreed well with those of tests.For the side-wall effects problem,the detailed test data are not listed and the great attention is focused on the numerical algorithm and the quantitative analysis in present paper.

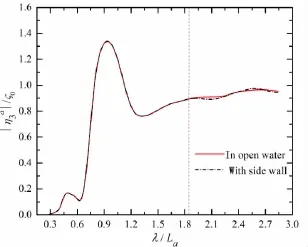
Fig.13 Side wall effects on the heave motion of ship a

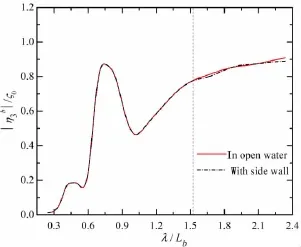
Fig.14 Side wall effects on the heave motion of ship b

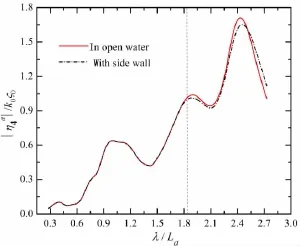
Fig.15 Side wall effects on the roll motion of ship a

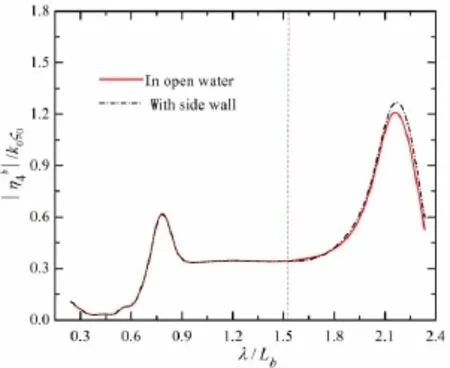
Fig.16 Side wall effects on the roll motion of ship b

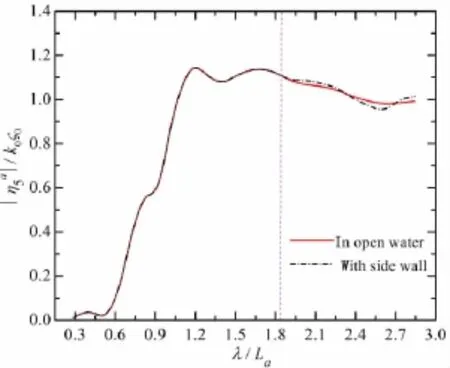
Fig.17 Side wall effects on the pitch motion of ship a

Fig.18 Side wall effects on the pitch motion of ship b

By using the 3-D panel method mentioned in Section 3.2,the numerical results of motion responses considering the side wall effects are compared with those excluding these effects,which are illustrated in Figs.13-18 in the tested condition of m=7,Fr=0.149 and Dy= 0.35La.From the figures below,the main conclusions can be drawn as follows：(1)If the wavelength is less than 6.59 m(corresponding to λ/La≤1.81),the models’motions by the tankwall Green function fit well with those in the water with an infinite free-surface extent.(2)If λ＞6.59 m,the side wall effects occur for the two advancing models,which indicates that λ=6.59 m is the critical wavelength here.The critical wavelength above is consistent with that in Tab.2,which validates the availability and applicability of the discrimination method presented as Eq.(9).(3)Although the side wall effects occur in this test,the numerical calculations show that the intensity of tank-wall interference is small.In comparison with the results by the 3-D Green function in open water,variations of motion amplitudes are all less than 4%with side wall effects accounted.For Fr=0.171,the influence of side wall effects on the ship dynamic motions seems to be even small at three transversal spaces.Above all,the side wall effects are in presence for this two-model seakeeping test but their influence is relatively small to the hydrodynamic performance of the two advancing ships in close proximity.

4 Conclusions

(1)Based on the translating-pulsating source Green function in frequency domain,the 3-D panel method is proposed to effectively describe the side wall effects,in which the Laplace equation,linearized free surface condition,bottom boundary condition,far-field radiation condition,ship surface condition and the impenetrability of side walls are taken into account in the definite conditions.By the mirror image principle,the representation of tank-wall Green function is derived in the form of Green function in open water and an infinite series about the mirror images.

(2)For the point source,the wave systems and their characteristics are discussed at different Strouhal numbers.If the Strouhal number τ is greater than 0.25,the influence scope of the ring-fan wave pattern can be regarded as the propagating area of the radiation-diffraction waves generated by the translating-pulsating source.By the ship particulars,tank breadth and relative position of two ship models,the interference is accounted for the tank-wall reflection of the radiation-diffraction waves to both models.Six geometric critical half angles are developed to represent the complex waves produced by the two advancing models and a practical discrimination method is proposed to exam the side wall effects.

(3)The mirrored models exert the confined hydrodynamic interaction on the actual models along with the increase of image number.By an appropriate image number,the infinite series in the tank-wall Green function can be simplified and the numerical computation will be much efficient.As the simplified tank-wall Green function as the integral kernel,the wave exciting forces and free motions of two models are calculated numerically and the influence of side wall effects can be explored in magnitude for the tested seakeeping example.

[1]Tasai F,Takaki M,Ohkusu M.Ship motions in restricted waters[J].Journal of the Japan Society of Naval Architects and Ocean Engineers,1978,56：33-45.

[2]Evert L,Marc V,Guillaume D.Captive model testing for ship to ship operations[C].Proceedings of International Conference on Marine Simulation and Ship Maneuverability,2009：1-10.

[3]Seakeeping Committee of ITTC.Report of the seakeeping committee[C].Proceedings of the 15th International Towing Tank Conference,1978：55-114.

[4]Yang W H.Experimental verification of the seakeeping performance for two ships advancing parallel in waves[D].Master Thesis of National Cheng Kung University,Taiwan ROC,2002.

[5]McTaggart K,Cumming D,Hsiung C C.Seakeeping of two ships in close proximity[J].Ocean Engineering,2003,30：1051-1063.

[6]Hanaoka T.On the side-wall effects on the ship motions among waves in a canal[J].Journal of the Society of Naval Architects of Japan 1958,102：1-5.

[7]Hosoda R.Side wall effects of towing tank on the results of experiments in waves(1)[J].Journal of the Society of Naval Architects of Japan,1976,139：23-30.

[8]Hosoda R.Effect of side-wall interference of towing tank on the results of experiments in waves(2)[J].Journal of the Society of Naval Architects of Japan,1978,143：52-60.

[9]Takaki M.Effects of breadth and depth of restricted waters on longitudinal motions in waves[J].Journal of the Society of Naval Architects of Japan,1979,146：173-184.

[10]Kashiwagi M.3-D integral-equation method for calculating the effects of tank-wall interference on hydrodynamic forces acting on a ship[J].Journal of the Japan Society of Naval Architects and Ocean Engineers,1989,212：89-101.

[11]Kashiwagi M,Ohkusu M.Side-wall effects on hydrodynamic forces acting on a ship with forward and oscillatory motions [C].Proceedings of 5th International Conference on Numerical Ship Hydrodynamics,1989：499-511.

[12]Iwashita H,Hidaka Y,Kishimoto K.Side wall effects of a towing tank on the measurement of unsteady waves of ships advancing in waves[J].Journal of the Japan Society of Naval Architects and Ocean Engineers,2011,102：21-33.

[13]Xu Y,Dong W-C.Study on characteristics of 3-D translating-pulsating source Green function of deep-water Havelock form and its fast integration method[J].China Ocean Engineering,2011,25(3)：365-380.

[14]Zong Z,Huang D-L.Numerical studies on potential of a 3-D pulsating source in uniform stream[J].Journal of Hydrodynamics,1991,6,55-63.

[15]Du S-X,Wu Y-S.A fast evaluation method for Bessho form translating-pulsating source Green’s function[J].Shipbuilding of China,1998,141(2)：40-48.

[16]Hong L,Zhu R C,Miao G P,Fan J.Numerical calculation and analysis of 3-D Green’s function with forward speed in frequency domain[J].Journal of Hydrodynamics,2013,28(4)：423-430.

[17]Liu Y Z,Miao G P.Theories of ship’s motions in waves[M].Shanghai：Publishing House of Shanghai Jiaotong University, 1986.

[18]Dai Y S,Duan W Y.Potential flow theory of ship motion in waves[M].Beijng：National Defense Industry Publishing House,2008.

[19]Noblesse F,Hendrix D.On the theory of potential flow about a ship advancing in waves[J].Journal of Ship Research, 1992,36(1)：17-29.

[20]Xu Y,Dong W C,Xiao W B.Study on far field wave patterns and their characteristics of Havelock form Green function [J].China Ocean Engineering,2013,27(3)：283-298.

[21]Xiao W B,Dong W C.Decomposition of the unsteady wave patterns for Bessho form translating-pulsating source green function[J].Journal of Ocean University of China,2014,13(5)：771-776.

[22]Xu Y,Dong W C.Numerical study on wave loads and motions of two ships advancing in waves by using three-dimensional translating-pulsating source[J].Acta Mechanica Sinica,2013,29(4)：494-502.

[23]Xu Y,Dong W C.Valid hydrodynamic interaction regions of multiple ships advancing in waves[J].Journal of Hydrodynamics,2013,25(6)：856-866.

波浪中航行两船模池壁干扰效应的数值研究

肖汶斌
（国防科技大学海洋科学与工程研究院，长沙410073）

对规则波中顶浪并行航行的两船模，基于频域移动脉动源格林函数建立了有效表达池壁效应的三维数学模型，该模型采用分布源积分方法求解近距航行两船模的波浪作用力和运动响应，并利用镜像原理将水池格林函数表示为开阔水域的格林函数和由镜像点源组成的无穷级数。分析移动脉动源格林函数的远场传播模态及其特性可知，当τ＞0.272（τ为斯特劳哈尔数）时各传播波模态均不在点源的上游出现，故此时点源波系的影响范围可由环形—扇形波的半楔角确定，在此基础上计及船模辐射—绕射波的池壁反射作用对自身和另一船模的干扰，依据船型要素、水池宽度和两船相对位置，采用六个几何临界半楔角表征船体的辐射—绕射波，提出了并行航行两船模的池壁效应判别方法。数值研究表明：不同镜像次数下水池格林函数的数值差异主要体现在距船艏较远处，在兼顾计算精度与效率的原则下可选取有限项级数的水池格林函数作为积分内核，而池壁效应对近距航行两船运动响应的影响主要体现在长波区。

两船；池壁效应；格林函数法；移动脉动源；模型试验

U661.32

：A

国家重点研发计划项目（No.2016YFC1401800），国防科技大学科研计划项目（ZK16-03-46）

肖汶斌（1988－），男，博士，国防科技大学海洋科学与工程研究院助理研究员。

1007-7294（2017）03-0295-14

U661.32

：A

10.3969/j.issn.1007-7294.2017.03.005

Received date：2016-08-16

Foundation item：Supported by the National Key Research and Development Project of China(No.2016YFC1401800) and the Scientific Research Project of NUDT(NO.ZK16-03-46)

Biography：XIAO Wen-bin(1988-),male,Ph.D.,research assistant,E-mail：hgxiaowb727@126.com.