Coupled Hydrodynamic and Aerodynamic Response Analysis of a Tension-Leg Platform Floating Wind Turbine

SHEN M-cheng,HU Zhi-qing,b,GENG Tin

(a.School of Naval Architecture,Ocean and Civil Engineering;b.State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University,Shanghai 200240,China)

Coupled Hydrodynamic and Aerodynamic Response Analysis of a Tension-Leg Platform Floating Wind Turbine

SHEN Ma-chenga,HU Zhi-qianga,b,GENG Tiana

(a.School of Naval Architecture,Ocean and Civil Engineering;b.State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University,Shanghai 200240,China)

A fully coupled time-domain aero-hydro-servo-elastic simulation of a tension-leg-platform (TLP)floating wind turbine is conducted.3-D potential theory and Morison equation are applied to calculate the hydrodynamic loads.Blade element momentum theory and generalized dynamic wake theory are applied to calculate the aerodynamic loads.Time series results are obtained and analyzed to study the coupled dynamic responses of the TLP floating wind turbine.An analytic equation governing the surge motion was formulated and solved based on perturbation method.This equation can explain the high frequency response in surge motion induced by the nonlinearity of viscosity.From the analysis results,the dynamic responses of the TLP floating wind turbine are obtained and analyzed, and it is found that the high frequency component of the response has significant impact on the platform’s dynamic performance.

floating wind turbine;TLP;dynamic response;coupled aerodynamic and hydrodynamic loads;nonlinear drag force

0 Introduction

The offshore wind power is a promising renewable energy resource.Tension-Leg-Platform (TLP)can play an important role and provide a desirable foundation for floating wind turbine because of its steady motion,and thus high energy transformation ratio.But TLP platform is susceptible to high frequency excitation due to its high stiffness mooring system.Typically,the natural frequencies of a TLP platform are designed to avoid the wave frequency effect.But high frequency excitations can be induced by aerodynamic loads,coupled structural responses and nonlinear hydrodynamic loads such as second order forces and viscous effects.It is necessary to include these effects in a time domain simulation to get a realistic estimation of the dynamic response of TLP platform floating wind turbine.

Various studies have been conducted on floating wind turbines.Nielsen[5]analyzed negative aerodynamic damping on a Spar floating wind turbine by using a combined aero-servo-elastic hydrodynamic and mooring program.Wayman and Jonkman[6]conducted a frequency domain analysis on various TLP designs,but transient and nonlinear effects were not considered.Roald[7]investigated the effect of the second order forces on a TLP floating wind turbine which showed importance of high frequency excitation.But the second order forces were calculated in frequency domain,and the tower flexibility was not taken into consideration.Matha[8]studied the response,ultimate loads and fatigue loads of a TLP floating wind turbine by conducting time domain simulation of various load cases,which captured major nonlinear effects. Goupee and Kimball[11]performed model tests for floating wind turbines,from which valuable data were acquired.However,phenomena concerning viscosity could not be simulated accurately in the model test due to scale effect.

This paper studies the coupled dynamic response of a TLP floating wind turbine.Major focuses are put on the effects of steady wind and drag force on the surge and pitch responses. In addition,the derivation and property of drag force induced nonlinear responses,especially high frequency nonlinear responses,are discussed in detail,which have not been seldom analyzed in former researches.

1 Theory and method

The NREL 5 MW Wind Turbine[3]supported by a TLP developed by the University of Maine for use in the DeepCwind project shown in Fig.1 is adopted as the research object.

Tab.1 Principal dimensions and mass properties of NREL 5MW wind turbine

Tab.2 Principal dimensions and mass properties*of TLP

Fig.1 TLP floating wind turbine

The principal dimensions of the wind turbine are listed in Tab.1.The principal dimensions and mass properties of the TLP with wind turbine and moorings are listed in Tab.2[10].

It should be noted that the mass of the TLP is of the same magnitude with those of the wind turbine and the tendons,and thus strong coupled dynamic interactions can be expected among them.Therefore,time domain analysis is necessary to simulate the effects of aerodynamic loads,structural elastic modes,control system and nonlinear wave loads simultaneously. The numerical simulation studied in this paper is conducted using a numerical aero-hydroservo-elastic simulator FAST.

The aerodynamic loads are calculated based on blade element momentum theory coupled with generalized dynamic wake theory.It takes into consideration the time lag in the induced velocities created by vorticity being shed from the blades and being convected downstream. Details about the aerodynamic theories applied by FAST can be found in Ref.[1].

The hydrodynamic loads are obtained from potential theory and semi-empirical Morison equation.Wave forces caused by incident waves and body motions can be calculated in time domain by three-dimensional potential theory.The wave-induced forces include the Froude-Kriloff force due to incident waves,diffraction force due to scattering of incident waves and radiation force due to body motions.

By assuming the floating body as a rigid body,the governing equation for transient motion[11]is written as

where the six degrees of freedom are coupled by added mass and damping derived from radiation forces and restoring forces from the mooring system.

Since potential theory neglects viscosity effects,Morison equation is also applied as a complement to consider quadratic drag force caused by separation of boundary layer in extreme sea states[9].The drag force on unit length of a cylinder is found by equation(2)where ρ denotes the density of the fluid,D denotes the diameter of the cylinder and urdenotes the relative velocity between the fluid particle and the strip of the cylinder.

A control system ensuring constant power generation above rated wind speed is also simulated.The responses of tower and blades are calculated based on superposition method of vibration mode.

2 Load cases definition

Two groups of load cases,the RAO load cases and the design load cases are conducted.The RAO load cases is performed with unit-amplitude regular waves to study the frequency domain response characteristics of the floating wind turbine,while the design load cases with waves and steady wind are performed to verify the survivability in severe sea states.For all load cases,the wind and wave are in collinear direction and the wind turbine is in the upwind condition.The load cases investigated in this paper are listed in Tab.3 and Tab.4,respectively.

Tab.3 RAO load cases

Tab.4 Design load cases

Wind speed is usually related with the severity of sea condition,and strong wind normally induces large wave.Therefore,different wind speeds are chosen depending on the corresponding wave heights and frequencies.Corresponding load cases are carried out without steady wind to study the aerodynamic effect through comparison.

The natural frequencies of the platform[7]are listed in Tab.5.

Tab.5 Natural frequencies of the TLP with rigid and flexible wind turbine blades and tower

A significant discrepancy of pitch and roll natural frequencies between a rigid tower model and a flexible tower model are observed,due to coupling between tower elasticity and platform pitch.

3 Simulation results and discussions

3.1 Unit-amplitude regular wave

Usually,a frequency domain analysis is used for dynamic response analysis of offshore floating structures under the excitation of regular wave.Assuming the whole system is linear, the response can be characterized by RAOs,which equal the response amplitudes normalized by the wave amplitude.However,when nonlinearity is taken into consideration for floating wind turbine,a new concept of the normalized amplitudes,named effective RAOs,was proposed by Jonkman[2],to consider the complicated coupling effect between wave and wind.The effective RAOs for floating wind turbine not only depend on wave frequency but also vary with wave amplitude and the effect of wind load.The word‘effective’is used to clarify that they are not true RAOs when the underlying models are nonlinear[2].

The effective RAOs are obtained by running simulation with periodic,unit amplitude waves with the rotor parked.The effective RAOs are thus obtained at several discretized frequencies and cubic spline fitting is applied to get a smooth curve.Surge and pitch effective RAOs are shown in Fig.2 and Fig.3,respectively.

Fig.2 Surge effective RAO for regular wave only case

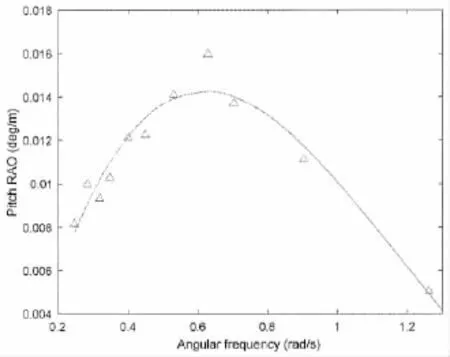
Fig.3 Pitch effective RAO for regular wave only case

It can be observed that surge RAOs are in good accordance with the fitting curve,but pitch RAOs are difficult to be represented by a smooth curve,and at certain frequencies the results at simulated frequencies deviate quite a little from the fitting curve.Such frequencies are 0.628 rad/s,0.448 rad/s and 0.285 rad/s,all of which are close to submultiples of the pitch natural frequency 2.021 rad/s.This deviation phenomenon can be explained from the nonlinearity of viscosity at certain frequencies.It is because that the quadratic drag force induces responses in surge motion whose frequencies are odd multiples of wave frequency.The surge motion induced inertial force contributes a high-frequency moment to the pitch motion and causes resonance when the frequency is close enough to the pitch natural frequency.This is the reason why the effective RAOs in pitch motion seem irregular in certain frequencies.Although the high frequency components in surge motion are small,the inertial-force-induced momentcan be large because the center of mass of the wind turbine is high.This results in stronglycoupled dynamic responses in surge and pitch motion,which is not so conspicuous in traditional TLP platform for oil production.

3.2 Regular wave and steady wind

Aerodynamic effect on the TLP platform wind turbine is investigated by simulating regular wave and steady wind load cases.The effective RAOs of surge and pitch motion with and without wind are plotted in Fig.4 and Fig.5,respectively.

Fig.4 Surge effective RAO for regular wave with and without wind cases

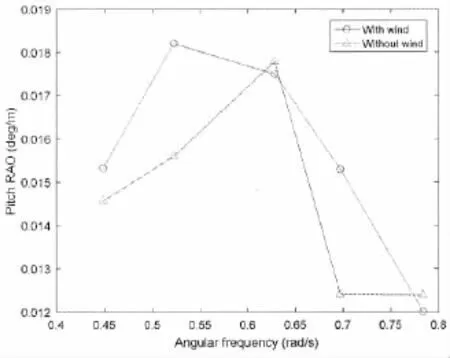
Fig.5 Pitch effective RAO for regular wave with and without wind cases

The surge effective RAOs show great differences compared with the ones presented in section 3.1 at the range of low frequency.This is because the wave heights are large enough to make viscous drag significant.When the wave height increases,the KC number increases as well.The boundary layer is likely to separate at tendons and the surface-piercing pontoon, causing the viscous drag force due to high pressure at the up-stream side and low pressure at the down-stream side.The drag force considered by Morison equation increases quadratically with the wave height,so the drag force plays a dominant role in severe sea states.The reduction in surge effective RAOs at low frequencies is due to the viscous damping effect by the drag force.

The constant wind also contributes damping effect to surge motion,especially when the wind speed is around the rated speed 11.4 m/s.On the contrary,pitch motion is damped by the wind at some frequencies but excited at other frequencies.Since pitch motion is much smaller compared with surge motion,the aerodynamic thrust on the rotor is mainly dependent on the surge velocity.Under the excitation of regular wave,surge velocity and thrust both vary harmonically but in opposite phase.If pitch velocity varies in opposite phase with surge velocity, thus in the same phase with thrust,then aerodynamic thrust will excite pitch motion.Therefore, whether pitch motion is excited or damped by wind force depends on frequency domain response of the platform.Noted that turbulent wind has not yet been taken into consideration,the actual pitch response can be even more strongly excited.

3.3 Irregular wave and steady wind

The JONSWAP spectrum is chosen to simulate irregular waves.Standard deviations of surge and pitch motion are obtained from numerical simulation of each load case equivalent to one and a half hour’s real sea states.The results are plotted in Fig.6 and Fig.7.

Fig.6 Surge response standard deviation

Fig.7 Pitch response standard deviation

The steady wind effect on surge standard deviation is similar to that on surge effective RAOs in regular wave cases.This is understandable because standard deviation and RAOs are both measurement of deviation from mean values.However,it is not the case in pitch motion, because the wind force also contributes irregular disturbance to rotor thrust.Pitch motion is more susceptible to variation in rotor thrust than surge motion is,since the center of rotor is high above the tower base,resulting in great variation of pitch moment.This may cover up the damping effect in pitch motion around rated wind speed.In contrast,the damping effect in surge motion predominates the disturbance in surge motion.Therefore,surge and pitch respond differently to the aerodynamic loads.

Pitch spectrum density functions under the excitation of irregular wave with and without wind are plotted in Fig.8.The wave peak frequency is 0.448 8 rad/s.The significant wave height is 10 m,and the wind speed is 40 m/s. Viscosity effect is of crucial importance in this case.In the wave-only case,the viscosity induced high frequency pitch motion is comparable with the wave frequency motion as the solid line shows.The dotted line shows that the aerodynamic load increases the wave frequency motion while reduce the natural frequency resonance considerably.This is because aerodynamic damping is the majority of total damp-ing at high frequency.Total damping around resonance frequency has a very important effect on the amplitude of resonance motion.According to potential theory,wave radiation damping tends to vanish at high frequency while aerodynamic damping is approximately proportional to cubic of frequency[4].Therefore,the existence of aerodynamic damping significantly reduces the resonance in pitch motion.

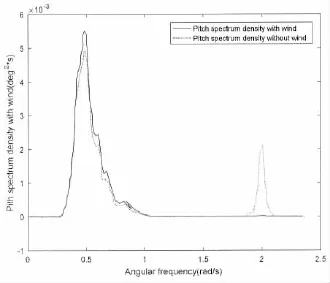
Fig.8 Pitch response spectrum density

3.4 Viscosity effect

Two major effects of the viscosity induced drag force have been discovered in the time domain simulation,and they are non-zero average displacement caused by mean drift forces and high frequency responses caused by the coupled effect of wave frequency responses and drag force.

An approximate differential equation governing surge motion is formulated as Eq.(3)to investigate qualitative property of the nonlinear effect.Asymptotic behaviors of amplitudes of the mean displacement and high frequency responses can be found by solving this equation.

where M denotes the sum of mass of the platform and wind turbine and added mass due to fluid motion,x denotes the surge displacement,C denotes the coefficient of drag force for surge motion,U denotes the amplitude of fluid horizontal velocity at mean position of the platform,ω denotes the wave angular frequency,T denotes the pre-tension of the tension leg,L denotes the length of the tension leg and F denotes amplitude of the excitation force in surge motion.α denotes the phase difference between the fluid velocity and the excitation force.

Several approximations and assumptions are made to build up this equation.These approximations and assumptions include but not exclusively：

(1)The platform responses approximately harmonically at the wave frequency.Therefore, time domain equation containing convolution term degenerates into frequency domain equation.

(2)Wave radiation damping is negligible compared to drag force and thus being neglected.

(3)The surge motion is small compared with the wave length and the characteristic length of the platform.Therefore,the velocity of fluid particle at instantaneous position is replaced by that at mean position and the restoring force from tension legs is linearized at mean position.

(4)Airy wave theory is applied and the amplitudes of fluid velocity and excitation force are all proportional to wave height.

Following quantities are introduced to simplify Eq.(3)：h denotes wave height,u denotes transfer function of fluid horizontal velocity at mean position of the platform and f denotes transfer function of surge excitation force.

The natural frequency of the undamped mode is given by

For normal sea states,the corresponding quantity ε is a small parameter.Therefore,Eq. (4)can be solved using perturbation method by expanding X into an asymptotic series as follows[12].

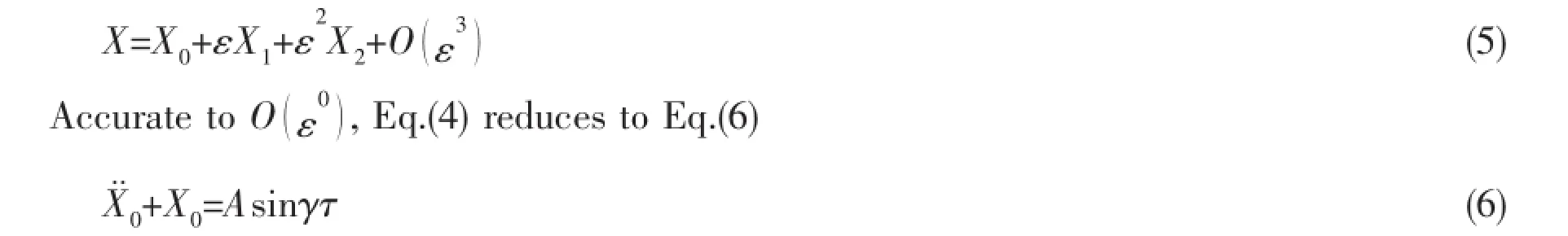
In fact,Eq.(6)corresponds to the linearized equation for frequency domain analysis.The steady state solution to Eq.(6)is

This solution corresponds to the wave frequency response.

In Eq.(7),A0and φ0are simple functions of A and γ,which need not be shown explicitly.This convention is also applied in following deduction to avoid lengthy expressions.

By substituting Eq.(7)into Eq.(8),Eq.(9)is obtained.

The right hand side of Eq.(9)is a periodic function,so it can be expanded into a Fourier series as follows：

This excitation term for X1is the derivation of high frequency excitation.

The solution to Eq.(9)is

It can be easily shown that the asymptotic behavior of coefficient anis an∝1/n3if n is odd and an=0 if n is even.Therefore,the amplitude of high frequency response decays inverse-proportionally to cubic of the frequency.Small as it is,it can be detrimental if it coincides with pitch natural frequency.

By applying former results,Eq.(12)is simplified to give

Third power function is applied to fit the data points.The result is in good accordance with the prediction derived from the perturbation analysis,and thus verifies the model.

Time series of pitch motion under the excitation of regular wave with 0.285 6 rad/s peak frequency and 2 m wave height is shown in Fig.10.Transient motion due to initial condition quickly vanishes because of strong damping effect of viscosity,and the pitch motion shown in Fig.10 is in steady state.It is obvious that there is a high frequency component superposing upon the wave frequency component and the time average of pitch motion is nonzero.Fast Fourier Transformation of the time series result is shown in Fig.11.There are four major components.The highest peak is the wave frequency motion.The second highest peak corresponds to mean drift displacement.The small peak around 0.85 rad/s corresponds to three times the wave frequency and is induced by drag force.But it does not coincide with pitch natural frequency,so the amplitude of this motion is negligible.The corresponding frequency to the thirdhighest peak,i.e.about 2 rad/s happens to be seven times the wave frequency.It is also induced by drag force and causes considerable resonance in pitch motion.This phenomenon should be taken into consideration in future design of TLP platform wind turbine and should be avoided if possible.

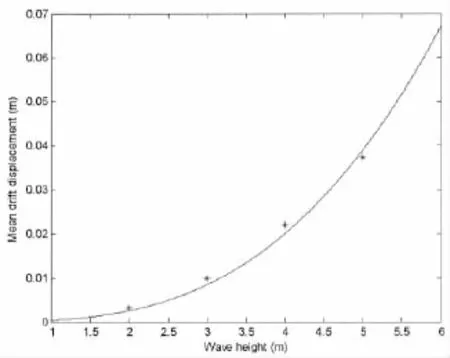
Fig.9 Surge mean drift displacement

Fig.10 Time series of pitch motion

Fig.11 Fast Fourier Transformation of pitch motion

4 Conclusions

Responses in surge and pitch motion of the TLP platform floating wind turbine to aerodynamic and hydrodynamic loads have been investigated.

Aerodynamic loads generally have damping effect on surge motion,which reduce surge response.The damping effect is most significant around rated wind speed.Aerodynamic loads have both damping and exciting effect on pitch motion.It depends on the relative phase between pitch motion and thrust force.In irregular wave cases,exciting effect covers up damping effect while damping effect plays an important role when resonance occurs in pitch motion.

Hydrodynamic loads dominate platform motion.When wave height is small,linear hydrodynamic forces dominate.When wave height is large,nonlinear drag force induced by viscosity dominates.The drag force contributes damping but also causes mean drift and high frequency responses.The resulted high frequency response in pitch motion is detrimental to TLP if it coincides with pitch natural frequency,which may cause fatigue and even serious failure of the tendons.Qualitative property of the mean drift and high frequency responses are exploited by perturbation analysis and in good accordance with the numerical results.

[1]Moriarty P J,Hansen A C.AeroDyn theory manual[M].Colorado：National Renewable Energy Laboratory,2005.

[2]Jonkman J.Memorandum-Load Case 5.4 from OC3 Phase IV(Floating)[M].Colorado：National Renewable Energy Laboratory,2009.

[3]Jonkman J.Dynamics modeling and loads analysis of an offshore floating wind turbine[M].Colorado：National Renewable Energy Laboratory,2009：94-95.

[4]Karimirad M.Stochastic dynamic response analysis of spar-type wind turbines with catenary or taut mooring systems[D]. Norwegian：Norwegian University of Science and Technology,2011.

[5]Nielsen F G,Hanson T D,Skaare B.Integrated dynamic analysis of floating offshore wind turbines[C]//European Wind Energy Conference,May,2007.Milan,Italy,2007：7-10.

[6]Wayman E N,Sclavounos P D,Butterfield S,et al.Coupled dynamic modeling of floating wind turbine systems[C]//Offshore Technology Conference,May,2006.Houston,Texas,2006：1-10.

[7]Roalda L,Jonkman J,Robertson A,et al.The effect of second-order hydrodynamics on floating offshore wind turbines [C]//Deep Sea Offshore Wind R&D Conference,January,2013.Trondheim,Norway,2013：260-263.

[8]Matha D.Model development and loads analysis of an offshore wind turbine on a tension leg platform,with a comparison to other floating turbine concepts[D].Colorado：University of Colorado-Boulder,2009.

[9]Faltinsen O M.Sea loads on ships and offshore structures[M].Cambridge：Cambridge University Press,1999.

[10]Goupee A J,Koo B,Lambrakos K F,et al.Offshore wind energy：Model tests for three floating wind turbine concepts[C]// Offshore Technology Conference,May,2012.Houston,Texas,2012：455-465.

[11]Mei C C,Stiassnie M,Yue K P.Theory and applications of ocean surface waves[M].Cambridge：World Scientific,2005.

[12]Mei C C.Mathematical analysis in engineering[M].Cambridge：Cambridge University Press,1997.

张力腿式浮式风机平台的水动力和空气动力耦合响应分析

沈马成a，胡志强a，b，耿添a
（上海交通大学a.船舶海洋与建筑工程学院；b.海洋工程国家重点实验室，上海200240）

文章采用了空气动力、水动力、控制与弹性完全耦合的时域模拟方法研究了张力腿式浮式风机平台的动力响应。水动力载荷的计算采用了三维势流理论与Morison公式。空气动力载荷的计算采用了叶素动量理论和广义动态尾流理论。利用FAST软件得到了张力腿式浮式风机平台响应的时域结果，并分析了其动力响应特性。建立了描述平台纵荡运动的非线性微分方程，并采用了摄动方法求得其近似解，解释了纵荡运动中由非线性粘性效应引起的高频响应。对数值模拟结果的分析表明高频的响应分量对平台的动力性能有显著的影响。

浮式风机平台；张力腿平台；动力响应；耦合的空气动力与水动力载荷；非线性拖曳力

U661.43

：A

沈马成（1993－），男，上海交通大学船舶海洋与建筑工程学院本科生；

1007-7294（2017）03-0263-12

U661.43

：A

10.3969/j.issn.1007-7294.2017.03.002

胡志强（1975-），男，上海交通大学船舶海洋与建筑工程学院副教授，通讯作者；

耿添（1993-），男，上海交通大学船舶海洋与建筑工程学院本科生。

Received date：2016-11-02

Foundation item：Supported by the Natural Science Foundation of China(Grant No.51239007)

Biography：SHEN Ma-cheng(1993-),male,B.S.E.,graduate student,E-mail：macshen@umich.edu;

HU Zhi-qiang(1975-),male,associate professor,corresponding author,E-mail：zhqhu@sjtu.edu.cn.