合理设置疑问，提升学生数学探究能力

江苏省扬州市邗江区瓜洲中学(225129)

朱 宏●



合理设置疑问，提升学生数学探究能力

江苏省扬州市邗江区瓜洲中学(225129)

朱 宏●

数学是思维的体操.数学课堂离不开问题，数学课堂上，唯有教师科学合理地设置疑问，方能引领学生的思维向纵深发展，真正培养和发展学生的自主探究能力.高中数学课堂，更是思维火花不断迸发和闪耀的所在，作为课堂活动的引导者，教师要巧妙设计，把握最佳时机，切入问题，激起学生思维的涟漪，让高中数学课堂始终沉浸在高效的氛围中.

高中数学;疑问;探究

一、在教学开端处设置疑问，打开学生思维入口

以设置疑问的方式开始课堂教学是一个十分高效的方法.当学生们感兴趣的疑问出现之后，大家便会很自然地对之加以关注，并主动寻找解决这个疑问的办法.在这个过程中，主体教学的展开也会顺利许多.

例如，在对抛物线的内容开始教学之前，我先向学生们提出了这样一个问题：在一条小河上架设有一座小桥，小桥的形状可以近似看作一条抛物线.经测量后发现，当河面距离小桥的拱顶部分5米的时候，河面的宽度是8米.现有一条宽度为4米的小船行驶在河面上，船的高度是2米，当小船上装满货物之后，小船露出河面之上的部分高度是0.75米.那么，随着水面高度的不断上涨，当其距离小桥拱顶多高时，这条小船就无法顺利通过了？根据题目条件的叙述，学生们建立起平面直角坐标系，画出了抛物线的图形，将小船、河面及拱桥的状态示意出来.但大家发现，想要将其中的数量关系计算出来，必须要对抛物线的方程及相关性质有所知晓才可以进行.于是，学生们产生了对深入研究抛物线知识的积极愿望，并对自己可能将会接触到的内容有了一定的心理预期.

在教学开端处设置疑问，让学生们的思维从一开始就打开了.大家不仅燃起了求知的热情，更从感性上对将要学习的知识内容有了一个轮廓上的认知.这为学习活动的正式开展提供了一个很好的前提基础，是高效教学的原动力.

二、在教学开展中设置疑问，引导学生思维深化

疑问设置在课堂教学的主体部分也是适用得十分广泛的.在这个阶段，疑问就像是一只无形的手，引领着学生们的思维在教师预设的轨道上发展.因此，如果能够将教学目标或思路巧妙融入到为学生们所设计的疑问之中，将会显著提升课堂教学的效率.

例如，在对函数的内容展开教学时，为了让学生们的知识思维不断深化，我为大家设置了这样一连串问题：已知，a是一个实数，并有函数f(x)=2x2+(x-a)|x-a|，(1)如果f(0)≥1，那么实数a的取值范围是什么？(2)能否求出函数f(x)的最小值？(3)如果有一个函数h(x)=f(x)，x∈(a,+∞)，那么，函数h(x) ≥1的解集是什么？上述几个疑问的设置，是按照分析难度与思维深度不断递增的顺序排列的，随着对这几个问题的思考，学生们对于函数知识的理解逐步走向了灵活与深入.通过对这几个问题的设置特点加以总结，学生们也发现了研究函数问题的普遍思维顺序：对于一个函数，先找特殊情况，再由特殊推向一般，最后从此函数延伸到与之相关联的彼函数，对新的函数加以认知.不仅是针对这道题目本身，这样的问题设置对学生们的数学学习思路都起到了很好的启示性作用.

在教学开展过程中设置疑问的方式有很多，笔者应用频率比较高的是以层层递进的形式呈现疑问.这样的处理能够让学生们的思维随着疑问的逐步深入而得以深化.无需教师添加过多言语上的引导，也可以实现很理想的教学效果.

三、在教学结尾处设置疑问，升华学生思维层级

不要认为，课堂教学告一段落了，便不再需要设置疑问了.数学知识的探究是没有穷尽的，对于它的疑问与思考自然也是不会停止的.作为进一步升华学生思维层级的有效途径，设置疑问不得不提.

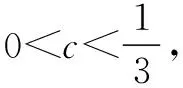
将具有开放性与探究性的疑问在教学结尾处提出，将学生们的思维置于一个未完待续的状态.学生们意识到，原来现有的知识还可以有这么多继续发散的可能.随着对这些疑问的深入思索，学生们也就很自然地完成了一次更加深入的探究.长此以往，学生们的思维能力会得到升华，对于整个高中数学学习来讲都是大有助益的.

按照教学开展的时间顺序来设置疑问是很好的处理方式.在每一个教学阶段，学生们的知识状态都是不同的，自然需要不同的教学处理.教师们顺应这个状态特点，设置不同侧重的疑问，也是颇合时宜的.通过疑问的合理设置，推动了教学活动的有机运转，并在必要之处强化了学生们的思维能力，完善了高中数学教学的高效面貌.

[1]吴晓平.设置“探究”活动,培养“探究”能力[J].《福建中学数学, 2013(4):35-37

[2]杜鹃.数学教学中提升学生自主探究能力研究[J].成才之路, 2016(36)

[3]孙荣娟.浅谈数学课堂教学中培养学生的探究能力[J].中学课程辅导:教师通讯, 2013(3)

G632

B

1008-0333(2017)12-0030-01