统计分析方法在青少年心理状况研究中的应用
刘丹丹,朱家明,黄婷婷
(安徽财经大学 统计与应用数学学院,安徽 蚌埠 233030)
统计分析方法在青少年心理状况研究中的应用
刘丹丹,朱家明,黄婷婷
(安徽财经大学 统计与应用数学学院,安徽 蚌埠 233030)
针对青少年心理状况问题,使用方差分析、变异系数等统计方法,辅助SPSS、MATLAB软件,得出不同年龄段青少年的心理状况存在差异,年龄是驱使青少年施加暴力等行为的主要诱因.通过分析正负框架下各领域的自变量权重,得出正向框架下的主要影响因素为风险偏好,其次为认知需要;负向框架下的主要影响因素为风险偏好,其次为决策风格.最后基于研究结果对我国教育事业的发展提出了一些建议.
青少年心理状况;风险偏好;方差分析;变异系数;正负框架
近年来校园霸凌事件频繁发生,“霸凌”一词迅速发酵成为热点,引起广大人民群众的关注.发生在校园中的暴力事件对青少年心理健康的危害程度是极大的,如果没有受到专业的心理引导,受害者有可能转变为报复社会的人,进而从受害者转变为施暴者,将自己的遭遇原封不动或放大百倍地转嫁到他人身上[1].因此对于这些情况我们应该给予高度的重视,及时了解成因并进行积极干预,预防和避免此类状况的再发生.本文通过对不同年龄段青少年心理状况的问卷调查结果进行分析,试图研究青少年存在潜在心理问题的主要原因,为我国的教育事业发展提出一些有效的建议.
1 数据获取与预处理
1.1 数据获取
本文数据来源于2016年第九届“认证杯”数学建模网络挑战赛,该比赛设计了一次针对不同年龄段青少年心理状况的问卷调查,涉及生命教育、生活方式、娱乐三个领域,包括正向和负向两个框架.自变量包括风险偏好、认知需要、决策风格三个主要方面,其中决策风格又分为理智型、直觉型、依赖型、回避型、冲动型五个维度,每个方面的题目可以按照选择的答案来计算相应的得分.本文旨在利用调查的结果进行分析,判断各个年龄段的心理状况是否存在显著性差异以及分析不同框架下的主要影响因素.
1.2 数据预处理
⑴数据的重新组合
通过对调查所得数据的观察,我们发现在原有数据分组中年龄分布存在一定的交叉,9岁组包含8到13岁6个年龄;11岁组包含10到14岁5个年龄;13岁组包含12到17岁6个年龄;15岁组包含14到18岁5个年龄;17岁组中包含16到20岁5个年龄.因此我们对8到20岁这13个年龄进行重新分组:9岁组(8-10岁)、11岁组(11-12岁)、13岁组(13-14岁)、15岁组(15-16岁)、17岁组(17-20岁).
⑵异常数据处理
通过对数据进行分析发现,在8岁和20岁两个年龄上分别只有一组数据,样本量过少不具有代表性,因此可以剔除.剔除后的分组为:9岁组(9-10岁)、11岁组(11-12岁)、13岁组(13-14岁)、15岁组(15-16岁)、17岁组(17-19岁).
2 基于变异系数法的不同年龄段各指标的权重确定
2.1 研究思路
为了使不同年龄段的青少年心理状况得分具有可比性,有必要计算出各年龄段风险偏好、认知需要、决策风格这三个自变量的权重.本文采用变异系数法来确定不同年龄段各指标的权重.
2.2 数据处理与分析
⑴决策风格得分量化
对于决策风格这一变量,文中只给出理智型、直觉型、依赖型、回避型、冲动型这五个维度的得分,为了便于分析,我们通过赋分值将其量化,所赋分值如表1所示:

表1 五种决策风格的分值转换情况
通过赋分情况不难发现,青少年的决策风格得分越高,其心理状况越好.
⑵自变量的标准化处理
通过对数据进行分析,我们发现风险偏好、认知需要、决策风格这三个自变量的量纲存在较大差异,因此有必要进行标准化处理.
本文采用min-max标准化处理方法:
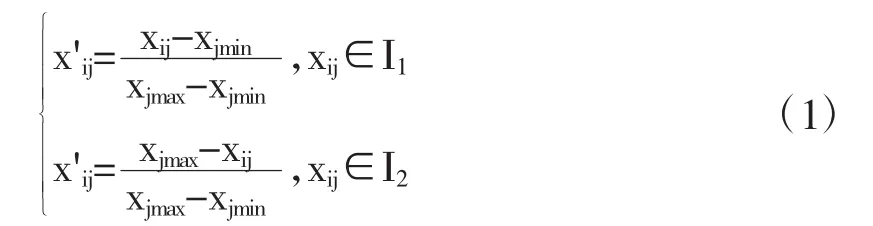
式(1)中,xij为该年龄组第i个学生第j项指标的值,xjmax为第j项指标的最大值,xjmin为第j项指标的最小值,x'ij为该年龄组第i个学生第j项指标标准化后的值.I1表示效益型指标,I2表示成本型指标.
⑶变异系数法确定权重
计算各指标的变异系数公式为:


利用MATLAB编程计算,得到不同年龄段各指标的权重结果如表2所示:
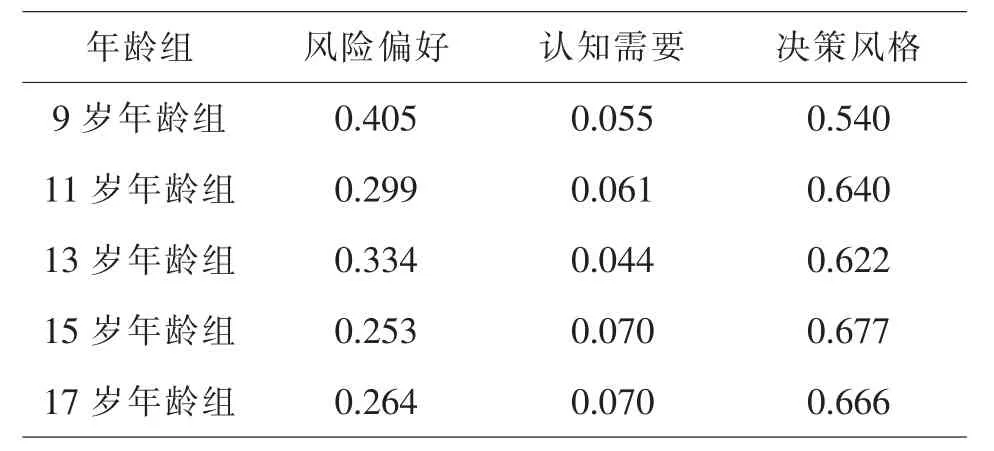
表2 不同年龄段各指标的权重
得到各指标的权重后,可将标准化后的指标与权重加权求和,得到不同年龄段青少年的心理状况得分.
3 基于方差分析的各个年龄段心理状况显著性差异判别
3.1 研究思路
本文假设所给样本量已足够大,数据近似服从正态分布,因此可以通过方差分析判断各个年龄段的心理状况是否有显著的差异.
3.2 研究方法
方差分析是从观测变量的方差入手,研究诸多控制变量中哪些变量是对观测变量有显著影响的变量,对观测变量有显著影响的各个控制变量不同水平以及其交互搭配是如何影响观测变量的[3].
方差分析的基本步骤如下:
⑴建立假设检验,即提出原假设和备择假设
H0:a1=a2=Λ=ak=0,即不同水平下的控制变量对观测变量均值没有显著性影响,
H1:ai不全为0.
⑵计算检验统计量G

式(4)中,SSA为组内离差平方和,SSE为组间离差平方和,k-1、n-k分别为SSA与SSE的自由度.F统计量消除了水平数和样本量对分析带来的影响.若F显著大于1,则拒绝原假设;若F接近1,则接受原假设.
⑶确定P值,选择显著性水平α,对假设检验做出决策
若P值小于α,则拒绝原假设,认为ai不全为0,控制变量不同水平下观测变量各总体均值存在显著差异,控制变量不同水平对观测变量均值产生了显著影响;若P值大于α,则接受原假设,认为a1=a2=Λ=ak=0,控制变量不同水平对观测变量均值没有产生显著影响,观测变量值的变化是由抽样误差引起的[4].
3.3 软件实现及结果分析
将得到的不同年龄段青少年的心理状况得分导入SPSS软件中进行单因素方差分析,得到表3:
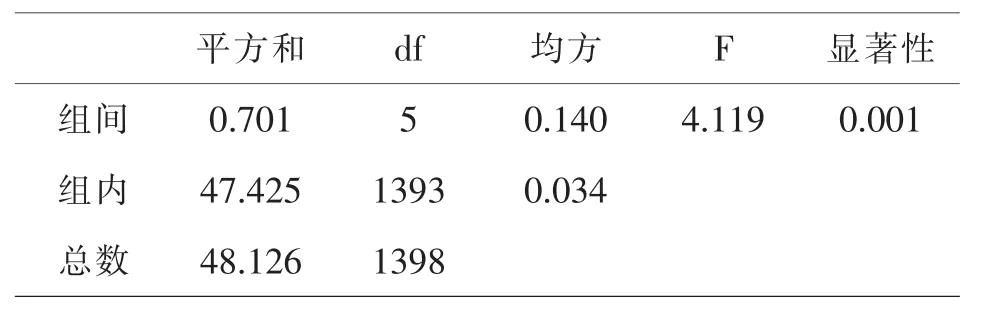
表3 ANOVA单因素方差分析
由表3的结果可知,F统计量的值为4.119>1,对应的显著性水平为0.001<0.05,所以在0.05的显著性水平下可以认为五个年龄段青少年的心理状况存在显著性差异.
4 基于变异系数法分析不同框架下的主要影响因素
4.1 研究思路
通过对问题进行分析可知,原数据分为生命教育、生活方式、娱乐三个领域,对于各个领域分为正向、负向两种框架,这两种框架有二选一式的评价变量,用A或B来表示,并且由风险偏好、认知需要、决策风格三个主要方面来决定.因此,我们对框架进行多层次的分类,其中,每一层都是对上一层的细化分类.
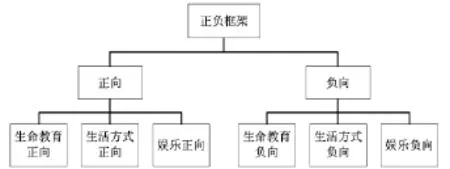
图1 框架图
研究不同框架下的主要影响因素仍可以采用上面介绍的变异系数法.采用变异系数法确定影响正、负向框架各领域的评价变量取值的自变量的权重,综合各领域的评价变量取值的自变量的权重得到正负框架下的自变量的权重.最后按照权重越大,影响越大的原则,进而可以确定不同领域的主要影响因素.
4.2 结果实现及分析
利用MATLAB编程计算,得到影响正、负向框架各领域的评价变量取值的自变量权重如表4所示:
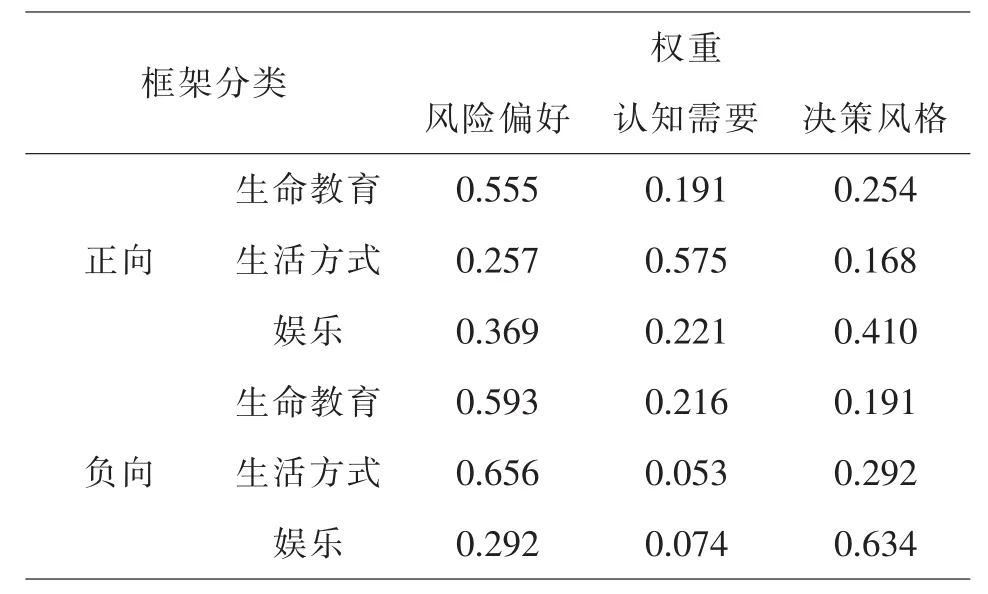
表4 影响正、负向框架各领域的评价变量取值的自变量权重
根据得到的权重可以分析出正负框架下不同领域的主要影响因素,如表5所示:

表5 正负框架下不同领域的主要影响因素
因为在正负框架下生命教育、生活方式、娱乐三个领域没有相对重要性之分,因此可以通过求和后归一化得到影响正、负向框架的自变量的权重如下表6所示:
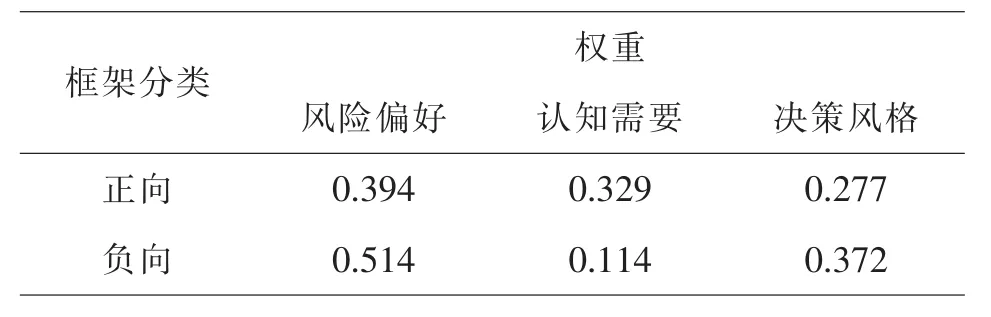
表6 正负框架下的主要影响因素的权重
由表6的结果可知,正向框架下的影响因素主要为风险偏好,其次为认知需要;负向框架下的影响因素主要为风险偏好,其次为决策风格.
5 结束语
本文通过研究发现不同年龄段的心理状况存在显著性差异,故我们应有针对地对处于青春期的学生进行着重的教育,在风险偏好、认知需求、决策风格三个方面给予他们的正确引导,在生活中潜移默化地降低其潜在心理问题的可能性,从而抑制校园霸凌事件的发生.同时,对于教育知识的选取,在正向、负向两种不同框架下应进行不同方面的侧重.对于正向框架下的正确教育知识,应侧重于风险偏好、认知需求方面;对于负向框架下的正确教育知识,应侧重于在风险偏好、决策风格方面.
〔1〕张自然.面对校园暴力,美法两国零容忍[N].中国教师报,2015-09-30(003).
〔2〕杨桂元.数学建模[M].上海:上海财经大学出版社,2015.112-116.
〔3〕高忠江,施树良,李钰.SPSS方差分析在生物统计的应用[J].现代生物医学进展,2008,8(11):2116-2120.
〔4〕梁坤宇,张超,曹明宏.YH公司员工满意度调查:分析与对策[J].中国农业银行武汉培训学院学报,2012(6):78-80.
〔5〕谢银迪.美国:“霸凌零容忍”[J].上海教育,2015 (35):25-29.
〔6〕任亚珍,顿晓明.青少年心理健康状况研究[J].读天下,2016(9):11-13.
〔7〕张良良.关于青少年心理健康状况的研究[J].商, 2016(14):83-83.
〔8〕李娟,殷仕淑,高彦文,李冬梅.基于典型相关的青少年心理健康影响因素研究[J].阜阳师范学院学报(自然科学版),2016(04):93-97.
B844.2
A
1673-260X(2017)04-0044-03
2017-02-14
国家自然科学基金资助项目(11601001);安徽财经大学教研资助项目(acjyzd201429)
朱家明(1973-),男,安徽泗县人,安徽财经大学统计与应用数学学院数学建模实验室主任,副教授,硕士,研究方向:应用数学与数学建模

