对称性在定积分近似计算中的应用

赵丽丽

（赤峰学院 计算机与信息工程学院 内蒙古 赤峰 024000）

对称性在定积分近似计算中的应用

赵丽丽

（赤峰学院 计算机与信息工程学院 内蒙古 赤峰 024000）

在定积分的近似计算中，梯形法、抛物线法往往需要计算的函数值的个数比较多，但对于一些有对称性的函数，在进行定积分近似计算时利用对称性可以减少函数值的计算量.本文将对四种有对称性的函数进行讨论，以供参考.

定积分；近似计算；误差估计；对称性

1 引言

在定积分的近似计算中，被积函数f(x)往往具有某些对称性，本文是在利用复化梯形求积公式、复化抛物线求积公式求定积分的基础上，对三种有对称性的函数（1）对称区间上的偶函数.（2）函数f(x)在区间[0,a]上可积且有f(x)=f(a-x).（3）函数f(x)连续且f(x)的图像关于直线x=a对称进行讨论，得出在近似计算中，利用这些对称性可以保证在误差不超过ε的前提下，减少函数值点的计算个数.

2 若函数f(x)为[-a,a]上的偶函数则有f(x)dx=2f(x)dx(1)

2.1 定理1 设函数f(x)为[-a,a]上的偶函数，用复化梯形求积公式计算并要求误差不超过ε，则需要计算个点的函数值.而利用公式计算可在保持精度不变下减少计算个点的函数值.

对于上述ε，根据公式（1）把区间[0,a]m等分，利用复化梯形求积公式计算根据结论1可得其中，因为M≥M1，取，因此需要算个点的函数值，因为，所以

2.2 定理2 设函数f(x)为[-a,a]上的偶函数，用复化抛物线求积公式计算并要求误差不超过ε，则需要算个点的函数值，而利用公式计算可在保持精度不变下减少计算个点的函数值.

对于上述ε，根据公式（1）把区间[0,a]m等分并令m=2l，利用复化抛物线求积公式计算根据结论2可得，其中因为M≥M1，取N1=，因此需要算个点的函数值.因为，所以

3 设函数f(x)在区间[0,a]上可积且有f(x)=f(a-x)则有

3.1 定理3 设函数f(x)在区间[0,a]上可积且有f(x)=f(a-x)，用复化梯形求积公式计算并要求误差不超过ε，则需要算个点的函数值.而利用公式计算可在保持精度不变下减少计算个点的函数值.

3.2 定理4 设函数f(x)在区间[0,a]上可积且有f(x)=f(a-x)，用复化抛物线求积公式计算并要求误差不超过ε，则需要算个点的函数值，而利用公式计算可在保持精度不变下减少计算个点的函数值.

3.3 引理1 若f(x)在[a-h,a+h]上连续，则有

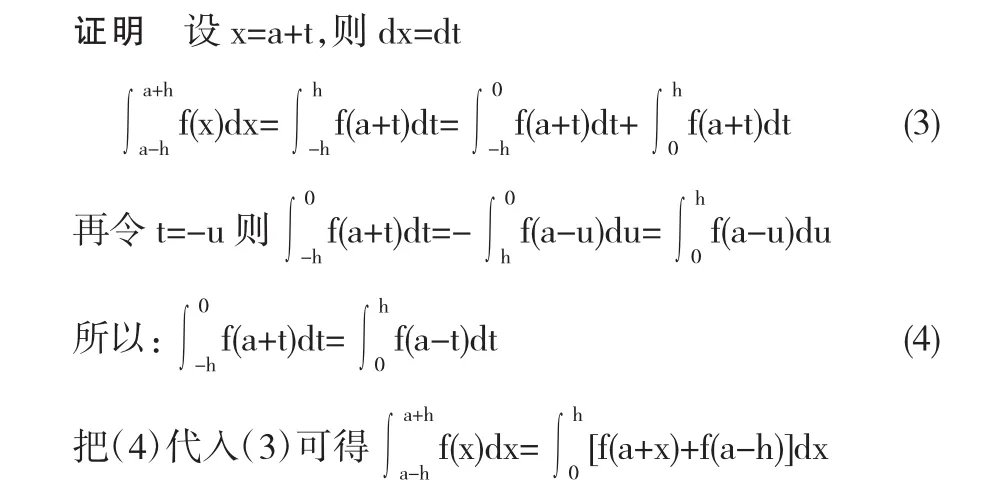
4 若f(x)连续且y=f(x)的图形关于直线x=a对称f(a+x)=f(a-x)，

4.1 定理5 若f(x)连续且y=f(x)的图形关于直线x=a对称，对一切h＞0，用复化梯形求积公式计算并要求误差不超过ε，则需要算个点的函数值，而利用公式，可在保持精度不变下减少计算个点的函数值.

4.2 定理6 若f(x)连续且y=f(x)的图形关于直线x=a对称，对一切h＞0，用复化抛物线求积公式计算并要求误差不超过ε，则需要算个点的函数值，而利用公式可在保持精度不变下减少计算个点的函数值.

〔1〕徐萃薇,孙绳武.计算方法引论(第二版)[M].北京:高等教育出版社,2002.

〔2〕张德荣,王新民,高安民.计算方法与算法语言[M].北京:高等教育出版社,1981.

〔3〕Philip J.Davis,Philip Rabinowitz著.冯振兴,伍富良译.张延昌校.数值积分[M].北京:高等教育出版社,1986.

〔4〕陈传璋,等.数学分析(第二版)[M].北京:高等教育出版社, 1983.

O172；O24

A

1673-260X（2017）04-0003-03

2017-01-20